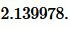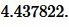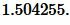Основные метрические сооьтношения в прямоугольном треугольнике
- §1. Прямоугольный треугольник. Метрические соотношения.
- Радиус вписанной окружности в прямоугольный треугольник онлайн
- 1. Радиус вписанной в прямоугольный треугольник окружности, если известны катеты треугольника
- 2. Радиус вписанной в прямоугольный треугольник окружности, если известны катет и прилегающей к нему острый угол
- 3. Радиус вписанной в прямоугольный треугольник окружности, если известны катет и противолежащий острый угол
- Нахождение радиуса описанной вокруг треугольника окружности
- Формулы вычисления радиуса описанной окружности
- Произвольный треугольник
- Прямоугольный треугольник
- Равносторонний треугольник
- Примеры задач
- 📽️ Видео
§1. Прямоугольный треугольник. Метрические соотношения.
Основные метрические сооьтношения в прямоугольном треугольнике
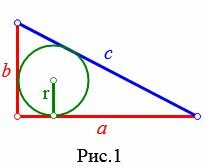
Пусть `ABC` прямоугольный треугольник с прямым углом `C` и острым углом при вершине `A`, равным `alpha` (рис. 1).
Используем обычные обозначения:
`c` — гипотенуза `AB`;
`a` и `b` – катеты `BC` и `AC` (по-гречески «kathetos — катет» означает отвес, поэтому такое изображение прямоугольного треугольника нам представляется естественным);
`a_c` и `b_c` – проекции `BD` и `AD` катетов на гипотенузу;
`h` – высота `CD`, опущенная на гипотенузу;
`m_c` – медиана `CM`, проведённая к гипотенузе;
`R` – радиус описанной окружности;
`r` – радиус вписанной окружности.
Напомним, что если `alpha` — величина острого угла `A` прямоугольного треугольника `ABC` (см. рис. 1), то
`sin alpha = a/c`, `cos alpha = b/c` и `»tg»alpha = a/b`.
Значения синуса, косинуса и тангенса острого угла прямоугольного треугольника зависят только от меры угла и не зависят от размеров и расположения треугольника.
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов:
`c^2 = a^2 + b^2`
Доказательство теоремы повторите по учебнику.
Выведем ряд соотношений между элементами прямоугольного треугольника.
Квадрат катета равен произведению гипотенузы и его проекции на гипотенузу
Если `/_ A = alpha` (см. рис. 1), то `/_ CBD = 90^@ — alpha` и `/_ BCD = alpha`. Из треугольника `ABC` `sin alpha = (BC)/(AB)`, а из треугольника `BCD` `sin alpha = (BD)/(BC)`.
Значит, `(BC)/(AB) = (BD)/(BC)`, откуда `BC^2 = AB * BD`, т. е. `a^2 = c * a_c` . Аналогично доказывается второе равенство.
Квадрат высоты, опущенной на гипотенузу, равен произведению проекции катетов на гипотенузу
Из треугольника `ACD` (рис. 1) имеем `»tg»alpha = (CD)/(AD)`, а из треугольника `BCD` `»tg»alpha = (BD)/(CD)`.
Значит `(BD)/(CD) = (CD)/(AD)`, откуда `CD^2 = AD * BD`, т. е. `h^2 = a_c * b_c`.
Произведение катетов равно произведению гипотенузы и высоты, опущенной на гипотенузу
Из треугольника `ABC` имеем `sin alpha = (BC)/(AB)`, а из треуольника `ACD` `sin alpha = (CD)/(AC)`.
Таким образом, `(BC)/(AB) = (CD)/(AC)`, откуда `BC * AC = AB * CD`, т. е. `a * b = c * h`.
Медиана, проведённая к гипотенузе, равна половине гипотенузы, т. е.
Пусть `AM = BM`. Проведём $$ MKVert BC$$ (рис. 2), тогда по теореме Фалеса `AK = CK`
.
Кроме того, из того, что `BC _|_ AC` и $$ MKVert BC$$ следует `MK _|_ AC`. В прямоугольных треугольниках `CMK` и `AMK` катет `MK` общий, катеты `CK` и `AK` равны. Эти треугольники равны и `CM = AM`, т. е. `CM = 1/2 AB`.
Полезно также запомнить, что медиана к гипотенузе разбивает треугольник на два равнобедренных треугольника.
Радиус окружности, описанной около прямоугольного треугольника, равен половине гипотенузы
Это следует из Свойства 4, действительно, `MA = MB = MC`, следовательно, окружность с центром в точке `M` и радиуса `c/2` проходит через три вершины.
Сумма катетов равна удвоенной сумме радиусов описанной и вписанной окружностей
`a + b = 2(R + r)` или `a + b = c + 2r`
Пусть `O` — центр вписанной окружности и `F`, `N` и `S` — точки касания сторон треугольника `ABC` (рис. 3), тогда `OF_|_ BC`, `ON _|_ AC`, `OS _|_ AB` и `OF = ON = OS = r`. Далее, `OFCN` — квадрат со стороной `r`, поэтому `BF = BC — FC`, `AN = AC — CN`, т. е. `BF = a — r` и `AN = b — r`.
Прямоугольные треугольники `AON` и `AOS` равны (гипотенуза `AO` — общая, катеты `ON` и `OS` равны), следовательно, `AS = AN`, т. е. `AS = b — r`.
Аналогично доказывается, что `BS = a — r`, поэтому из `AB = AS + BS` следует `c = (b — r) + (a — r)`, т. е. `a + b = c + 2r`. Зная, что `c = 2R`, окончательно получаем `a + b = 2(R + r)`.
Равенства, доказанные в Свойствах 1 и 2, записываются также как:
Видео:Геометрия Радиусы вписанной и описанной окружностей прямоугольного треугольника равны соответственноСкачать

Радиус вписанной окружности в прямоугольный треугольник онлайн
С помощю этого онлайн калькулятора можно найти радиус вписанной в любой треугольник окружности, в том числе радиус вписанной в прямоугольный треугольник окружности. Для нахождения радиуса вписанной в треугольник окружности выберите тип треугольника, введите известные данные в ячейки и нажмите на кнопку «Вычислить». Теоретическую часть и численные примеры смотрите ниже.
| Открыть онлайн калькулятор |
Видео:Вариант 72, № 7. Радиусы вписанной и описанной окружностей прямоугольного треугольника. ЗадачаСкачать

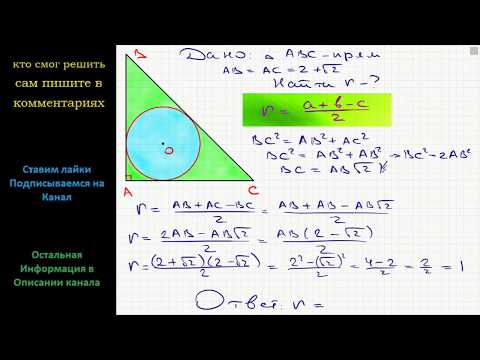
1. Радиус вписанной в прямоугольный треугольник окружности, если известны катеты треугольника
Пусть известны катеты a и b прямоугольного треугольника (Рис.1). Выведем формулу вычисления радиуса вписанной в треугольник окружности.
 |
Радиус вписанной в треугольник окружности, если известна площадь треугольника S и полупериметр p вычисляется из следующей формулы (статья Радиус вписанной в треугольник окружности, формула (5)):
| ( small r= frac, ) | (1) |
| ( small p= frac. ) | (2) |
Площадь прямоугольного треугольника по катетам вычисляется из формулы:
| ( small S= large frac small cdot a cdot b. ) | (3) |
Подставляя (2) и (3) в (1) получим формулу вписанной в прямоугольный треугольник окружности:
| ( small r= large frac<fracab><frac(a+b+c)> ) ( small = large frac, ) | (4) |
| ( small c= sqrt. ) | (5) |
Из формулы (4) выведем другую эквивалентную формулу. Умножим числитель и знаменатель формулы (4) на ( small a+b-c ):
| ( small r= frac ) ( small = frac ) ( small = frac ) | (6) |
Учитывая (5), формулу (6) можно переписать так:
| ( small r= frac ) ( small = frac .) |
Таким образом другая формула вычисления радиуса вписанной в треугольник окружности имеет вид:
| ( small r= frac ,) | (7) |
где c вычисляется из (5).
Пример 1. Известны катеты прямоугольного треугольника a=17 и b=5. Найти радиус окружности вписанной в треугольник.
Решение. Для нахождения радиуса окружности вписанной в треугольник воспользуемся одним из формул (4) и (7). Вычислим, сначала, гипотенузу прямоугольного треугольника из формулы (5):
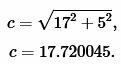 |
Подставим значения ( small a=17, ; b=5; c=17.720045 ) в (7):
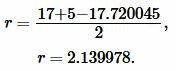 |
Ответ:
Видео:Найти радиус равнобедренного прямоугольного треугольника 3 задание проф. ЕГЭ по математикеСкачать

2. Радиус вписанной в прямоугольный треугольник окружности, если известны катет и прилегающей к нему острый угол
Пусть известны катет a прямоугольного треугольника и прилежащий к нему угол β(Рис.2). Выведем формулу радиуса вписанной в треугольник окружности.
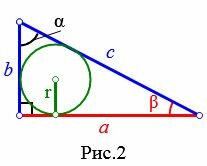 |
| ( small frac=frac .) |
Учитывая, что ( small alpha=90°-beta ) и ( small sin (90°-beta)=cos beta ), получим:
| ( small frac=frac ) ( small =frac=frac .) | (8) |
Тогда из (8) получим:
| ( small b=frac. ) | (9) |
Далее, из теоремы синусов:
| ( small frac=frac ) ( small =frac=frac .) |
| ( small c=frac .) | (10) |
Чтобы получить формулу радиуса вписанной в прямоугольный треугольник окружности через катет и прилежащий к нему угол, подставим значения ( small b ) и ( small c ) из (9) и (10) в (7):
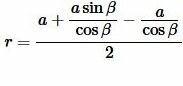 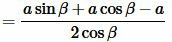 |
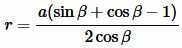 | (11) |
Пример 2. Известны катет ( small a=21 ) и прилежащий к нему угол ( small beta=30° ) прямоугольного треугольника. Найти радиус окружности вписанной в треугольник.
Решение. Для нахождения радиуса окружности вписанной в треугольник воспользуемся формулой (11). Подставим значения ( small a=21 ) ( small beta=30° ) в (11):
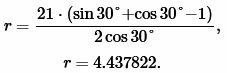 |
Ответ:
Видео:Сможешь найти радиус окружности? Окружность, вписанная в прямоугольный треугольникСкачать

3. Радиус вписанной в прямоугольный треугольник окружности, если известны катет и противолежащий острый угол
Пусть известны катет a прямоугольного треугольника и противолежащий угол ( small alpha; ) (Рис.3). Найдем формулу радиуса вписанной в треугольник окружности.
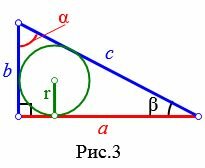 |
В предыдущем параграфе мы вывели формулу вписанной в прямоугольный треугольник окружности по катету и прилежащему углу (формула (11)). Учитывая, что в прямоугольном треугольнике сумма острых углов равна 90°, имеем:
| ( small alpha+beta=90°) ( small beta=90°-alpha ) |
Тогда (11) можно преобразовать так (подробнее на странице Формулы приведения тригонометрических функций:
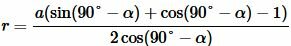 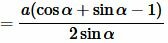 |
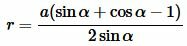 | (12) |
Пример 3. Известны катет ( small a=6 ) прямоугольного треугольника и противолежащий угол ( small alpha=53°. ) Найти радиус окружности вписанной в треугольник.
Решение. Для нахождения радиуса окружности вписанной в треугольник воспользуемся формулой (12). Подставим значение ( small a=6, ; alpha=53° ) в (12):
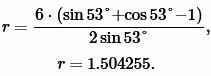 |
Ответ:
Видео:Шестнадцатое задание ОГЭ по математике (1) #огэ #огэ2023 #огэматематика #огэпоматематике #математикаСкачать

Нахождение радиуса описанной вокруг треугольника окружности
В данной публикации мы рассмотрим формулы, с помощью которых можно вычислить радиус окружности, описанной около произвольного (любого), прямоугольного или равностороннего треугольника. Также разберем примеры решения задач для закрепления представленного теоретического материала.
Видео:Геометрия Катеты равнобедренного прямоугольного треугольника равны 2+√2. Найдите радиус окружностиСкачать
Формулы вычисления радиуса описанной окружности
Произвольный треугольник
Радиус окружности, описанной вокруг любого треугольника, рассчитывается по формуле:
где a, b, c – стороны треугольника, S – его площадь.
Прямоугольный треугольник
Радиус окружности, описанной около прямоугольного треугольника, равен половине его гипотенузы или высоте, проведенной к гипотенузе.
Равносторонний треугольник
Радиус описанной около правильного треугольника окружности вычисляется по формуле:
где a – сторона треугольника.
Видео:Радиус описанной окружностиСкачать

Примеры задач
Задание 1
Дан треугольник со сторонами 4, 6 и 9 см. Найдите радиус описанной около него окружности.
Решение
Для начала нам необходимо найти площадь треугольника. Т.к. нам известны длины всех его сторон, можно применить формулу Герона:
Теперь мы можем воспользоваться первой формулой из перечисленных выше для расчета радиуса круга:
Задание 2
Дан треугольник, у которого известны две стороны из трех: 6 и 8 см. Найдите радиус описанной вокруг него окружности.
Решение
Треугольник со сторонами 6 и 8 см может быть только прямоугольным, причем известные по условиям задачи стороны являются его катетами. Таким образом, мы можем найти гипотенузу фигуры, воспользовавшись теоремой Пифагора:
Как мы знаем, радиус круга, описанного вокруг прямоугольного треугольника, равняется половине его гипотенузы, следовательно: R = 10 : 2 = 5.
📽️ Видео
Окружность вписанная в треугольник и описанная около треугольника.Скачать

Задача 6 №27932 ЕГЭ по математике. Урок 146Скачать

Радиус окружности, описанной около прямоугольного треугольника, равен 4. Найдите гипотенузу.Скачать

Геометрия 9 класс. Радиус описанной и вписанной окружности треугольника. Формулы радиуса.Скачать

№705. Около прямоугольного треугольника ABC с прямым углом С описана окружность. Найдите радиусСкачать

найти радиус окружности, описанной вокруг треугольникаСкачать

Вписанная и описанная окружность - от bezbotvyСкачать

Найти радиус вписанной и описанной окружностей равностороннего треугольника. Разные способы.Скачать

Математика за минуту: Объяснение формулы радиуса вписанной окружности в прямоугольный треугольник.Скачать

Треугольник и окружность #shortsСкачать

Вписанные и описанные окружности. Вебинар | МатематикаСкачать

Геометрия Найдите радиусы вписанной и описанной окружностей треугольника со сторонами 1) 5 см 5 смСкачать

ЗАДАНИЕ 1| ЕГЭ ПРОФИЛЬ| Радиус окружности, описанной около прямоугольного треугольника, равен 4. НайСкачать