- Ваш ответ
- решение вопроса
- Похожие вопросы
- Задания В4 из Открытого банка заданий 2011 Презентация выполнена учителем математики МОУ «СОШ6» п.Передового Ставропольского края Богдановской Валентиной. — презентация
- Похожие презентации
- Презентация на тему: » Задания В4 из Открытого банка заданий 2011 Презентация выполнена учителем математики МОУ «СОШ6» п.Передового Ставропольского края Богдановской Валентиной.» — Транскрипт:
- Окружность, вписанная в четырехугольник
- 🌟 Видео
Видео:ЕГЭ Математика Задание 6#27952Скачать
Ваш ответ
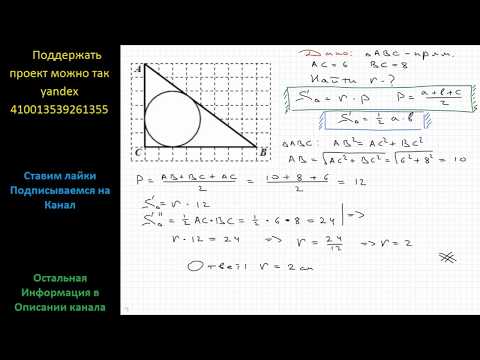
Видео:Геометрия Найдите радиус окружности, вписанной в треугольник АВС, если размер клетки 1 см х 1 смСкачать
решение вопроса
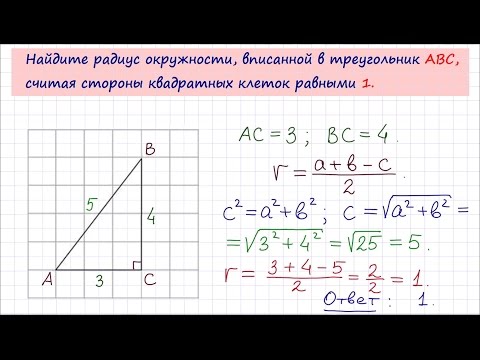
Видео:Задача 6 №27951 ЕГЭ по математике. Урок 149Скачать
Похожие вопросы
- Все категории
- экономические 43,277
- гуманитарные 33,618
- юридические 17,900
- школьный раздел 606,754
- разное 16,824
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
Видео:Задача 6 №27913 ЕГЭ по математике. Урок 131Скачать

Задания В4 из Открытого банка заданий 2011 Презентация выполнена учителем математики МОУ «СОШ6» п.Передового Ставропольского края Богдановской Валентиной. — презентация
Презентация была опубликована 7 лет назад пользователемЮлия Шишкина
Похожие презентации
Видео:Урок 2. Описанная окружность около четырехугольника. Задача из ОГЭ| Подобные треугольникиСкачать

Презентация на тему: » Задания В4 из Открытого банка заданий 2011 Презентация выполнена учителем математики МОУ «СОШ6» п.Передового Ставропольского края Богдановской Валентиной.» — Транскрипт:
1 Задания В4 из Открытого банка заданий 2011 Презентация выполнена учителем математики МОУ «СОШ6» п.Передового Ставропольского края Богдановской Валентиной Михайловной 2011
2 Около окружности, радиус которой равен 8, описан квадрат. Найдите радиус окружности, описанной около этого квадрата. 8 АВ = 28 = а Т.к. R = a /2 R = AC/2, АС можно найти из АСВ по теореме Пифагора, зная стороны квадрата Ответ:
3 Ответ: Найдите радиус окружности, описанной около прямоугольного треугольника ABC, если стороны квадратных клеток равны 1. Т.к. центр окружности, описанной около прямоугольного треугольника лежит на середине гипотенузы, а ее длина равна 5, то R = 2,5 2,
4 Найдите радиус окружности, вписанной в квадрат ABCD, считая стороны квадратных клеток равными 2. r = ОМ, т.к. ОМ перпендикуляр к CD Ответ: О М К Из ОМК найдем гипотенузу ОМ по теореме Пифагора ОМ = 2 = r
5 Найдите радиус окружности, описанной около правильного треугольника ABC, считая стороны квадратных клеток равными 1. К Треугольник АВС равнобедренный. ВК – медиана и высота. Т.к. О- центр окружности является точкой пересечения медиан, то R = 2 Ответ:
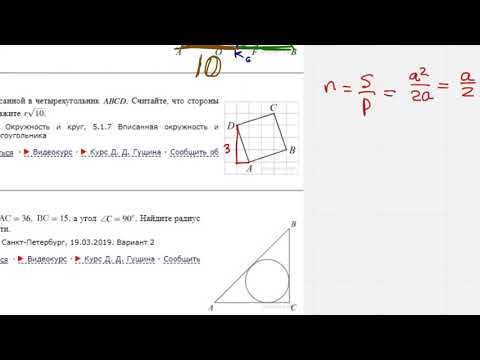
6 Найдите радиус r окружности, вписанной в четырехугольник ABCD. В ответе укажите r10. АВ найдем из треугольника АВК по т. Пифагора. АВ = 10 r = 0,5 10 К Ответ:
7 В четырехугольник ABCD вписана окружность, АВ=10, CD=16. Найдите периметр четырехугольника. В любом описанном четырехугольнике суммы противоположных сторон равны. AB+CD= 26 P = 26*2 = 52 Ответ:
8 К окружности, вписанной в треугольник ABC, проведены три касательные. Периметры отсеченных треугольников равны 6, 8, 10. Найдите периметр данного треугольника M N O K Т.к. OM и ON –радиусы, проведенные в точку касания, то ˂MNO = ˂OKM = 90°, значит треугольники MNO и MKO равны по катету и гипотенузе, MK=MN, так же KP = PS, значит MP = MN+PS. Аналогично для треугольников с периметрами 10 и 8. Т.о. периметр данного треугольника равен сумме исходных периметров, т.е. 24 P R S Ответ: 2 4
9 Боковые стороны равнобедренного треугольника равны 5, основание равно 6. Найдите радиус вписанной окружности. К СК – медиана, биссектриса, высота треугольника. Из АСК по т.Пифагора найдем высоту СК. СК = 4, S = ½*AB*CK = 12, P = 16, r = 2S:P = 24:16 = 1, Ответ: 1, 5 S = Pr:2
10 Боковые стороны трапеции, описанной около окружности, равны 3 и 5. Найдите среднюю линию трапеции. В любом описанном четырехугольнике суммы противоположных сторон равны. DC+AB = 8 Таким образом MN = 4 MN Пусть MN – средняя линия трапеции, МN = ½(DC+AB) АD+CB = 8 Ответ:
11 Периметр правильного шестиугольника равен 72. Найдите диаметр описанной окружности. P = 72, значит a = 12, т.к. R = a = 12 D = 2R = 24 Ответ: 2 4 a R 27929
12 Угол между стороной правильного n-угольника, вписанного в окружность, и радиусом этой окружности, проведенным в одну из вершин стороны, равен 54°. Найдите n А В С ˂ А = 180° — 54°*2 = 72° АВ = АС = R ABC равнобедренный n = 360° : 72° = 5 Ответ: 5
13 Радиус окружности, вписанной в равнобедренный прямоугольный треугольник, равен 2. Найдите гипотенузу c этого треугольника. В ответе укажите. К Ответ: СК – медиана биссектриса, высота равнобедренного треугольника АВС. ОК = ОР = ОМ = r = 2 О М Р АС – касательная, СК — секущаяСР² = СН*СК, т.к. СН = СК-4, то 2² = (СК-4)*СК, СК = 2(1+2) Н Т.к. треугольник АКС равнобедренный (˂КАС = ˂АСК=45°), то КС = АК АВ = 2АК = 4 (1+2) 4
14 Около трапеции описана окружность. Периметр трапеции равен 22, средняя линия равна 5. Найдите боковую сторону трапеции Т.к., то DC+AB = 10 AD + CB = P – 10 = 12 Т.к. в любом вписанном четырехугольнике сумма противоположных углов равна 180°, то ABCD – равнобедренная трапеция. AD = 6 Ответ: 6
15 Боковая сторона равнобедренной трапеции равна ее меньшему основанию, угол при основании равен 60°, большее основание равно 12. Найдите радиус описанной окружности этой трапеции. 60° 12 MN Ответ: ˂BCN= 30° Обозначив СВ = х и, учитывая свойство катета, лежащего напротив угла 30°, составим и решим уравнение: х+0,5 х+0.5 х = 12, х = 6. О Т.к. OM = OD = OC = OB =6. R = 6 6
16 Два угла вписанного в окружность четырехугольника равны 82° и 58°. Найдите больший из оставшихся углов. Ответ дайте в градусах В любом вписанном четырехугольнике сумма противоположных углов равна 180°, значит углы 82° и 58° соседние (А и В). ˂В= 58°, значит ˂D=180°-58°=122° Ответ: ° 58°
17 Углы A,B и C четырехугольника ABCD относятся как 1:2:3. Найдите угол D, если около данного четырехугольника можно описать окружность. Ответ дайте в градусах A B C D В любом вписанном четырехугольнике сумма противоположных углов равна 180°, значит ˂А + ˂С = 180°, таким образом ˂А =180° : (1+3) = 45° ˂В = 2*45° = 90° Ответ: ˂D = 90° 9 0
18 Одна сторона треугольника равна радиусу описанной окружности. Найдите угол треугольника, противолежащий этой стороне. Ответ дайте в градусах Ответ: D По условию задачи треугольник АВD равносторонний, Т.к ˂ADB – центральный, а ˂АСВ – вписанный, но опирающийся на ту же дугу, то его величина составляет 30° 3 0 ˂ADB = 60°
19 Сторона AB треугольника ABC равна 1. Противолежащий ей угол C равен 150°. Найдите радиус окружности, описанной около этого треугольника Ответ: О ˂ACB – вписанный, значит дуга на которую он опирается равна 300° Величина дуги АСВ, а значит и центрального ˂АОВ = 60°, а т.к. АО = ОВ = R, то треугольник АОВ равносторонний, R = 1` 1
20 Сторона AB тупоугольного треугольника ABC равна радиусу описанной около него окружности. Найдите угол C. Ответ дайте в градусах Ответ: O Т.к. АО = ОВ = АВ, то треугольник АОВ равносторонний, значит ˂ АОВ = 60° Величина дуги АСВ равна 60°, величина оставшейся дуги 360° — 60° =300°, Вписанный ˂С равен половине дуги, на которую он опирается, т.е. ˂С =150° 1 5 0
21 Три стороны описанного около окружности четырехугольника относятся (в последовательном порядке) как 1:2:3. Найдите большую сторону этого четырехугольника, если известно, что его периметр равен 32. Ответ: В любом описанном четырехугольнике суммы противоположных сторон равны, значит AD+CB = DC+AB,т.е. х+3 х = 32-4 х х = 4 DC = 32- AB-AD-BC = = 8 8
22 Найдите радиус R окружности, описанной около треугольника ABC, если стороны квадратных клеток равны 1. В ответе укажите R CB = 20 (используя т.Пифагора). Центр окружности, описанной около прямоугольного треугольника, лежит в середине гипотенузы, значит R =CB:2, R = 25/2 = 5 Ответ:
Видео:2041 четырёхугольник ABCD вписан в окружность угол abd равен 38 угол cаd равен 54 Найдите угол ABCСкачать

Окружность, вписанная в четырехугольник
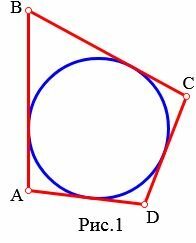
Определение 1. Окружность называют вписанным в четырехугольник, если окружность касается всех сторон четырехугольника.
На рисунке 1 окружность вписан в четырехугольник ABCD. В этом случае говорят также, что четырехугольник описан около окружности.
 |
Теорема 1. Если окружность вписан в четырехугольник, то сумма противолежащих сторон четырехугольника равны.
Доказательство. Пусть окружность ABCD вписан в четырехугольник (Рис.2). Докажем, что ( small AB+CD=AD+BC ).
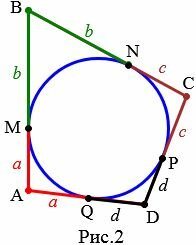 |
Точки M, N, Q, P − точки касания окружности со сторонами четырехугольника. Так как отрезки касательных, проведенных к окружности через одну точку, равны (статья Касательная к окружности теорема 2), то
| ( small AM=AQ=a, ) ( small BM=BN=b, ) ( small CN=CP=c, ) ( small DQ=DP=d ) |
| ( small AB+CD ) ( small=AM+BM+CP+DP ) ( small =a+b+c+d, ) | (1) |
| ( small AD+BC) ( small=AQ+DQ+BN+CN) ( small=a+d+b+c. ) | (2) |
Из равенств (1) и (2), следует:
( small AB+CD=AD+BC. )  |
Теорема 2. Если в выпуклом четырехугольнике сумма противолежащих сторон равны, то в него можно вписать окружность.
Доказательство. Пусть задан выпуклый четырехугольник ABCD и пусть ( small AB+CD=AD+BC. ) (Рис.3). Докажем, что в него можно вписать окружность.
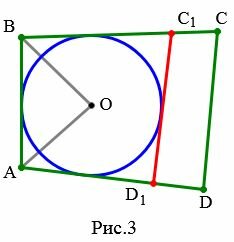 |
Проведем биссектрисы углов A и B четырехугольника ABCD. Точку их пересечения обозначим буквой O. Тогда точка O равноудалена от сторон AB, BC, AD. Следовательно существует окружность с центром в точке O, которая касается этих трех сторон.
Пусть эта окружность не касается стороны CD. Тогда возможны два случая.
Случай 1. Сторона CD не имеет общих точек с построенной окружностью.
Проведем касательную C1D1 к окружности, параллельно стороне CD четырехугольника.
Тогда окружность с центром O вписан в четырехугольник ABC1D1. Следовательно, по теореме 1, имеем:
| ( small AB+C_1D_1=AD_1+BC_1. ) | (3) |
Но по условию данной теоремы:
| ( small AB+CD=AD+BC. ) | (4) |
Вычтем из равенства (4) равенство (3):
| ( small CD-C_1D_1) (small=AD-AD_1+BC-BC_1 ) |
| ( small CD-C_1D_1=DD_1+CC_1 ) |
| ( small CD=DD_1+CC_1+C_1D_1) |
Получили, что в четырехугольнике CC1D1D длина одной стороны равна сумме длин трех остальных сторон, что невозможно (см. задачу 1 статьи Четырехугольник).
Таким образом сторона CD должна иметь общие точки с рассматриваемой окружностью.
Случай 2. Сторона CD имеет две общие точки с построенной окружностью (Рис.4).
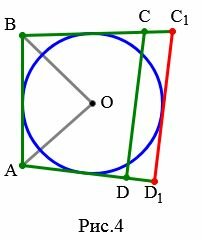 |
Аналогичными рассуждениями можно показать, что сторона CD не может иметь две общие точки с построенной окружностью.
Следовательно, предполагая, что построенная окружность не касается стороны CD, мы пришли к противоречию. Таким образом, если в выпуклом четырехугольнике сумма противолежащих сторон равны, то в него можно вписать окружность.
Если в четырехугольник вписан окружность, то существует точка, равноудаленная от всех сторон четырехугольника. Эта точка является центром вписанной в четырехугольник окружности. Для нахождения этой точки достаточно найти точку пересечениия биссектрис двух соседних углов данного четырехугольника.
🌟 Видео
3 правила для вписанного четырехугольника #shortsСкачать

Задача 6 №27932 ЕГЭ по математике. Урок 146Скачать

Найти радиус равнобедренного прямоугольного треугольника 3 задание проф. ЕГЭ по математикеСкачать

Четырёхугольник ABCD вписан в окружность ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать

16) Четырехугольник АВСD описан около окружности, AD=7, DC=12, BC=13. Найдите AB. Математика огэ.Скачать

ОПИСАННЫЕ И ВПИСАННЫЕ ОКРУЖНОСТИ ЧЕТЫРЕХУГОЛЬНИКА . §10 геометрия 8 классСкачать

ТЕСТ НА ЭРУДИЦИЮ и кругозор: МНОГО УМНЫХ ВОПРОСОВ, ответы знает не каждый. #насколькотыумный #тестСкачать

8 класс Геометрия. Окружность вписанная в четырехугольник и описанная около четырехугольника Урок #4Скачать

Задача 6 №27934 ЕГЭ по математике. Урок 148Скачать

ОГЭ по математике. Окружность - ваш гарантированный +1 баллСкачать

11 класс, 44 урок, Описанный четырехугольникСкачать

Задача 6 №27910 ЕГЭ по математике. Урок 130Скачать

Четырехугольники, вписанные в окружность. 9 класс.Скачать

Задача 6 №27909 ЕГЭ по математике. Урок 129Скачать
