Найдите площадь треугольника вписанного в окружность с радиусом 4

Зависит от того, какой треугольник.

Чтобы найти площадь треугольника, надо сначала определить тип треугольника: прямоугольный, равнобедренный, равносторонний. Если он у вас не такой – отталкивайтесь от других данных: высоты, вписанной или описанной окружности, длин сторон. Привожу все формулы ниже.

Видео:Задача 6 №27624 ЕГЭ по математике. Урок 71Скачать

Если треугольник прямоугольный

То есть один из его углов равен 90 градусам.

Надо перемножить катеты и поделить на два. Катеты – это две меньшие стороны, в сравнении с гипотенузой. Гипотенуза – это самая длинная сторона, она всегда находится напротив угла в 90 градусов.

Видео:Задание 24 Площадь описанного треугольникаСкачать

Если он равнобедренный

То есть у него равны боковые стороны. В таком случае надо провести высоту к основанию (той стороне, которая не равна «бедрам»), перемножить высоту с основанием и поделить результат на два.

Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

Если он равносторонний

То есть все три стороны равны. Ваши действия такие:

1. Найдите квадрат стороны – умножьте эту сторону на нее же. Если у вас сторона равна 4, умножьте 4 на 4, будет 16.
2. Умножьте полученное значение на корень из 3. Это примерно 1,732050807568877293527.
3. Поделите все на 4.

Видео:Вписанная и описанная окружность - от bezbotvyСкачать

Если известна сторона и высота

Площадь любого треугольника равна половине произведения стороны на высоту, которая к этой стороне проведена. Именно к этой, а не к какой-то другой.

Чтобы провести высоту к стороне, надо найти вершину (угол), которая противоположна этой стороне, а потом опустить из нее на сторону прямую линию под углом в 90 градусов. На картинке высота обозначена синим цветом и буквой h, а линия, на которую она опускается, красным цветом и буквой a.

Видео:Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

Если известны две стороны и градус угла между ними

Если вы знаете, чему равны две стороны и угол между ними, то надо найти синус этого угла, умножить его на первую сторону, умножить на вторую и еще умножить на ½:

Видео:Вписанные и описанные окружности. Вебинар | МатематикаСкачать

Если известны длины трех сторон

1. Найдите периметр. Для этого сложите все три стороны.
2. Найдите полупериметр – разделите периметр на два. Запомните значение.
3. Отнимите от полупериметра длину первой стороны. Запомните.
4. Отнимите от полупериметра длину второй стороны. Тоже запомните.
5. Отнимите от полупериметра длину третьей стороны. И ее запомните.
6. Умножьте полупериметр на каждое из этих чисел (разницу с первой, второй и третьей стороной).
7. Найдите квадратный корень.

Эта формула еще называется формулой Герона. Возьмите на заметку, если вдруг учитель спросит.

Видео:Задание 16 ОГЭ по математике. Две окружности одна описана около квадрата, другая вписана в него.Скачать

Если известны три стороны и радиус описанной окружности

Окружность вы можете описать вокруг любого треугольника. Чтобы найти площадь «вписанного» треугольника – того, который «вписался» в окружность, надо перемножить три его стороны и поделить их на четыре радиуса. Смотрите картинку.

Видео:Найдите площадь треугольника на рисунке ★ Два способа решенияСкачать

Если известны три стороны и радиус вписанной окружности

Если вам удалось вписать в треугольник окружность, значит она обязательно касается каждой из его сторон. Следовательно, расстояние от центра окружности до каждой из сторон треугольника – ее радиус.

Чтобы найти площадь, посчитайте сначала полупериметр – сложите все стороны и поделите на два. А потом умножьте его на радиус.

Это были все способы найти площадь треугольника. Спасибо, что дочитали статью до конца. Лайкните, если не трудно.

Видео:Окружность || Часть 4 || Треугольник, вписанный в окружностьСкачать

Найти площадь равностороннего треугольника вписанного в окружность радиуса 4√3 см?

Геометрия | 5 — 9 классы

Найти площадь равностороннего треугольника вписанного в окружность радиуса 4√3 см.

R правильного = $asqrt:3$

площадь = $sqrt:4 * а^2$.

Видео:Только 1 может решить эту хитрую задачу ★ Найдите углы треугольника ★ Супер ЖЕСТЬСкачать

В равностороннем треугольнике вписана окружность радиусом 8 см?

В равностороннем треугольнике вписана окружность радиусом 8 см.

Найти сторону треугольника.

Видео:Длина окружности. Площадь круга. 6 класс.Скачать

Периметр равностороннего треугольника равен 12?

Периметр равностороннего треугольника равен 12.

Найти радиус окружности вписанной в треугольник.

Видео:№471. Найдите площадь прямоугольного треугольника, если его катеты равны: а) 4 см и 11см;Скачать

В равносторонний треугольник вписанный окружности радиусом 8 см?

В равносторонний треугольник вписанный окружности радиусом 8 см.

Найти сторону треугольника.

Видео:Площадь треугольника. Как найти площадь треугольника?Скачать

Равносторонний треугольник ABC вписан в окружность радиуса 6 см найти сторону треугольника?

Равносторонний треугольник ABC вписан в окружность радиуса 6 см найти сторону треугольника.

Видео:Задание 24 Площадь вписанного равнобедренного треугольникаСкачать

Треугольник АВС равносторонний?

Треугольник АВС равносторонний.

Строна АВ = 6 см.

Найти : высоту, площадь, радиус вписанной окружности и радиус описанной окружности.

Видео:Окружность вписана в равнобедренный треугольник. Найти её радиус.Скачать

Радиус окружности, вписанной в равносторонний треугольник, равен см?

Радиус окружности, вписанной в равносторонний треугольник, равен см.

Найти сторону треугольника.

Видео:Геометрия 9 класс. Радиус описанной и вписанной окружности треугольника. Формулы радиуса.Скачать

1. Докажите, что в равностороннем треугольнике радиус описанной окружности в 2 раза больше радиуса вписанной окружности?

1. Докажите, что в равностороннем треугольнике радиус описанной окружности в 2 раза больше радиуса вписанной окружности.

2. Площадь равностороннего треугольника равна 48.

Найти радиус описанной около этого треугольника окружности.

Видео:Задание 16 ОГЭ по математике. Самая сложная задача. Окружность вписана в произвольный треугольник.Скачать

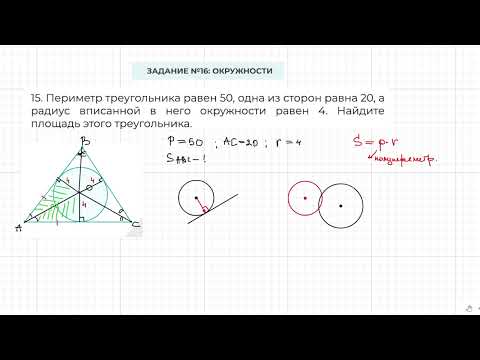
В равносторонний треугольник вписана окружность?

В равносторонний треугольник вписана окружность.

Длина стороны треугольника 2 корня из 3.

Нужно найти радиус вписанной окружности.

Видео:№693. В прямоугольный треугольник вписана окружность радиуса r. Найдите периметр треугольника,Скачать

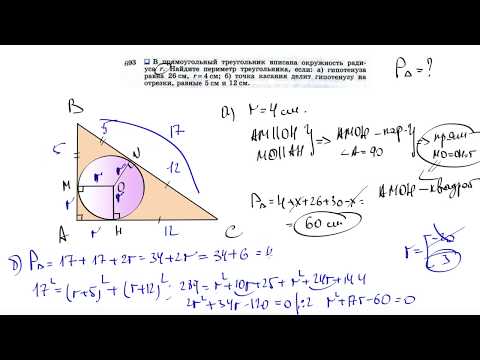
Равносторонний треугольник вписан в окружность с радиусом 6 см?

Равносторонний треугольник вписан в окружность с радиусом 6 см.

Видео:Формулы равностороннего треугольника #shortsСкачать

Как найти периметр равностороннего треугольника вписанного в окружность, если радиус = 10 см?

Как найти периметр равностороннего треугольника вписанного в окружность, если радиус = 10 см.

Вы зашли на страницу вопроса Найти площадь равностороннего треугольника вписанного в окружность радиуса 4√3 см?, который относится к категории Геометрия. По уровню сложности вопрос соответствует учебной программе для учащихся 5 — 9 классов. В этой же категории вы найдете ответ и на другие, похожие вопросы по теме, найти который можно с помощью автоматической системы «умный поиск». Интересную информацию можно найти в комментариях-ответах пользователей, с которыми есть обратная связь для обсуждения темы. Если предложенные варианты ответов не удовлетворяют, создайте свой вариант запроса в верхней строке.

Мама за 30 минут прошла 2, 5 км, Юра проехал 6 км. Имеем прямоугольный треугольник с катетами 2, 5 и 6 км. Надо найти гипотенузу. С² = 2, 5² + 6² = 6, 25 + 36 = 72, 25 с = √72, 25 = 8, 5 Ответ : 8, 5 км.

Вот 180 — (65 + 50) = 65 и т. Д На фото.

По — моему, есть ошибка в вопросе.

Пусть х — один из смежных углов, тогда второй угол 180 — х. Биссектриса первого угла — х / 2, второго — (180 — х) / 2 = 90 — (x / 2). Т. к. Биссектрисы выходят из одной точки то угол между ними равен (х / 2) + 90 — (х — 2) = 90. Следовательно, би..

126 градусов, 76 + 50 = 126.

АОВ + ВОР = 76 + 50 = 126 поплидмзмшь.

Розв»язок додала. Вiдповiдь 112см².

10 : 2 = 5 25 : 2 = 12, 5 5 ^ 2 + 12, 5 ^ 2 = 13, 462 ^ 2 13, 462 * 4 = 53, 848.

260 ответ там формула такая.

Какой вопрос? Как ответить если нет вопроса.

Видео:НАЙДИТЕ ПЛОЩАДЬ ТРЕУГОЛЬНИКАСкачать

Как найти площадь треугольника

О чем эта статья:

8 класс, 9 класс

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Основные понятия

Треугольник — это геометрическая фигура, которая получилась из трех отрезков. Их соединили тремя точками, не лежащими на одной прямой. Отрезки принято называть сторонами, а точки — вершинами.

Площадь — это численная характеристика, которая дает нам информацию о размере части плоскости, ограниченной замкнутой геометрической фигурой.

Если значения заданы в разных единицах измерения длины, мы не сможем узнать, какая площадь треугольника получится. Поэтому для правильного решения необходимо перевести все данные к одной единице измерения.

Популярные единицы измерения площади:

• квадратный миллиметр (мм 2 );
• квадратный сантиметр (см 2 );
• квадратный дециметр (дм 2 );
• квадратный метр (м 2 );
• квадратный километр (км 2 );
• гектар (га).

Формула площади треугольника

Для решения задач применяются различные формулы, в зависимости от известных исходных данных. Далее мы рассмотрим способы решения для всех типов треугольников, в том числе частные случаи для равносторонних, равнобедренных и прямоугольных фигур.

Быстро вычислить площадь треугольника поможет наш онлайн-калькулятор. Просто введите известные вам значения и получите ответ в метрах, сантиметрах или миллиметрах.

Научиться быстро щелкать задачки на нахождение площади треугольника помогут курсы по математике от Skysmart!

Общая формула

1. Площадь треугольника через основание и высоту

, где — основание, — высота.

2. Площадь треугольника через две стороны и угол между ними

, где , — стороны, — угол между ними.

3. Площадь треугольника через описанную окружность и стороны

, где , , — стороны, — радиус описанной окружности.

4. Площадь треугольника через вписанную окружность и стороны

, где , , — стороны, — радиус вписанной окружности.

Если учитывать, что — это способ поиска полупериметра, то формулу можно записать следующим образом:

5. Площадь треугольника по стороне и двум прилежащим углам

, где — сторона, и — прилежащие углы.

6. Формула Герона для вычисления площади треугольника

Сначала необходимо подсчитать разность полупериметра и каждой его стороны. Потом найти произведение полученных чисел, умножить результат на полупериметр и найти корень из полученного числа.

, где , , — стороны, — полупериметр, который можно найти по формуле:

Для прямоугольного треугольника

Площадь треугольника с углом 90° по двум сторонам

Площадь треугольника по гипотенузе и острому углу

, где — гипотенуза, — любой из прилегающих острых углов.

Гипотенузой принято называть сторону, которая лежит напротив прямого угла.

Площадь прямоугольного треугольника по катету и прилежащему углу

, где — катет, — прилежащий угол.

Катетом принято называть одну из двух сторон, образующих прямой угол.

Площадь треугольника через гипотенузу и радиус вписанной окружности

, где — гипотенуза, — радиус вписанной окружности.

Площадь треугольника по отрезкам, на которые делит вписанная окружность его гипотенузу

, где , — части гипотенузы.

Площадь прямоугольного треугольника по формуле Герона

, где , — катеты, — полупериметр, который можно найти по формуле:

Для равнобедренного треугольника

Вычисление площади через основание и высоту

, где — основание, — высота, проведенная к основанию.

Поиск площади через боковые стороны и угол между ними

, где — боковая сторона, — угол между боковыми сторонами.

Площадь равностороннего треугольника через радиус описанной окружности

, где — радиус описанной окружности.

Площадь равностороннего треугольника через радиус вписанной окружности

, где — радиус вписанной окружности.

Площадь равностороннего треугольника через сторону

Площадь равностороннего треугольника через высоту

Таблица формул нахождения площади треугольника

У каждой геометрической фигуры много формул — запомнить все сразу бывает действительно сложно. В этом деле поможет регулярное решение задач и частый просмотр формул. Можно распечатать эту таблицу, использовать как закладку в тетрадке или учебнике и обращаться к ней по необходимости.