Окружность — это геометрическое место точек плоскости, равноудаленных от некоторой заданной точки (центра окружности). Расстояние между любой точкой окружности и ее центром называется радиусом окружности (радиус обозначают буквой R).
Значит, окружность — это линия на плоскости, каждая точка которой расположена на одинаковом расстоянии от центра окружности.
Кругом называется часть плоскости, ограниченная окружностью и включающая ее центр.
Отрезок, соединяющий две точки окружности, называется хордой. Хорда, проходящая через центр окружности, представляет собой диаметр. Диаметр окружности равен ее удвоенному радиусу: D = 2R.
Точка пересечения двух хорд делит каждую хорду на отрезки, произведение которых одинаково: a1a2 = b1b2
Касательная к окружности всегда перпендикулярна радиусу, проведенному в точку касания.
Отрезки касательных к окружности, проведенные из одной точки, равны: AB = AC, центр окружности лежит на биссектрисе угла BAC.
Квадрат касательной равен произведению секущей на ее внешнюю часть
Центральный угол — это угол, вершина которого совпадает с центром окружности.
Дугой называется часть окружности, заключенная между двумя точками.
Мерой дуги (в градусах или радианах) является центральный угол, опирающийся на данную дугу.
Вписанный угол это угол, вершина которого лежит на окружности, а cтороны угла пересекают ее.
Вписанный угол равен половине центрального, если оба угла опираются на одну и ту же дугу окружности.
Внутренние углы, опирающиеся на одну и ту же дугу, равны.
Сектором круга называется геометрическая фигура, ограниченная двумя радиусами и дугой, на которую опираются данные радиусы.
Периметр сектора: P = s + 2R.
Площадь сектора: S = Rs/2 = ПR 2 а/360°.
Сегментом круга называется геометрическая фигура, ограниченная хордой и стягиваемой ею дугой.
Видео:Как искать точки на тригонометрической окружности.Скачать

Точка внутри и вне окружности
Этот видеоурок доступен по абонементу
У вас уже есть абонемент? Войти
На этом занятии мы изучим тему «Точка внутри и вне окружности». На этом итоговом уроке мы повторим понятие окружности, вспомним ее основные свойства. Рассмотрим примеры расположения точки внутри и вне окружности. Вместе с преподавателем решим несколько задач на эту тему.
Видео:Точки на числовой окружностиСкачать

Окружность. Форма и положение.
Окружность — это замкнутая плоская линия, всякая точки которой равноудалена от одной и той же точки (O), называемой центром.
Прямые (OA, OB, OС. . . ), соединяющие центр с точками окружности — это радиусы.
Бесконечная прямая (MN), прочерченная через какие-нибудь две точки окружности – секущая. а часть ее (EF), заключенная между этими точками, называется хордой.
Всякая хорда (AD), прочерченная через центр — диаметр.
Диаметр представляет наибольшую из хорд..Всякий диаметр делит окружность и круг пополам. Таким образом, всякий диаметр разделит окружность на две полуокружности, а круг на два полукруга.
Какая-нибудь часть окружности (напр. EmF ) называется дугой.
О хорде (EF), соединяющей концы дуги, говорят, что она стягивает эту дугу.
Для определения дуги иногда применяют знак È ; напр., пишут так: ÈEmF.
Часть плоскости, ограниченная окружностью, именуют кругом.
Часть круга (напр., СOB, заштрихованная на чертеже), ограниченная дугой и двумя радиусами, проведенными к концам дуги, обозначают как сектор.
Часть круга, (напр., EmF), ограниченная дугой и стягивающей ее хордой, обозначают как сегмент.
Из этого получаем:
1. Все радиусы одной окружности равны.
2. Два круга с одинаковыми радиусами будут равны.
3. Диаметр равен двум радиусам.
4. Точка, лежащая внутри круга, ближе к центру, а точка, лежащая вне круга, дальше от центра, чем точки окружности.
5. Диаметр, перпендикулярный к хорде, делит эту хорду и обе стягиваемые ею дуги пополам.
6. Дуги, заключенные между параллельными хордами, равны.
При работе с окружностями применяют следующие теоремы:
1. Теорема. Прямая и окружность не могут иметь более двух общих точек.
Из этой теоремы получаем два логично вытекающих следствия:
Никакая часть окружности не может совместиться с прямой, потому что в противном случае окружность с прямой имела бы более двух общих точек.
Линия, никакая часть которой не может совместиться с прямой, называется кривой.
Из предыдущего следует, что окружность есть кривая линия.
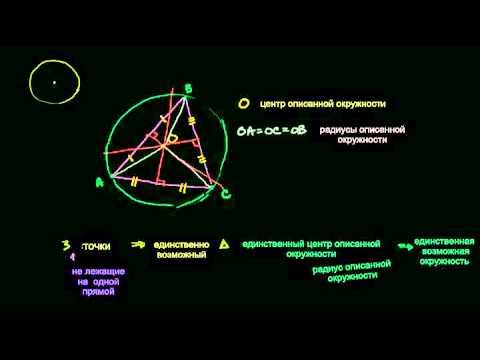
2. Теорема. Через всякие три точки, не лежащие на одной прямой, можно провести окружность и только одну.
Как следствие данной теоремы получаем:
Три перпендикуляра к сторонам треугольника вписанного в окружность проведенные через их середины, пересекаются в одной точке, которая является центром окружности.
Решим задачу. Требуется найти центр предложенной окружности.
Отметим на предложенной три любые точки A, B и С , начертим через них две хорды, например, AB и СB, и из середины этих хорд укажем перпендикуляры MN и PQ. Искомый центр, будучи одинаково удален от A, B и С, должен лежать и на MN, и на PQ, следовательно, он находится на пересечении этих перпендикуляров, т.е. в точке O.
🎦 Видео
10 класс, 11 урок, Числовая окружностьСкачать

2023 На окружности с центром в точке О отмечены точки А и Б так что угол аоб равен 45Скачать

#207. Окружность девяти точек | лемма о трезубце | ортотреугольник | прямая ЭйлераСкачать

ТРИГОНОМЕТРИЯ С НУЛЯ - Единичная Окружность // Подготовка к ЕГЭ по МатематикеСкачать

Тригонометрическая окружность. Как выучить?Скачать

Всё про углы в окружности. Геометрия | МатематикаСкачать

9 класс, 6 урок, Уравнение окружностиСкачать

Отрезки касательных из одной точки до точек касания окружности равны | Окружность | ГеометрияСкачать

№8. Верно ли утверждение: а) если две точки окружности лежат в плоскостиСкачать

Радиус и диаметрСкачать

Алгебра 10 класс. 20 сентября. Числовая окружность #6 координаты точекСкачать

Движение материальной точки по окружности | Физика ЕГЭ, ЦТСкачать

Уравнение окружности (1)Скачать

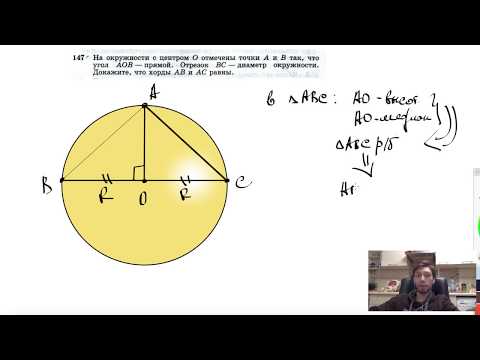
№147. На окружности с центром О отмечены точки А и В так, что угол АОВ — прямой. Отрезок ВССкачать
Четыре точки на окружности | ЕГЭ-2017. Задание 16. Математика. Профильный уровень| Борис ТрушинСкачать

Три точки, задающие окружностьСкачать
Физика 10 класс (Урок№4 - Равномерное движение точки по окружности.)Скачать

Длина окружности. Математика 6 класс.Скачать











