Найдите площадь круга описанного около четырехугольника

На данной странице калькулятор поможет рассчитать площадь четырехугольника онлайн. Для расчета задайте длину сторон, длины диагоналей и угол между ними, противолежащие углы, радиус окружности.

Четырёхугольник — многоугольник, состоящий из четырех точек (вершин) и четырёх отрезков (сторон), попарно соединяющих эти точки.

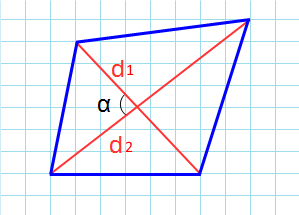
Через диагонали и угол между ними

Формула для нахождения площади четырехугольников через диагонали и угол между ними:

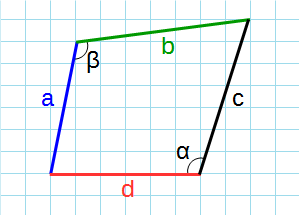
Через стороны и противолежащие углы

Формула для нахождения площади четырехугольников через стороны и противолежащие углы:

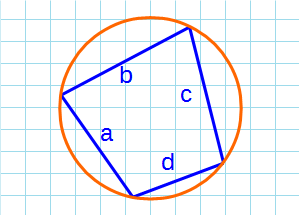
Площадь вписанного четырехугольника в окружность

Формула Брахмагупты для нахождения площади вписанного четырехугольника в окружность:

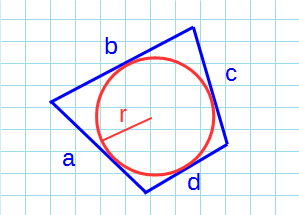
Площадь описанного четырехугольника около окружности через радиус

Формула для нахождения площади описанного четырехугольника около окружности через радиус:

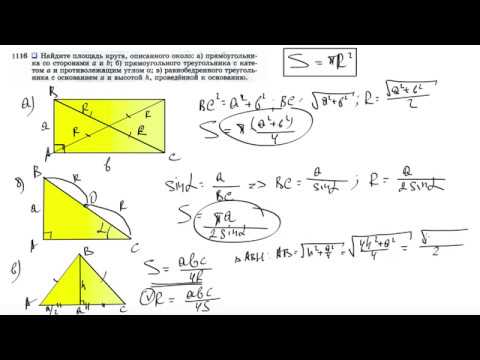
Как найти площадь круга

Площадь круга описанного около произвольного треугольника

Данная формула применима только, если вокруг треугольника можно описать круг, то есть все три вершины треугольника должны лежать на линии окружности. Треугольник в данном случае может быть любым.

Для вычисления площади круга, предварительно рассчитаем полупериметр треугольника

… подготовка … a — сторона b — сторона c — сторона 7

Видео

Найти площадь кругаОнлайн калькулятор

Радиус круга r

Диаметр – это удвоенный радиус, следовательно, подставляя его в формулу вместо последнего, нужно разделить его обратно на два.Длина окружности представляет собой удвоенное произведение радиуса и числа π: P=2πr, обратным методом получаем, что радиус равен длине окружности, разделенной на его множитель.

Формулы площади квадрата

Формула площади квадрата по длине стороны Площадь квадрата равна квадрату длины его стороны. S = a2 , где S — площадь квадрата, a — длина стороны квадрата. Формула площади квадрата по длине диагонали Площадь квадрата равна половине квадрата длины его диагонали. S = d22 , где S — площадь квадрата, d — длина диагонали квадрата.

Длина окружности круга

Множество точек удаленных от центра круга на расстояние, не превышающее радиус круга, называется кругом. Отношение длины любой окружности C к ее диаметру d всегда будет равно одному и тому же числу. Это число – всем известное число π («пи»), которое примерно равно 3,14. Так же, справедлива формула определения числа π , как отношение длины окружности C к двум ее радиусам r . Исходя из этого, выводится формула длины окружности C , которая равна произведения числа π и диаметра d окружности или 2-м ее радиусам r .

Для примера решим простую задачу, где нужно найти длину окружности, у которой известен радиус r =2 см.

Подставляем известные данные в формулу длины окружности и получаем, что длина окружности примерно равна 12,56 см.

Формулы площади параллелограмма

Формула площади параллелограмма по длине стороны и высоте Площадь параллелограмма равна произведению длины его стороны и длины опущенной на эту сторону высоты. S = a · h

Формула площади параллелограмма по двум сторонам и углу между ними Площадь параллелограмма равна произведению длин его сторон умноженному на синус угла между ними. S = a · b · sin α

Формула площади параллелограмма по двум диагоналям и углу между нимиПлощадь параллелограмма равна половине произведения длин его диагоналей умноженному на синус угла между ними.

S = 1d 1d 2 sin γ 2

где S — Площадь параллелограмма, a, b — длины сторон параллелограмма, h — длина высоты параллелограмма, d ₁, d ₂ — длины диагоналей параллелограмма, α — угол между сторонами параллелограмма, γ — угол между диагоналями параллелограмма.

Вы можете воспользоваться онлайн калькулятором для расчета площади параллелограмма.

Площадь сегмента круга

Площадь кругового сегмента через угол в градусах S = R22 · π · α°180° — sinα , где S — площадь сегмента круга, R — радиус круга, α° — угол в градусах. Площадь кругового сегмента через угол в радианах S = R22 · αрад. — sinα , где S — площадь сегмента круга, R — радиус круга, α° — угол в радианах.

Формулы площади выпуклого четырехугольника

S = 1d 1 d 2 sin α 2

Формула площади описанного четырехугольника (по длине периметра и радиусу вписанной окружности) Площадь выпуклого четырехугольника равна произведению полупериметра на радиус вписанной окружности S = p · r

Формула площади четырехугольника по длине сторон и значению противоположных углов

S = √(p — a )(p — b )(p — c )(p — d ) — abcd cos2θ

где S — площадь четырехугольника,

a , b , c , d — длины сторон четырехугольника,

p = a + b + c + d 2 — полупериметр четырехугольника,

θ = α + β 2 — полусумма двух противоположных углов четырехугольника.

Формула площади четырехугольника, вокруг которого можно описать окружность S = √(p — a )(p — b )(p — c )(p — d )

Примеры решения задач

Сколько квадратных баночек с площадью основания ,1м2 поместится в коробке со стороной 30 см? Решение: S=302=900см2 или ,9м2, следовательно, 0,9:0,1 = 9 баночек.

Известно, что по диагонали квадратной танцевальной площадки по заданию проектировщика должна висеть деревянная перегородка. Длина заранее купленной перегородки составляет 6 м. Какова площадь самой площадки? Решение: S=12×62=18м2

Стороны картины — 18 и 35 сантиметров. Какова будет площадь стекла, накрывающего картину, если известно, что свободные бортики вокруг картины должны составлять по 3 сантиметра с каждой стороны? Решение: S=18+3×35+3=798см2

Какова площадь круглой площади в центре города, если известно, что мужчина со средним шагом в 50 сантиметров дойдет от ее середины до края за 10 шагов? Решение: S=π×50×102=250000π(см2)=25πм2≈78,5м2

Одно из стекол круглых очков разбилось. Мастер измерил диаметр сохранившегося стекла и пришел к выводу, что он равен 3 см. Какова должна быть площадь нового стекла, которое для очков вырежет мастер? Решение: S=14×π×32=2,25πсм2≈7,065см2

Помещение в виде эллипса решили засыпать песком. На один м2 уходит 1 мешок песка. Сколько потребуется песка на помещение с осями эллипса 20 и 36 м? Решение: S=π×a×b=180πм2≈565,2м2 значит потребуется 566 мешков.

Четырехугольники, вписанные в окружность. Теорема Птолемея

Вписанные четырехугольники и их свойства

Теорема Птолемея

Вписанные четырёхугольники и их свойства

Определение 1 . Окружностью, описанной около четырёхугольника, называют окружность, проходящую через все вершины четырёхугольника (рис.1). В этом случае четырёхугольник называют четырёхугольником, вписанным в окружность, или вписанным четырёхугольником .

Теорема 1 . Если четырёхугольник вписан в окружность, то суммы величин его противоположных углов равны 180° .

Доказательство . Угол ABC является вписанным углом, опирающимся на дугу ADC (рис.1). Поэтому величина угла ABC равна половине угловой величины дуги ADC . Угол ADC является вписанным углом, опирающимся на дугу ABC . Поэтому величина угла ADC равна половине угловой величины дуги ABC . Отсюда вытекает, что сумма величин углов ABC и ADC равна половине угловой величины дуги, совпадающей со всей окружностью, т.е. равна 180° .

Если рассмотреть углы BCD и BAD , то рассуждение будет аналогичным.

Теорема 1 доказана.

Теорема 2 (Обратная к теореме 1) . Если у четырёхугольника суммы величин его противоположных углов равны 180°, то около этого четырёхугольника можно описать окружность.

Доказательство . Докажем теорему 2 методом «от противного». С этой целью рассмотрим окружность, проходящую через вершины A , B и С четырёхугольника, и предположим, что эта окружность не проходит через вершину D . Приведём это предположение к противоречию. Рассмотрим сначала случай, когда точка D лежит внутри круга (рис.2).

Продолжим отрезок CD за точку D до пересечения с окружностью в точке E , и соединим отрезком точку E с точкой A (рис.2). Поскольку четырёхугольник ABCE вписан в окружность, то в силу теоремы 1 сумма величин углов ABC и AEC равна 180° . При этом сумма величин углов ABC и ADC так же равна 180° по условию теоремы 2. Отсюда вытекает, что угол ADC равен углу AEC . Возникает противоречие, поскольку угол ADC является внешним углом треугольника ADE и, конечно же, его величина больше, чем величина угла AEC , не смежного с ним.

Случай, когда точка D оказывается лежащей вне круга, рассматривается аналогично.

Теорема 2 доказана.

Перечисленные в следующей таблице свойства вписанных четырёхугольников непосредственно вытекают из теорем 1 и 2.

Площадь произвольного вписанного четырёхугольника можно найти по формуле Брахмагупты:

где a, b, c, d – длины сторон четырёхугольника,
а p – полупериметр, т.е.

Фигура	Рисунок	Свойство
Окружность, описанная около параллелограмма		Окружность можно описать около параллелограмма тогда и только тогда, когда параллелограмм является прямоугольником.
Окружность, описанная около ромба		Окружность можно описать около ромба тогда и только тогда, когда ромб является квадратом.
Окружность, описанная около трапеции		Окружность можно описать около трапеции тогда и только тогда, когда трапеция является равнобедренной трапецией.
Окружность, описанная около дельтоида		Окружность можно описать около дельтоида тогда и только тогда, когда дельтоид состоит из двух одинаковых прямоугольных треугольников.
Произвольный вписанный четырёхугольник

Площадь произвольного вписанного четырёхугольника можно найти по формуле Брахмагупты:

где a, b, c, d – длины сторон четырёхугольника,
а p – полупериметр, т.е.

Окружность, описанная около параллелограмма
	Окружность можно описать около параллелограмма тогда и только тогда, когда параллелограмм является прямоугольником.
Окружность, описанная около ромба
	Окружность можно описать около ромба тогда и только тогда, когда ромб является квадратом.
Окружность, описанная около трапеции
	Окружность можно описать около трапеции тогда и только тогда, когда трапеция является равнобедренной трапецией.
Окружность, описанная около дельтоида
	Окружность можно описать около дельтоида тогда и только тогда, когда дельтоид состоит из двух одинаковых прямоугольных треугольников.
Произвольный вписанный четырёхугольник

Окружность, описанная около параллелограмма

Окружность можно описать около параллелограмма тогда и только тогда, когда параллелограмм является прямоугольником.

Окружность, описанная около ромба

Окружность можно описать около ромба тогда и только тогда, когда ромб является квадратом.

Окружность, описанная около трапеции

Окружность можно описать около трапеции тогда и только тогда, когда трапеция является равнобедренной трапецией.

Окружность, описанная около дельтоида

Окружность можно описать около дельтоида тогда и только тогда, когда дельтоид состоит из двух одинаковых прямоугольных треугольников.

Произвольный вписанный четырёхугольник

Площадь произвольного вписанного четырёхугольника можно найти по формуле Брахмагупты:

где a, b, c, d – длины сторон четырёхугольника,
а p – полупериметр, т.е.

Теорема Птолемея

Теорема Птолемея . Произведение диагоналей вписанного четырёхугольника равно сумме произведений противоположных сторон.

Доказательство . Рассмотрим произвольный четырёхугольник ABCD , вписанный в окружность (рис.3).

Докажем, что справедливо равенство:

Для этого выберем на диагонали AC точку E так, чтобы угол ABD был равен углу CBE (рис. 4).

Заметим, что треугольник ABD подобен треугольнику BCE . Действительно, у этих треугольников по два равных угла: угол ABD равен углу CBE (по построению точки E ), угол ADB равен углу ACB (эти углы являются вписанными углами, опирающимися на одну и ту же дугу). Следовательно, справедлива пропорция:

откуда вытекает равенство:

(1)

Заметим, что треугольник ABE подобен треугольнику BCD . Действительно, у этих треугольников по два равных угла: угол ABE равен углу DBC (углы ABD и EBC равны по построению, угол DBE – общий), угол BAC равен углу BDC (эти углы являются вписанными углами, пирающимися на одну и ту же дугу). Следовательно, справедлива пропорция:

📽️ Видео