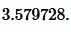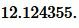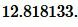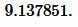Боковая сторона равнобедренного треугольника равна 22, угол при вершине, противолежащей основанию, равен Найдите диаметр описанной окружности этого треугольника.
Это задание ещё не решено, приводим решение прототипа.
Боковая сторона равнобедренного треугольника равна 1, угол при вершине, противолежащей основанию, равен 120°. Найдите диаметр описанной окружности этого треугольника.
Сумма двух равных углов при основании треугольника равна 60°, поэтому каждый из них равен 30°. Тогда по теореме синусов
- Найдите диаметр окружности, описанной около равнобедренного треугольника с углом 120° и боковой стороной 12 см?
- Угол при вершине равнобедренного треугольника = 120, а боковая сторона 4 см?
- Угол при вершине равнобедренного треугольника = 120, а боковая сторона 2 см?
- Найдите длину окружности описанной около равнобедренного треугольника с основанием а и боковой стороной б?
- Боковая сторона равнобедренного треугольника равна 5?
- Найдите диаметр окружности, описанной около равнобедренного треугольника с углом 60 градусов и боковой стороной 12 см?
- ПРОШУ, ПОМОГИТЕ?
- Угол при основании равнобедренного треугольника равен 30°, боковая сторона 16см?
- Боковая сторона равнобедренного треугольника равна 4?
- Найдите длину боковой стороны равнобедренного прямоугольного треугольника, если известно, что диаметр описанной около него окружности равен 56см?
- Угол при вершине равнобедренного треугольника равен 120 градусов а Боковая сторона на 2 сантиметра Найдите диаметр окружности описанной около него?
- Радиус описанной окружности около равнобедренного треугольника онлайн
- 1. Радиус окружности описанной около равнобедренного треугольника, если известны основание a и боковая сторона b=c
- 2. Радиус окружности описанной около равнобедренного треугольника, если известны основание a и противолежащий угол A
- 3. Радиус окружности описанной около равнобедренного треугольника, если известны боковая сторона b=c треугольника и угол между боковыми сторонами A
- 4. Радиус окружности описанной около равнобедренного треугольника, если известны основание a и прилежащий угол B=C
- 💡 Видео
Видео:Геометрия Найдите диаметр окружности, описанной около прямоугольного треугольника, если один из егоСкачать

Найдите диаметр окружности, описанной около равнобедренного треугольника с углом 120° и боковой стороной 12 см?
Геометрия | 5 — 9 классы
Найдите диаметр окружности, описанной около равнобедренного треугольника с углом 120° и боковой стороной 12 см.
ΔABC — равнобедренный, угол B = 120°.
Тогда углы при основании будут по 30°
O — центр окружности.
Угол АОС = 360° — уголABC * 2 = 360° — 120° * 2 = 120°.
ΔAOC — равнобедренный, т.
К. ОА = ОC (радиусы).
Углы при основании будут тоже по 30°.
К. все углы у них попарно равны и сторона АС — общая⇒ АВ = ОА = 12см.
ОА — радиус, диаметр окружности = 2 * ОА = 24 см.
Чертеж сами сделаете?
Видео:Задача 6 №27900 ЕГЭ по математике. Урок 128Скачать

Угол при вершине равнобедренного треугольника = 120, а боковая сторона 4 см?
Угол при вершине равнобедренного треугольника = 120, а боковая сторона 4 см.
Найдите диаметр окружности описанной около него.
Видео:Как найти диаметр окружности, описанной около равнобедренного треугольникаСкачать

Угол при вершине равнобедренного треугольника = 120, а боковая сторона 2 см?
Угол при вершине равнобедренного треугольника = 120, а боковая сторона 2 см.
Найдите диаметр окружности описанной около него.
ТОЛЬКО пожалуста без синусов решать.
Видео:№694. Найдите диаметр окружности, вписанной в прямоугольный треугольник, если гипотенузаСкачать
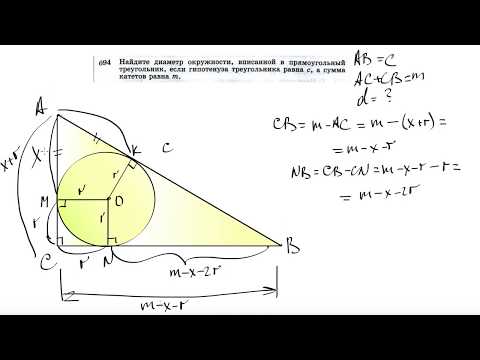
Найдите длину окружности описанной около равнобедренного треугольника с основанием а и боковой стороной б?
Найдите длину окружности описанной около равнобедренного треугольника с основанием а и боковой стороной б.
Видео:Радиус и диаметрСкачать

Боковая сторона равнобедренного треугольника равна 5?
Боковая сторона равнобедренного треугольника равна 5.
Угол при вершине, противолежащий основанию равен 120градусам.
Найдите диаметр окружности, описанной около этого треугольника.
Видео:Свойство окружности, описанной около равнобедренного треугольникаСкачать

Найдите диаметр окружности, описанной около равнобедренного треугольника с углом 60 градусов и боковой стороной 12 см?
Найдите диаметр окружности, описанной около равнобедренного треугольника с углом 60 градусов и боковой стороной 12 см.
Видео:Нахождение диаметра описанной окружностиСкачать
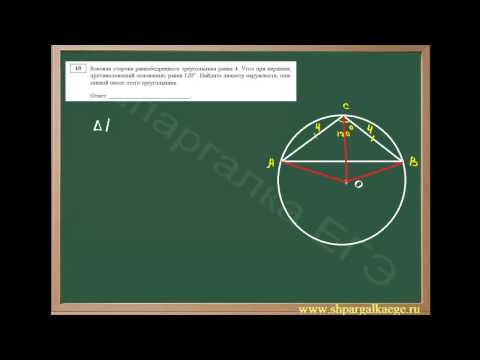
ПРОШУ, ПОМОГИТЕ?
Найдите диаметр окружности, описанной около равнобедренного треугольника с углом 120° и боковой стороной 12 см.
Видео:ЕГЭ 6 номер. Нахождение диаметра описанной окружности около равнобедренного треугольникаСкачать

Угол при основании равнобедренного треугольника равен 30°, боковая сторона 16см?
Угол при основании равнобедренного треугольника равен 30°, боковая сторона 16см.
Найдите диаметр окружности, описанной около этого треугольника.
Видео:№702. В окружность вписан треугольник ABC так, что АВ — диаметр окружности. Найдите углыСкачать

Боковая сторона равнобедренного треугольника равна 4?
Боковая сторона равнобедренного треугольника равна 4.
Угол при вершине противолежащий основанию равен 120° Найдите диаметр окружности описанной около этого треугольника.
Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Найдите длину боковой стороны равнобедренного прямоугольного треугольника, если известно, что диаметр описанной около него окружности равен 56см?
Найдите длину боковой стороны равнобедренного прямоугольного треугольника, если известно, что диаметр описанной около него окружности равен 56см.
Видео:№707. Угол, противолежащий основанию равнобедренного треугольника, равен 120°, боковая сторонаСкачать

Угол при вершине равнобедренного треугольника равен 120 градусов а Боковая сторона на 2 сантиметра Найдите диаметр окружности описанной около него?
Угол при вершине равнобедренного треугольника равен 120 градусов а Боковая сторона на 2 сантиметра Найдите диаметр окружности описанной около него.
Перед вами страница с вопросом Найдите диаметр окружности, описанной около равнобедренного треугольника с углом 120° и боковой стороной 12 см?, который относится к категории Геометрия. Уровень сложности соответствует учебной программе для учащихся 5 — 9 классов. Здесь вы найдете не только правильный ответ, но и сможете ознакомиться с вариантами пользователей, а также обсудить тему и выбрать подходящую версию. Если среди найденных ответов не окажется варианта, полностью раскрывающего тему, воспользуйтесь «умным поиском», который откроет все похожие ответы, или создайте собственный вопрос, нажав кнопку в верхней части страницы.
Пусть О — точка пересечения диагоналей прямоугольника. Расстоянием от точки О до стороны АВ будет перпендикуляр ОН, опущенный из точки О к АВ. ОН⊥АВ, ВС⊥АВ, значит ОН║ВС. Диагонали прямоугольника равны и точкой пересечения делятся пополам. Значит..
Пусть 1 угол х тогда 2 угол х + 24 × + × + 24 = 180 2× = 156 × = 78 — 1 угол 2 — 78 + 24 = 102.
Для удобства решения , перенесём симметрично точку K в нижнее основание ABCD (все пересечения абсолютно те же) то есть точкам A, B, C, D соответствуют точки A1, B1, C1, D1. Тогда точка K пересечения прямых BM и AN . Найдём соотношение BK / KM , про..
3 — 1, а 5 — 2. Точно не знаю.
3) 1, решение : 180 — 65 = 115 115 = 75 + 40 5) 1, решение : ОКВ = 90 градусов, значит OKV = 45 градусов, углы VOK = VKO, значит треугольник vko равнобедренный, то есть VO = VK, отсюда BO = OV умножить на 2, что равно 7 * 2 = 14 вроде так, , , , , , ..
Так оно же разное может быть.
Любая сторона треугольника меньше суммы двух других сторон и больше их разности. 7 + 13 = 20 — длина третьей стороны не может превышать 19 см. 13 — 7 = 6 — длина третьей стороны не может быть меньше 7 см. Все простые числа от 7 до 19 : 7, 11, 13, ..
|КР| = ✓((3 — ( — 3))² + ( — 4 — 2)²) = ✓(36 + 36) = ✓72 = 6✓2 Пусть М — середина отрезка. Её координаты равны полусумме соответствующих координат точек К и Р М(( — 3 + 3) / 2 ; (2 + ( — 4)) / 2) М(0 ; — 1).
Смежные углы = 180 ° = >.
Биссектрисы углов отсекают от прямоугольника равнобедркнные треугольники (свойство биссектрис). В случае, когда биссектрисы пересекаются на стороне ВС, имеем : АВ = ВМ и CD = МС. Значит сторона ВС = АВ + CD или 2 * АВ. Полупериметр равен 42 : 2 = ..
Видео:найти радиус окружности, описанной вокруг треугольникаСкачать

Радиус описанной окружности около равнобедренного треугольника онлайн
С помощю этого онлайн калькулятора можно найти радиус описанной окружности около любого треугольника. Для нахождения радиуса окружности описанной около треугольника введите известные данные в ячейки и нажмите на кнопку «Вычислить». Теоретическую часть и численные примеры смотрите ниже.
| Открыть онлайн калькулятор |
Видео:ОГЭ Задание 16 Описанная окружность ДиаметрСкачать

1. Радиус окружности описанной около равнобедренного треугольника, если известны основание a и боковая сторона b=c
Пусть известны основание a равнобедренного треугольника и боковая сторона b=c. Найдем радиус описанной окружности около равнобедренного треугольника. На странице Радиус окружности описанной около треугольника онлайн была выведена формула вычисления радиуса R описанной около любого треугольника окружности:
| ( small R=frac<large 4 cdot sqrt >. ) | (1) |
где p вычисляется из формулы:
| ( small p= frac. ) | (2) |
Учитывая, что у нас треугольник равнобедренный, т.е. b=c, имеем:
| ( small p= frac=b+ frac, ) | (3) |
| ( small p-a= b- frac, ) | (4) |
| ( small p-b= frac, ) | (5) |
Подставляя (3)−(5) в (1) и учитывая, что b=c, получим:
| ( small R=frac<large 4 cdot frac cdot sqrt<left ( b+fracright)left ( b-fracright)>> ) ( small =frac<large 2 cdot sqrt< b^2-frac>> ) ( small =frac< sqrt> ,) |
| ( small R=frac< sqrt>. ) | (6) |
Пример 1. Известны основание ( small a=7 ) и боковая сторона ( small b=frac ) равнобедренного треугольника. Найти радиус окружности описанной около треугольника.
Решение. Для нахождения радиуса окружности описанной около треугольника воспользуемся формулой (6).
Подставим значения ( small a=7 ) и ( small b=frac ) в (6):
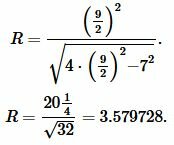 |
Ответ:
Видео:Геометрия. Задание 17. Подготовка к ОГЭ и ЕГЭ по математике. Дистанционное обучениеСкачать

2. Радиус окружности описанной около равнобедренного треугольника, если известны основание a и противолежащий угол A
Пусть известны сторона a и противолежащий угол A. Формула для нахождения радиуса окружности описанной около равнобедренного треугольника по основанию и противолежащему углу аналогична формуле для нахождения радиуса окружности описанной около произвольного треугольника:
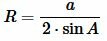 . . | (7) |
Пример 2. Сторона основание равнобедренного треугольника равна:( small a=21 ) а противолежащий угол ( small angle A=60°.) Найти радиус окружности описанной около треугольника.
Решение. Для нахождения радиуса окружности описанной около треугольника воспользуемся формулой (7). Подставим значения ( small a=21 ) и ( small angle A=60° ) в (7):
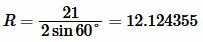 . . |
Ответ:
Видео:2031 окружность центром в точке О описана около равнобедренного треугольника ABCСкачать

3. Радиус окружности описанной около равнобедренного треугольника, если известны боковая сторона b=c треугольника и угол между боковыми сторонами A
Пусть известны боковая сторона b=c равнобедренного треугольника и угол между боковыми сторонами A. Найдем радиус описанной окружности около равнобедренного треугольника.
На странице Радиус описанной окружности около треугольника онлайн была выведена формула для нахождения радиуса описанной окружности около треугольника при известных сторонах и углу между ними:
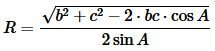 . . | (8) |
Подставляя в (8) c=b, получим:
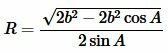 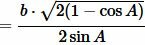 |
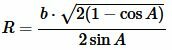 . . | (9) |
Пример 3. Известны основание ( small a=21 ) равнобедренного треугольника и угол между боковыми сторонами: ( small angle A=70°. ) Найти радиус окружности описанной около треугольника.
Решение. Для нахождения радиуса окружности описанной около треугольника воспользуемся формулой (9). Подставим значения ( small a=21; ) и ( small angle A=70° ) в (9):
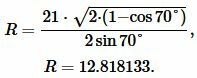 |
Ответ:
Видео:Геометрия. ОГЭ по математике. Задание 16Скачать

4. Радиус окружности описанной около равнобедренного треугольника, если известны основание a и прилежащий угол B=C
Пусть известны основание a равнобедренного треугольника и прилежащие к ней угол B=C. Найдем радиус описанной окружности около треугольника. На странице Радиус описанной окружности около треугольника онлайн была выведена формула для нахождения радиуса описанной окружности около треугольника при известной стороне и прилежащим двум углам:
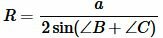 . . | (10) |
Подставляя ( small C=B ) в (10), получим требуемую формулу:
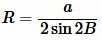 . . | (11) |
Пример 4. Известны основание равнобедренного треугольника ( small a=14 ) и прилежащий к ней угол: ( small angle B=25°. ) Найти радиус окружности описанной около треугольника.
Решение. Для нахождения радиуса окружности описанной около треугольника воспользуемся формулой (11). Подставим значения ( small a=14 ) и ( small angle B=25° ) в (11):
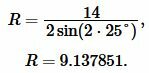 |
Ответ:
💡 Видео
№706. Найдите сторону равностороннего треугольника, если радиус описанной около него окружностиСкачать

Периметр правильного шестиугольника равен 72. Найдите диаметр описанной окружности.Скачать

Радиус описанной окружностиСкачать

Геометрия 9 класс. Радиус описанной и вписанной окружности треугольника. Формулы радиуса.Скачать