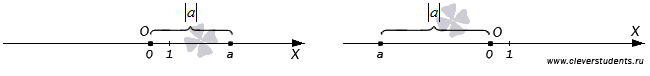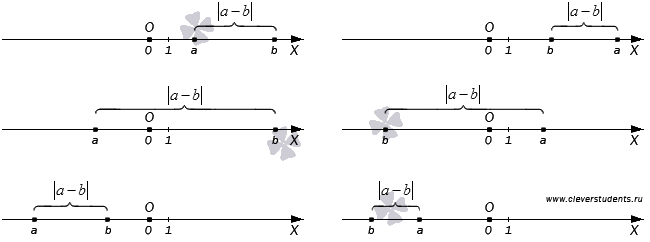Неравенства треугольника для модулей

В этой статье введем и очень подробно разберем такое важное понятие, как модуль числа. Разберемся, откуда модуль взялся, какими свойствами обладает. Научимся решать уравнения и неравенства с модулем.

Видео:✓ Неравенство треугольника | Ботай со мной #126 | Борис ТрушинСкачать

«Величина» числа

Сначала попытаемся сформулировать понятие о «величине» числа. Из этого понятия естественным образом получим понимание, откуда взялся и как определить модуль.

Геометрический смысл

Представьте, что вы стоите в точке 0 на числовой оси. Слева от вас, в точке − 1 0 0 , находится школа. Справа, в точке 5 0 , находится ваш дом. Математически число − 1 0 0 меньше, чем 5 0 . Но вот идти до школы 1 0 0 метров влево гораздо дольше, чем пройти 5 0 метров до дома вправо. В этом смысле «величина» пройденного расстояния в − 1 0 0 метров больше, чем 5 0 метров.

Пусть теперь школа находится в точке − 1 0 , а дом в точке 1 0 . Математически вновь получаем, что − 1 0 меньше 1 0 . Но вот нам, находящимся в 0 , совершенно нет разницы: идти − 1 0 метров влево или 1 0 метров вправо. В обоих случаях мы пройдем 1 0 метров. То есть, по «величине» числа − 1 0 и 1 0 равны.

Количественный смысл

Рассмотрим числа 5 0 и − 1 0 0 . В математическом смысле − 1 0 0 гораздо меньше 5 0 . А давайте посмотрим на эти числа под другим углом. У вас есть всего 5 0 рублей и вы задолжали другу. Ваш долг составляет − 1 0 0 рублей. В этом смысле «величина» вашего долга в − 1 0 0 рублей гораздо больше имеющихся у вас 5 0 рублей. Получается, что математически − 1 0 0 меньше 5 0 , но по «величине» − 1 0 0 больше 5 0 .

Теперь рассмотрим числа − 1 0 и 1 0 . Математически, опять же, − 1 0 меньше 1 0 . Но, пользуясь нашей аналогией с долгом, своими 1 0 рублями вы полностью покроете долг в − 1 0 рублей. То есть, по «величине» число − 1 0 равно числу 1 0 .

Понятие величины

Мы поняли, что каждое число имеет свою «величину». Причем эта величина не зависит от того, положительным или отрицательным является число. Можно даже сказать, что «величина» числа это и есть само число, от которого «отбросили» его знак.

Видео:Доказательство свойств модуля, №25.Скачать

Модуль числа

Сформулируем на строгом языке математики наше интуитивное представление о «величине» числа, которое мы сформировали в предыдущем разделе.

Модуль или абсолютная величина вещественного числа x — само число x , если оно неотрицательно, иначе − x .

Допустим, мы хотим найти модуль какого-то числа a . Согласно определению, нам надо провести элементарную проверку. Если число a положительное или равно 0 , то модулем a и является само a . Если же a меньше 0 , то результатом модуля будет − a .

∣ 5 ∣ = 5 ∣ 0 ∣ = 0 ∣ − 1 2 ∣ = − ( − 1 2 ) = 1 2

Легко убедиться, что модуль числа полностью соответсвует по смыслу «величине» числа, рассмотренной в предыдущем разделе. Там мы утверждали, что по «величине» − 1 0 0 больше 5 0 , а − 1 0 равно 1 0 . И действительно:

∣ − 1 0 0 ∣ = 1 0 0 ∣ − 1 0 ∣ = 1 0 ​ ∣ 5 0 ∣ = 5 0 ∣ − 1 0 0 ∣ > ∣ 5 0 ∣ ∣ 1 0 ∣ = 1 0 ∣ − 1 0 ∣ = ∣ 1 0 ∣ ​

Положение знака нестрогого неравенства в определении модуля не имеет значения:

Обозначим второе определение модуля числа x как ∣ x ∣ ′ . Покажем, что какой x не возьми, будет выполняться ∣ x ∣ = ∣ x ∣ ′ .

Пусть x > 0 . По классическому определению ∣ x ∣ = x . По второму: ∣ x ∣ ′ = x . То есть ∣ x ∣ = ∣ x ∣ ′ .

Пусть x = 0 . По классическому определению ∣ 0 ∣ = 0 . А вот во втором определении 0 попадает уже под второе условие, то есть ∣ 0 ∣ ′ = − 0 = 0 . Опять имеем ∣ 0 ∣ = ∣ 0 ∣ ′ .

Наконец, пусть x 0 . По классическому определению ∣ x ∣ = − x . У второго определения та же ситуация: ∣ x ∣ ′ = − x . Получается, что и в этом случае ∣ x ∣ = ∣ x ∣ ′ .

Итак, мы рассмотрели все возможные значения для x и во всех случаях ∣ x ∣ = ∣ x ∣ ′ . Это и означает, что между двумя определениями нет никакой разницы ■

Такое определение иногда бывает полезно. Например, если x лежит в следующих пределах: − 1 0 ≤ x ≤ 0 , то можно сразу сказать, что ∣ x ∣ = − x , даже несмотря на то, что для x = 0 так выражаться будет некорректно, ведь ∣ 0 ∣ = 0 , а не − 0 .

Видео:Неравенства треугольника. 7 класс.Скачать

Свойства модуля

У модуля есть очень много полезных свойств, которые сильно помогают при решении уравнений, неравенств, доказательстве теорем и так далее. Рассмотрим самые полезные из них. Все свойства ниже формулируем для любых вещественных чисел x и y .

Очевидные свойства

Наиболее очевидные свойства модуля напрямую вытекают из рассмотренного ранее понятия о «величине» числа. Например, мы определили «величину» числа как само число с «отброшенным» знаком. Это означает, что «величина» не может быть отрицательной.

Видео:МОДУЛЬ 😉 #егэ #математика #профильныйегэ #shorts #огэСкачать

Модули

В этой лекции мы рассмотрим:

• Модули
• неравенства с участием модулей
• Теорема 1.2.2 (√ a 2 =|a|)
• Теорема неравенства

1.2.1 Определение

Пример
|5| = 5 Так как 5 > 0
|-4| = -(-4) = 4 Так как -4

Замечание
|a| есть не отрицательным числом для всех значений a и
-|a|≤ a ≤ |a|

Если a является негативным тогда -a позитивно и +a отрицательное.

Пример
Решите уравнение |x-3|=4
Решение

Уравнение имеет 2 решения: -1 и 7.

Пример
Решите уравнение |3x-2|=|5x+4|

Уравнение имеет 2 решения: -3 и $-frac$.

Позитивный корень квадрата числа равен этому числу.

ТЕОРЕМА 1.2.2
Для любого действительного числа a
√ a 2 = |a|
e.g.
√ (-4) 2 = √ 16 = 4 = |-4|

ТЕОРЕМА 1.2.3
Если a и b действительные числа, тогда

1. |-a| = |a| число a и его отрицательное значение имеет одинаковые модули.
2. |ab| = |a||b| Модуль произведения двух чисел есть произведение их модулей.
3. |a/b| = |a|/|b| Модуль отношения двух чисел есть отношение их модулей.

Доказательство
Из теоремы 1.2.2

(a) |-a| = √ (-a) 2 = √ a 2 = |a|

(b) |ab| = √ (ab) 2 = √ a 2 b 2 = √ a 2 √ b 2 = |a||b|

(b) |2.-3| = |-6| = 6 = |2|.|3| = 6

Результат (b) вышеизложенной теоремы может быть применено к трем или более членам.
Для n действительных чисел
a₁, a₂, a₃. a_n
(a) |a₁ a₂ . a_n| = |a₁| |a₂| . |a_n|
(b) |a n | = |a| n

Геометрическое представление модуля

Где A и B есть точки с координатами a и b. Расстояние между A и B есть
$text=beginb-a text a b \ 0 text a = b end$

Теорема 1.2.4 (Формула расстояния)
Если A и B — точки на координатной прямой с координатами a и b соответственно, тогда расстояние d между A и B
d = |b — a|

ТАБЛИЦА 1.2.2 (a)
|x-a| 0)

Альтернативная форма -k

Пример
Неравенство
|x-3| Пример
Решите |x+4| ≥ 2

Объединение двух неравенств дает
(-∞ , -6] ∪ [-2 , +∞ )

На численной прямой

Не всегда верно, что
|a+b| = |a| + |b|
например
если a = 2 и b = -3, тогда a+b = -1 и поэтому |a+b| = |-1| = 1
в то время как
|a|+|b| = |2|+|-3| = 2+3 = 5 поэтому |a+b| = |a|+|b|

1.2.5 ТЕОРЕМА — (Неравенство треугольника)
Если a b тогда |a+b| ≤ |a|+|b|
Доказательство
Так как для любого действительного числа a и b, мы знаем, что
-|a| ≤ a ≤ |a| and -|b| ≤ b ≤ |b|
-|a| ≤ a ≤ |a|
+
-|b| ≤ b ≤ |b|
______________
= -|a| + -|b| ≤ a+b ≤ |a|+|b|
______________________________________________
Сейчай мы имеем два случая:

Первый случай, где a+b ≥ 0
определенно: a+b=|a+b|
Отсюда
|a+b| ≤ |a|+|b|

Второй случай где a+b _______________________________ →

Видео:Свойства модуля: линейность, неравенство треугольника, модуль разности модулейСкачать

Разность модулей и модуль разности

Существуют следующие свойства модуля действительных чисел:

Проведем доказательства, рассматривая различные случаи значений a и b .

Доказательство 1) |a + b| ≤ |a| + |b|:

Если a и b – положительные числа, то их модули совпадают с их значениями: |a| = a, |b| = b . Из этого следует, что |a + b| = |a| + |b| .

Если a – отрицательное число, а b – положительное число, то выражение |a + b| можно записать как |b – a| . Выражение же |a| + |b| равно сумме абсолютных значений a и b , что больше, чем b – a . Поэтому |a + b| .

Если b – отрицательное число, а a – положительное, то |a + b| принимает вид |a – b| , что также меньше суммы модулей |a| + |b| .

Если a и b – отрицательные числа, то получим |–a – b| . Результат этого выражения равен |a + b| (т. к. |–a – b| = |–(a + b)| = |a + b| ). Но уже было доказано, что |a + b| = |a| + |b| , следовательно и |–a – b| = |a| + |b| .

Доказательство 2) |ab| = |a| × |b|:
Здесь, в отличие от сложения, рассматривать все случаи особо не требуется, т. к. абсолютное значение произведения любых чисел (положительных ли, отрицательных ли) не зависит от знаков множителей. В выражении |ab| мы сначала перемножаем числа, а потом «отбрасываем» знак (отрицательный, если он есть), в выражении |a| × |b| сначала избавляемся от знаков, а потом перемножаем. Но от того, в какой момент был взят модуль (до или после умножения), не зависит абсолютное значение произведения.

Доказательство 3) , a ≠ 0:

Если a – положительное число, то |a| = a и, следовательно, доказываемое равенство верно, т. к. и правая и левая части равны 1/ a .

Доказательство 4) |a – b| ≥ |a| – |b|:

Если a и b – положительные числа, то их модули совпадают с самими числами. Поэтому |a – b| = |a| – |b| , потому что можно не брать модули вообще и тогда с двух сторон получим a – b .

Если a – положительное число, а b – отрицательное, то выражение |a – b| примет вид |a + b| , что больше, чем |a| – |b| .

Если a – отрицательное число, а b – положительное, то имеем |–a – b| = |–(a + b)| = |a + b| , что больше, чем |a| – |b| .

В этой статье мы детально разберем модуль числа. Мы дадим различные определения модуля числа, введем обозначения и приведем графические иллюстрации. При этом рассмотрим различные примеры нахождения модуля числа по определению. После этого мы перечислим и обоснуем основные свойства модуля. В конце статьи поговорим о том, как определяется и находится модуль комплексного числа.

Навигация по странице.

Видео:Неравенства треугольника. Практическая часть. 7 класс.Скачать

Модуль числа – определение, обозначение и примеры

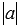
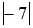
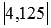
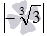
Сначала введем обозначение модуля числа. Модуль числа a будем записывать как , то есть, слева и справа от числа будем ставить вертикальные черточки, образующие знак модуля. Приведем пару примеров. Например, модуль целого числа −7 можно записать как ; модуль рационального числа 4,125 записывается как , а модуль иррационального числа имеет запись вида .

Так мы определились с обозначением, теперь пришло время дать определение модуля числа. Чтобы хорошо понять определение модуля числа необходимо хорошо владеть материалом статьи положительные и отрицательные числа, а также статьи противоположные числа.

Следующее определение модуля относится к действительным числам, а следовательно, и к натуральным числам, и к целым, и к рациональным, и к иррациональным числам, как к составляющим частям множества действительных чисел. О модуле комплексного числа мы поговорим в последнем пункте этой статьи.

Модуль числа a – это либо само число a , если a – положительное число, либо число −a , противоположное числу a , если a – отрицательное число, либо 0 , если a=0 .

Озвученное определение модуля числа часто записывают в следующем виде , эта запись означает, что , если a>0 , , если a=0 , и , если a .

Запись можно представить в более компактной форме . Эта запись означает, что , если ( a больше или равно 0 ), и , если a .

Также имеет место и запись . Здесь отдельно следует пояснить случай, когда a=0 . В этом случае имеем , но −0=0 , так как нуль считают числом, которое противоположно самому себе.

Приведем примеры нахождения модуля числа с помощью озвученного определения. Для примера найдем модули чисел 15 и . Начнем с нахождения . Так как число 15 – положительное, то его модуль по определению равен самому этому числу, то есть, . А чему равен модуль числа ? Так как — отрицательное число, то его модуль равен числу, противоположному числу , то есть, числу . Таким образом, .

В заключение этого пункта приведем один вывод, который очень удобно применять на практике при нахождении модуля числа. Из определения модуля числа следует, что модуль числа равен числу под знаком модуля без учета его знака, а из рассмотренных выше примеров это очень отчетливо видно. Озвученное утверждение объясняет, почему модуль числа называют еще абсолютной величиной числа. Так модуль числа и абсолютная величина числа – это одно и то же.

Видео:Неравенства с модулем | Математика | TutorOnlineСкачать

Модуль числа как расстояние

Геометрически модуль числа можно интерпретировать как расстояние. Приведем определение модуля числа через расстояние.

Модуль числа a – это расстояние от начала отсчета на координатной прямой до точки, соответствующей числу a.

Данное определение согласуется с определением модуля числа, данного в первом пункте. Поясним этот момент. Расстояние от начала отсчета до точки, которой соответствует положительное число, равно этому числу. Нулю соответствует начало отсчета, поэтому расстояние от начала отсчета до точки с координатой 0 равно нулю (не нужно откладывать ни одного единичного отрезка и ни одного отрезка, составляющего какую-нибудь долю единичного отрезка, чтобы от точки O попасть в точку с координатой 0 ). Расстояние от начала отсчета до точки с отрицательной координатой равно числу, противоположному координате данной точки, так как равно расстоянию от начала координат до точки, координатой которой является противоположное число.

Например, модуль числа 9 равен 9 , так как расстояние от начала отсчета до точки с координатой 9 равно девяти. Приведем еще пример. Точка с координатой −3,25 находится от точки O на расстоянии 3,25 , поэтому .

Озвученное определение модуля числа является частным случаем определения модуля разности двух чисел.

Модуль разности двух чисел a и b равен расстоянию между точками координатной прямой с координатами a и b .

То есть, если даны точки на координатной прямой A(a) и B(b) , то расстояние от точки A до точки B равно модулю разности чисел a и b . Если в качестве точки В взять точку O (начало отсчета), то мы получим определение модуля числа, приведенное в начале этого пункта.

Видео:7 класс, 34 урок, Неравенство треугольникаСкачать

Определение модуля числа через арифметический квадратный корень

Иногда встречается определение модуля через арифметический квадратный корень.

Модуль числа a – это арифметический квадратный корень из квадрата числа a , то есть, .

Для примера вычислим модули чисел −30 и на основании данного определения. Имеем . Аналогично вычисляем модуль двух третьих: .

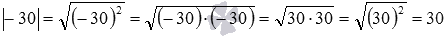
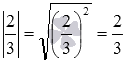
Определение модуля числа через арифметический квадратный корень также согласуется с определением, данным в первом пункте этой статьи. Покажем это. Пусть a – положительное число, при этом число −a – отрицательное. Тогда и , если же a=0 , то .

Видео:Неравенство треугольникаСкачать

Свойства модуля

Модулю присущ ряд характерных результатов — свойства модуля. Сейчас мы приведем основные и наиболее часто используемые из них. При обосновании этих свойств мы будем опираться на определение модуля числа через расстояние.

Начнем с самого очевидного свойства модуля – модуль числа не может быть отрицательным числом. В буквенном виде это свойство имеет запись вида для любого числа a . Это свойство очень легко обосновать: модуль числа есть расстояние, а расстояние не может выражаться отрицательным числом.

Переходим к следующему свойству модуля. Модуль числа равен нулю тогда и только тогда, когда это число есть нуль. Модуль нуля есть нуль по определению. Нулю соответствует начало отсчета, никакая другая точка на координатной прямой нулю не соответствует, так как каждому действительному числу поставлена в соответствие единственная точка на координатной прямой. По этой же причине любому числу, отличному от нуля, соответствует точка, отличная от начала отсчета. А расстояние от начала отсчета до любой точки, отличной от точки O , не равно нулю, так как расстояние между двумя точками равно нулю тогда и только тогда, когда эти точки совпадают. Приведенные рассуждения доказывают, что нулю равен лишь модуль нуля.

Идем дальше. Противоположные числа имеют равные модули, то есть, для любого числа a . Действительно, две точки на координатной прямой, координатами которых являются противоположные числа, находятся на одинаковом расстоянии от начала отсчета, значит модули противоположных чисел равны.

Следующее свойство модуля таково: модуль произведения двух чисел равен произведению модулей этих чисел, то есть, . По определению модуль произведения чисел a и b равен либо a·b , если , либо −(a·b) , если . Из правил умножения действительных чисел следует, что произведение модулей чисел a и b равно либо a·b , , либо −(a·b) , если , что доказывает рассматриваемое свойство.

Модуль частного от деления a на b равен частному от деления модуля числа a на модуль числа b , то есть, . Обоснуем это свойство модуля. Так как частное равно произведению , то . В силу предыдущего свойства имеем . Осталось лишь воспользоваться равенством , которое справедливо в силу определения модуля числа.

Следующее свойство модуля записывается в виде неравенства: , a , b и c – произвольные действительные числа. Записанное неравенство представляет собой ни что иное как неравенство треугольника. Чтобы это стало понятно, возьмем точки A(a) , B(b) , C(c) на координатной прямой, и рассмотрим вырожденный треугольник АВС , у которого вершины лежат на одной прямой. По определению модуля разности равен длине отрезка АВ , — длине отрезка АС , а — длине отрезка СВ . Так как длина любой стороны треугольника не превосходит сумму длин двух других сторон, то справедливо неравенство , следовательно, справедливо и неравенство .

Только что доказанное неравенство намного чаще встречается в виде . Записанное неравенство обычно рассматривают как отдельное свойство модуля с формулировкой: «Модуль суммы двух чисел не превосходит сумму модулей этих чисел». Но неравенство напрямую следует из неравенства , если в нем вместо b положить −b , и принять c=0 .

Видео:Как решать неравенства с модулем. Два модуля в неравенстве.Скачать

Модуль комплексного числа

Дадим определение модуля комплексного числа. Пусть нам дано комплексное число, записанное в алгебраической форме 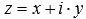, где x и y – некоторые действительные числа, представляющие собой соответственно действительную и мнимую части данного комплексного числа z , а – мнимая единица.

Модулем комплексного числа z=x+i·y называется арифметический квадратный корень из суммы квадратов действительной и мнимой части данного комплексного числа.

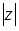
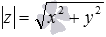
Модуль комплексного числа z обозначается как , тогда озвученное определение модуля комплексного числа может быть записано в виде .

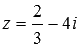
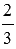
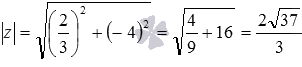
Данное определения позволяет вычислить модуль любого комплексного числа в алгебраической форме записи. Для примера вычислим модуль комплексного числа . В этом примере действительная часть комплексного числа равна , а мнимая – минус четырем. Тогда по определению модуля комплексного числа имеем .

Геометрическую интерпретацию модуля комплексного числа можно дать через расстояние, по аналогии с геометрической интерпретацией модуля действительного числа.

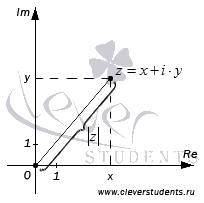
Модуль комплексного числа z – это расстояние от начала комплексной плоскости до точки, соответствующей числу z в этой плоскости.

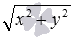
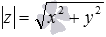
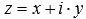
По теореме Пифагора расстояние от точки O до точки с координатами (x, y) находится как , поэтому, , где . Следовательно, последнее определение модуля комплексного числа согласуется с первым.

Данное определение также позволяет сразу указать, чему равен модуль комплексного числа z , если оно записано в тригонометрической форме как или в показательной форме . Здесь . Например, модуль комплексного числа равен 5 , а модуль комплексного числа равен .

Можно также заметить, что произведение комплексного числа на комплексно сопряженное число дает сумму квадратов действительной и мнимой части. Действительно, . Полученное равенство позволяет дать еще одно определение модуля комплексного числа.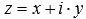

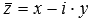
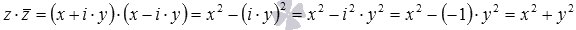
Модуль комплексного числа z – это арифметический квадратный корень из произведения этого числа и числа, комплексно сопряженного с ним, то есть, .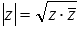

В заключение отметим, что все свойства модуля, сформулированные в соответствующем пункте, справедливы и для комплексных чисел.

Хочешь подготовиться к ОГЭ или ЕГЭ по математике на отлично?

Хочешь проверить свои силы и узнать результат насколько ты готов к ЕГЭ или ОГЭ?

Важное замечание!
Если вместо формул ты видишь абракадабру, почисти кэш. Как это сделать в твоем браузере написано здесь: «Как почистить кэш браузера».

Модуль числа — это такая забавная концепция в математике, с пониманием которой у многих людей возникают трудности.

А между тем она проста как апельсин. Но чтобы ее понять, давай сначала разберемся зачем нужен модуль.

Вот смотри, ситуация первая.

В жизни, часто встречаются ситуации, где отрицательные числа не имеют никакого практического смысла.

Например, мы не можем проехать на машине «минус 70 километров» (мы проедем 70 километров, неважно, в каком направлении), как и не можем купить «минус 5 кг апельсинов». Эти значения всегда должны быть положительными.

Именно для обозначения таких ситуаций математики придумали специальный термин – модуль или абсолютная величина.

Ситуация вторая.

Ты покупаешь пакет чипсов «Lay’s». На пакете написано, что он весит 100 грамм. Но если ты начнешь взвешивать пакеты, вряд ли они будут весить ровно 100 грамм. Какой-то из них будет весить 101 грамм, а какой-то 99.

И что, можно идти судиться с компанией Lays, если они тебе недовесили?

Нет. Потому что Lays устанавливает допуск и говорит, что пакет будет весить 100 грамм, плюс-минус 1 грамм. Вот это «плюс-минус» — это и есть модуль.

Ситуация третья.

В жизни вообще не бывает 100% точных величин. Всегда есть вот такие допуски. В зарплате, например: «Я согласен работать за 250 тыс рублей в месяц, плюс-минус 20 тыс!» 20 тысяч — это и есть модуль.

А вообще для простоты запомни, что модуль это расстояние от нуля в любую сторону.

Ну вот, ты уже почти все знаешь. Давай теперь подробнее.

Видео:Геометрия 7 класс (Урок№24 - Соотношения между сторонами и углами треугольника. Неравенство треуг.)Скачать

Что же такое модуль числа?

Представь, что это ты.

Предположим, что ты стоишь на месте и можешь двигаться как вперёд, так и назад. Обозначим точку отправления .

Итак, ты делаешь шага вперёд и оказываешься в точке с координатой .

Это означает, что ты удалился от места, где стоял на шага ( единичных отрезка). То есть, расстояние от начала движения до точки, где ты в итоге оказался, равно .
Но ведь ты же можешь двигаться и назад!

Если от отправной точки с координатой сделать шага в обратную сторону, то окажешься в точке с координатой .

Какое расстояние было пройдено в первом и во втором случае? Конечно же, расстояние, пройденное в первом и во втором случае, будет одинаковым и равным трем, ведь обе точки ( и ), в которых ты оказался одинаково удалены от точки, из которой было начато движение ( ).

Таким образом, мы приблизились к понятию модуля . Получается, что модуль показывает расстояние от любой точки на координатном отрезке до точки начала координат.

Так, модулем числа будет . Модуль числа также равен , потому что расстояние не может быть отрицательным !

Модуль – это абсолютная величина

Обозначается модуль просто:

Итак, найдём модуль числа и :

Видео:Как решить неравенства с модулем?Скачать

Основные свойства модуля

Вот мы и приблизились к первому свойству модуля:

Модуль не может быть выражен отрицательным числом.

То есть, если – число положительное, то его модуль будет равен этому же числу:

если ext mathbf ,»> то .

Если – отрицательное число, то его модуль равен противоположному числу:

А если ? Ну, конечно! Его модуль также равен :

Из этого следует, что модули противоположных чисел равны, то есть:

А теперь потренируйся:

Ответы: 9; 3; 16; 8; 17.

Довольно легко, правда?

А если перед тобой вот такое число:

Как быть здесь? Как раскрыть модуль в этом случае? Действуем по тому же сценарию.

Сначала определяем знак выражения под знаком модуля, а потом раскрываем модуль :

• если значение выражения больше нуля, то просто выносим его из-под знака модуля,
• если же выражение меньше нуля, то выносим его из-под знака модуля, меняя при этом знак, как делали это ранее в примерах.

Ну что, попробуем? Оценим :

Если , то какой знак имеет ? Ну конечно, !

А, значит, знак модуля раскрываем, меняя знак у выражения:

Разобрался? Тогда попробуй сам:

Какими же ещё свойствами обладает модуль?

Если нам нужно перемножить числа внутри знака модуля, мы спокойно можем перемножить модули этих чисел.

Выражаясь математическим языком, модуль произведения чисел равен произведению модулей этих чисел.

А что, если нам нужно разделить два числа (выражения) под знаком модуля?

Да то же, что и с умножением! Разобьем на два отдельных числа (выражения) под знаком модуля:

при условии, что (так как на ноль делить нельзя).

Стоит запомнить ещё одно свойство модуля:

Модуль суммы чисел всегда меньше или равен сумме модулей этих чисел:

Почему так? Всё очень просто!

Как мы помним, модуль всегда положителен. Но под знаком модуля может находиться любое число: как положительное, так и отрицательное. Допустим, что числа и оба положительные. Тогда левое выражение будет равно правому выражению.

Рассмотрим на примере:

Выражения также равны, если оба числа отрицательны:

Если же под знаком модуля одно число отрицательное, а другое положительно, левое выражение всегда окажется меньше правого:

Вроде с этим свойством все ясно, рассмотрим еще парочку полезных свойств модуля.

Что если перед нами такое выражение:

Что мы можем сделать с этим выражением? Значение x нам неизвестно, но зато мы уже знаем, что , а значит .

Число больше нуля, а значит можно просто записать:

Вот мы и пришли к другому свойству, которое в общем виде можно представить так:

А чему равно такое выражение:

Итак, нам необходимо определить знак под модулем. А надо ли здесь определять знак?

Конечно, нет, если помнишь, что любое число в квадрате всегда больше нуля! Если не помнишь, смотри тему степень и ее свойства. И что же получается? А вот что:

Здорово, да? Довольно удобно. А теперь конкретный пример для закрепления:

Ну, и почему сомнения? Действуем смело!

Во всем разобрался? Тогда вперед тренироваться на примерах!

1. Найдите значение выражения , если .

2. У каких чисел модуль равен ?

3. Найдите значение выражений:

Если не все пока ясно и есть затруднения в решениях, то давай разбираться:

Итак, подставим значения и в выражение

Как мы помним, противоположные числа по модулю равны. Значит, значение модуля, равное имеют два числа: и .

Все уловил? Тогда пора перейти к более сложному!

Попробуем упростить выражение

Итак, мы помним, что значение модуля не может быть меньше нуля. Если под знаком модуля число положительное, то мы просто можем отбросить знак: модуль числа будет равен этому числу.

Но если под знаком модуля отрицательное число, то значение модуля равно противоположному числу (то есть числу, взятому со знаком «–»).

Для того, чтобы найти модуль любого выражения, для начала нужно выяснить, положительное ли значение оно принимает, или отрицательное.

Получается, значение первого выражения под модулем .

, следовательно, выражение под знаком модуля отрицательно. Второе выражение под знаком модуля всегда положительно, так как мы складываем два положительных числа.

Итак, значение первого выражения под знаком модуля отрицательно, второго – положительно:

Это значит, раскрывая знак модуля первого выражения, мы должны взять это выражение со знаком «–». Вот так:

Во втором случае просто отбросим знак модуля:

Упростим данное выражение целиком:

Видео:Неравенство треугольникаСкачать

Модуль числа и его свойства (строгие определения и доказательства)

Модуль (абсолютная величина) числа — это само число , если , и число , если :

🌟 Видео

Как решать уравнения с модулем или Математический торт с кремом (часть 1) | МатематикаСкачать

Неравенства с модулем Часть 1 из 2 Простейшие неравенстваСкачать

Неравенство треугольника. Геометрия 7 класс. Доказательство. Задачи по рисункам.Скачать

НЕРАВЕНСТВА С МОДУЛЕМ 😉 ЧАСТЬ I #shorts #математика #егэ #огэ #профильныйегэСкачать

НЕРАВЕНСТВА С МОДУЛЕМСкачать

Неравенство треугольника | Геометрия 7-9 класс #34 | ИнфоурокСкачать

Неравенства с модулем. Как правильно раскрывать модульСкачать