Множество треугольников разбивается на классы

Математика | 10 — 11 классы

. Множество треугольников разбивается на классы, если из него выделяются подмножества треугольников : а) прямоугольных, равнобедренных, равносторонних ; б) остроугольных, тупоугольных, прямоугольных ; в) равносторонних, прямоугольных, тупоугольных.

Построй тупоугольный треугольник?

Построй тупоугольный треугольник.

Можно ли разбить построенный треугольник на два треугольника так, чтобы один из них был : а) прямоугольной?

Постройте треугольник?

Равнобедренный и остроугольный, ж).

Равнобедренный и тупоугольный.

Из множества треугольников выделены подмножества прямоугольных треугольников, равнобедренных треугольников и тупоугольных треугольников?

Из множества треугольников выделены подмножества прямоугольных треугольников, равнобедренных треугольников и тупоугольных треугольников.

Произошло ли разбиение множества на классы ?

На рисунке 125 изображены различные треугольники?

На рисунке 125 изображены различные треугольники.

Какая из этих треугольников являются равнобедренными?

Если среди них равносторонние треугольники?

Какие треугольники являются остроугольными?

Укажите равнобедренный треугольник , равнобедренный тупоугольный треугольник, равнобедренный остроугольный треугольник.

Помогите пожалуйста?

На рисунке изображены различные треугольники(цветные).

Какие из этих треугольников являются равнобедренным?

Если ли среди них равносторонние треугольники?

Какие треугольники являются остроугольными?

Укажите равнобедренный прямоугольный треугольник, равнобедренный тупоугольный треугольник, равнобедренный остроугольный треугольник.

Можно ли разбить построенный треугольник на два треугольника так чтобы один из них был прямоугольный остроугольный тупоугольный?

Можно ли разбить построенный треугольник на два треугольника так чтобы один из них был прямоугольный остроугольный тупоугольный.

Существует ли равносторонний тупоугольный треугольник?

Существует ли равносторонний тупоугольный треугольник?

Равносторонний прямоугольный треугольник?

На чертеже 12 треугольников?

На чертеже 12 треугольников.

Выпиши названия тупоугольных, прямоугольных и остроугольных треугольников.

Образец : Тупоугольные : ABC.

Какие из треугольников, изображённых на рисунке 7?

Какие из треугольников, изображённых на рисунке 7.

1, являются равнобедренными?

Есть ли среди них равносторонние треугольники?

Какие из данных треугольников являются остроугольными?

Назовите равнобедренный прямоугольный треугольник ; равнобедренный тупоугольный треугольник ; равнобедренный остроугольный треугольник.

ПЛИС ОЧЕНЬ СРОЧНО.

Остроугольный, тупоугольный и прямоугольный треугольник описание?

Остроугольный, тупоугольный и прямоугольный треугольник описание.

На этой странице находится вопрос . Множество треугольников разбивается на классы, если из него выделяются подмножества треугольников : а) прямоугольных, равнобедренных, равносторонних ; б) остроугольных, тупоугольных, прямоугольных ?, относящийся к категории Математика. По уровню сложности данный вопрос соответствует знаниям учащихся 10 — 11 классов. Здесь вы найдете правильный ответ, сможете обсудить и сверить свой вариант ответа с мнениями пользователями сайта. С помощью автоматического поиска на этой же странице можно найти похожие вопросы и ответы на них в категории Математика. Если ответы вызывают сомнение, сформулируйте вопрос иначе. Для этого нажмите кнопку вверху.

227 + 318 + (318 + 97) = 950 рабочии не справились.

Ответ Б) 3 / 4 * 3 = 9 / 4 = 2 1 / 4 и + 3 / 4 = 3.

А)500 — 250 = 250(тг) осталось у Амирхана б)250 + 250 = 500(тг) было всего у Амирхана в)500 — 250 = 250(тг) потратил Амирхан на подарок.

42 — 2 * 6 = 30(см) 2 стороны 30 : 2 = 15(см) длина 15 * 6 = 90(см)площадь прямоугольника 24 : 4 = 6(см) сторона квадрата 6 * 6 = 36(см) площадь квадрата 90>36.

17, 8 — 37 : 2 3 / 17 + 1 2 / 7 = 2 3 / 35, 1)37 : 2 3 / 17 = 37 : 37 / 17 = 37 * 17 / 37 = 17, 2) 17, 8 — 17 = 0, 8, 3) 0, 8 + 1 2 / 7 = 4 / 5 + 9 / 7 = 28 / 35 + 45 / 35 = 73 / 35 = 2 3 / 35.

В первый день посадили х деревьев, во второй день в 2 раза больше чем в первый, значит, 2х, а в третий х + 10. Х + 2х + (х + 10) = 210 ; 4х + 10 = 210 ; 4х = 210 — 10 = 200 ; х = 200 / 4 = 50 деревьев в первый день, во второй 2х = 2×50 = 100, и в тр..

1) 3, 5 — 2, 5 = 1 (км / ч) скорость лодки против течения 2) 3, 5 + 2, 5 = 6 (км / ч) скорость лодки по течению 3) 1 * 0, 4 = 0, 4 (км) проплыла лодка против течения 4) 6 * 0, 8 = 4, 8 (км) проплыла лодка по течению 5) 4, 8 + 0, 4 = 5, 2 (км) всего п..

1 + 3 + 5 + 7 + 9 + 11 и так далее до 100 считай дружок.

220 * 0, 6 = 132 дет. — 60% 220 — 132 = 88 дет. — записались в худ. 220 * 0, 35 = 77 — перешли. 88 + 77 = 154 — стало в худ.

1) 15 — 8 = 7 (карамелек) — стало у малыша 2)8 — 7 = 1 (карамелька) на столько меньше Ответ : у него стало на 1 карамелька больше.

Понятие разбиения множества на классы

Понятие множества и операций над множествами позволяют уточнить представление о классификации.

Классификация – это действие распределения объектов по классам на основании сходств внутри класса и их отличия от других объектов. Классификация широко применяется в математике.

Например, натуральные числа делятся на четные и нечетные; углы бывают острые, тупые и прямые и т.д.

Любая классификация связана с разбиением некоторого множества объектов на подмножества.

Считают, что множество Х разбито на классы Х, Х,…, Х, если:

1) подмножества Х, Х,…, Х попарно не пересекаются;

2) объединение этих подмножеств совпадает с множеством Х.

Если не выполнено хотя бы одно из этих условий, классификацию считают неправильной.

Например: а) Множество треугольников Х разбито на три класса: остроугольные, прямоугольные и тупоугольные. Действительно, выделенные подмножества попарно не пересекаются, а их объединение совпадает с множеством Х; b) Из множества треугольников Х выделили подмножества равнобедренных, равносторонних и разносторонних треугольников. Так как множества равнобедренных и равносторонних треугольников пересекаются, значит, не выполнено первое условие классификации, и разбиения множества Х на классы мы не получили.

Так как разбиение множества на классы связано с выделением его подмножеств, то классификацию можно выполнять при помощи свойств элементов множеств.

Рассмотрим, например, множество натуральных чисел. Его элементы обладают различными свойствами. Нас интересуют числа со свойством «быть кратным 3». Это свойство позволяет выделить из множества N подмножество, состоящее из чисел, кратных 3. Тогда про остальные натуральные числа можно сказать, что они не кратны 3, т.е. получаем еще одно подмножество множества N. Так как выделенные подмножества не пересекаются, а их объединение совпадает с множеством N, то имеем разбиение данного множества на два класса.

Вообще, если на множестве Х задано одно свойство, то это множество разбивается на два класса. Первый – это класс объектов, обладающих данным свойством, а второй – дополнение первого класса до множества Х. Во втором классе содержатся такие объекты множества Х, которые заданным свойством не обладают. Такую классификацию называют дихотомической.

Рассмотрим ситуацию, когда для элементов множества заданы два свойства. Например, свойства натуральных чисел: «быть кратным 3» и «быть кратным 5». При помощи этих свойств из множества N можно выделить два подмножества: А – множество чисел, кратных 3 и В – множество чисел, кратных 5. Эти множества пересекаются, но ни одно из них не является подмножеством другого (рис. 13). Разбиения на подмножества А и В в данном случае на произошло. Но круг, изображающий множество N, можно рассматривать как состоящий из четырех непересекающихся областей. Каждая область изображает некоторое подмножество множество N. Множество I состоит из чисел, кратных 3 и 5, множество I – из чисел, кратных 3 и не кратных 5, множество III – из чисел, кратных 5 и не кратных 3, множество IV – из чисел, не кратных 3 и не кратных 5. Объединение этих четырех множеств есть множество N.

Таким образом, выделение двух свойств привело к разбиению множества N натуральных чисел на четыре класса.

Не следует думать, что задание двух свойств элементов множества всегда приводит к разбиению этого множества на четыре класса. Например, при помощи таких двух свойств «быть кратным 3» и «быть кратным 6» множество натуральных чисел разбивается

на три класса (рис. 14): I – класс чисел, кратных 6; II – класс чисел, кратных 3, но не кратных 6; III – класс чисел, не кратных 3.

Понятие разбиения множества на классы

Дата добавления: 2014-09-06 ; просмотров: 8142 ; Нарушение авторских прав

Понятие множества и операций над множествами позволяют уточнить наше представление о классификации.

Любая классификация связана с разбиением некоторого множества объектов на подмножества.

3) объединение подмножеств совпадает с множеством А.

Если не выполнено хотя бы одно свойство, то классификацию считают неправильной.

Например, если множество треугольников разбить на остроугольные, прямоугольные и тупоугольные, то разбиение будет выполнено верно, т.к. выполнены все условия, данные в определении.

Если из множества треугольников выделить подмножества равносторонних, равнобедренных и разносторонних треугольников, то разбиения мы не получим, т.к. множество равносторонних треугольников является подмножеством равнобедренных треугольников, т.е. не выполняется второе условие разбиения множества на классы.

Пример 1. Пусть А – множество двузначных чисел. Рассмотрим на этом множестве свойство «быть четным».

А

Множество А разбилось на два подмножества:

А₁ – множество четных чисел,

А₂ – множество нечетных чисел, при этом

Т.о. задание одного свойства приводит к разбиению этого множества на 2 класса.

Пример 2. Пусть А – множество треугольников. Рассмотрим на данном множестве два свойства: «быть прямоугольным» и «быть равнобедренным». При помощи этих свойств из множества треугольников можно выделить 2 подмножества: В – множество прямоугольных треугольников и С – множество равнобедренных треугольников. Эти множества пересекаются, но ни одно из них не является подмножеством другого.

По рисунку видно, что получилось 4 класса:

I – В Ç С – множество равнобедренных прямоугольных треугольников;

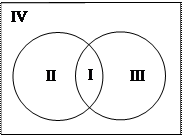
II – В Ç 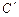– множество прямоугольных, но не равнобедренных треугольников;

III – 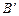Ç С – множество равнобедренных, но не прямоугольных треугольников;

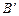
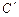
IV – Ç – множество не равнобедренных и не прямоугольных треугольников.

Т.о. с помощью двух свойств множество разбилось на 4 класса, таких, что их пересечение пусто, а их объединение составляет множество А.

Следует отметить, что задание двух свойств приводит к разбиению множества на 4 класса не всегда.

Пример 3. Пусть А – множество треугольников. Рассмотрим на данном множестве два свойства: «быть прямоугольным» и «быть остроугольным». При помощи этих свойств из множества треугольников можно выделить 2 подмножества: В – множество прямоугольных треугольников и С – множество остроугольных треугольников. Эти множества не пересекаются. По рисунку видно, что при помощи этих свойств множество треугольников разбивается на три класса:

I – множество прямоугольных треугольников;

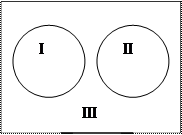
II – множество остроугольных треугольников;

III – множество не прямоугольных, не остроугольных треугольников.

Контрольные вопросы

1. При каких условиях считают, что множество разбито на классы?

2. Как определить число элементов в объединении двух или трех конечных множеств?