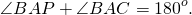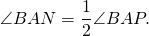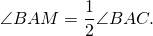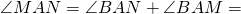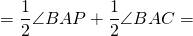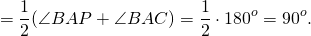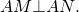Биссектриса внешнего угла треугольника

В данной публикации мы рассмотрим определение и основные свойства биссектрисы угла треугольника, а также приведем пример решения задачи, чтобы закрепить представленный материал.

Видео:Свойство биссектрисы внешнего угла треугольникаСкачать

Определение биссектрисы угла треугольника

Биссектриса угла – это луч, который берет начала в вершине угла и делит данный угол пополам.

Биссектриса треугольника – это отрезок, соединяющий вершину угла треугольника с противоположной стороной и делящий этот угол на две равные части. Такая биссектриса, также, называется внутренней.

Основание биссектрисы – точка на стороне треугольника, которую пересекает биссектриса. Т.е. в нашем случае – это точка D.

Внешней называется биссектриса угла, смежного с внутренним углом треугольника.

Видео:Теорема о свойстве биссектрисы внешнего угла треугольника ДоказательствоСкачать

Свойства биссектрисы треугольника

Свойство 1 (теорема о биссектрисе)

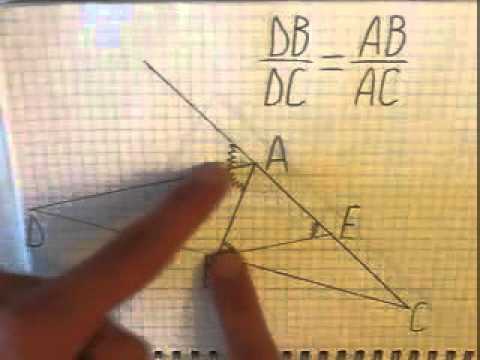
Биссектриса угла треугольника делит его противоположную сторону в пропорции, равной отношению прилежащих к данному углу сторон. Т.е. для нашего треугольника (см. самый верхний рисунок):

Свойство 2

Точка пересечения трех внутренних биссектрис любого треугольника (называется инцентром) является центром вписанной в фигуру окружности.

Свойство 3

Все биссектрисы треугольника в точке пересечения делятся в отношении, равном сумме прилежащих к углу сторон, деленной на противолежащую сторону (считая от вершины).

Свойство 4

Если известны длины отрезков, образованных на стороне, которую пересекает биссектриса, а также две другие стороны треугольника, найти длину биссектрисы можно по формуле ниже (следует из теоремы Стюарта):

BD 2 = AB ⋅ BC – AD ⋅ DC

Свойство 5

Внешняя и внутренняя биссектрисы одного и того же угла треугольника перпендикулярны друг к другу.

• CD – внутренняя биссектриса ∠ACB;
• CE – биссектриса угла, смежного с ∠ACB;
• ∠DCE равен 90°, т.е. биссектрисы CD и CE перпендикулярны.

Видео:№242. Докажите, что если биссектриса внешнего угла треугольника параллельна стороне треугольника,Скачать

Пример задачи

Дан прямоугольный треугольник с катетами 6 см и 8 см. Найдите длину биссектрисы, проведенной к гипотенузе.

Решение
Нарисуем чертеж согласно условиям задачи.

Применив теорему Пифагора мы можем найти длину гипотенузы (ее квадрат равен сумме квадратов двух катетов).
BC 2 = AB 2 + AC 2 = 6 2 + 8 2 = 100.
Следовательно, BC = 10 см.

Далее составляем пропорцию согласно Свойству 1, условно приняв отрезок BD на гипотенузе за “a” (тогда DC = “10-a”):

Избавляемся от дробей и решаем получившееся уравнение:
8a = 60 – 6a
14a = 60
a ≈ 4,29

Таким образом, BD ≈ 4,29 см, CD ≈ 10 – 4,29 ≈ 5,71 см.

Теперь мы можем вычислить длину биссектрисы, использую формулу, приведенную в Свойстве 4:
AD 2 = AB ⋅ AC – BD ⋅ DC = 6 ⋅ 8 – 4,29 ⋅ 5,71 ≈ 23,5.

Видео:Внешний угол треугольникаСкачать

Биссектриса внешнего угла треугольника

Чему равен угол, который образует биссектриса внешнего угла треугольника с биссектрисой смежного ему внутреннего угла?

Биссектриса внешнего угла треугольника перпендикулярна биссектрисе смежного с ним внутреннего угла.

Дано: ∆ ABC,

∠BAP — внешний угол при вершине A,

AN — биссектриса ∠BAP,

AM — биссектриса ∠BAC.

Доказательство: (аналогично доказательству об угле между биссектрисами смежных углов).

Так как внешний угол треугольника — это угол, смежный с внутренним углом при данной вершине, то по свойству смежных углов

Так как AN — биссектриса внешнего угла BAP, то

Так как AM — биссектриса угла BAC, то

Итак, мы доказали, что биссектриса внешнего угла треугольника образует с биссектрисой внутреннего угла при данной вершине прямой угол:

Вывод: если требуется найти угол между биссектрисами внешнего и внутреннего углов треугольника, знать градусные меры самих углов не требуется. Каким бы ни был внешний угол треугольника, его биссектриса перпендикулярна биссектрисе смежного внутреннего угла.

Видео:57 Длина биссектрисы внешнего углаСкачать

4 Comments

докажите что биссектриса внешнего угла противоположного основанию равнобедренного треугольника параллельна основатию этого угла

Решите пожалуйста. Один из углов треугольника равен альфа. Найдите угол между биссектрисами внешних углов, проведённых из вершин двух других углов.

Видео:Задача про биссектрису внешнего угла ждёт тебя на ЕГЭ-2022. Геометрические конструкции.Скачать

Биссектриса треугольника онлайн

С помощю этого онлайн калькулятора можно найти биссектрису треугольника. Для нахождения длины биссектрисы треугольника введите длины сторон треугольника, выберите сторону, к которой проведена биссектриса и нажмите на кнопку «Вычислить». Теоретическую часть смотрите ниже.

Определение 1. Отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны называется биссектрисой треугольника (Рис.1).

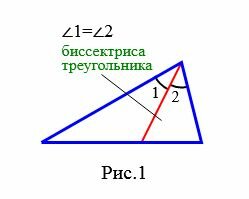Биссектриса треугольника также называют биссектрисей угла треугольника или биссектрисей внутреннего угла треугольника.

Биссектриса внешнего угла треугольника − это биссектриса угла, которая является смежным с внутренним углом треугольника (Рис.2).

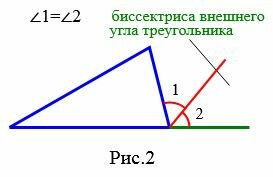Любой треугольник имеет три биссектрисы.

Теорема 1. Биссектрисы треугольника пересекаются в одной точке.

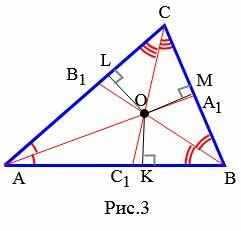Доказательство. Проведем биссектрисы AA₁, BB₁ и обозначим через O точку их пересечения (Рис.3). Из точки O проведем перпендикуляры OK, OM и OL по сторонам треугольника ABC. По теореме 1 статьи Биссектриса угла. Свойства − OK=OL OK=OM. Следовательно OL=OM. Но последнее равенство означает, что точка O равноудалена от сторон AC и BC, т.е. находится на биссектрисе CC₁ (Определение 2 статьи Биссектриса угла. Свойства).

Точка пересечения биссектрис треугольника называется инцентром треугольника. Инцентр треугольника является центром вписанной в треугольник окружности (Рис.4).

Доказательство следует из теоремы 1, поскольку точка O равноудалена от сторон треугольника ABC и, следовательно, является центром окружности равной OK=OL=OM.

Видео:Свойство (признак) биссектрисы внутреннего (внешнего) угла треугольникаСкачать

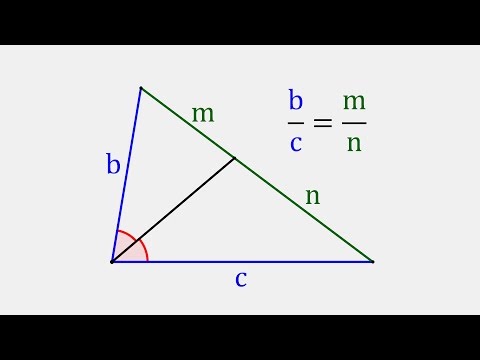
Длина биссектрисы треугольника

Рассмотрим треугольник на Рис.5.

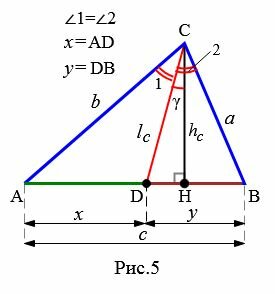Длина биссектрисы треугольника можно вычислить следующими формулами:

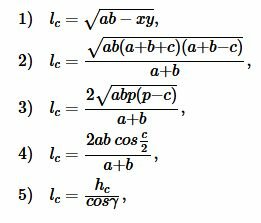где p − полупериметр треугольника ABC, ( small gamma -) угол между биссектрисой ( small l_c) и вершиной ( small h_c:)

,

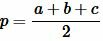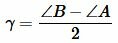Доказательство. 1) Из теоремы Стюарта следует:

(1)

А из теоремы о биссектрисе треугольника следует, что если l_c является биссектрисей треугольника ABC (Рис.5), то имеет место следующее соотношение:

(2)

Поскольку 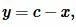то (2) можно переписать так:

(3)

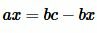(4)

(5)

Подставим (4) и (5) в (1):

.

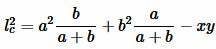(6)

.

Доказательство. 2) Подставим (4) и (5) в (6):

,

.

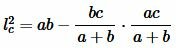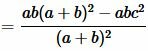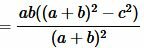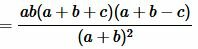(7)

.

(8)

Доказательство. 3) Сделаем следующее обозначение:

.

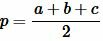(9)

Сделаем преобразования формулы (7), учитывая (9):

.

.

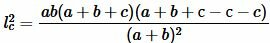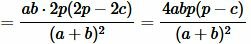(10)

Доказательство. 4) Для доказательства четвертой формулы, снова обратимся к рисунке Рис.5. Запишем формулы площадей треугольников ABC, ADC и BDC:

,

,

.

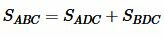
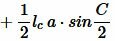Учитывая, что , получим:

.

.

(11)

Для ( small sin C ) применим формулу синуса двойного угла:

.

(12)

Подставляя (12) в (11) получим:

.

.

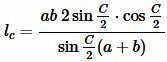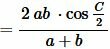(13)

Доказательство. 5) Докажем пятую формулу. Из вершины C проведена вершина CH. Имеем прямоугольный треугольник CHD, для которого имеет место следующее равенство:

.

.

Остается показать, что .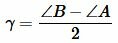

Поскольку биссектриса l_c делит угол C пополам, то:

🔍 Видео

№233. Докажите, что биссектриса внешнего угла при вершине равнобедренного треугольника,Скачать

Теорема о биссектрисе угла треугольника | Осторожно, спойлер! | Борис Трушин |Скачать

3 свойства биссектрисы #shortsСкачать

№677. Биссектрисы внешних углов при вершинах В и С треугольника ABC пересекаются в точке ОСкачать

ХОЗБЛОК. Армокаркас для ленточного фундамента 4м * 3 м.Скачать

№259. Угол, противолежащий основанию равнобедренного треугольника, равен 120°. Высота, проведеннаяСкачать

Длина отрезка биссектрисы внешнего угла треугольникаСкачать

Геометрия 7 класс (Урок№12 - Медианы треугольника. Биссектрисы треугольника. Высоты треугольника.)Скачать

8 класс, 35 урок, Свойства биссектрисы углаСкачать

Сумма углов треугольника. Геометрия 7 класс | МатематикаСкачать

Отделка внутренних и внешних углов под покраску. ПЕРЕДЕЛКА ХРУЩЕВКИ от А до Я #19Скачать

Внешний угол треугольникаСкачать

Теперь ты будешь находить углы за секунды. Как найти внешний угол треугольника? #математика #углыСкачать