Наполеон теорема о треугольниках

Видео:Математика это не ИсламСкачать

Теорема Наполеона, и не только

Известно, что Наполеон Бонапарт (1769–1821) увлекался математикой, больше всего – геометрией. В частности, известен его способ деления окружности на четыре равные части с помощью только циркуля. Будучи политическим деятелем, Наполеон всегда высоко ставил роль науки и учёных в строительстве государственности. Так о математике он говорил:

Процветание и совершенство математики тесно связаны с благосостоянием государства.

Как-то Наполеон, который тогда еще не был правителем Франции, спорил с известными математиками Лагранжем и Лапласом. Во время одной из дискуссий Лаплас прервал Наполеона словами:

Меньше всего мы желаем, чтоб вы, генерал, учили нас геометрии!

Интересно, что в дальнейшем Лаплас стал главным военным министром Наполеона.

Теорема Наполеона

Теорема, о которой пойдёт речь впервые была опубликована английским математиком Уильямом Резерфордом (1798–1871) в 1825 году, спустя 4 года после смерти Наполеона. Хотя Наполеон и занимался геометрией достаточно серьёзно и небезуспешно, как для непрофессионального математика, многие специалисты сомневаются в том, что он является автором теоремы, названной его именем. А теперь к сути.

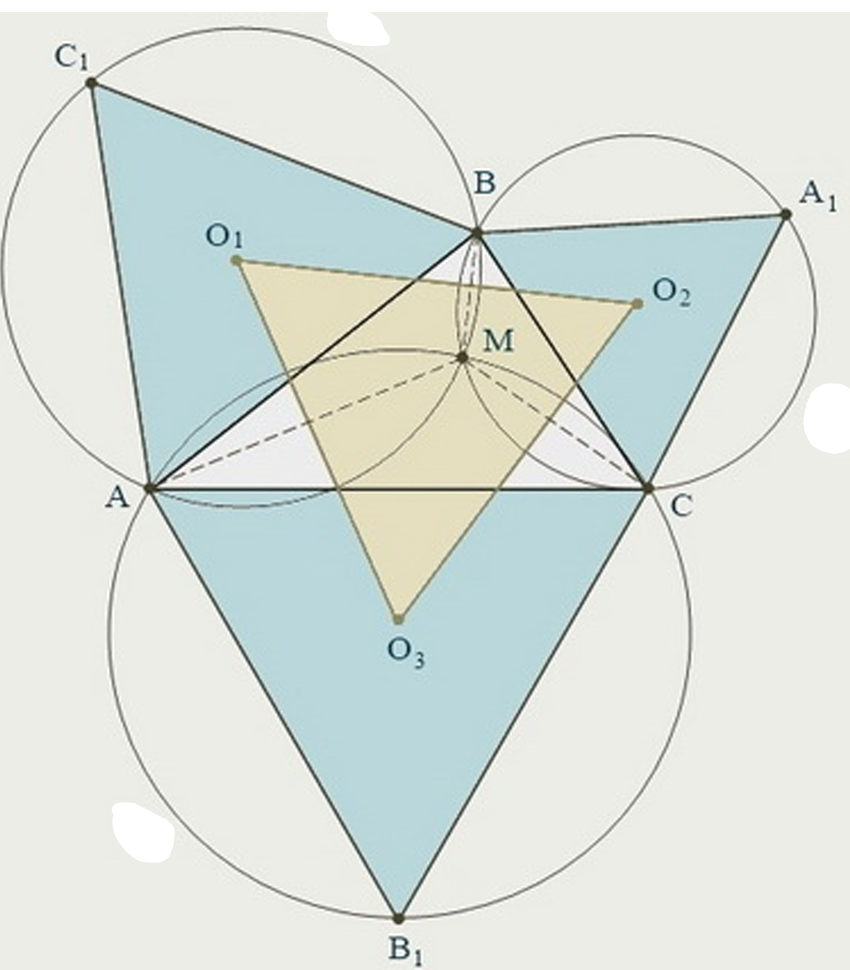
Если на сторонах треугольника построить правильные треугольники, то получим конфигурацию из четырех треугольников, которую называют треугольниками Наполеона . Окружности, описанные вокруг построенных правильных треугольников, называют окружностями Торричелли .

Именно Наполеону Бонапарту – императору Франции и великому полководцу – история приписывает изучение этой конфигурации, формулировку и доказательство утверждения, известного как теорема Наполеона :

Если на сторонах произвольного треугольника извне его построены равносторонние треугольники, то их центры являются вершинами равностороннего треугольника .

В различных источниках приводятся разные доказательства теоремы Наполеона. Чаще всего можно встретить доказательства, основанные на свойствах поворота или использующие комплексные числа. С одним из элементарных доказательств, основанном на применении теоремы косинусов, можно познакомиться на сайте «Математика, которая мне нравится». Мы докажем теорему Наполеона, используя свойства окружности.

Пусть на сторонах треугольника АВС построены равносторонние треугольники АВС ₁, А ₁ ВС и АВ ₁ С ; ω ₁, ω ₂ и ω ₃ – окружности, описаны вокруг этих треугольников (соответственно). Докажем, что ω ₁, ω ₂ и ω ₃ пересекаются в одной точке – точке Торричелли .

Обозначим точку пересечения окружностей, описанных вокруг треугольников А ₁ ВС и АВ ₁ С , как М . Тогда

∠АМС = 180° – 60° = ∠ВМС .

∠АМВ = 360° – 2 · 120° = 120°,

и точка М лежит на окружности, описанной вокруг АВС ₁. Прямые О ₁ О ₃ и О ₁ О ₂ перпендикулярны к общим хор­дам АМ и ВМ окружностей ω ₁ и ω ₃, ω ₁ и ω ₂ соответственно.

Аналогично: ∠О ₂ = ∠О ₃ = 60°, и треугольник О ₁ О ₂ О ₃ – правильный. Теорема Наполеона доказана.

Мы строили правильные треугольники извне заданного треугольника на его сторонах. Их ещё называют внешними треугольниками Наполеона для заданного треугольника. По аналогии, если правильные треугольники строят на сторонах треугольника внутрь его, то их называют внутренними треугольниками Наполеона для заданного треугольника. Треугольник с вершинами в центрах внутренних треугольников Наполеона также является правильным.

Теорема Петра-Дугласа-Неймана

Теорема Наполеона обобщается на случай произвольных треугольников теоремой Петра-Дугласа-Неймана :

Если подобные треугольники любой формы построены на сторонах треугольника внешним образом так, что каждый повёрнут относительно предыдущего, и три соответствующие точки этих треугольников соединены, то итоговый треугольник будет подобен этим внешним треугольникам.

Первая теорема Тебо

Аналогом теоремы Наполеона для параллелограммов является утверждение называемое первой теоремой Тебо :

Центры квадратов, построенных на сторонах параллелограмма, лежат в вершинах квадрата.

Теорема ван Обеля

Следует, пожалуй, упомянуть ещё один математический факт, опубликованный фламандским математиком ван Обелем (Henricus Hubertus van Aubel) в 1878 году, из которого теорема Тебо следует естественным образом:

Если на сторонах произвольного несамопересекающегося четырёхугольника построить квадраты внешним образом и соединить центры противоположных, то полученные отрезки будут равны и перпендикулярны.

Источники: Г.В. Апостолова. Геометрия 8 (Киев, «Генеза», 2008), Википедия.

Видео:#218. ТЕОРЕМА НАПОЛЕОНАСкачать

Император науки

Н аполеон I Бонапарт родился 15 августа 1769 года. Все вспоминают о Наполеоне как о французском императоре, покорившем всю Европу, но споткнувшемся на России, как о великом государственном деятеле и великом полководце. Но редко кто вспоминает о Наполеоне как покровителе наук и искусств и как об ученом, который был избран в 1797 году членом Института Франции по отделению физико-математических наук, секции механики. Институт Франции заменил после революции все существовавшие до этого академии наук и искусств. Выборы прошли в обстановке жесткой конкуренции, у Наполеона было 11 соперников. Причем не надо думать, что «бессмертные» испугались гнева боевого генерала. Нет. Наполеон отметился реальным достижением в области математики — доказательством теоремы, получившей его имя: если на каждой стороне произвольного треугольника построить по равностороннему треугольнику, то треугольник с вершинами в центрах равносторонних треугольников — тоже равносторонний. Возможно, кому-то эта теорема покажется недостаточно серьезной для звания академика, но сам Наполеон гордился своими научными достижениями не меньше чем военными и неоднократно подчеркивал, что он с учеными «одной крови».

Пусть ABC — произвольный треугольник, и пусть на его сторонах построены равносторонние треугольники AC₁B, BA₁C и CB₁A (точки C₁, A₁ и B₁ лежат вне треугольника ABC). Тогда центры равносторонних треугольников AC₁B, BA₁C и CB₁A являются вершинами равностороннего треугольника.

Лемма. Окружности, описанные около треугольников AC₁B, BA₁C и CB₁A, пересекаются в одной точке.

Доказательство леммы. Пусть M — точка пересечения окружностей, описанных около треугольников BA₁C и CB₁A. Предположим, что точка M лежит внутри треугольника ABC (другие случаи оставляются читателям в качестве упражнения). Тогда из свойства вписанного четырехугольника вытекает, что углы BMC и CMA равны 120 градусам. Следовательно, угол AMB также равен 120 градусам, и точка P лежит также на окружности. описанной около треугольника ABC₁.

Доказательство теоремы. Обозначим через O₁, O₂ и O₃ центры равносторонних треугольников AC₁B, BA₁C и CB₁A соответственно. Как известно, прямая, соединяющая центры пересекающихся окружностей, перпендикулярна их общей хорде. Отсюда следует, что O₁O₂ перпендикулярно BM, O₂O₃ перпендикулярно CM и O₃O₁ перпендикулярно AM. В доказательстве леммы мы установили, что углы AMB, BMC и CMA равны 120 градусам (в случае, если точка M лежит внутри треугольника ABC; в противном случае нужно рассуждать чуть-чуть по-другому). По свойству углов с перпендикулярными сторонами отсюда вытекает, что углы O₁O₂O₃, O₂O₃O₁ и O₃O₁O₂ равны шестидесяти градусам, что и требовалось доказать.

(доказательство, взято из книги Г.С.М.Коксетера и С.Л.Грейтцера «Новые встречи с геометрией» (М., «Наука», 1978)

Бонапарт как-то написал: «Наука, которая открыла нам столько тайн и уничтожила столько предрассудков, призвана, чтобы оказать нам еще большие услуги; новые истины, новые открытия обнаружат нам тайны, еще более существенные для блага человечества, но необходимо, чтобы мы любили ученых и чтобы мы покровительствовали науке». Он сохранил это уважение на всю жизнь и требовал уважительного отношения к науке и от других.

Неосведомленность, некомпетентность в научных вопросах, тем более невежество были в его глазах непростительным пороком. Однажды Бернарден де Сен-Пьер, автор «Поля и Виржинии», прославленный писатель, чей талант Наполеон высоко ценил, пожаловался Бонапарту на то, что в Институте Франции, членами которого они оба состояли, к нему относятся без должного уважения. Наполеон на минуту задумался. «Скажите, — спросил он после недолгой паузы, — а вы знакомы с дифференциальным исчислением?» «Нет!» — чистосердечно признался писатель. «Так что же вы жалуетесь?!»

Наполеон на минуту задумался. «Скажите, — спросил он после недолгой паузы, — а вы знакомы с дифференциальным исчислением?» «Нет!» — чистосердечно признался писатель. «Так что же вы жалуетесь?!»

Ламартин позднее писал, что во времена Наполеона «только цифрам все разрешали, только цифры чествовались, осыпались благами и награждались».

При этом надо признать, что интерес Наполеона к науке был продолжением тенденции, которая началась в эпоху Просвещения и процветала во время Французской революции, которую поддержали многие ученые. А некоторые из них, как, например, Карно, сыграли большую роль в самые острые моменты революции.

Даже изгнанный на остров Святой Елены, Наполеон не оставил своего увлечения наукой и занялся изучением книг по физике, естественной истории, астрономии и химии.

Видео:Теорема НаполеонаСкачать

Будущий математик и его друзья

Семья будущего императора, проживавшая на Корсике, была небогата и многодетна, и Карло Буонапарте, стремясь дать сыновьям образование, не отягощая скудный семейный бюджет, отвез двух старших — Жозефа и Наполеона — в декабре 1778 года во Францию. Здесь не без хлопот он сумел их определить на казенный кошт.

Наполеон был помещен на стипендию в Бриеннское военное училище. Он пробыл в Бриенне пять лет. В училище Бонапарт обнаружил исключительные способности к математике, оставаясь всегда в этом предмете первым. Он показал отличные успехи по истории, географии и по другим дисциплинам, кроме латыни и немецкого: к языкам у него не было склонности. В 1784 году в октябре его перевели в Парижскую военную школу, помещавшуюся тогда на Марсовом поле.

Парижская военная школа справедливо считалась одной из лучших в стране, поскольку она располагала знающими, опытными преподавателями. Будущий император заслужил лестные отзывы почти всех своих преподавателей. Он специализировался в области артиллерии и, успешно сдав экзамены, в 1785 году был выпущен из училища в звании младшего лейтенанта.

Несколько человек, с которыми он познакомился в училище, стали впоследствии его друзьями, в том числе Гаспар Монж (отец начертательной геометрии), чей брат обучал Бонапарта математике Лапласа, а сам Лаплас был его экзаменатором

Несколько человек, с которыми он познакомился в училище, стали впоследствии его друзьями, в том числе Гаспар Монж (отец начертательной геометрии), чей брат обучал Бонапарта математике Лапласа, а сам Лаплас был его экзаменатором. Химика Бертолле молодой генерал встретил во время итальянской кампании в 1796 году. Все трое поддержали прием Наполеона в Институт Франции. Наполеон тоже не забывал о них: Монжа он назначил директором ведущего инженерного вуза Франции, созданного в годы революции, — Ecole polytechnique, членом сената, а потом и председателем сената, а Лапласа наградил титулом графа империи и всеми мыслимыми орденами и должностями. Он даже пробовал его на посту министра внутренних дел, но спустя шесть недель предпочел признать свою ошибку. Лаплас внес в управление, как выразился позднее Наполеон, «дух бесконечно малых», то есть мелочность. Впрочем, взамен утраченной должности министра Наполеон назначил Лапласа сенатором, так же как Бертолле.

Уже став первым консулом, Наполеон находит время, чтобы прочесть «Небесную механику» Лапласа, которую ученый посвятил ему.

Видео:49 Теорема НаполеонаСкачать

Не только математика

Все его товарищи по училищу вспоминали, как Бонапарт с удивительной для его возраста способностью часами просиживать за книгами достиг безусловного превосходства над ними в знаниях.

Записи, конспекты прочитанного, черновые заметки Наполеона остаются до сих пор наиболее убедительным доказательством его настойчивых усилий овладеть знаниями его времени, встать на уровень проблем века.

Философия, особенно просветительская, была для него ненавистной «идеологией»; политическую экономию он считал шарлатанством (особенно учение физиократов); философа Канта он тоже считал шарлатаном

Несколько тетрадей, исписанных его мелким почерком, — это конспекты книг и заметки, посвященные проблемам артиллерии, например обширная рукопись «Принципы артиллерии», и тетрадь с записями по истории артиллерии, и «Записка о способе расположения пушек при бомбометании» с математическими расчетами.

Но биографы отмечают также наряду со склонностью к математике исключительный интерес, более того — пристрастие молодого Бонапарта к истории.

Длительное и глубокое изучение истории и других общественных наук оказало большое влияние на развитие Бонапарта. Его выступления почти всегда содержат ссылки на исторические примеры, исторические факты, исторические имена. Известно, что во время обсуждения проекта Гражданского кодекса, ныне известного под его именем, он поражал членов комиссии, готовившей кодекс, цитируя древнеримских авторов на латыни.

Это не помешало Наполеону в 1803 году закрыть отделение «моральных и политических наук» Института Франции. Для него, бывшего поклонника Руссо, философы и моралисты стали вредными теоретиками. Философия, особенно просветительская, была для него ненавистной «идеологией»; политическую экономию он считал шарлатанством (особенно учение физиократов); философа Канта тоже считал шарлатаном. Как настоящий император, он писал: «Об общественных делах, являющихся моими собственными делами, в политической, социальной и моральной области, об истории, а именно современной истории, никто в настоящем поколении не будет думать, кроме меня, а в будущем поколении все будут думать так, как я».

От науки он требовал реальных результатов. Он хотел прежде всего, чтобы наука способствовала «славе империи» (он это высказал в письме к Лапласу в июле 1812 года из Витебска). Тогда даже такие абстрактные науки, как астрономия, тоже могут пригодиться. Преподавание в университете и в средней школе при нем имело утилитарный, преимущественно технический уклон.

Видео:Геометрия. 7 класс. Теоремы. Т5. Первое свойство равнобедренного треугольника.Скачать

Египетский поход

В 1798 году Наполеон во главе 54-тысячной армии высадился в Египте. Однако это вторжение имело и отчетливую научную составляющую. Как писал один из историков этого похода, «помимо солдат и матросов Наполеон привез 150 ученых и инженеров, чья ответственность заключалась в изучении египетской культуры и истории». Этот поход стал серьезным вкладом в развитие египтологии и не только.

Известен эпизод, случившийся во время египетского похода. Перед сражением у Александрии Наполеон построил свою армию в каре, в середине которого расположил ученых, сопровождавших армию, и вьючных животных. Приказ на этот счет звучал так: «Армию — в каре. Ослов и ученых в середину». Но это была не издевка, это было лапидарно сформулированное проявление заботы.

Еще когда «египетская кампания» обсуждалась в тогдашнем правительстве Франции — Директории, Бонапарт начал набирать лучших французских ученых того времени и сумел убедить многих сопровождать его в Египет. В ходе похода Наполеон регулярно встречался с руководителями научной экспедиции и всячески им помогал.

Монж, Бертолле и Магаллон выступили в качестве создателей и администраторов учрежденного во время похода Института Египта, который занимался не только египтологией, но и текущими заботами армии. Институт направил инженеров и географов для работы над проектами немедленного использования, такими как составление карты масштаба 1/30 000 Египта. Николя-Жак Конт создал завод по производству материалов для военной формы Франции. Гаспар Монж исследовал канал, построенный римлянами и связывающий Красное море с рекой Нил. Другие ученые больше сосредоточились на египетской цивилизации, изучая, например, недавно обнаруженный Розеттский камень. После ухода Бонапарта Институт Египта продолжал функционировать вплоть до прибытия в Египет британцев. Ученые вернулись во Францию в 1801 году с обширным набором заметок и рисунков о египетской культуре, истории, древности и естественной истории. Результатом их исследований была 23-томная энциклопедия Египта.

Видео:Теорема Пифагора. 8 КЛАСС | Математика | TutorOnlineСкачать

Преобразования науки и образования

Несмотря на строгий политический контроль, интеллектуальная жизнь при Наполеоне процветала, но во многом в соответствии с его видением роли науки носила утилитарный характер.

Хотя фундаментальные исследования тоже были на подъеме. Например, Бертолле опубликовал работу Essai de statique chimique (1803), в которой развивал теорию химического сродства Ньютона. Гей-Люссак вывел законы расширения объемов газов, а Ламарк предположил теорию эволюции, которую позже развил Дарвин.

«Все гениальные люди, все, кто занял почетное место на поприще науки, суть французы, какова бы ни была та страна, где они родились. Все те, кто пожелает отправиться во Францию, будут приняты правительством с отличием.»

Особенно Наполеон покровительствовал шести основным естественным дисциплинам: ботанике, химии, геологии, математике, физике и зоологии. Как первый консул он учредил несколько наград и денежных призов за научные достижения, в частности за работы в области электричества. Первым ею был награжден итальянский ученый Вольта в связи с его визитом в Париж для чтения лекций по электричеству в Институте Франции. Награды отражали повестку дня Наполеона в области наук и технологий.

Наполеон готов был приглашать во Францию ученых со всего света. Еще во время Итальянского похода тогда еще генерал Бонапарт писал итальянскому астроному Ориани: «Все гениальные люди, все, кто занял почетное место на поприще науки, суть французы, какова бы ни была та страна, где они родились. Все те, кто пожелает отправиться во Францию, будут приняты правительством с отличием. Французский народ придает большую цену приобретению ученого-математика, известного живописца, всякого выдающегося человека, в какой бы области он ни работал, нежели богатого и многолюдного города».

Обещанным премиям дана была невиданная по тем временам реклама. Сначала о них объявили в институте, где была образована по такому случаю комиссия, включавшая Лапласа, Кулона, Био. Размеры призов были оглашены под звуки фанфар. Позднее объявления о премиях были опубликованы в газетах и журналах. Поскольку премии по тем временам были колоссальные, большое число ученых, ранее пренебрегавших электричеством, сейчас стали усиленно работать в этой области. Тотчас же по личному распоряжению Наполеона в Политехнической школе была изготовлена целая батарея вольтовых столбов самых различных размеров, в том числе рекордный по величине столб, состоявший из 600 пар квадратных цинковых и медных пластин.

После 1807 года Бонапарт установил «Континентальную блокаду» Британии, Британия приняла ответные меры и отрезала пути доставки во Францию, в частности, тростникового сахара. Бонапарт назначил большие премии ученым, работавшим над получением сахара из свеклы, и задача была решена.

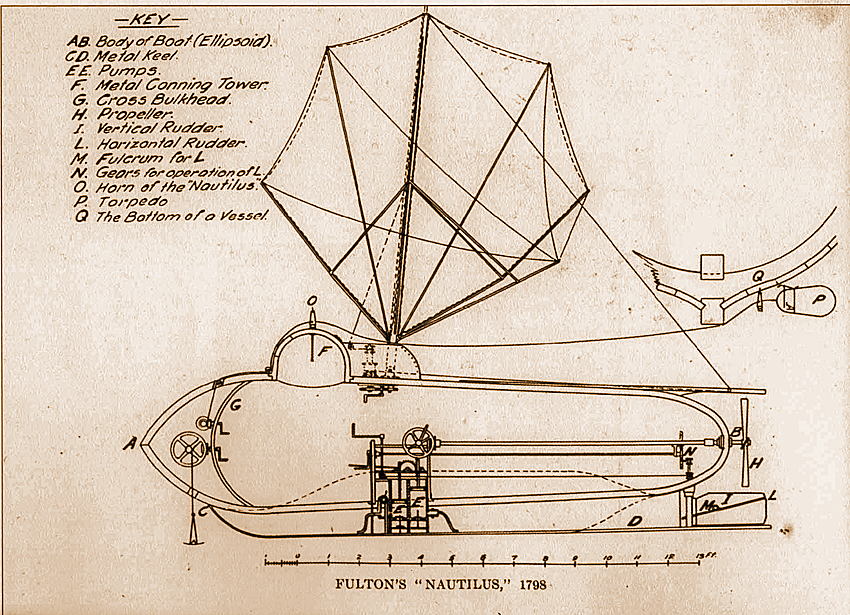
Это не означает, что все ученые и изобретатели имели успех у Наполеона. Американец Роберт Фултон пытался привлечь интерес Наполеона к своей подводной лодке «Наутилус» (которую он испытал на реке Сене в 1800 году), а затем к пароходу (1803 год). Несмотря на то что он получил правительственный грант, после испытаний последовал отказ от поддержки его со стороны Франции, и Фултон вернулся в Соединенные Штаты.

Научно-исследовательские проекты были поручены Наполеоном новым университетам, политехническим институтам и Ecole polytechnique, которая предлагала систематическую подготовку в области инженерии. Такие крупные французские научные деятели, как Монж и Лаплас, преподавали там, проводя исследования.

Поскольку премии по тем временам были колоссальные, большое число ученых, ранее пренебрегавших электричеством, сейчас стали усиленно работать в этой области

Наполеоновское покровительство наукам часто подчинялось его военным целям. Во времена консульства Ecole polytechnique стала фактически военной академией, а в 1804 году она была полностью реорганизована по требованиям военных (несмотря на протесты Монжа и других ученых). В 1808 году был создан Университет Франции (или Императорский университет), который должен был контролировать все образование в стране. Образование во Франции было унифицировано, и во всех школах и университетах преподавали по единым программам, утвержденным лично императором.

Поддержка Наполеоном научных исследований и объемы ее финансирования намного опережали свое время, были уникальны на фоне отношения к науке в других странах и, безусловно, привели к выдающимся результатам для Франции. А принципы проведенной им организации науки и образования до сих пор остаются актуальными.

Видео:Теорема НаполеонаСкачать

Урок-лекция «Некоторые геометрические увлечения Наполеона»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Развитие управляющих функций мозга ребёнка: полезные советы и упражнения для педагогов

Сертификат и скидка на обучение каждому участнику

« Некоторые геометрические увлечения Наполеона»

Диамбекова Алла Лазаровна

педагог МКОУ ДОД ДДТ Дигорского района РСО-Алания.

Видео:Теоремы XX века!Скачать

Цель занятия – изучение некоторых геометрических увлечений Наполеона.

Видео:Теорема о трёх медианахСкачать

Задачи – а) рассмотреть три доказательства теоремы Наполеона;

Видео:Теорема о точке пересечения медиан треугольника. Доказательство. 8 класс.Скачать

б) ознакомиться с любимыми геометрическими головоломками императора;

Математика как основа всех наук во все времена привлекала пытливые неординарные умы. Юрист Пьер Ферма (1601-1665) известен как самый загадочный математик среди слуг «царицы наук». Священник Иван Первушин (1827-1900) справился с вычислением простого числа Мерсенна с показателем 61 и нашёл делители для чисел Ферма с индексом 12 и 23, что являлось в теории чисел того времени очень большим достижением. Император Франции Наполеон Бонапарт (1769-1821) не упускал возможности позаниматься геометрией. Этот список можно продолжить, но я хочу остановиться на Наполеоне I .

Из истории всем известно, что император Франции был блестящим полководцем и великим государственным деятелем. Книг о Наполеоне — более двухсот тысяч! Историки знают, во что одевался Наполеон, что было у него на ногах, сколько стоили его носовые платки, что он любил есть и во сколько завтракал, каким был распорядок его дня. Академик Фредерик Массон на рубеже XX века выпустил 13-томное исследование «Наполеон и его семья», посвященное практически всем сторонам жизни Наполеона. Но в них мало написано о математических способностях великого императора.[2]

Бонапарт-математик – это скрытая от многих страница истории. В декабре 1778 года Наполеон был принят в колледж в Отёне, главным образом с целью обучения французскому языку. Особых успехов Наполеон добился в математике. Благодаря победе в конкурсе «Ожерелье королевы», он был принят в Королевскую кадетскую школу в Париже. Обладая аналитическим умом, он добился определенных успехов в области математики. Своими знаниями он поражал многих великих математиков того времени. За заслуги в математике он был избран академиком Французской академии наук и стал магистром математики. [6]

У императора было увлечение – составление геометрических задач. Некоторые его задачи отличаются простотой постановки и допускают изящные решения.[1]

Он находил время заниматься геометрией для собственного удовольствия, чувствовал в ней красоту и объект, достойный приложения остроумия и изобретательности. Одно из свидетельств тому – несколько составленных им задач на построение, вычисление неизвестной величины, доказательство утверждений евклидовой геометрии, а также геометрические игры-головоломки.

На сторонах произвольного треугольника АВС внешним образом построены как на основаниях равносторонние треугольники (рис. 1). Доказать, что центры этих треугольников также являются вершинами равностороннего треугольника.

📸 Видео

Средняя линия. Теорема о средней линии треугольникаСкачать

ЕГЭ 2024. ВСЁ ПРО ТРЕУГОЛЬНИКИ за 15 минутСкачать

Теорема Наполеона и операции над векторамиСкачать

ТЕОРЕМА СИНУСОВ И ТЕОРЕМА КОСИНУСОВ. Тригонометрия | МатематикаСкачать

Теорема НаполеонаСкачать

Теорема о средней линии треугольника. Доказательство. 8 класс.Скачать

100. Теорема о площади треугольникаСкачать

Теорема о биссектрисе угла треугольника | Осторожно, спойлер! | Борис Трушин |Скачать

Шаталов за одну минуту доказывает теорему, на которую традиционно выделяется 45 минут урока!Скачать

Napoleon’s TheoremСкачать