О чем эта статья:
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).
- Основные понятия
- Формула радиуса окружности
- Если известна площадь круга
- Если известна длина
- Если известен диаметр окружности
- Если известна диагональ вписанного прямоугольника
- Если известна сторона описанного квадрата
- Если известны стороны и площадь вписанного треугольника
- Если известна площадь и полупериметр описанного треугольника
- Если известна площадь сектора и его центральный угол
- Если известна сторона вписанного правильного многоугольника
- Скачать онлайн таблицу
- Круг. Окружность (центр, радиус, диаметр)
- Отрезки и прямые, связанные с окружностью. Теорема о бабочке
- Отрезки и прямые, связанные с окружностью
- Свойства хорд и дуг окружности
- Теоремы о длинах хорд, касательных и секущих
- Доказательства теорем о длинах хорд, касательных и секущих
- Теорема о бабочке
- 🔥 Видео
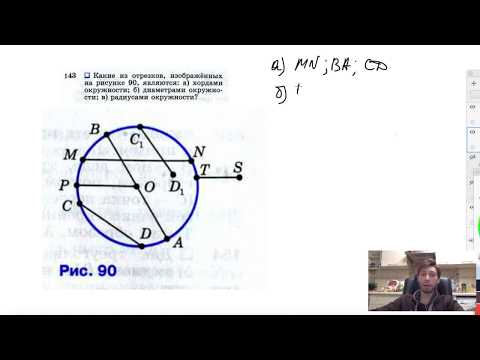
Видео:№143. Какие из отрезков, изображенных на рисунке 90, являются: а) хордами окружности; б) диаметрамиСкачать
Основные понятия
Прежде чем погружаться в последовательность расчетов, важно понять разницу между понятиями.
Окружность — замкнутая плоская кривая, все точки которой равноудалены от центра, которая лежит в той же плоскости. Если говорить проще, то это замкнутая линия, как, например, обруч и кольцо.
Круг — множество точек на плоскости, которые удалены от центра на расстоянии равном радиусу. Иначе говоря, плоская фигура, ограниченная окружностью, как мяч и блюдце.
Радиус — это отрезок, который соединяет центр окружности и любую точку на ней. Общепринятое обозначение радиуса — латинская буква R.
Возможно тебе интересно узнать — как найти длину окружности?
Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Формула радиуса окружности
Определить способ вычисления проще, отталкиваясь от исходных данных. Далее рассмотрим девять формул разной степени сложности.
Видео:Радиус и диаметрСкачать

Если известна площадь круга
R = √ S : π, где S — площадь круга, π — это константа, которая выражает отношение длины окружности к диаметру, она всегда равна 3,14.
Видео:Радиус описанной окружностиСкачать

Если известна длина
R = P : 2 * π, где P — длина (периметр круга).
Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курс подготовки к ЕГЭ по математике (профиль).
Видео:Длина окружности. Площадь круга - математика 6 классСкачать

Если известен диаметр окружности
R = D : 2, где D — диаметр.
Диаметр — отрезок, который соединяет две точки окружности и проходит через центр. Радиус всегда равен половине диаметра.
Видео:Математика 3 класс (Урок№33 - Круг. Окружность (центр, радиус, диаметр)Скачать

Если известна диагональ вписанного прямоугольника
R = d : 2, где d — диагональ.
Диагональ вписанного прямоугольник делит фигуру на два прямоугольных треугольника и является их гипотенузой — стороной, лежащей напротив прямого угла. Если диагональ неизвестна, теорема Пифагора поможет её вычислить:
d = √ a 2 + b 2 , где a, b — стороны вписанного прямоугольника.
Видео:Длина окружности. Математика 6 класс.Скачать

Если известна сторона описанного квадрата
R = a : 2, где a — сторона.
Сторона описанного квадрата равна диаметру окружности.
Видео:Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

Если известны стороны и площадь вписанного треугольника
R = (a * b * c) : (4 * S), где a, b, с — стороны, S — площадь треугольника.
Видео:Окружность. Как найти Радиус и ДиаметрСкачать

Если известна площадь и полупериметр описанного треугольника
R = S : p, где S — площадь треугольника, p — полупериметр треугольника.
Полупериметр треугольника — это сумма длин всех его сторон, деленная на два.
Видео:Длина окружности. Площадь круга. 6 класс.Скачать

Если известна площадь сектора и его центральный угол
R = √ (360° * S) : (π * α), где S — площадь сектора круга, α — центральный угол.
Площадь сектора круга — это часть S всей фигуры, ограниченной окружностью с радиусом.
Видео:РАДИУС ОКРУЖНОСТЬ ДИАМЕТР КРУГ / 3 КЛАСС МАТЕМАТИКА. ЧТО ТАКОЕ ОКРУЖНОСТЬ ? ЧТО ТАКОЕ РАДИУС ?Скачать

Если известна сторона вписанного правильного многоугольника
R = a : (2 * sin (180 : N)), где a — сторона правильного многоугольника, N — количество сторон.
В правильном многоугольнике все стороны равны.
Видео:№641. Отрезки АВ и АС являются отрезками касательных к окружности с центром О, проведенными изСкачать

Скачать онлайн таблицу
У каждой геометрической фигуры много формул — запомнить все сразу бывает действительно сложно. В этом деле поможет регулярное решение задач и частый просмотр формул. Можно распечатать эту таблицу и использовать, как закладку в тетрадке или учебнике, и обращаться к ней по необходимости.
Видео:Окружность и круг, 6 классСкачать

Круг. Окружность (центр, радиус, диаметр)
Этот видеоурок доступен по абонементу
У вас уже есть абонемент? Войти
Данный урок посвящён изучению окружности и круга. Также учитель научит отличать замкнутые и незамкнутые линии. Вы познакомитесь с основными свойствами окружности: центром, радиусом и диаметром. Выучите их определения. Научитесь определять радиус, если известен диаметр, и наоборот.
Видео:Геометрия 8 класс (Урок№28 - Свойства хорд окружности.)Скачать

Отрезки и прямые, связанные с окружностью. Теорема о бабочке
 Отрезки и прямые, связанные с окружностью Отрезки и прямые, связанные с окружностью |
 Свойства хорд и дуг окружности Свойства хорд и дуг окружности |
 Теоремы о длинах хорд, касательных и секущих Теоремы о длинах хорд, касательных и секущих |
 Доказательства теорем о длинах хорд, касательных и секущих Доказательства теорем о длинах хорд, касательных и секущих |
 Теорема о бабочке Теорема о бабочке |
Видео:Окружность. 7 класс.Скачать

Отрезки и прямые, связанные с окружностью
| Фигура | Рисунок | Определение и свойства | ||||||||||||||||||||||||||
| Окружность |  | |||||||||||||||||||||||||||
| Круг |  | |||||||||||||||||||||||||||
| Радиус |  | |||||||||||||||||||||||||||
| Хорда |  | |||||||||||||||||||||||||||
| Диаметр |  | |||||||||||||||||||||||||||
| Касательная |  | |||||||||||||||||||||||||||
| Секущая |  | |||||||||||||||||||||||||||
| Окружность |
 |
Множество точек плоскости, находящихся на одном и том же расстоянии от одной точки — центра окружности

Конечная часть плоскости, ограниченная окружностью

Отрезок, соединяющий центр окружности с любой точкой окружности

Отрезок, соединяющий две любые точки окружности

Хорда, проходящая через центр окружности.
Диаметр является самой длинной хордой окружности

Прямая, имеющая с окружностью только одну общую точку.
Касательная перпендикулярна к радиусу окружности, проведённому в точку касания

Прямая, пересекающая окружность в двух точках
Видео:9 класс, 6 урок, Уравнение окружностиСкачать

Свойства хорд и дуг окружности
| Фигура | Рисунок | Свойство |
| Диаметр, перпендикулярный к хорде |  | Диаметр, перпендикулярный к хорде, делит эту хорду и стягиваемые ею две дуги пополам. |
| Диаметр, проходящий через середину хорды | Диаметр, проходящий через середину хорды, перпендикулярен к этой хорде и делит стягиваемые ею две дуги пополам. | |
| Равные хорды |  | Если хорды равны, то они находятся на одном и том же расстоянии от центра окружности. |
| Хорды, равноудалённые от центра окружности | Если хорды равноудалены (находятся на одном и том же расстоянии) от центра окружности, то они равны. | |
| Две хорды разной длины |  | Большая из двух хорд расположена ближе к центру окружности. |
| Равные дуги |  | У равных дуг равны и хорды. |
| Параллельные хорды |  | Дуги, заключённые между параллельными хордами, равны. |
| Диаметр, перпендикулярный к хорде |
 |
Диаметр, перпендикулярный к хорде, делит эту хорду и стягиваемые ею две дуги пополам.

Диаметр, проходящий через середину хорды, перпендикулярен к этой хорде и делит стягиваемые ею две дуги пополам.

Если хорды равны, то они находятся на одном и том же расстоянии от центра окружности.

Если хорды равноудалены (находятся на одном и том же расстоянии) от центра окружности, то они равны.

Большая из двух хорд расположена ближе к центру окружности.

У равных дуг равны и хорды.

Дуги, заключённые между параллельными хордами, равны.
Видео:Окружность, диаметр, хорда геометрия 7 классСкачать

Теоремы о длинах хорд, касательных и секущих
| Фигура | Рисунок | Теорема | ||||||||||||||||
| Пересекающиеся хорды |  | |||||||||||||||||
| Касательные, проведённые к окружности из одной точки |  | |||||||||||||||||
| Касательная и секущая, проведённые к окружности из одной точки |  | |||||||||||||||||
| Секущие, проведённые из одной точки вне круга |  | |||||||||||||||||
| Пересекающиеся хорды | ||
 | ||
| Касательные, проведённые к окружности из одной точки | ||
 | ||
| Касательная и секущая, проведённые к окружности из одной точки | ||
 | ||
| Секущие, проведённые из одной точки вне круга | ||
 | ||
| Пересекающиеся хорды |
 |
Произведения длин отрезков, на которые разбита каждая из хорд, равны:
Если к окружности из одной точки проведены две касательных, то длины отрезков касательных от этой точки до точек касания с окружностью равны.
Видео:Радиус Хорда ДиаметрСкачать

Доказательства теорем о длинах хорд, касательных и секущих
Теорема 1 . Предположим, что хорды окружности AB и CD пересекаются в точке E (рис.1).
Тогда справедливо равенство
Доказательство . Заметим, что углы BCD и BAD равны как вписанные углы, опирающиеся на одну и ту же дугу. Углы BEC и AED равны как вертикальные. Поэтому треугольники BEC и AED подобны. Следовательно, справедливо равенство
откуда и вытекает требуемое утверждение.
Теорема 2 . Предположим, что из точки A , лежащей вне круга, к окружности проведены касательная AB и секущая AD (рис.2).
Точка B – точка касания с окружностью, точка C – вторая точка пересечения прямой AD с окружностью. Тогда справедливо равенство
Доказательство . Заметим, что угол ABC образован касательной AB и хордой BC , проходящей через точку касания B . Поэтому величина угла ABC равна половине угловой величины дуги BC . Поскольку угол BDC является вписанным углом, то величина угла BDC также равна половине угловой величины дуги BC . Следовательно, треугольники ABC и ABD подобны (угол A является общим, углы ABC и BDA равны). Поэтому справедливо равенство
откуда и вытекает требуемое утверждение.
Теорема 3 . Предположим, что из точки A , лежащей вне круга, к окружности проведены секущие AD и AF (рис.3).
Точки C и E – вторые точки пересечения секущих с окружностью. Тогда справедливо равенство
Доказательство . Проведём из точки A касательную AB к окружности (рис. 4).
Точка B – точка касания. В силу теоремы 2 справедливы равенства
откуда и вытекает требуемое утверждение.
Видео:Вписанные и описанные окружности. Вебинар | МатематикаСкачать

Теорема о бабочке
Теорема о бабочке . Через середину G хорды EF некоторой окружности проведены две произвольные хорды AB и CD этой окружности. Точки K и L – точки пересечения хорд AC и BD с хордой EF соответственно (рис.5). Тогда отрезки GK и GL равны.
Доказательство . Существует много доказательств этой теоремы. Изложим доказательство, основанное на теореме синусов, которое, на наш взгляд, является наиболее наглядным. Для этого заметим сначала, что вписанные углы A и D равны, поскольку опираются на одну и ту же дугу. По той же причине равны и вписанные углы C и B . Теперь введём следующие обозначения:
Воспользовавшись теоремой синусов, применённой к треугольнику CKG , получим
Воспользовавшись теоремой синусов, применённой к треугольнику AKG , получим
Воспользовавшись теоремой 1, получим
Воспользовавшись равенствами (1) и (2), получим
Проводя совершенно аналогичные рассуждения для треугольников BGL и DGL , получим равенство
откуда вытекает равенство
что и завершает доказательство теоремы о бабочке.
🔥 Видео
Уравнение окружности (1)Скачать


































