Вычислить используя основную теорему о вычетах где l окружность

Определение. Точки комплексной плоскости, в которых однозначная функция f(z) является аналитической, называют правильными точками этой функции, а точки, в которых f(z) не является аналитиче­ской, называют особыми точками (в частности, точки, в которых f(z) не определена).

Определение. Точка z₀ называется нулем (корнем) порядка (кратности) аналитической функции f(z),если:

б) существует, конечен и не равен нулю.

Если целые положительные числа), то­гда – нули (корни) этого многочлена, которые имеют соответственно порядки (кратности) .

Определение. Пусть f(z) аналитическая функция в окрестности точки z₀, за ис­ключением самой точки z₀. В этом случае точка z₀ называется изолированной особой точкой функции f(z).

Различают изолированные особые точки одно­значной функции трёх типов:

1) устранимую особую точку – изолированную особую точку z₀ , в которой существует конечный предел:

2) полюс k-го порядка – изолированную особую точку z₀, в которой существует конечный предел, не равный нулю:

если , то z₀ – полюс первого порядка (простой полюс);

3) сущест­венно особую точку – изолированную особую точку z₀, которая не является ни уст­ранимой, ни полюсом. То есть не существует, ни конечный, ни бесконечный.

Теорема (о связи между нулем и полюсом). Если точка z₀ – нуль порядка к функции f(z), то для функции 1/f(z) эта точка является полюсом порядка к.

Пусть f(z) – функция, аналитическая в каждой точке об­ласти D, за исключением конечного числа изолированных осо­бых точек, и L — кусочно-гладкий замкнутый контур, целиком лежащий в области D и не проходящий через особые точки функции f(z).

Если в области, ограниченной контуром L, не содержится особых точек функции f(z), то по основной теореме Коши

Если же в области, ограниченной контуром L, имеются особые точки функции f(z), то значение этого интеграла, вообще говоря, отлично от нуля.

Определение. Вычетом аналитической функции f(z) относительно изо­лированной особой точки z₀ (или в точке z₀) называется комплексное число, равное значению интеграла , где L – любой кусочно-гладкий замкнутый контур, лежащий в облас­ти аналитичности функции f(z) и содержащий внутри себя един­ственную особую точку z₀ функции f(z).

Вычет f(z) относительно точки z₀ обозначается симво­лом resf(z₀)(Resf(z₀)) или так, что имеем:

Вычет функции относительно устранимой особой точки равен нулю:

Вычет f(z) относительно простого полюса можно найти по формуле:

Вычет f(z) относительно полюса порядка к находят по формуле:

Если причем точка является простым нулем и не является нулем для , то:

Основная теорема Коши о вычетах. Если функция f(z) аналитическая в замкнутой области , ограниченной контуром L, за исключением конечного числа особых точек , лежащих внутри ,то:

Эта теорема имеет большое значение для приложений.

Од­но из них – это вычисление некоторых интегралов от функции комплексной переменной.

Замечание. В предыдущих рассуждениях о вычетах неявно предпола­галось, что рассматриваются конечные изолированные особые точки (это ясно из того, что интеграл по замкнутому контуру по умолчанию брался в положительном направлении, т.е. против часовой стрелки, а особая точка при этом попадает внутрь конту­ра только в случае, когда она конечна). В случае же, когда рас­сматривается бесконечно удаленная точка, ситуация несколько иная. Точнее, сформулируем это так.

Определение. Вычетом функции f(z) относительно бесконечно уда­ленной точки называют интеграл:

где L – замкнутый кусочно-гладкий контур, целиком лежащий в той ок­рестности точки , в которой функция f(z) является анали­тической. Интегрирование по Lсовершается в отрицательном направлении этого контура, т.е. так, чтобы при обходе контура бесконечно удаленная точка оставалась слева. Таким образом:

Найти интеграл от функции комплексного переменного, используя основную теорему Коши о вычетах:

Решение

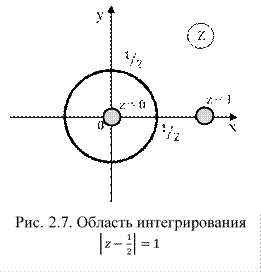
1) Определим изолированные особые точки подинтегральной функции, согласно теореме (2.47):

2) Определим точки, лежащие внутри области интегрирования, изобразим область графически (рис. 2.7).

Точку z = 1 не рассматриваем, так как она не лежит внутри области .

3) Определим тип рассматриваемой изолированной особой точки z = 0. Найдем предел по формуле (2.41):

Так как предел существует, то z = 0 – полюс первого порядка (простой полюс).

4) Найдем вычет функции относительно простого полюса z = 0, используя формулу (2.44):

5) Определим значение интеграла по основной теореме Коши о вычетах (2.47):

Найти интеграл от функции комплексного переменного, используя основную теорему Коши о вычетах:

Решение

1) Определим изолированные особые точки подинтегральной функции, согласно теореме (2.47):

2) Определим точки, лежащие внутри области интегрирования, изобразим область (рис. 2.8).

Обе особые точки лежат внутри области интегрирования.

3) Определим тип рассматриваемых изолированных особых точек . Найдем предел по формуле (2.41):

так как предел существует, то z = -1 – полюс первого порядка (простой полюс).

так как предел существует, то z = -2 – полюс первого порядка (простой полюс).

4) Найдем вычеты функции относительно простых полюсов и используя формулу (2.44):

5) Определим значение интеграла по основной теореме Коши о вычетах (2.47)

Срочно?
Закажи у профессионала, через форму заявки
8 (800) 100-77-13 с 7.00 до 22.00

Видео:ТФКП. Вычеты в особых точках. Вычеты в полюсах. Примеры вычисления вычетов.Скачать

Вычисление интегралов с помощью вычетов

1. Вычисление интегралов по замкнутому контуру. Пусть функция f(z) имеет внутри замкнутого контура Г только изолированные особые точки. Тогда интеграл от f(z) по контуру Г можно найти, применяя теорему 27.1 о вычетах: вычисляя вычеты в особых точках, находящихся внутри контура Г, складывая эти вычеты и умножая сумму на 2тгг, мы и получим искомый интеграл.

Г1 р и м е р 28.1. Вычислить интеграл

Р е ш е н и е. Внутри окружности z = 2 находятся две особые точки функции f(z) = ( ₂2 ₊i)(^+ 3) 2 ’ а именно z i = U z 2 = —Ц третья особая точка z% = — 3 лежит вне этой окружности. Вычеты в точках ±г были найдены в примере 27.5: res*/ = 0,01(7-N), res_*/ = 0,01(7— г). Применяя формулу (27.2), имеем:

Если функция f(z) имеет в расширенной комплексной плоскости С только изолированные особые точки, то вместо вычисления суммы вычетов в конечных особых точках бывает проще найти вычет в бесконечно удаленной точке и воспользоваться теоремой 27.10 о сумме вычетов.

Пример 28.2. Вычислить интеграл

Решение. Функция f(z) = имеет восемь особых точек

— решений уравнения z s 4- 1 = 0. Каждая из этих точек Zk является полюсом второго порядка, поскольку в окрестности точки Zk функция f(z) имеет вид f(z) = , где h(z) аналитична в окрестности

точки Zk и h(zk) ф 0. Все особые точки лежат внутри окружности z = 2. Вычисление вычетов во всех этих точках весьма трудоемко. По к данной функции применима теорема 27.10, которая дает

Поэтому достаточно найти вычег в точке zq = эо. Воспользуемся формулой (27.13). Здесь

Функция g(w) представима в виде — 1 ^ ^. где h(w) = ——

Поскольку hi(w) аналитична в окрестности точки wq = 0 и h(0) Ф 0, то вычет reso$ легко найти по формуле (27.6 / ): reso# = h(0) = 1. Из (27.2), (28.1) и (27.13) получаем:

(см. формулы (12.2)). При изменении р от 0 до 2тг точка г описывает окружность z = 1. Поэтому после перехода к переменному 2 мы получим интеграл по единичной окружности от функции, представимой в виде отношения двух многочленов; такие функции называются рациональными дробями или дробно-рациональными функциями.

Пример 28.3. Вычислить интеграл

Решен и е. Выполняя указанные выше подстановки, получим, что данный интеграл равен

Разложим знаменатель на множители, для чего найдем корни уравнения az 2 — (а 2 + )z + а = 0. Дискриминант

Следовательно, подынтегральная функция f(z) имеет две особые точки z — а и 22 = 1/а, каждая из которых является полюсом первого порядка. Так как по условию |а| оо. Пользуясь соотношениями (28.2) и (28.3), получим нужное равенство:

где сумма берется по всем особым точкам из верхней полуплоскости.

Бели полуокружность 7(Я) лежит в нижней полуплоскости, то соответствующий контур Г“ будет обходиться по часовой стрелке (такое направление возникает оттого, что отрезок [—Я, Я] в любом случае должен проходиться слева направо, т.е. в направлении возрастания х). Поэтому в правой части (28.4) добавится знак минус. Теорема 28.4 доказана.

Пример 28.5. Вычислить интеграл

Решение. В данном случае f(z) = ^ ₊ уу • Проверим справедливость условия (28.3):

где h(z) = —-§—ту. Так как lim h(z) = 1, то при достаточно боль-

ших значениях z будет h(z) оо. получим (28.3). Проведепные оценки справедливы как для верхней, так и для нижней полуокружности. Поэтому в качестве 7(Л) можно выбрать любую из них. Пусть у(R) — верхняя полуокружность. Так как

то f(z) имеет две особые точки z — 3г, zo = —Зг, являющиеся полюсами второго порядка. Из них в верхней полуплоскости находится только z = Зг. Вычет в этой точке найдем по формуле (27.7) с тг = 2:

Заметим, что вычислить данный интеграл можно было и не прибегая к методам комплексного анализа, а находя первообразную подынтегральной функции. Но приведенное вычисление значительно проще.

Рассуждение, проведенное нами в примере 28.5 для проверки условия (28.3), без изменения подходит к любой функции f(z), представимой в виде отношения двух многочленов (т.е. рациональной дроби), если степень многочлена в знаменателе на две и более единицы превосходит степень многочлена в числителе. (В примере 28.5 степень многочлена в числителе равна 2, а в знаменателе — 4.) Следующая теорема показывает, что условию (28.3) удовлетворяет и другой важный класс функций, интегралы от которых возникают, например, в операционном исчислении (см. гл. VIII).

Теорема 28.6 (лемма Жордана). Пусть функция F(z) аполитична в полуплоскости lm z ^ —а, за исключением конечного числа изолированных особых точек, и lim F(z) = 0. Если 7(R) — дуга

окружности z = 7?, расположенная в полуплоскости Ini 2 ^ —а, то

Доказательство. Рассмотрим вначале случай а > 0. Обозначим через М(7?) максимум модуля F(z) на дуге 7(7?). Поскольку lira F(z) = 0, то

Разобьем 7(7?) на три части 7i (Л), 72(7?) и 7з(Т?) (рис. 50): дуги 7i(R) и 72(Я) заключены между прямой у = —а и осью ОА», а 7з(Т?) является полуокружностью, лежащей в полуплоскости Im z ^ 0. Очевидно, что интеграл по 7(7?) равен сумме интегралов по этим трем дугам. Оценим каждый из них в отдельности.

В точках z = х + iy дуг 71 (7?) и 72(7?) будет —у и 72(7?) (в радианах). Легко видеть (см. рис. 50), что siny? =

откуда ?>(7?) = arcsin —. Поэтому /(7?) = R

Таким образом, в случае а > 0 теорема доказана. Если а ^ 0, то дуга ‘y(R) лежит в полуплоскости Im z ^ 0 и является частью дуги 73(R); части 7i (R) и 7г(Я) в этом случае отсутствуют. Для 7(R) справедливы рассуждения, проведенные выше для 73(7?), и теорема 28.G полностью доказана.

Смысл теоремы 28.6 состоит в том. что функция F(z) может стремиться к нулю сколь угодно медленно (заметим, что в примере 28.5 убывание функции f(z) при z —? оо было достаточно быстрым как |z|“ 2 ). Но умножение на e ltz обеспечивает стремление интеграла по 7(R) к нулю.

Замечание. Для случая t 0. В случае t — 0 теорема 28.6 неверна.

П р и м е р 28.7. Вычислить интегралы

Таким образом, действительная и мнимая части функции f(x) и являются теми функциями, интегралы от которых нужно найти. Поэтому

ются теми функциями, интегралы от которых нужно найти. Поэтому

• ——- dx и возьмем от него действиям + 9
• — 00

тельную и мнимую части, то получим искомые величины.

Функция F(z) = .Д удовлетворяет условиям теоремы 28.6: она z «f 9

имеет только две особые точки z •> = ±3t и lim —- = 0. Ес-

ли 7(/?) дуга окружности z = R, расположенная в полуплоскости Im z > 0. то согласно tcodcmc 28.6

(мы взяли в (28.5) t = 2). Значит, можно применить теорему 28.4,

согласно которой интеграл / ——- dx равен сумме вычетов функ-

ции f(z) = ——- в особых точках из верхней полуплоскости 1т z > z I J

О, умноженной на 2т. В полуплоскости Im z > 0 лежит единственная

особая точка Z = Зг функции f(z). Так как f(z) = —-———,

то z = Зг — полюс первого порядка. Вычет в этой точке можно найти по любой из сЬоомул (27.,’В. (27.6L (27.63. Ппименим (27.63. Злесь

Действительная и мнимая части полученного числа и будут искомыми и I ггегралам и:

(Заметим, что равенство нулю первого из этих интегралов непосредственно следует из того, что он является интегралом от нечетной функции по интервалу, симметричному относительно начала координат.)

Видео:ТФКП. Вычисление интегралов с помощью вычетовСкачать

VMath

Инструменты сайта

Основное

Навигация

Информация

Действия

Содержание

Видео:ТФКП. Вычисление интегралов с помощью вычетов. Теорема Коши о вычетах. Примеры решенийСкачать

Глава 6. Вычеты функций и их применение

Видео:Вычисление интегралов с помощью вычетовСкачать

Вычет функции относительно изолированной особой точки. Основная теорема о вычетах

Вычетом функции $f(z)$ относительно изолированной особой точки $z_0$ называется коэффициент $c_$ при $(z-z_0)^$ в разложении в ряд Лорана функции $f(z)$ в окрестности $z_0$. $$ mboxf(z_0) = c_. $$

Вычетом функции $f(z)$ относительно изолированной особой точки $z_0$ называется интеграл $$ mboxf(z_0) =frac1ointlimits_L f(z),dz, $$ где $L$ — произвольный контур в кольце $0 r$, которое иногда называют окрестностью бесконечно удаленной точки, $$ f(z)=sumlimits_^infty c_kz^k=F_1(z)+F_2(z) =sumlimits_^infty c_kz^k +sumlimits_^inftyfrac<c_>. $$ В этом случае $F_1(z)$ называют главной частью, а $F_2(z)$ — правильной частью.

В зависимости от поведения функции $f(z)$ в окрестности $z=infty$ введена следующая классификация:

— Особенность в точке $z=infty$ устранимая, если все $c_k=0$, $k=1,2,ldots$, т.е. если $f(z)=F_2(z)$ для $|z|>r$. В этом случае $$ limlimits_f(z)=c_0. $$ Очевидно, что $$ frac1ointlimits_f(z),dz=-c_, $$ где $L^-$ — произвольный контур, ориентированный по часовой стрелке, содержащий внутри себя окружность $|z|=r$.

Можно считать, что точка $z=infty$ находится внутри контура $L^-$. Если двигаться по контуру $L^-$ по часовой стрелке, то точка $z=infty$ остается слева.

Видим, что в случае, когда $z=infty$ — устранимая особая точка, то вычет не обязательно равен нулю!

— Точка $z=infty$ есть полюс порядка $m$, если $f(z)=sumlimits_^m c_k z^k+F_2(z)$ и $c_mne0$. В этом случае, очевидно, $$ limlimits_f(z)=infty. $$

$$ ointlimits_f(z),dz=sumlimits_^infty c_ ointlimits_frac+sumlimits_^m c_k ointlimits_z^k,dz= $$ $$ =-c_intlimits_Lfracz=-2pimathbf i c_, $$ потому, что $displaystyleointlimits_z^k,dz=-ointlimits_L z^k,dz=0$, когда $kne-1$;

— Точка $z=infty$ является существенно особой точкой, если $f(z)=sumlimits_^infty c_kz^k+F_2(z)$ и имеется бесконечное число чисел $c_k$, не равных нулю. В данном случае функция из-за первого слагаемого не имеет предела при $ztoinfty$. $$ ointlimits_f(z),dz=sumlimits_^infty c_k ointlimits_z^k,dz=-2pi mathbf i c_. $$

Вычетом функции $f(z)$ в бесконечно удаленной точке называется $$ mboxf(infty)=frac1ointlimits_f(z),dz, $$ где $L^-$ — произвольный замкнутый контур, ориентированный по часовой стрелке, принадлежащий множеству $|z|>r$ (где функция $f(z)$ аналитична).

Кроме того, если $f(z)=sumlimits_^infty c_kz^k$ — ряд Лорана функции во внешности окружности $|z|=r$, то $$ mboxf(infty)=-c_. $$

Теорема о сумме вычетов Пусть функция $f(z)$ аналитична на всей плоскости $z$ за исключением конечного числа изолированных особых точек $z_1,z_2,dots,z_N$. Тогда сумма всех вычетов этой функции, включая вычет в бесконечно удаленной точке, равна нулю: $$ sumlimits_^Nmboxf(z_k)+mboxf(infty)=0. $$

Р е ш е н и е.
Все особые точки $z_k=sqrt[4]$, $sqrt[3]$ лежат в круге $|z|=2$. Вычисление вычетов в этих точках довольно затруднительно, поэтому воспользуемся формулой $$ I=2pi isumlimits_^infty mboxf(z_k)=-2pi imboxf(infty). $$ Представим функцию в виде $$ frac<z^><4z^6left(1+cfrac1right)^2z^ left(1-cfrac1right)^3>= $$ $$ =frac4left(1-frac1+frac1-dotsright)^2 left(1+frac1+frac1right)^3=frac4-frac1 +dots . $$

Тогда $mboxf(infty)=dfrac14$ и интеграл равен $-2pi imboxf(infty)=-dfrac2$.

О т в е т: $-dfrac2$.

Видео:ТФКП. Интегральная формула Коши. Примеры решений типовых задач. Решение контурных интегралов.Скачать

Вычисление определенных интегралов с помощью вычетов

Некоторые определенные интегралы от функций вещественного переменного удается преобразовать в интеграл по замкнутому контуру от функции комплексного переменного, что позволяет применить для вычисления этих интегралов основную теорему о вычетах. Часто удается достаточно просто получить ответ и в тех случаях, когда применение других методов анализа оказывается затруднительным.

I. Интеграл вида $I=intlimits_0^R(cos,sin),dx,$

где $R(u,v)$ — рациональная функция двух переменных.

Подстановка $z=e^$ даст для $$ begin costheta=dfrac12left(e^+e^right) =dfrac12left(z+dfrac1zright), \ sintheta=dfrac1left(e^-e^right) =dfrac2left(z-dfrac1zright), \ dtheta=dfrac end $$ и превратит вещественный интеграл в комплексный. При изменении $theta$ от $0$ до $2pi$ комплексная переменная пробегает замкнутый контур — окружность $|z|=1$ в положительном направлении. Окончательно интеграл примет вид $$ I=frac1iointlimits_Fleft(z+frac1z,z-frac1zright) frac,. $$

Пример. Вычислить интеграл $$ intlimits_0^frac,quad a>1. $$

Р е ш е н и е.
Положим $e^=z$. При изменении $x$ от 0 до $2pi$ переменная $z$ пробегает окружность $|z|=1$ в положительном направлении. Выразим $$ cos x=frac12left(e^+e^right)=frac, $$ и $$ dz=ie^dx=izdx,quadhboxquad dx=frac. $$ Тогда $$ I=ointlimits_frac<izleft(cfrac+aright)> =frac2iointlimits_frac. $$

Корни знаменателя $z_1=-a+sqrt$, $z_2=-a-sqrt$ — простые полюсы, $|z_1| 0$.

Вычислить интеграл $ I=intlimits_^inftyfrac.$

Р е ш е н и е.
Аналитическое продолжение подынтегральной функции в верхнюю полуплоскость, а именно функция $$ f(z)=frac1, $$ удовлетворяет всем условиям, относящимся к вычислению интегралов с помощью вычетов. Особыми точками функции в верхней полуплоскости являются точки $$ z_k=e^<tfrac4(2k+1)>,quad k=0,1, $$ причем обе эти точки — полюсы 1-го порядка. Поэтому $$ I=2pi isumlimits_^1 mboxf(z_k)=frac2. $$

III. Несобственные интегралы вида $I=intlimits_^infty R(x)cos,dx, ,, I=intlimits_^infty R(x)sin,dx$,

где $R(x)=P_m(x)/Q_n(x)$ — правильная рациональная дробь, не имеющая особых точек на действительной оси. Тогда begin intlimits_^infty R(x)cos,dx = mboxleft( 2pi mathbf i sumlimits_ mboxR(z_k)e^right), end begin intlimits_^infty R(x)sin,dx = mboxleft( 2pi mathbf i sumlimits_ mboxR(z_k)e^right), end где вычеты берутся во всех полюсах $z_k$ функции $R(z)$, расположенных в верхней полуплоскости $mboxz>0$.

Интегралы вычисляются с помощью леммы Жордана:

Лемма Жордана

Пусть функция $f(z)$ аналитична в полуплоскости $mboxz>0$, за исключением конечного числа изолированных особых точек, и пусть $M(R)$ есть максимум модуля $f(z)$ на полуокружности $gamma_=<zin mathbb C_: |z|=R, mbox z >0 >$.
Если $M(R)to0$ при $Rtoinfty$, то для любого действительного числа $lambda>0$, то $$ intlimits_f(z)e^,dzto0quadhboxquad Rtoinfty, $$

Для $lambda 0, alpha>0$.

Р е ш е н и е.
Чтобы иметь возможность воспользоваться леммой Жордана, заметим, что в силу формулы Эйлера $$ I=mboxI_1 =mboxintlimits_^infty frac<e^> ,dx. $$

Аналитическое продолжение подынтегральной функции интеграла $I_1$ — функция $dfrac<e^>$ имеет в верхней полуплоскости единственную особую точку $z_1=ia$, являющуюся простым полюсом. Поэтому по основной теореме о вычетах $$ I_1=2pi mathbf i mboxleft(frac<e^>Big|_ right)=fracpie^quadhboxquad I=fracpie^. $$

Видео:ТФКП. Вычисление несобственных интегралов от рациональных функций. Вычислить интеграл по вычетам.Скачать

Логарифмический вычет. Принцип аргумента

Логарифмической производной функции $f(z)$ называется производная ее логарифма $left(ln right)’= frac$.

Пусть $z_0$ — нуль порядка $n$, $z_1$ — полюс порядка $p$. Запишем разложения в ряд Лорана логарифмической производной в окрестности нуля и полюса функции $f(z)$. $$ left(ln right)’= frac+b_1+b_2(z-z_0)+dots quad Rightarrow $$ $n$-кратный нуль функции $f(z)$ является для логарифмической производной простым полюсом, причем вычет логарифмической производной в этой точке равен кратности нуля, то есть $n$. $$ left(ln right)’= frac+c_1+c_2(z-z_1)+dots quad Rightarrow $$ $p$-кратный полюс функции $f(z)$ является для логарифмической производной простым полюсом, причем вычет логарифмической производной в этой точке равен порядку полюса, взятому с обратным знаком, то есть $-p$.

Логарифмическим вычетом функции $f(z)$ в точке $z=a$ называется вычет ее логарифмической производной $ frac$ в этой точке, т.е. значение $$ mboxfrac=fracointlimits_ fracdz, $$ где в качестве контура $L$ интегрирования можно взять любую окружность с центром в точке $z=a$, целиком лежащую в указанной проколотой окрестности этой точки.

Если $f(z)$ является аналитической функцией на замкнутом контуре $L$ и не имеет нулей на этом контуре, то значение $$ mbox frac=fracointlimits_ fracdz $$ называют логарифмическим вычетом функции $f(z)$ относительно контура $L$.

Теорема о логарифмическом вычете

Пусть непостоянная функция $f(z)$ аналитична всюду в односвязной области $D$ и на ее границе — кусочно-гладком контуре $L$, кроме, возможно, некоторого конечного числа полюсов. Пусть также функция имеет конечное число нулей, причем на контуре $L$ нет ни нулей, ни полюсов функции. Тогда $$ mbox frac=N-P, $$ где $N$ и $P$ — общее количество нулей и полюсов функции $f(z)$ в $D$, причем каждый нуль следует считать сколько раз, какова его кратность, а каждый полюс — каков его порядок.

Логарифмический вычет многочлена $P_n(z)$ степени $n$ относительно контура $L$, на котором нет нулей $P_n(z)$, равен числу нулей многочлена (с учетом их кратности) внутри контура.

Пусть непостоянная функция $f(z)$ аналитична всюду в односвязной области $D$ и на ее границе — кусочно-гладком контуре $L$, кроме, возможно, некоторого конечного числа полюсов. Пусть также функция имеет конечное число нулей, причем на контуре $L$ нет ни нулей, ни полюсов функции. Тогда приращение аргумента функции $f(z)$ при обходе в положительном направлении контура $L$ равно произведению $2pi$ на разность числа нулей и полюсов функции $f(z)$, расположенных в области $D$, причем каждый нуль следует считать сколько раз, какова его кратность, а каждый полюс — каков его порядок. $$ Delta_Larg f(z)=2pi(N-P), $$ $$ N=q_1+q_2+ldots+q_m, quad P=p_1+p_2+ldots+p_k, $$ $q_i$ — кратность нуля $a_i$, $i=1,ldots,m$, $p_j$ — кратность полюса $b_j$, $j=1,ldots,k$.

Видео:Теорема Коши о вычетахСкачать

Теорема Руше

Пусть функции $f(z)$ и $varphi(z)$ являются аналитическими в замкнутой области $D$, причем на границе $C$ этой области имеет место неравенство: $|f(z)|_>|varphi(z)|_$. Тогда полное число нулей (с учетом их кратности) в $D$ функции $F(z)=f(z)+varphi(z)$ равно полному числу нулей (с учетом их кратности) функции $f(z)$.

Найти число нулей функции $F(z)=z^8-4z^5+z^2-1$ в единичном круге.

Пусть $f(z)=-4z^5$, $varphi(z)=z^8+z^2-1$. Граница $C$ заданной области — единичный круг $|z|=1$.

Выполнены все условия теоремы Руше. Функция $f(z)$ имеет корень $z=0$ кратности $5$, лежащий в $|z| |varphi(z)|. $$ Выполнены все условия теоремы Руше. Функция $f(z)$ в области $|z| tfkp/chapter6.txt · Последние изменения: 2021/05/04 15:25 — nvr

🌟 Видео

ТФКП. Теорема Коши о вычетах . Нули функции. Особые точки. Вычеты. Решение контурного интеграла.Скачать

Вычисление несобственных интегралов при помощи вычетовСкачать

Вычислить интеграл по заданному контуру. Интегрирование по части окружности и по отрезку прямой.Скачать

ТФКП. Вычислить интеграл от функции комплексного переменного по данной кривой. Дуга окружности.Скачать

ТФКП. Вычислить интеграл по замкнутому контуру. Теорема Коши о вычетах. Характер особой точки.Скачать

ТФКП. Вычислить интеграл. ЧУДЕСЕНКО. Контурный интеграл. Основная теорема Коши о вычетах.Скачать

Вычеты в особых точках ФКП , Порядок вычетаСкачать

ТФКП. Вычисление контурного интеграла по вычетам.Скачать

Попов В.Ю. - ТФКП. Лекции - 12. ВычетыСкачать

Интегральная формула Коши - примерыСкачать

ТФКП. Вычислить интеграл по замкнутому контуру с помощью вычетов. Пример из ДемидовичаСкачать