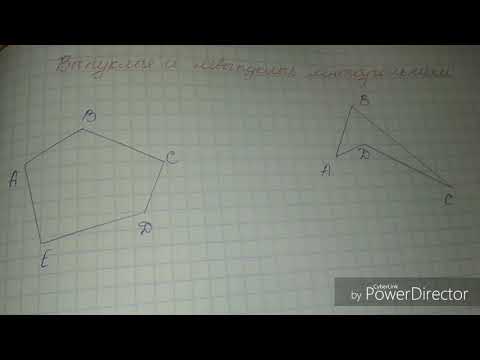
Нарисуйте выпуклые и невыпуклые четырехугольники пятиугольники

Видео:Сумма внутренних углов многоугольника. Выпуклые и невыпуклые многоугольники. 8 класс.Скачать

Ваш ответ

Видео:Выпуклые и невыпуклые многоугольникиСкачать

Похожие вопросы

• Все категории
• экономические 43,277
• гуманитарные 33,618
• юридические 17,900
• школьный раздел 606,658
• разное 16,822

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.

Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.

Видео:8 класс, 2 урок, Выпуклый многоугольникСкачать

Нарисуйте выпуклые и невыпуклые четырехугольники пятиугольники

Всякая простая замкнутая ломаная разбивает плоскость на две области — внутреннюю и внешнюю. На рисунке 16.1 внутренние обла­сти закрашены.

Фигура, образованная простой замкнутой ломаной и ограни­ченной ею внутренней областью, называется многоугольникам. Вер­шины ломаной сторонами, — углами многоугольник а. Точки многоугольника, не при­надлежащие его сторонам, называются внутренними.

Периметром многоугольника называется сумма длин всех его сторон.

Многоугольники подразделяются на треугольники — много­угольники с тремя углами (рис. 16.1, а), четырёхугольники — много­угольники с четырьмя углами (рис. 16.1, б) и т. д. Многоугольник, у которого п углов называется п-угольником.

Многоугольник называется правильным, если у него все сторо­ны равны и все углы равны (рис. 16.2).

Правильный четырёхугольник называется также квадратом.

Прямоугольникам наз ывается ч етырёхугол ьник , у к оторого все углы прямые.

Многоугольник называется выпуклым, если вместе с любыми двумя своими точками он содержит и соединяющий их отрезок (рис. 16.3).

Любой треугольник выпуклый. Среди многоугольников с чис­лом углов, большим трёх, могут быть выпуклые (рис. 16.4, а) и невы­пуклые (рис. 16.4, б).

Многоугольники могут иметь и более сложную формы. Приме­ры таких многоугольников показаны на рисунке 16.5.

Диагональю многоугольника называется отрезок, соединяю­щий его несоседние вершины (рис. 16.6).

Ясно, что выпуклый многоугольник содержит все свои диагона­ли. Невыпуклый многоугольник может не содержать некоторые свои диагонали (рис. 16.6, б).

1. На сколько частей разбивает плоскость простая замкнутая ломаная?

2. Какая фигура называется многоугольником? Что называется:

а) вершинами; б) сторонами; в) углами многоугольника?

3. Какие точки многоугольника называются внутренними?

4. Что называется периметром многоугольника?

5. Какой многоугольник называется «-угольником?

6. Какой многоугольник называется: а) правильным; 6) выпук­лым?

7. Что называется диагональю многоугольника?

8. Какой многоугольник содержит все свои диагонали?

1. Проверьте, что линия, изображённая на рисунке 16.7, является простой замкнутой ломаной. Выясните, какая из данных точек лежит:

а) внутри; 6) вне этой ломаной.

2. Укажите, какие из представленных на рисунке 16.8 фигур являются многоугольниками, а какие нет.

3. Укажите, какие из представленных на рисунке 16.9 фигур яв­ляются: а) выпуклыми многоугольниками; б) невыпуклыми много­угольниками.

4. Нарисуйте выпуклые и невыпуклые: а) четырёхугольник;

б) пятиугольник; в) шестиугольник. Используя линейку, найдите пе­риметры этих многоугольников.

5. Нарисуйте правильные треугольник, четырёхугольник, пяти­угольник и шестиугольник. Проверьте правильность нарисованных многоугольников с помощью линейки и транспортира.

6. Являются ли многоугольники, изображенные на рисунке 16.10, правильными?

7. На сколько треугольников делится выпуклый: а) четырёх­угольник; 6) пятиугольник; в) шестиугольник своими диагоналями, проведёнными из одной вершины?

8. Сколько всего диагоналей имеет: а) четырёхугольник; б) пятиугольник; в) шестиугольник; г)* n-угольник?

9. Может ли многоугольник иметь: а) одну диагональ; б) три диагонали; в) восемь диагоналей; г) десять диагоналей; д) двадцать диагоналей?

10. Существует ли многоугольник: а) число диагоналей которого равно числу его сторон; б) число диагоналей которого меньше числа его сторон; в) число диагоналей которого больше числа его сторон?

11. Выпуклый многоугольник имеет 14 диагоналей. Сколько у него сторон?

12*. На клетчатой бумаге изобразите какой-нибудь четырёх­угольник, вершинами которого являются точки АД С и D (рис. 16.11). Сколько таких четырёхугольников?

13. Изобразите два треугольника так, чтобы их общей частью был: а) треугольник; б) четырёхугольник; в) пятиугольник; г) шести­угольник.

Видео:8 класс, 3 урок, ЧетырехугольникСкачать

Четырехугольник

Видео:Многоугольники. Математика 8 класс | TutorOnlineСкачать

Определение четырехугольника

Определение 1. Четырехугольник − это замкнутая ломаная линия, состоящая из четырех звеньев.

Определение 2. Четырехугольник − геометрическая фигура (многоугольник), состоящая из четырех точек, никакие три из которых не лежат на одной прямой и последовательно соединенные четырьмя отрезками, называемыми сторонами четырехугольника.

Объединение четырехугольника и ограниченной им части плоскости также называют четырехугольником.

Любой четырехугольник разделяет плоскость на две части, одна из которых называется внутренней областью четырехугольника, а другая внешней областью четырехугольника.

Видео:Что такое выпуклый четырёхугольник? | Математика 8 класс | Геометрия 8 класс | МегаШколаСкачать

Виды четырехугольников

Четырехугольники бывают следующих видов:

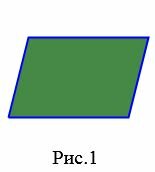
• Параллелограмм − четырехугольник, у которого противоположные стороны попарно вправны и параллельны (Рис.1).
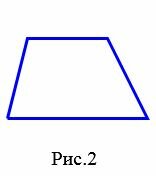
• Трапеция − четырехугольник, у которого две противоположные стороны параллельны (Рис.2).
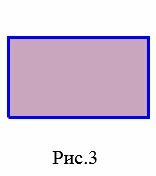
• Прямоугольник − четырехугольник, у которого все углы прямые (Рис.3).
• Ромб − четырехугольник, у которого все стороны равны (Рис.4).
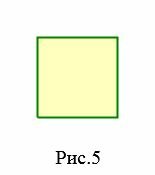
• Квадрат − четырехугольник, у которого все стороны равны и все углы прямые (Рис.5).
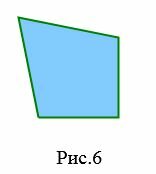
• Дельтоид − четырехугольник, у которого есть две пары равных смежных сторон (Рис.6, Рис.6.1).
• Антипараллелограмм (или контрпараллелограмм)− четырехугольник, у которого противоположные стороны равны но не параллельны (с самопересечением) (Рис.7).

Видео:Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

Обозначение четырехугольника

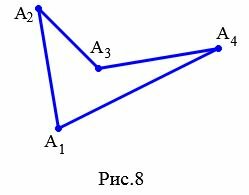
Обозначают четырехугольник буквами, стоящих при его вершинах. Называют четырехугольник чередовав буквы при его вершинах по часовой стрелке или против часовой стрелки. Например, четырехугольник на рисунке 8 называют ( small A_1A_2A_3A_4 ) или ( small A_4A_3A_2A_1 ) (Рис.8).

Видео:№363. Начертите выпуклые пятиугольник и шестиугольник. В каждом многоугольникеСкачать

Соседние вершины четырехугольника

Вершины четырехугольника называются соседними, если они являются концами одной из его сторон.

На рисунке 8 вершины ( small A_2 ) и ( small A_3 ) являются соседними, так как они являются концами стороны ( small A_2A_3. )

Видео:Чему равна сумма углов выпуклого многоугольникаСкачать

Смежные стороны четырехугольника

Стороны четырехугольника называются смежными, если они имеют общую вершину.

На рисунке 8 стороны ( small A_2A_3 ) и ( small A_3A_4 ) являются смежными, так как они имеют общую вершину ( small A_3. )

Видео:Многоугольники. 8 класс.Скачать

Простой четырехугольник. Самопересекающийся четырехугольник

Четырехугольник называется простым, если его несмежные стороны не имеют общих точек (внутренних или концевых).

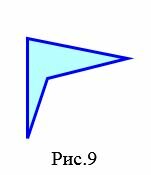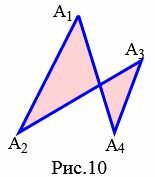На рисунках 9 и 9.1 изображены простые четырехугольники так как стороны четырехугольников не имеют самопересечений. А на рисунке 10 четырехугольник не является простым, так как стороны ( small A_1A_4 ) и ( small A_2A_3 ) пересекаются. Такой четырехугольник называется самопересекающийся.

Видео:Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

Выпуклый четырехугольник

Четырехугольник называется выпуклым, если она лежит по одну сторону от прямой, проходящей через любую его сторону.

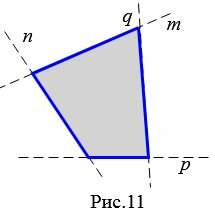На рисунке 11 четырехугольник лежит по одну сторону от прямых ( small m, n, p, q, ) проходящих через стороны четырехугольника. Поэтому такой четырехугольник выпуклый.

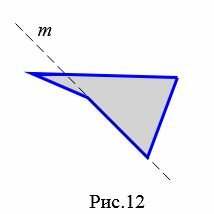На рисунке 12 прямая ( small m) делит четырехугольник на две части, т.е. четырехугольник не лежит по одну сторону от прямой ( small m). Следовательно, этот четырехугольник не является выпуклым.

Видео:SOS-ГЕОМЕТРИЯ! Отрезки и углы, смежные и вертикальные углы | Математика TutorOnlineСкачать

Правильный четырехугольник

Простой четырехугольник называется правильным, если все его стороны равны и все углы равны. Квадрат является правильным четырехугольником, так как все его стороны равны и все его углы равны 90°. Среди четырехугольников других правильных четырехугольников не существует.

На рисунке 5 изображен правильный четырехугольник (квадрат), так как у данного четырехугольника все стороны равны и все углы равны. Четырехугольник (ромб) на на рисунке 4 не является правильным, так как все стороны четырехугольника равны, но все его углы не равны друг другу. Прямоугольник также не является правильным четырехугольником, так как несмотря на то, что все углы прямоугольника равны, но все четыре стороны прямоугольника не равны друг другу.

Видео:Миникурс по геометрии. ЧетырехугольникиСкачать

Периметр четырехугольника

Сумма всех сторон четырехугольника называется периметром четырехугольника. Для четырехугольника ( small A_1A_2A_3A_4 ) периметр вычисляется из формулы:

Видео:Выпуклый многоугольник | Геометрия 7-9 класс #40 | ИнфоурокСкачать

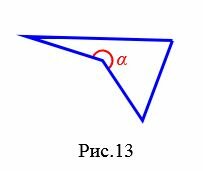
Угол четырехугольника

Углом (внутренним углом) четырехугольника при данной вершине называется угол между двумя сторонами четырехугольника, сходящимися к этой вершине. Если четырехугольник выпуклый, то все углы четырехугольника меньше 180°. Если же четырехугольник невыпуклый, то он имеет внутренний угол больше 180° (угол ( small alpha ) на рисунке 13).

Видео:Геометрия 8 класс (Урок№1 - Многоугольники. Четырёхугольник.)Скачать

Внешний угол четырехугольника

Внешним углом четырехугольника при данной вершине называется угол смежный внутреннему углу четырехугольника при данной вершине.

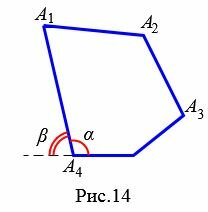На рисунке 14 угол α является внутренним углом четырехугольника при вершине ( small A_4, ) а углы β и γ являются внешними углами четырехугольника при этой же вершине. Очевидно, что при каждой вершине есть два внешних угла.

Видео:Построение пятиугольника циркулемСкачать

Диагональ четырехугольника

Диагоналями называют отрезки, соединяющие две несоседние вершины четырехугольника.

Очевидно, что у четырехугольника две диагонали.

Видео:№364. Найдите сумму углов выпуклого: а) пятиугольника; б) шестиугольника; в) десятиугольника.Скачать

Сумма углов четырехугольника

Для любого простого четырехугольника по крайней мере один диагональ делит его на два треугольника. Сумма углов треугольника равна 180°. Поэтому сумма углов простого четырехугольника равна 360°.

Видео:Как распознать талантливого математикаСкачать

Сумма внешних углов четырехугольника

Пусть задан четырехугольник ( small A_1A_2A_3A_4 .) Внешний угол при вершине ( small A_1) равен ( small 180°-angle A_1.) Аналогично, внешние углы при вершинах ( small A_2, A_3, A_4 ) равны ( small 180°-angle A_2, ) ( small 180°-angle A_3, ) ( small 180°-angle A_4, ) соответственно. Тогда сумма внешних углов четырехугольника равна:

Задача 1. Доказать, что длина любой стороны четырехугольника меньше суммы длин трех его сторон.

Решение. Рассмотрим произвольный четырехугольник ABCD (Рис.15). Покажем, например, что AB

🎬 Видео

Выпуклый четырехугольникСкачать

Четырехугольники. Вебинар | МатематикаСкачать