В настоящее время у меня есть следующая строка в моей программе. У меня есть две другие переменные целого числа, x а также y ,
Я хотел бы увидеть, если эта новая точка (x, y) на этой линии. Я искал в следующей теме:
Я придумал следующее:
Кажется, это не работает, или эта идея не подходит?
Видео:Как построить точки в системе координат OXYZСкачать

Решение
Числа с плавающей точкой имеют ограниченную точность, поэтому вы получите ошибки округления в результате вычислений, в результате чего значения, которые должны быть математически равны, в конечном итоге будут немного отличаться.
Вам нужно сравнить с небольшим допуском на ошибку:
Самое сложное — выбрать эту терпимость. Если вы не можете принять какие-либо ошибки, тогда вам нужно будет использовать что-то кроме значений с плавающей запятой фиксированной точности — возможно, целых чисел, с перестановкой вычислений, чтобы избежать деления и других неточных операций.
В любом случае, вы можете сделать это проще, без чего-либо вроде квадратного корня. Вы хотите узнать, параллельны ли два вектора; они есть, если векторное произведение равно нулю или, что эквивалентно, если они имеют равные касательные. Так что вам просто нужно
Если ваши входные данные являются целыми числами, достаточно маленькими, чтобы умножение не переполнялось, тогда арифметика с плавающей точкой вообще не нужна.
Видео:Координаты вектора. 9 класс.Скачать

Другие решения
Эффективным способом решения этой проблемы является использование области треугольника со знаком. Когда подписанная область треугольника создана точками , , а также близка к нулю, вы можете рассмотреть быть на линии. Как уже упоминали другие, выбор хорошего значения допуска является важной частью этого, если вы используете значения с плавающей запятой.
Это даст вам знать, если лежит на линии, но это не будет определять, если содержится в отрезке линии. Для этого вам также необходимо проверить против границ отрезка.
Сначала вам нужно рассчитать уравнение вашей линии. Затем посмотрите, верно ли это уравнение для значений x и y, которые у вас есть. Чтобы вычислить уравнение вашей линии, вам нужно выяснить, где она пересекает ось Y и каков ее градиент. Уравнение будет иметь вид y = mx + c, где m — градиент, а c — «перехват» (где линия пересекает ось y).
Для значений с плавающей запятой не используйте ==, но вместо этого проверьте небольшую разницу:
Кроме того, вам не нужен единичный вектор, только тангенс:
(дельта должно быть небольшое число, которое зависит от точности, которую вы ожидаете.)
Учитывая, что (x, y) на самом деле точка, задание кажется немного проще, чем вы его делаете.
Вы, вероятно, хотите начать с проверки идеально горизонтальной или вертикальной линии. В этих случаях вы просто проверяете, x падает между x1 а также x2 (или же y между y1 а также y2 для вертикали).
В противном случае вы можете использовать линейную интерполяцию на x и посмотрите, дает ли оно правильное значение для y (в пределах некоторого возможного допуска для округления). Для этого вы должны сделать что-то вроде:
Видео:Координаты точки и координаты вектора 1.Скачать

Урок 31. Проверка принадлежности точки отрезку
Урок из серии «Геометрические алгоритмы»
Здравствуйте, дорогой читатель!
Сегодня мы рассмотрим еще одну типовую задачу из серии геометрические алгоритмы. Напишем функцию, которая будет проверять принадлежность произвольной точки отрезку, заданному координатами своего начала и конца.
Для реализации операций сравнения над вещественными данными напишем еще две функции: функцию EqPoint(), которая ,будет проверять, совпадают ли две точки на плоскости и функцию RealMoreEq() , которую будем использовать для проверки отношения «>=» (больше или равно). Причина ввода специальных функций нам уже известна.
Задача. Проверить, принадлежит ли точка отрезку.
Пусть точки 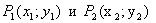
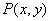
Вектор с началом в точке 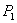
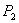
Если P(x, y) – произвольная точка, то координаты вектора 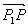
Точка Р будет принадлежать отрезку если:
- Векторы в
и
коллинеарны (равно нулю их векторное произведение):
, т.е. (x-x1)(y2-y1)-(y-y1)(x2-x1) = 0
- Абсцисса точки P удовлетворяет условию:
или
. Иначе точка будет находиться на прямой левее или правее отрезка.
Результаты выполнения программы.
Введите координаты точек: x1, y1, x2, y2, x,y
0.5 1 2.5 2.8 1.203 1.633
Да.
Видео:№362. Точка К — середина ребра ВС тетраэдра ABCD. Разложите вектор DK по векторамСкачать

Вычислительная геометрия, или как я стал заниматься олимпиадным программированием. Часть 2
Вступление
Это вторая часть моей статьи посвящена вычислительной геометрии. Думаю, эта статья будет интереснее предыдущей, поскольку задачки будут чуть сложнее.
Начнем с взаимного расположения точки относительно прямой, луча и отрезка.
Задача №1
Определить взаимное расположении точки и прямой: лежит выше прямой, на прямой, под прямой.
Решение
Понятно, что если прямая задана своим уравнением ax + by + c = 0, то тут и решать нечего. Достаточно подставить координаты точки в уравнение прямой и проверить чему оно равно. Если больше нуля, то точка находится в верхней полуплоскости, если равна нулю, то точка находится на прямой и если меньше нуля, то точка находится в нижней полуплоскости. Интереснее случай, когда прямая задана, задана координатами двух точек назовем их P1(x1, y1), P2(x2, y2). В этом случае можно спокойно найти коэффициенты a, b и c и применить предыдущее рассуждение. Но надо сначала подумать, оно нам надо? Конечно, нет! Как я говорил косое произведения — это просто жемчужина вычислительной геометрии. Давайте применим его. Известно, что косое произведение двух векторов положительно, если поворот от первого вектора ко второму идет против часовой стрелки, равно нулю, если векторы коллинеарны и отрицательно, если поворот идет по часовой стрелки. Поэтому нам достаточно посчитать косое произведение векторов P1P2 и P1M и по его знаку сделать вывод.
Задача №2
Определить принадлежит ли точка лучу.
Решение
Давайте вспомним, что такое луч: луч — это прямая, ограниченная точкой с одной стороны, а с другой стороны бесконечная. То есть луч задается некоторой начальной точкой и любой точкой лежащей на нем. Пусть точка P1(x1, y1) — начало луча, а P2(x2, y2) — любая точка принадлежащая лучу. Понятно, что если точка принадлежит лучу, то она принадлежит и прямой проходящей через эти точки, но не наоборот. Поэтому принадлежность прямой является необходимым, но не достаточным условием для принадлежности лучу. Поэтому от проверки косового произведения нам никуда не деться. Для достаточного условия нужно вычислить еще и скалярное произведение тех же векторов. Если оно меньше нуля, то точка не принадлежит лучу, если же оно не отрицательно, то точка лежит на луче. Почему так? Давайте посмотрим на рисунок.
Итак, для того чтобы точка M(x, y) лежала на луче с начальной точкой P1(x1, y1), где P2(x2, y2) лежит на луче необходимо и достаточно выполнения двух условий:
1. [P1P2, P1M] = 0 – косое произведение (точка лежит на прямой)
2. (P1P2, P1M) ≥ 0 – скалярное произведение (точка лежит на луче)
Задача №3
Определить принадлежит ли точка отрезку.
Решение
Пусть точки P1(x1, y1), P2(x2, y2) концы заданного отрезка. Опять-таки необходимым условием принадлежности точки отрезку является ее принадлежность прямой проходящей через P1, P2. Далее нам нужно определить лежит ли точка между точками P1 и P2, для этого нам на помощь приходит скалярное произведение векторов только на этот раз других: (MP1, MP2). Если оно меньше либо равно нуля, то точка лежит на отрезке, иначе вне отрезка. Почему так? Посмотрим на рисунок.
Итак, для того чтобы точка M(x, y) лежала на отрезке с концами P1(x1, y1), P2(x2, y2) необходимо и достаточно выполнения условий:
1. [P1P2, P1M] = 0 – косое произведение (точка лежит на прямой)
2. (MP1,MP2) ≤ 0 – скалярное произведение (точка лежит между P1 и P2)
Задача №4
Взаимное расположение двух точек относительно прямой.
Решение
В этой задаче необходимо определить по одну или по разные стороны относительно прямой находятся две точки.
Если точки находятся по разные стороны относительно прямой, то косые произведения имеют разные знаки, а значит их произведение отрицательно. Если же точки лежат по одну сторону относительно прямой, то знаки косых произведений совпадают, значит, их произведение положительно.
Итак:
1. [P1P2, P1M1] * [P1P2, P1M2] 0 – точки лежат по одну сторону.
3. [P1P2, P1M1] * [P1P2, P1M2] = 0 – одна (или две) из точек лежит на прямой.
Кстати, задача об определении наличия точки пересечения у прямой и отрезка решается точно также. Точнее, это и есть эта же задача: отрезок и прямая пересекаются, когда концы отрезка находятся по разные стороны относительно прямой или когда концы отрезка лежат на прямой, то есть необходимо потребовать [P1P2, P1M1] * [P1P2, P1M2] ≤ 0.
Задача №5
Определить пересекаются ли две прямые.
Решение
Будем считать, что прямые не совпадают. Понятно, что прямые не пересекаются, только если они параллельны. Поэтому, найдя условие параллельности, мы можем, определить пересекаются ли прямые.
Допустим прямые заданы своими уравнениями a1x + b1y + c1 = 0 и a2x + b2y + c2 = 0. Тогда условие параллельности прямых заключается в том, что a1b2 — a2b1 = 0.
Если же прямые заданы точками P1(x1, y1), P2(x2, y2), M1(x3, y3), M2(x4, y4), то условие их параллельности заключается в проверки косого произведения векторов P1P2 и M1M2: если оно равно нулю, то прямые параллельны.
В общем, то когда прямые заданы своими уравнениями мы тоже проверяем косое произведение векторов (-b1, a1), (-b2, a2) которые называются направляющими векторами.
Задача №6
Определить пересекаются ли два отрезка.
Решение
Вот эта задача мне, действительно, нравится. Отрезки пересекаются тогда, когда, концы каждого отрезка лежат по разные стороны от другого отрезка. Посмотрим на рисунок:
Итак, нам нужно проверить, чтобы концы каждого из отрезков лежали по разные стороны относительного концов другого отрезка. Пользуемся косым произведением векторов. Посмотрите на первый рисунок: [P1P2, P1M2] > 0, [P1P2, P1M1] [P1P2, P1M2] * [P1P2, P1M1] 2 + b 2 ).
Задача №8
Расстояние от точки до луча.
Решение
Эта задача отличается от предыдущей тем, что в этом случае может получиться, так что перпендикуляр из точки не падает на луч, а падает на его продолжение.
В случае, когда перпендикуляр не падает на луч необходимо найти расстояние от точки до начала луча – это и будет ответом на задачу.
Как же определить падает ли перпендикуляр на луч или нет? Если перпендикуляр не падает на луч, то угол MP1P2 – тупой иначе острый (прямой). Поэтому по знаку скалярного произведения векторов мы можем определить попадает ли перпендикуляр на луч или нет:
1. (P1M, P1P2) 2 .
Теперь рассмотрим случай, когда центр второго круга O2 находится между точками O1 и C. В этом случае получим отрицательное значение величины d2. Использование отрицательного значения d2 приводит к отрицательному значению α. В этом случае необходимо для правильного ответа прибавить к α 2π.
Заключение
Ну вот и все. Мы рассмотрели не все, но наиболее часто встречаемые задачи вычислительной геометрии касающиеся взаимного расположения объектов.
🎦 Видео
33 Задача: Принадлежит ли точка кругу с центром в начале координат?Скачать

Точка, прямая и отрезок. 1 часть. 7 класс.Скачать

Нахождение координат вектора. Практическая часть. 9 класс.Скачать

Построение проекции вектора на осьСкачать

11 класс, 1 урок, Прямоугольная система координат в пространствеСкачать

9 класс. Контрольная №1 (из 6). Тема: Векторы. Подробное решение с объяснением. Пробуем свои силы!Скачать

Математика без Ху!ни. Смешанное произведение векторовСкачать

Нахождение длины вектора через координаты. Практическая часть. 9 класс.Скачать

Геометрия 9 Откладывание вектора от данной точкиСкачать

Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Координаты вектора в пространстве. 11 класс.Скачать

В какой четверти находится точка единичной окружности, полученная при повороте Ро(1;0) на угол...Скачать

№783. Точка М лежит на стороне ВС параллелограмма ABCD, причем ВМ:МС=3:1. ВыразитеСкачать

8 класс, 42 урок, Откладывание вектора от данной точкиСкачать

Прямоугольная система координат в пространстве. Практическая часть. 11 класс.Скачать

Доказать, что точки лежат в одной плоскости - bezbotvyСкачать

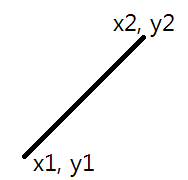
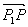 и
и 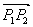 коллинеарны (равно нулю их векторное произведение):
коллинеарны (равно нулю их векторное произведение): 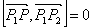 , т.е. (x-x1)(y2-y1)-(y-y1)(x2-x1) = 0
, т.е. (x-x1)(y2-y1)-(y-y1)(x2-x1) = 0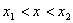 или
или 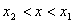 . Иначе точка будет находиться на прямой левее или правее отрезка.
. Иначе точка будет находиться на прямой левее или правее отрезка.