На сторонах выпуклого четырехугольника отмечены точки так что

Видео:№380. На сторонах АВ, ВС, CD и DA четырехугольника ABCD отмечены соответственно точки М, N, Р и QСкачать

Ваш ответ

Видео:№28. На сторонах АВ и АС треугольника ABC взяты соответственноСкачать

решение вопроса

Видео:В треугольнике ABC на сторонах АВ и ВС отмечены точки М и К соответственно, ВМ/АВ = 1/2, ВК/ВС = 4/5Скачать

Похожие вопросы

• Все категории
• экономические 43,277
• гуманитарные 33,618
• юридические 17,900
• школьный раздел 606,688
• разное 16,822

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.

Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.

Видео:№479. Точки D и Е лежат на сторонах АВ и АС треугольника ABC. Найдите:Скачать

На сторонах AB, BC, CD и DA четырехугольника ABCD отмечены соответственные точки M N P и Q так что, AM = СP, BN = DQ, BM = DP, NC = QA?

Геометрия | 5 — 9 классы

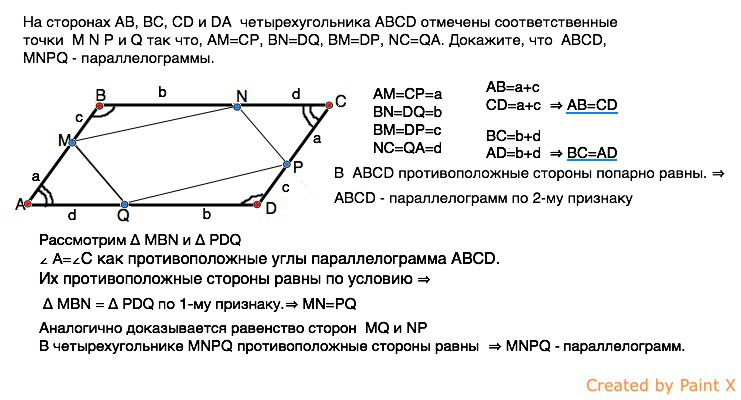
На сторонах AB, BC, CD и DA четырехугольника ABCD отмечены соответственные точки M N P и Q так что, AM = СP, BN = DQ, BM = DP, NC = QA.

Докажите, что ABCD, MNPQ — параллелограммы.

На сторонах AB, BC, CD и DA четырехугольника ABCD отмечены соответственные точки M N P и Q так что, AM = СP, BN = DQ, BM = DP, NC = QA.

Докажите, чтоABCD, MNPQ — параллелограммы.

Обозначим равные отрезки одинаковыми буквами :

СD = a + c ⇒ AB = CD

AD = b + d ⇒ BC = AD

В четырехугольнике АВСD противоположные стороны попарно равны.

АВСD — параллелограмм ( 2 — й признак)

Рассмотрим ∆ MBN и ∆ PDQ

∠А = ∠С как противоположные углы параллелограмма АВСD.

Содержащие эти углы стороны равны по условию⇒

∆ MBN = ∆ PDQ по 1 — му признаку.

Аналогично доказывается равенство сторон MQ и NP

В четырехугольнике MNРQ противоположные стороны равны⇒MNРQ — параллелограмм.

Видео:8 класс, 3 урок, ЧетырехугольникСкачать

В параллелограмме ABCD на сторонах AB, BC, CD, DA отмечены точки E, F, P, Q, причем AE / AB = BF / BC = СР / CD = DQ / DA = 1 / 3?

В параллелограмме ABCD на сторонах AB, BC, CD, DA отмечены точки E, F, P, Q, причем AE / AB = BF / BC = СР / CD = DQ / DA = 1 / 3.

Докажите, что EFQP — параллелограмм.

Видео:№368. Найдите углы выпуклого четырехугольника, если они равны друг другу.Скачать

В паралелограмме ABCD точки E — середина сторон BC и AD соответсвенно?

В паралелограмме ABCD точки E — середина сторон BC и AD соответсвенно.

Докажите что четырехугольник AECK — ПАРАЛЛЕЛОГРАММ.

Видео:Геометрия На сторонах AB и BC треугольника ABC отмечены соответственно точки M и K так, что AM = 3BMСкачать

ДАЮ 60 БАЛЛОВ?

Через точку пересечения диагоналей параллелограмма ABCD проведены две прямые.

Одна из них пересекает стороны AB и CD, соответственно, в точках М и К, вторая — стороны BC и AD, соответственно, в точках N и L.

Докажите, что четырехугольник MNKL — параллелограмм.

Видео:№369. Найдите углы A, B и C выпуклого четырехугольника ABCD, еслиСкачать

Сторона bc параллелограмма abcd вдвое больше стороны ab?

Сторона bc параллелограмма abcd вдвое больше стороны ab.

Точка E — середина стороны BC.

Докажите, что AE — биссектриса угла BAD.

Видео:№118. На основании ВС равнобедренного треугольника ABC отмечены точки М и N так, что BM=CN. ДокажитеСкачать

На сторонах AB, BC, CD, DA четырёхугольника ABCD отмечены соответственно точки M, N, P, Q так, что AM = CP, BN = DQ, BM = DP, NC = QA?

На сторонах AB, BC, CD, DA четырёхугольника ABCD отмечены соответственно точки M, N, P, Q так, что AM = CP, BN = DQ, BM = DP, NC = QA.

Докажите, что ABCD и MNPQ — — — ПАРАЛЛЕЛОГРАММЫ.

Видео:Геометрия На сторонах AC и BC треугольника ABC отметили точки M и K так, что CM = 15 см, CK = 12 смСкачать

Сторона ab параллелограмма abcd вдвое больше стороны bc точка N середина стороны ab докажите что cn биссектриса угла bcd?

Сторона ab параллелограмма abcd вдвое больше стороны bc точка N середина стороны ab докажите что cn биссектриса угла bcd.

Видео:№383 На диагонали BD параллелограмма ABCD отмечены две точки Р и Q так, что PB=QD. ДокажитеСкачать

На стороне BC параллелограмма ABCD взята точка M так, что AB = BM?

На стороне BC параллелограмма ABCD взята точка M так, что AB = BM.

Докажите, что AM — биссектриса угла BAD.

Видео:№370. Найдите углы выпуклого четырехугольника, если они пропорциональны числам 1, 2, 4, 5.Скачать

На стороне bc выпуклого четырехугольника abcd отмечена точка p, а вне четырёхугольника — точка Q?

На стороне bc выпуклого четырехугольника abcd отмечена точка p, а вне четырёхугольника — точка Q.

При этом отрезки BP и AQ, а также CP и DQ имеют общие середины.

Докажите что отрезки AC и BD имеют общую середину.

Видео:Задача №255 [НЕДЕТСКАЯ ГЕОМЕТРИЯ #1]Скачать

В параллелограмме ABCD точки E и К середины сторон BC и AD соответственно?

В параллелограмме ABCD точки E и К середины сторон BC и AD соответственно.

Докажите, что четырехугольник ABEK параллелограмм.

Видео:#8warmup. Разбор восьмой разминкиСкачать

В четырехугольнике ABCD точки M, N, P, Q соответственно середины сторон AB, BC, CD, DA, докажите, что отрезки MP и NQ точкой пересечения делятся пополам?

В четырехугольнике ABCD точки M, N, P, Q соответственно середины сторон AB, BC, CD, DA, докажите, что отрезки MP и NQ точкой пересечения делятся пополам.

На этой странице находится вопрос На сторонах AB, BC, CD и DA четырехугольника ABCD отмечены соответственные точки M N P и Q так что, AM = СP, BN = DQ, BM = DP, NC = QA?. Здесь же – ответы на него, и похожие вопросы в категории Геометрия, которые можно найти с помощью простой в использовании поисковой системы. Уровень сложности вопроса соответствует уровню подготовки учащихся 5 — 9 классов. В комментариях, оставленных ниже, ознакомьтесь с вариантами ответов посетителей страницы. С ними можно обсудить тему вопроса в режиме on-line. Если ни один из предложенных ответов не устраивает, сформулируйте новый вопрос в поисковой строке, расположенной вверху, и нажмите кнопку.

15″ = 10″ + х» х» = 15″ — 10″ х = 5 S = 1 / 2 высоты * на сторону, к которой она проведена S = 1 / 2 * 5 * 10 S = 25 см2 » — квадрат ( 15″ — 15 в квадрате).

Дано : АВС , АВ = ВС = 15 см АС = 10Найти : S — ? Решение : Высота, опущенная из вершины равнобедренного треугольника на его основание является одновременно и высотой, и медианой. ВН — высотаАН = НС = 5 смТреугольник АВН — прямоугольный, катет АН =..

Только если в общем виде , если будет. Дан угол прорстро получать и посчитай.

Ииосноваа Х сотая ле врмпо флтсяаходции аходции адь трапплощадей.

DOA по двум углам (накрест лежащим) , BO : OD = OC : AO = BC : AD = 2 : 3 2AO = 3OC AO + OC = 20 2AO + 2OC = 40 5OC = 40 OC = 8 AO = 12.

OB = OA, OC = CO(общая сторона), AC = BC.

1)тр. АОС = тр. ОСВ (по двум катетам) = > АС = ВС(соотв. Элементы).

Держи . Вроде так правильно.

10 дм — 100 см. Провоим высоту, она делит оснеование на две равные части, значит кусочек в равнобедренном треугольнике равен 6. По теореме пифагора находим высоту. Она равна 8. Площадь равна полупроизведение основания на высоту. 12 * 8 и делим н..

Видео:Что такое выпуклый четырёхугольник? | Математика 8 класс | Геометрия 8 класс | МегаШколаСкачать

На сторонах выпуклого четырехугольника отмечены точки так что

Загрузка решений доступна для зарегистрировавшихся пользователей

Прямая, параллельная основаниям BC и AD трапеции ABCD, пересекает боковые стороны AB и CD в точках M и N. Диагонали AC и BD пересекаются в точке O. Прямая MN пересекает стороны OA и OD треугольника AOD в точках K и L соответственно.

а) Докажите, что MK = NL.

б) Найдите MN, если известно, что BC = 3, AD = 8 и MK : KL = 1 : 3.

Загрузка решений доступна для зарегистрировавшихся пользователей

В выпуклом четырехугольнике KLMN точки A, B, C, D — середины сторон KL, LM, MN, NK соответственно. Известно, что KL = 3. Отрезки AC и BD пересекаются в точке O. Площади четырехугольников KAOD, LAOB и NDOC равны соответственно 6, 6 и 9.

а) Докажите, что площади четырехугольников MCOB и NDOC равны.

б) Найдите длину отрезка MN.

Загрузка решений доступна для зарегистрировавшихся пользователей

В трапеции ABCD AD и BC — основания, O — точка пересечения диагоналей.

а) Докажите, что выполняется равенство

б) Найдите площадь трапеции ABCD, если

Загрузка решений доступна для зарегистрировавшихся пользователей

Дан квадрат ABCD со стороной 7. На сторонах BC и CD даны точки M и N такие, что периметр треугольника CMN равен 14.

а) Докажите, что B и D — точки касания вневписанной окружности треугольника CMN, а её центр находится на вершине A квадрата ABCD.

б) Найдите угол MAN.

Загрузка решений доступна для зарегистрировавшихся пользователей

В выпуклом пятиугольнике ABCDE диагонали BE и CE являются биссектрисами углов при вершинах B и C соответственно.

а) Докажите, что точка E есть центр вневписанной окружности для треугольников OCB, где O — точка пересечения прямых CD и AB.

б) Найдите площадь пятиугольника ABCDE, если угол A равен 35°, угол D равен 145°, а площадь треугольника BCE равна 11.

Загрузка решений доступна для зарегистрировавшихся пользователей

В параллелограмме ABCDдиагонали пересекаются в точке О, длина диагонали BD равна 12. Расстояние между центрами окружностей, описанных около треугольников AOD и COD, равно 16. Радиус окружности, описанной около треугольника AOB, равен 5. Найти площадь параллелограмма ABCD.

Загрузка решений доступна для зарегистрировавшихся пользователей

Через вершину C квадрата ABCD проведена прямая, пересекающая диагональ BD в точке K, а серединный перпендикуляр к стороне AB — в точке M. Найдите если

Загрузка решений доступна для зарегистрировавшихся пользователей

Продолжения сторон AD и BC выпуклого четырехугольника ABCD пересекаются в точке M, а продолжения сторон AB и CD — в точке O. Отрезок MO перпендикулярен биссектрисе угла AOD. Найдите отношение площадей треугольника AOD и четырехугольника ABCD, если OA = 12, OD = 8, CD = 2.

Загрузка решений доступна для зарегистрировавшихся пользователей

В параллелограмме ABCD биссектрисы углов при стороне AD делят сторону BC точками M и N так, что Найдите BC, если AB = 12.

Загрузка решений доступна для зарегистрировавшихся пользователей

В трапеции KLMN известны боковые стороны KL = 36, MN = 34, верхнее основание LM = 10 и Найдите диагональ LN.

Загрузка решений доступна для зарегистрировавшихся пользователей

Диагонали AC и BD трапеции ABCD пересекаются в точке Е. Найти площадь трапеции, если площадь треугольника AED равна 9, а точка Е делит одну из диагоналей в отношении 1 : 3.

Загрузка решений доступна для зарегистрировавшихся пользователей

Площадь равнобедренной трапеции равна Угол между диагональю и основанием на 20 градусов больше угла между диагональю и боковой стороной. Найдите острый угол трапеции, если ее диагональ равна 2.

Загрузка решений доступна для зарегистрировавшихся пользователей

Дан параллелограмм ABCD. Точка M лежит на диагонали BD и делит ее в отношении 2 : 3. Найдите площадь параллелограмма ABCD, если площадь четырехугольника ABCM равна 60.

Загрузка решений доступна для зарегистрировавшихся пользователей

Периметр трапеции равен 112. Точка касания вписанной в трапецию окружности делит одну из боковых сторон на отрезки, равные 8 и 18. Найдите основания этой трапеции.

Загрузка решений доступна для зарегистрировавшихся пользователей

В ромбе ABCD со стороной 2 и углом 60° проведены высоты CM и DK. Найдите длину отрезка MK.

Загрузка решений доступна для зарегистрировавшихся пользователей

Диагонали трапеции равны 13 и а высота равна 5. Найдите площадь трапеции.

Загрузка решений доступна для зарегистрировавшихся пользователей

На стороне CD квадрата ABCD построен равносторонний треугольник CPD. Найдите высоту треугольника ADP, проведённую из вершины D, если известно, что сторона квадрата равна 1.

Загрузка решений доступна для зарегистрировавшихся пользователей

В трапеции ABCD ВС и AD — основания. Биссектриса угла А пересекает сторону CD в ее середине — точке Р.

а) Докажите, что ВР – биссектриса угла АВС.

б) Найдите площадь трапеции ABCD, если известно, что AP = 8, BP = 6.

Загрузка решений доступна для зарегистрировавшихся пользователей

Точка E — середина стороны AD параллелограмма ABCD, прямые BE и АС взаимно перпендикулярны и пересекаются в точке О.

а) Докажите, что площади треугольников АОВ и СОЕ равны.

б) Найдите площадь параллелограмма ABCD, если AB = 3, BC = 4.

Загрузка решений доступна для зарегистрировавшихся пользователей

Пусть О — точка пересечения диагоналей выпуклого четырехугольника ABCD. Периметры треугольников AOB, BOC, COD и DOА равны между собой.

А) Докажите, что в четырехугольник ABCD можно вписать окружность.

Б) Найдите радиус окружности, вписанной в треугольник DOA, если радиусы окружностей, вписанных в треугольники AOB, BOC и COD равны соответственно 3, 4 и 6.

Загрузка решений доступна для зарегистрировавшихся пользователей

Диагонали равнобокой трапеции ABCD пересекаются под прямым углом. ВН — высота к большему основанию CD, EF — средняя линия трапеции.

а) Докажите, что BH = DH.

б) Найдите площадь трапеции, если EF = 5.

Загрузка решений доступна для зарегистрировавшихся пользователей

Трапеция ABCD с углами при одном основании и описана около круга.

а) Докажите, что отношение площади трапеции к площади круга выражается формулой

б) Найдите площадь прямоугольной трапеции ABCD, если а площадь вписанного круга равна

Загрузка решений доступна для зарегистрировавшихся пользователей

Прямая p, параллельная основаниям BC и AD трапеции ABCD, пересекает прямые AB, AC, BD и CD в точках E, F, G и H соответственно, причём EF = FG.

а) Докажите, что точки пересечения прямой p с диагоналями AC и BD делят отрезок EН на три равных части;

б) Найдите EF, если BC = 3, AD = 4.

Загрузка решений доступна для зарегистрировавшихся пользователей

В трапеции параллельно основаниям проведены четыре отрезка с концами на боковых сторонах: KL, MN, RS и TQ. Известно, что первый отрезок проходит через точку пересечения диагоналей трапеции, второй — делит ее на два подобных четырехугольника, третий — соединяет середины боковых сторон, четвертый разбивает трапецию на две равновеликие части.

а) Найдите длины этих отрезков.

б) Докажите, что KL

Загрузка решений доступна для зарегистрировавшихся пользователей

В равнобокой описанной трапеции ABCD, где угол B тупой, а BC и AD — основания, проведены: 1) биссектриса угла B; 2) высота из вершины С; 3) прямая, параллельная AB и проходящая через середину отрезка CD.

а) Докажите, что все они пересекаются в одной точке.

б) Найдите расстояние между центрами вписанной и описанной окружностей трапеции ABCD, если известно, что BC = 8, AD = 18.

Загрузка решений доступна для зарегистрировавшихся пользователей

В трапеции ABCD площадью, равной 30, диагонали АС и BD взаимно перпендикулярны, а ∠BAC = ∠CDB. Продолжения боковых сторон AB и CD пересекаются в точке K.

А) Докажите, что трапеция ABCD — равнобедренная.

Б) Найдите площадь треугольника AD, если известно, что ∠ AKD=30°, а BC

Загрузка решений доступна для зарегистрировавшихся пользователей

В четырехугольник ABCD биссектриса угла С пересекает сторону AD в точке M, а биссектриса угла А пересекает сторону BC в точке K. Известно, что AKCM — параллелограмм.

а) Докажите, что ABCD — параллелограмм.

б) Найдите площадь четырехугольника ABCD, если BK = 3, AM = 2, а угол между диагоналями AC и BD равен 60°.

Загрузка решений доступна для зарегистрировавшихся пользователей

В параллелограмме (отличном от ромба) проведены биссектрисы четырех углов.

А) Докажите, что в четырехугольнике, ограниченном биссектрисами, диагонали равны.

Б) Найдите площадь четырехугольника, ограниченного биссектрисами, если известно, что стороны параллелограмма равны 3 и 5 , а угол параллелограмма равен 60°.

Загрузка решений доступна для зарегистрировавшихся пользователей

В выпуклом четырехугольнике ABCD диагонали AC и BD пересекаются в точке О. Площади треугольников AOB и COD равны.

а) Докажите, что точки A и D одинаково удалены от прямой ВС.

б) Найдите площадь треугольника AOB, если известно, что AB = 13, BC = 10, CD = 15, DA = 24.

Загрузка решений доступна для зарегистрировавшихся пользователей

На сторонах AD и BC параллелограмма AВCD взяты соответственно точки M и N, причем ВN : NC = 1 : 3. Оказалось, что прямые AN и АС разделили отрезок BM на три равные части.

а) Докажите, что точка M — середина стороны АD параллелограмма.

б) Найдите площадь параллелограмма ABCD, если известно, что площадь четырехугольника, ограниченного прямыми АN, AС, BM и BD равна 16.

Загрузка решений доступна для зарегистрировавшихся пользователей

В выпуклом четырёхугольнике ABCD точки K, M, P, E — середины сторон AB, BC, CD, и DA соответственно.

а) Докажите, что площадь четырёхугольника KMPE равна половине площади четырёхугольника ABCD.

б) Найдите большую диагональ четырёхугольника KMPE, если известно, что AC = 6, BD = 8, а сумма площадей треугольников AKE и CMP равна

Загрузка решений доступна для зарегистрировавшихся пользователей

В параллелограмме АВСD диагональ ВD равна стороне AD.

а) Докажите, что прямая СD касается окружности ω, описанной около треугольника АВD.

б) Пусть прямая СВ вторично пересекает ω в точке К. Найдите КD : AC при условии, что угол ВDA равен

Загрузка решений доступна для зарегистрировавшихся пользователей

Дана трапеция ABCD с основаниями АD и BС. Окружности, построенные на боковых сторонах этой трапеции, как на диаметрах, пересекаются в точках Р и К.

а) Докажите, что прямые РК и ВС перпендикулярны.

б) Найдите длину отрезка РК, если известно, что АD = 20, BC = 6, AB = 16, DC = 14.

Загрузка решений доступна для зарегистрировавшихся пользователей

Диагонали АС и СЕ правильного шестиугольника ABCDEF разделены точками M и N так, что АМ : АС = СN : СЕ и точки В, М и N лежат на одной прямой.

а) Докажите, что точки В, О, N и D лежат на одной окружности (точка О — центр шестиугольника).

б) Найдите отношение АМ : АС.

Загрузка решений доступна для зарегистрировавшихся пользователей

В параллелограмме ABCD точка Е — середина стороны АD. Отрезок ВЕ пересекает диагональ АС в точке Р, АB = PD.

а) Докажите, что отрезок ВЕ перпендикулярен диагонали АС.

б) Найдите площадь параллелограмма, если АВ = 2 см, ВС = 3 см.

Загрузка решений доступна для зарегистрировавшихся пользователей

В остроугольном треугольнике АВС проведены высоты АК, ВМ и СN. На стороне АВ выбрана точка Р так, что окружность описанная около треугольника РКМ касается стороны АВ.

а) Докажите, что угол КАМ равен углу МВС.

б) Найдите РN, если РА = 30, РВ = 10.

Загрузка решений доступна для зарегистрировавшихся пользователей

Точка E — середина боковой стороны CD трапеции ABCD. На стороне AB взяли точку K так, что прямые CK и AE параллельны. Отрезки CK и BE пересекаются в точке O.

а) Докажите, что CO = KO.

б) Найдите отношение оснований трапеции BC и AD, если площадь треугольника BCK составляет 0,09 площади трапеции ABCD.

Загрузка решений доступна для зарегистрировавшихся пользователей

В равнобедренной трапеции ABCD основание AD в два раза больше основания BC.

а) Докажите, что высота CH трапеции разбивает основание AD на отрезки, один из которых втрое больше другого.

б) Пусть O — точка пересечения диагоналей трапеции ABCD. Найдите расстояние от вершины C до середины отрезка OD, если BC = 16 и AB = 10.

Загрузка решений доступна для зарегистрировавшихся пользователей

а) Докажите, что сумма углов А, В, С, D, E в вершинах произвольной 5‐конечной везды равна 180° (рис.1).

б) Найдите площадь 5‐конечной звезды, вершины которой совпадают с пятью вершинами правильного шестиугольника, если известно, что сторона последнего равна 6 (рис. 2).

Загрузка решений доступна для зарегистрировавшихся пользователей

В треугольнике АВС точка М — середина АС.

а) Докажите, что длина отрезка ВМ больше полуразности, но меньше полусуммы длин сторон АВ и ВС.

б) Окружность проходит через точки В, С, М. Найдите хорду этой окружности, лежащую на прямой АВ, если известно, что АВ = 5, ВС = 3, ВМ = 2.

Загрузка решений доступна для зарегистрировавшихся пользователей

В трапеции ABCD BC||AD, Прямая, перпендикулярная

стороне CD, пересекает сторону АВ в точке М, а сторону CD — в точке N.

а) Докажите подобие треугольников АВN и DCM

б) Найдите расстояние от точки А до прямой ВN, если МС = 5, ВN = 3, а расстояние от точки D до прямой МС равно 6.

Загрузка решений доступна для зарегистрировавшихся пользователей

Два борта бильярдного стола образуют угол 7°, как указано на рисунке. На столе лежит бильярдный шар A, который катится без трения в сторону одного из бортов под углом 113°. Отражения от бортов абсолютно упругие. Сколько раз шар отразится от бортов?

Загрузка решений доступна для зарегистрировавшихся пользователей

На стороне BC треугольника ABC отмечена K точка так, что AK = 4, ВК = 9, КС = 3. Около треугольника ABK описана окружность. Через точку C и середину D стороны AB проведена прямая, которая пересекает окружность в точке P, причем CP > CD и

а) Докажите подобие треугольников АВС и АКС;

Загрузка решений доступна для зарегистрировавшихся пользователей

Площадь трапеции ABCD равна 30. Точка Р — середина боковой стороны АВ. Точка R на боковой стороне CD выбрана так, что 2CD = 3RD. Прямые AR и PD пересекаются в точке Q, AD = 2BC.

а) Докажите, что точка Q — середина отрезка AR

б) Найдите площадь треугольника APQ.

Загрузка решений доступна для зарегистрировавшихся пользователей

Дан прямоугольник ABCD. Окружность с центром в точке В и радиусом АВ пересекает продолжение стороны АВ в точке М. Прямая МС пересекает прямую AD в точке К, а окружность во второй раз в точке F.

а) Докажите, что DK = DF.

б) Найдите КС, если BF = 20, DF = 21.

Загрузка решений доступна для зарегистрировавшихся пользователей

На стороне ВС треугольника АВС отмечена точка К. Оказалось, что отрезок АК пересекает медиану ВD в точке Е так, что АЕ = ВС.

а) Докажите, что ВК = КE.

б) Найдите площадь четырехугольника CDEК, если известно, что АВ = 13, АЕ = 7, АD = 4.

Загрузка решений доступна для зарегистрировавшихся пользователей

В четырехугольнике ABCD диагонали AC и BD пересекаются в точке K. Точки L и M являются соответственно серединами сторон BC и AD. Отрезок LM содержит точку K. Четырехугольник ABCD таков, что в него можно вписать окружность.

а) Докажите, что четырехугольник ABCD трапеция.

б) Найдите радиус этой окружности, если и

Загрузка решений доступна для зарегистрировавшихся пользователей

В четырехугольнике ABCD через каждую его вершину проведена прямая, проходящая через центр вписанной в него окружности. Три из этих прямых обладают тем свойством, что каждая из них делит площадь четырехугольника на две равновеликие части.

а) Докажите, что и четвертая прямая обладает тем же свойством.

б) Какие значения могут принимать углы этого четырехугольника, если один из них равен 108°?

Загрузка решений доступна для зарегистрировавшихся пользователей

Точка N делит диагональ трапеции ABCD в отношении Длины оснований BC и AD относятся как Через точку N и вершину D проведена прямая, пересекающая боковую сторону AB в точке M.

а) Какую часть площади трапеции составляет площадь четырехугольника MBCN?

б) Найдите длину отрезка MN, если

Загрузка решений доступна для зарегистрировавшихся пользователей

Точки K и L являются серединами боковых сторон AB и BC равнобедренного треугольника ABC. Точка M расположена на медиане AL так, что Окружность ω с центром в точке M касается прямой AC и пересекает прямую KL в точках P и Q,

а) Найти радиус окружности ω.

б) Найти периметр треугольника ABC.

Загрузка решений доступна для зарегистрировавшихся пользователей

Внутри параллелограмма ABCD взята точка K так, что треугольник CKD равносторонний. Известно, что расстояния от точки K до прямых AD, AB и BC равны соответственно 3, 6 и 5.

а) Найдите площадь параллелограмма.

б) Окружность, описанная около треугольника CKD пересекает сторону AD в точке P. Найдите отношение

Загрузка решений доступна для зарегистрировавшихся пользователей

На основаниях AD и BC трапеции ABCD построены квадраты ADMN и BCRS, расположенные вне трапеции. Диагонали трапеции пересекаются в точке T.

а) Докажите, что центры квадратов и точка T лежат на одной прямой.

б) Найдите длину отрезка RN, если а

Загрузка решений доступна для зарегистрировавшихся пользователей

В параллелограмме ABCD проведена диагональ АС. Точка О является центром окружности, вписанной в треугольник ABC. Расстояния от точки О до точки А и прямых AD и AC равны соответственно 10, 8 и 6.

а) Докажите, что ABCD — прямоугольник.

б) Найдите площадь параллелограмма ABCD.

Загрузка решений доступна для зарегистрировавшихся пользователей

Дана трапеция ABCD с основаниями сторона Продолжения боковых сторон пересекаются в точке K, образуя прямой угол AKD. Окружность ω проходит через точки А и В и касается стороны CD в точке P.

а) Найдите площадь трапеции.

б) Найдите радиус окружности ω.

Загрузка решений доступна для зарегистрировавшихся пользователей

В треугольнике ABC провели высоту CC₁ и медиану AA₁. Оказалось, что точки A, A₁, C, C₁ лежат на одной окружности.

а) Докажите, что треугольник ABC равнобедренный.

Загрузка решений доступна для зарегистрировавшихся пользователей

а) Докажите, что четырёхугольник ADA₁B₁ — параллелограмм.

б) Найдите CD, если отрезки AD и ВС перпендикулярны, АС = 63, ВС = 25.

Загрузка решений доступна для зарегистрировавшихся пользователей

В остроугольном треугольнике ABC провели высоту CC₁ и медиану AA₁. Оказалось, что точки A, A₁, C, C₁ лежат на одной окружности.

а) Докажите, что треугольник ABC равнобедренный.

Загрузка решений доступна для зарегистрировавшихся пользователей

На стороне CD трапеции ABCD отмечена точка M, которая является серединой этой стороны.

а) Докажите, что

б) На стороне CD отмечена точка K, такая, что причем AD = 2BC. Расстояние от точки D до прямой AB равно 10. Найдите расстояние от точки K до стороны AB.

Загрузка решений доступна для зарегистрировавшихся пользователей

Биссектриса прямого угла прямоугольного треугольника АВС вторично пересекает окружность, описанную около этого треугольника, в точке L. Прямая, проходящая через точку L и середину N гипотенузы АВ, пересекает катет ВС в точке М.

а) Докажите,

б) Найдите площадь треугольника АВС, если AB = 20 и

Загрузка решений доступна для зарегистрировавшихся пользователей

В прямоугольном треугольнике АВС точка M лежит на катете АС, а точка N лежит на продолжении катета ВС за точку С причем СМ = ВС и CN =&nbspAC.

а) Отрезки СH и CF — высоты треугольников АСВ и NCM соответственно. Докажите, что прямые СН и CF перпендикулярны.

б) Прямые ВМ и AN пересекаются в точке L. Найдите LM если ВС = 4, а АС = 8.

Загрузка решений доступна для зарегистрировавшихся пользователей

Точка Е — середина боковой стороны CD трапеции ABCD. На стороне АВ взяли точку К так, что прямые СК и АЕ параллельны. Отрезки ВЕ и СК пересекаются в точке L.

а) Докажите, что EL — медиана треугольника КСЕ.

б) Найдите отношение площади треугольника ВLC к площади четырехугольника AKCD, если площадь трапеции ABCD равна 100, а .

Загрузка решений доступна для зарегистрировавшихся пользователей

На стороне АВ треугольника АВС взята точка Е, а на стороне ВС — точка D так, что АЕ = 2, CD = 1. Прямые AD и СЕ пересекаются в точке О. Известно, что АВ = ВС = 8, АС = 6.

а) Докажите, что АО : АD = 8 : 11.

б) Найдите площадь четырехугольника BDOE.

Загрузка решений доступна для зарегистрировавшихся пользователей

На стороне АВ выпуклого четырехугольника АВCD выбрана точка М так, что и Утроенный квадрат отношения расстояния от точки А до прямой CD к расстоянию от точки С до прямой AD равен 2, СD = 20.

а) Докажите, что треугольник ACD равнобедренный.

б) Найдите длину радиуса вписанной в треугольник АСD окружности.

Загрузка решений доступна для зарегистрировавшихся пользователей

Отрезки AK, BL, CN — высоты остроугольного треугольника АВС. Точки Р и Q — проекции точки N на стороны АС и ВС соответственно.

а) Докажите, что прямые PQ и KL параллельны.

б) Найдите площадь четырехугольника PQKL, если известно, что CN = 12, AC = 13, BC = 15.

Загрузка решений доступна для зарегистрировавшихся пользователей

В треугольнике ABC на продолжении стороны AC за вершину A отложен отрезок AD, равный стороне AB. Прямая, проходящая через точку A параллельно BD, пересекает сторону BC в точке M.

а) Докажите, что AM — биссектриса угла BAC.

б) Найдите площадь трапеции AMBD, если площадь треугольника ABC равна 216 и известно отношение AC : AB = 5 : 4.

Загрузка решений доступна для зарегистрировавшихся пользователей

Точка A расположена вне квадрата KLMN с центром O, причём треугольник KAN прямоугольный (∠A = 90°) и AK = 2AN. Точка B — середина стороны KN.

а) Докажите, что прямая BM параллельна прямой AN.

б) Прямая AO пересекает сторону ML квадрата в точке P. Найдите отношение LP : PM.

Загрузка решений доступна для зарегистрировавшихся пользователей

Точки E и F расположены соответственно на стороне ВС и высоте ВР остроугольного треугольника АВС так, что AP = 3, BE : EC = 10 : 1, а треугольник AEF является равносторонним.

а) Докажите, что ортогональная проекция точки Е на АС делит отрезок АС в отношении 1 : 16, считая от вершины С.

б) Найдите площадь треугольника AEF.

Загрузка решений доступна для зарегистрировавшихся пользователей

В выпуклом четырехугольнике KLMN точки P и Q — середины сторон NK и LM соответственно. Диагональ КМ делит точкой пересечения отрезок PQ пополам.

а) Докажите, что площадь четырехугольника KLMN в 4 раза больше площади треугольника PMN.

б) Найдите синус угла между диагоналями четырехугольника, вершинами которого служат середины сторон четырехугольника KLMN, если площадь PMN равна KM = 12, NL = 8.

Загрузка решений доступна для зарегистрировавшихся пользователей

В треугольнике ABC биссектрисы AK и BL пересекаются в точке I. Известно, что около четырёхугольника CKIL можно описать окружность.

а) Докажите, что угол BCA равен 60°.

б) Найдите площадь треугольника ABC, если его периметр равен 25 и IC = 4.

Загрузка решений доступна для зарегистрировавшихся пользователей

В четырёхугольнике ABCD противоположные стороны не параллельны. Диагонали четырёхугольника ABCD пересекаются в точке O под прямым углом и образуют четыре подобных треугольника, у каждого из которых одна из вершин — точка O.

а) Докажите, что около четырёхугольника ABCD можно описать окружность.

б) Найдите радиус вписанной окружности, если AC = 10, BD = 26.

Загрузка решений доступна для зарегистрировавшихся пользователей

В четырёхугольнике ABCD противоположные стороны не параллельны. Диагонали четырёхугольника ABCD пересекаются в точке O под прямым углом и образуют четыре подобных треугольника, у каждого из которых одна из вершин — точка O.

а) Докажите, что в четырёхугольник ABCD можно вписать окружность.

б) Найдите радиус вписанной окружности, если AC = 12, BD = 13.

Загрузка решений доступна для зарегистрировавшихся пользователей

На сторонах AC, AB и BC прямоугольного треугольника ABC с прямым углом C вне треугольника ABC построены равнобедренные прямоугольные треугольники AKC, ALB и BMC с прямыми углами K, L и M соответственно.

а) Докажите, что LC — высота треугольника KLM.

б) Найдите площадь треугольника KLM, если LC = 4.

Загрузка решений доступна для зарегистрировавшихся пользователей

На сторонах AC, AB и BC прямоугольного треугольника ABC с прямым углом C вне треугольника ABC построены равнобедренные прямоугольные треугольники AKC, ALB и BMC с прямыми углами K, L и M соответственно.

а) Докажите, что LC — высота треугольника KLM.

б) Найдите площадь треугольника KLM, если LC = 6.

Загрузка решений доступна для зарегистрировавшихся пользователей

Точка M лежит на стороне BC выпуклого четырехугольника ABCD, AB = BM, MC = CD. Биссектрисы углов ABC и BCD пересекаются в точке P, лежащей на стороне AD.

а) Докажите, что четырехугольник ABCD — параллелограмм или трапеция.

б) Найдите площадь четырехугольника ABCD, если известно, что BM : CM = 1 : 3 и площадь четырехугольника, ограниченного прямыми AM, DM, BP и CP, равна 18.

Загрузка решений доступна для зарегистрировавшихся пользователей

В треугольнике ABC проведены две высоты BM и CN, причем AM : CM = 2 : 3 и

а) Докажите, что угол ABC тупой.

б) Найдите отношение площадей треугольников BMN и ABC.

Загрузка решений доступна для зарегистрировавшихся пользователей

Дан параллелограмм ABCD с острым углом A. На продолжении стороны AD за точку D взята точка N

такая, что CN = CD, а на продолжении стороны CD за точку D взята такая точка M, что AD = AM.

а) Докажите, что BM = BN.

б) Найдите MN, если AC = 7,

Загрузка решений доступна для зарегистрировавшихся пользователей

Дан параллелограмм ABCD с острым углом А. На продолжении стороны AD за точку D взята точка M, такая, что CM = СD, а на продолжении стороны CD за точку D взята такая точка N, что AD = AN.

а) Докажите, что BM = BN.

б) Найдите MN, если AC = 4,

Загрузка решений доступна для зарегистрировавшихся пользователей

📹 Видео

Геометрия Диагонали выпуклого четырехугольника ABCD перпендикулярны. Через середины сторон AB и ADСкачать

Четыре точки на окружности | ЕГЭ-2017. Задание 16. Математика. Профильный уровень| Борис ТрушинСкачать

2023 На окружности с центром в точке О отмечены точки А и Б так что угол аоб равен 45Скачать

Вписанный четырёхугольник | ЕГЭ-2018. Задание 16. Математика. Профильный уровень | Борис ТрушинСкачать