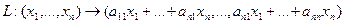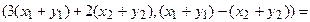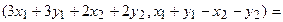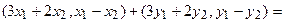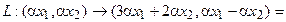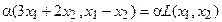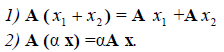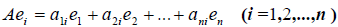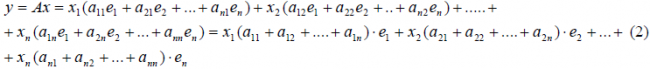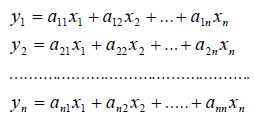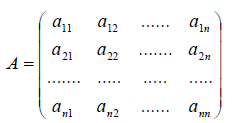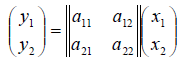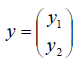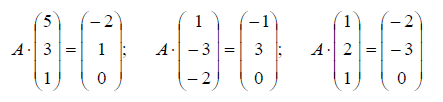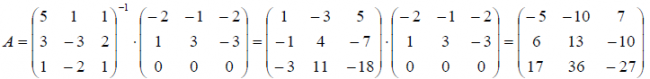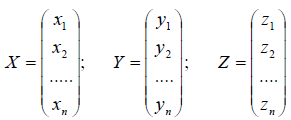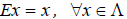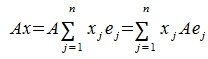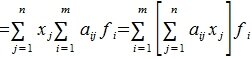Пример №1 . Даны векторы ε1(2;1;3), ε2(3;-2;1), ε3(1;-3;-4), X(7;0;7). Показать, что векторы образуют базис трехмерного пространства и найти координаты вектора X в этом базисе.
Решение. Данная задача состоит из двух частей. Сначала необходимо проверить, образуют ли векторы базис. Векторы образуют базис, если определитель, составленный из координат этих векторов, отличен от нуля, в противном случае вектора не являются базисными и вектор X нельзя разложить по данному базису.
Вычислим определитель матрицы:
| E = |
|
∆ = 2*((-2)*(-4) — (-3)*1) — 3*(1*(-4) — (-3)*3) + 1*(1*1 — (-2)*3) = 14
Определитель матрицы равен ∆ =14
Так как определитель отличен от нуля, то векторы образуют базис, следовательно, вектор X можно разложить по данному базису. Т.е. существуют такие числа α1α2α3, что имеет место равенство:
X = ⓫ε1 + ⓬ε2 + ⓭ε3
Запишем данное равенство в координатной форме:
(7;0;7) = α(2;1;3) + α(3;-2;1) + α(1;-3;-4)
Используя свойства векторов, получим следующее равенство:
(7;0;7) = (2α1;1α1;3α1😉 + (3α2;-2α2;1α2😉 + (1α3;-3α3;-4α3😉
(7;0;7) = (2α1 + 3α2 + 1α3;1α1 -2α2 -3α3;3α1 + 1α2 -4α3)
По свойству равенства векторов имеем:
2α1 + 3α2 + 1α3 = 7
1α1 -2α2 -3α3 = 0
3α1 + 1α2 -4α3 = 7
Решаем полученную систему уравнений методом Гаусса или методом Крамера.
Ответ:
| X = |
|
X = 2ε1 + ε2
В системе векторов a1, a2, a3, a4 найти любую подсистему векторов, которые образуют базис, разложить векторы по базису, перейти к другому базису, найти коэффициенты разложения векторов во втором базисе; в обоих случаях определить обратные матрицы, соответствующие векторам базиса. Правильность вычисления в каждом случае проверить с помощью умножения вектора слева на матрицу, обратную матрице вектора базиса.
Пример №2 . В системе векторов a1, a2, a3, a4 найти любую подсистему векторов, которые образуют базис, разложить векторы по базису, перейти к другому базису, найти коэффициенты разложения векторов во втором базисе; в обоих случаях определить обратные матрицы, соответствующие векторам базиса. Правильность вычисления в каждом случае проверить с помощью умножения вектора слева на матрицу, обратную матрице вектора базиса.
a1=(1;5;3), a2=(2;1;-1), a3=(4;2;1), a4=(17;13;4).
- 5.1.6. Примеры решения задач по теме «Линейные операторы и квадратичные формы»
- Матрица линейного оператора примеры
- Построение матрицы по заданной формуле отображения.
- Матрица линейного оператора
- Примеры линейных операторов
- Действия над операторами
- 1. Понятие линейного оператора
- 2. Сложение линейных операторов
- 3. Умножение линейных операторов
- 4. Умножение линейного оператора на число
- 5. Нулевой оператор
- 6. Противоположный оператор
- 7. Ядро линейного оператора
- 8. Образ линейного оператора
- 9. Ранг линейного оператора
- 📹 Видео
Видео:Собственные векторы и собственные значения матрицыСкачать

5.1.6. Примеры решения задач по теме «Линейные операторы и квадратичные формы»
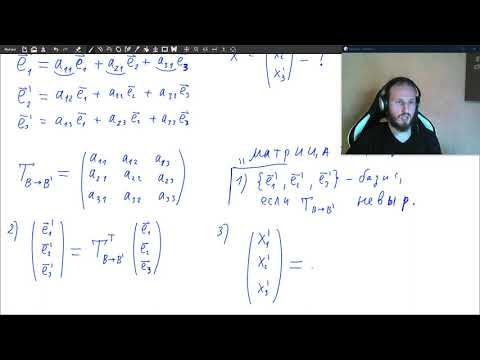
Пусть Е1, Е2, Е3, Е4 – базис в векторном пространстве. Разложить вектор
Выпишите матрицу перехода от старого базиса к новому, столбцами которой являются координаты новых базисных векторов в старом базисе. Строки этой матрицы являются коэффициентами в формулах преобразования старых координат через новые.
Выпишем матрицу перехода от старого базиса к новому, столбцами которой являются координаты новых базисных векторов в старом базисе:

Строки этой матрицы являются коэффициентами в формулах преобразования старых координат через новые.
Координаты вектора Х в старом базисе: Х = (1; 2; -1; 3). Пусть в новом базисе он имеет координаты: X = (X, Y, Z, T). Тогда, используя матрицу Т, найдем связь между старыми и новыми координатами:

Следовательно, в новом базисе Х = (-1; 3; -4; 3).
Найти матрицу А’ оператора А:
Искомая матрица А’ = T-1 A T, где Т – матрица перехода из старого базиса к новому.
Искомая матрица А’ = T-1 A T, где Т – матрица перехода из старого базиса к новому. Составим матрицу Т :



Ответ: 
Найти собственные числа и собственные векторы линейного оператора, заданного матрицей

Для определения собственных чисел составьте характеристическое уравнение:
Координаты собственных векторов RI = (Xi, Yi) должны удовлетворять системе уравнений, коэффициенты которых получены из элементов строк определителя, стоящего в левой части характеристического уравнения, при подстановке LI.
Составим характеристическое уравнение:
Найдем собственные векторы:
1) для L = -2 координаты собственного вектора R1 = (X1, Y1) должны удовлетворять системе уравнений, коэффициенты которых получены из элементов строк определителя, стоящего в левой части характеристического уравнения, при подстановке L = -2:
Если Х1 = 1, то У1 = -1, и R1= (1; -1). Остальные собственные векторы коллинеарны вектору (1; -1), и общий вид собственного вектора, соответствующего L = -2: R1 = С1(1; -1), где С1 – произвольная постоянная.
2) для L = 6 координаты собственного вектора R2 (X2; Y2) удовлетворяют системе:
Пусть Х2 = 3, тогда У2 = 5, и R2 = (3; 5). Соответственно общий вид второго собственного вектора: R2 = С2(3; 5).
Ответ: собственные числа L1 = -2, L2 = 6; собственные векторы R1 = С1(1; -1),
В пространстве 3-мерных векторов задан оператор
Где I – базисный вектор декартовой системы координат.
Выяснить геометрический смысл этого оператора.
Множитель Xi – скалярное произведение, то есть число, поэтому вектор (Xi)I коллинеарен оси Ох.
Оператор А переводит произвольно направленный вектор Х в вектор
KI, коллинеарный оси Ох, поскольку первый множитель – скалярное произведение, то есть число. Из определения скалярного произведения следует, что
Следовательно, А – оператор проектирования на ось Ох.
Оператор осуществляет проектирование вектора Х на ось Ох;
Привести матрицу А линейного оператора к диагональному виду и найти соответствующий базис, если
Найдите собственные числа и собственные векторы матрицы линейного оператора, задайте базис из линейно независимых собственных векторов R1, R2, R3 , в котором матрица оператора примет диагональный вид, и составьте матрицу перехода к новому базису.
Найдем собственные векторы, соответствующие полученным собственным числам.
Подставим в строки определителя L = 2 и найдем связь между координатами собственного вектора R2 = (X2, Y2, Z2):
Та же зависимость получается для координат третьего собственного вектора R3 = (X3, Y3, Z3). Выберем значения двух координат каждого из этих векторов так, чтобы R2 и R3 были линейно независимы.
Пусть Х2 = 1, У2 = 0, тогда Z2 = -3, и R2 = (1; 0; -3).
Получен базис из линейно независимых собственных векторов R1, R2, R3 , в котором матрица оператора примет диагональный вид.
Составим матрицу перехода к новому базису:
Найдем матрицу, обратную к Т:

Тогда в базисе из собственных векторов матрица оператора
Ответ: в базисе (1; 1; 1), (1; 0; -3), (0; 1; 3) матрица оператора
Линейный оператор А задан в некотором базисе матрицей
Найти собственные числа и собственные векторы оператора А-1 – оператора, обратного к А.
Собственные числа обратного оператора являются обратными к собственным числам данного оператора, а их собственные векторы одинаковы.
Характеристическое уравнение для А:
Найдем матрицу обратного оператора:

Соответствующее характеристическое уравнение:
Составить матрицу квадратичной формы 3Х2 – 10Ху + 8У2 и найти ее собственные числа.
Матрица квадратичной формы А11Х2 + 2А12Ху + А22У2 является
Симметрической (Aij = Aji) и имеет вид:
В нашей задаче А11 = 3, А12 = -5, А22 = 8. Следовательно,
Составим характеристическое уравнение, корнями которого являются собственные числа:
Ответ: матрица квадратичной формы 
Собственные числа
Найти базис, в котором квадратичная форма 2Х2 + 4Ху + 5У2 будет иметь канонический вид, и указать этот вид.
Канонический вид квадратичной формы:
1) во-первых, не содержит произведения Ху;
2) во-вторых, коэффициенты при Х2 и У2 равны собственным числам матрицы квадратичной формы.
Базис, в котором квадратичная форма имеет канонический вид, состоит из нормированных собственных векторов матрицы квадратичной формы.
Матрица квадратичной формы
Собственные числа: L1 = 1, L2 = 6.
Для L1 = 1 координаты вектора R1 = <X1, Y1> определяются уравнением
Х1 + 2У1 = 0, Х1 = -2У1. Если У1 = 1, то Х1 = -2, и R1 = C. Найдем значение С из условия, что вектор R1 нормирован, то есть его длина равна 1:
Итак, базис имеет вид:
И в этом базисе квадратичная форма примет вид: L1Х2 + L2У2, то есть Х2 + 6У2.
Ответ: в базисе 
Указать преобразование координат, приводящее квадратичную форму
8Х2 – 12Ху + 17У2 к каноническому виду.
Матрица преобразования координат имеет вид:
Где R1 = (X1, Y1) и R2 = (X2, Y2) – нормированные собственные векторы.
Найдем базис из нормированных собственных векторов.
Составим матрицу перехода к новому базису, столбцами которой будут координаты новых базисных векторов R1, R2 в старом базисе:
Строки этой матрицы определяют коэффициенты уравнений, выражающих старые координаты через новые:
Где Х, У – координаты в старом базисе, а Х’, Y’ – в новом.
Таким образом, найдено искомое преобразование.
Ответ: 
Привести к каноническому виду квадратичную форму 5Х2 – 12Ху.
Матрица преобразования координат имеет вид:
Где R1 = (X1, Y1) и R2 = (X2, Y2) – нормированные собственные векторы. В новом базисе квадратичная форма имеет канонический вид, причем коэффициенты при Х2 и У2 совпадают с собственными числами матрицы квадратичной формы.
Матрица перехода к базису из собственных векторов:
Подставим найденные выражения в квадратичную форму:
Как и следовало ожидать, в новом базисе квадратичная форма имеет канонический вид, причем коэффициенты при Х2 и У2 совпадают с собственными числами матрицы квадратичной формы.
Найти преобразование координат, приводящее квадратичную форму
X2 + Y2 + 5Z2 – 6Xy + 2Xz – 2Yz к каноническому виду.
Матрица преобразования координат:
Для заданной квадратичной формы
Составим и решим характеристическое уравнение:
(Мы не останавливаемся подробно на способах решения уравнений высших порядков. В данном случае, например, один из корней был найден перебором делителей свободного члена, а затем левая часть разложена на множители.)
Найдем нормированные собственные векторы:
Матрица перехода к новому базису:
Задает преобразование координат:
Заметим, что в новых координатах квадратичная форма примет вид:
Где коэффициенты являются собственными числами, стоящими в той же последовательности, что и соответствующие собственные векторы в матрице Т.
Ответ:
Видео:Координаты в новом базисеСкачать

Матрица линейного оператора примеры
Видео:Базис и матрица перехода. Координаты вектора в разных базисах.Скачать

Построение матрицы по заданной формуле отображения.
Пусть отображение задано с помощью формулы:
то есть для координат произвольного исходного вектора определены координаты его образа. Тогда, рассматривая вместо произвольного вектора x вектор 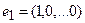
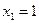
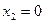
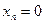
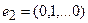
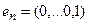
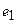
Пример 1. Пусть оператор задан с помощью формулы:
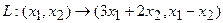
Прежде всего, докажем, что это отображение – действительно линейный оператор.
Отобразим сумму векторов:
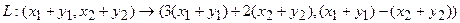
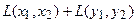
Аналогично для умножения на константу:
Для того чтобы найти матрицу этого линейного оператора, нужно, как было сказано выше, подставить значения x1 = 1, x2 = 0, а затем x1 = 0, x2 = 1. В этом примере образы базисных векторов – соответственно (3, 1) и (2, -1).
Поэтому матрица линейного оператора будет иметь вид:
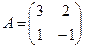
Аналогичным способом решается задача и для 3 и большего количества переменных.
Пример 2. 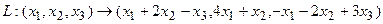
Построим матрицу оператора. Отображая вектор (1,0,0), получаем (1,4,-1), соответственно (0,1,0) переходит в (2,1,-2), а вектор (0,0,1) – в (-1,1,3).
Матрица линейного оператора:
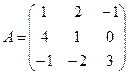
2.2. Построение матрицы оператора в случае, когда известен исходный базис и система векторов, в которую он отображается.
Если задана система 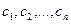
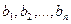
Матрицу этого оператора можно найти двумя способами: с помощью обратной матрицы и с помощью системы уравнений.
Пусть 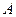
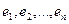
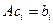
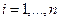
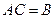
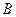
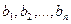
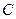
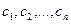
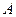
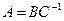
Пример. Найти матрицу линейного оператора, отображающего базис
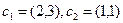
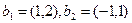
Здесь 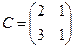
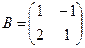
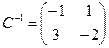
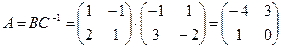
Проверка осуществляется умножением получившейся матрицы на каждый вектор: 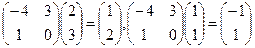
Аналогично решаются подобные задачи и для трёхмерного пространства. В приложении (§5) есть несколько вариантов таких задач.
2.3. Прочие способы нахождения матрицы оператора.
Существуют также примеры, где линейный оператор задаётся другими способами, отличными от рассмотренных в п. 2.1 и 2.2.
Пример. Линейными операторами являются как правое, так и левое векторное умножение на фиксированный вектор в трёхмерном пространстве, то есть отображения вида 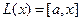
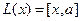
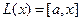
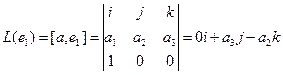
Аналогично, 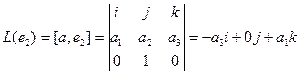
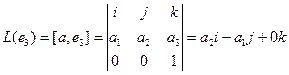
Координаты полученных векторов запишем в виде столбцов матрицы оператора.
Матрица оператора: 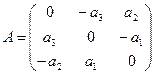
Аналогично можно построить матрицу линейного оператора 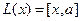
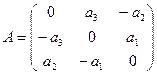
Пример. Линейный оператор дифференцирования в пространстве всех многочленов степени не более n. Это пространство размерности n + 1. Возьмём в качестве базиса элементы 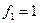
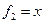
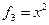
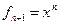
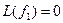
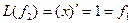
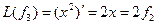
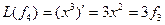
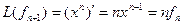
Матрица этого линейного оператора:
Линейные операторы могут отображать не только пространства конечной размерности, но и бесконечномерные пространства. Так, оператор дифференцирования может рассматриваться также в пространстве всех непрерывных функций. (В этом пространстве нет конечного базиса). В этом случае, очевидно, оператор не может быть задан матрицей конечного порядка.
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: Для студента самое главное не сдать экзамен, а вовремя вспомнить про него. 10219 – 

91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно
Видео:Собственные значения и собственные векторы матрицы (4)Скачать

Матрица линейного оператора
Определение 1. Если задан закон, который каждому вектору x?? ставит в соот ветствие вектор y . то говорят, что в линейном пространстве ? задан оператор A , при этом пишут:
Определение 2. Оператор A называется линейным, если для любых x 1 ?? и x 2 ?? и произвольного числа ? выполняются условия:
Рассмотрим теперь в евклидовом пространстве E n базис e 1 ,e 2 . e n и пусть в этом пространстве определён линейный оператор A : y = A x .
Разложим векторы x и y по базису e 1 ,e 2 . e n :
В силу линейности оператора A можно написать
Заметим, что каждый вектор 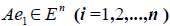
В силу единственности разложения по данному базису мы можем при равнять коэффициенты при базисных векторах в правых частях формул (1) и (2); тогда получим:
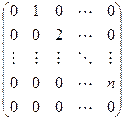
Получили, что линейному оператору A в данном базисе соответствует квадратная матрица
которая называется матрицей линейного оператора A , i -й столбец которой состоит из координат вектора Ae i (i = 1,2. n ) относительно данного базиса. Отметим, что матрица A оператора A зависит от выбора базиса e 1 ,e 2 . e n .
Итак, мы показали, что всякому линейному оператору A в евклидовом пространстве E n соответствует матрица A ; можно доказать и обратное утверждение: всякую квадратную матрицу A можно рассматривать как матрицу некоторого линейного оператора A в данном базисе e 1 ,e 2 . e n .
Представляют интерес невырожденные линейные операторы, т.е. такие операторы, матрицы которых имеют обратную A -1 , т.е. также являются невырожденными. В этом случае каждому вектору y (образу), определённому соотношением, отвечает единственный вектор x (прообраз) и при этом имеет место матричное равенство: X = A -1 ? Y .
Видео:Доказать, что векторы a, b, c образуют базис и найти координаты вектора d в этом базисеСкачать

Примеры линейных операторов
1. В пространстве 2-мерных векторов линейным оператором является правило
связывающее вектор-прообраз 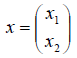
2. В пространстве бесконечно дифференцируемых функций линейным оператором является операция дифференцирования, ставящая в соответствие каждому элементу этого простран ства его производную функцию.
3. В пространстве многочленов P n (t) линейным оператором является операция умножения многочлена на независимую переменную t .
Пример: Известны образы базисных векторов E 3 под действием оператора A :
Найти матрицу этого оператора в исходном базисе.
Решение: По определению y = A x, значит в матричном виде можно записать, что A = X -1 Y . Для нашего примера получаем
Видео:Как разложить вектор по базису - bezbotvyСкачать

Действия над операторами
Сложение линейных операторов. Пусть x?E n , A и B – два линейных оператора в этом пространстве.
Определение 1. Суммой линейных операторов A и B в E n называется оператор C, определяемый равенством Cx = A x + Bx , где x – любой вектор из E n .
Сумма линейных операторов является линейным оператором, причём его матрица C = A + B, где A и B – матрицы линейных операторов A и B .
Умножение линейного оператора на число. Пусть x?E n , линейный оператор A определён в E n , ? – некоторое число.
Определение 2. Произведением линейного оператора A на число ? называется оператор ?A , определяемый равенством 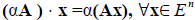
?A является линейным оператором, а матрица этого линейного оператора получается из матрицы A умножением её на число ? , т.е. она равна ? ? A.
Умножение линейных операторов. Пусть x? E n , y ? E n , z ? E n и кроме того в E n определены линейные операторы A и B таким образом, что y = Bx, z = A y .
Определение 3. Произведением A ? B линейных операторов A и B называется оператор C, определяемый соотношением Cx = A (Bx) .
Таким образом, перемножение линейных операторов состоит в последовательном их применении по отношению к вектору x .
Рассмотрим матрицы – столбцы:
и обозначим через A, B и C – соответственно матрицы линейных операторов A, B и C. Тогда Z = A ? (B ? X) = (A ? B) ? X = C ? X , таким образом, C = A ? B, т.е. матрица произведения линей ных операторов также является линейным оператором.
a) (A ? B)(x + y) = A (B(x + y)) = A (Bx + By) = A (Bx) + A (By) = = (A ? B) ? x + (A ? B) ? y
б) (A ? B)(? x) = A (B(? x)) = A (?Bx) =?A (Bx) =? (A ? B)x
Свойства умножения линейных операторов вытекают из свойств умножения матриц.
Определение 4. Линейные операторы A и В называются равными, если 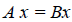
Определение 5. Оператор E называется единичным (или тождественным) оператором, если каждому элементу x линейного пространства 
Видео:Матрица переходаСкачать
1. Понятие линейного оператора
Пусть R и S линейные пространства, которые имеют размерность n и m соответственно. Оператором A действующим из R в S называется отображение вида 
Определение 1. Оператор A действующий из R в S называется линейным, если для любых элементов x1 и x2 пространства R и любого λ из числового поля K выполняются соотношения
Если пространство S совпадает с пространством R, то линейный оператор, который действует из R в R называют линейным преобразованием пространства R.
Пусть заданы два векторных пространства n-мерный R и m-мерный S, и пусть в этих пространствах заданы базисы 

| y=Ax, | (1) |
где A – m×n -матрица с коэффициентами из поля K. Тогда каждому элементу из R соответствует элемент y=Ax из S. Отображение (1) определяет оператор A. Покажем, что этот оператор обладает свойством линейности. Действительно, учитывая свойства умножения матриц, можно записать:
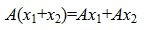 , , | (2) |
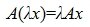 . . |
Покажем теперь обратное, т.е. что для любого линейного оператора A, отображающего пространство R в S и произвольных базисов 

Пусть x − произвольный элемент в R. Тогда
 | (3) |
является разложением x в по базису 
Применим оператор A к базисным векторам 
 | (4) |
где aij − координаты полученного вектора в базисе 
Тогда применяя оператор A к элементу x и учитывая (3) и (4), имеем
Сделаем следующее обозначение:
 | (6) |
Тогда равенство (5) примет следующий вид:
 | (7) |
Из равенства (7) следует, что любой элемент из пространства R при отображении оператором A, в пространстве S и в базисе 
Построим матрицу A с элементами aij:
 | (8) |
Тогда выражение (6) можно записать в матричном виде:
| y=Ax. | (9) |
Матрица A называется матрицей линейного оператора в заданных базисах 

Видео:Матрицы и векторыСкачать

2. Сложение линейных операторов
Пусть A и B два линейных оператора действующих из R в S и пусть A и B – mxn − матрицы соответствующие этим операторам.
Определение 2. Суммой линейных операторов A и B называется оператор C, определяемый равенством
| Cx= Ax+ Bx, x∈R, | (10) |
где x∈R означает, что x принадлежит пространстве R.
Сумма линейных операторов обозначается так C=A+B. Легко убедится, что сумма линейных операторов также является линейным оператором.
Применим оператор C к базисному вектору ej, тогда:
| Cej= Aej+ Bej= | n | (aij+bij) ej |
| ∑ | ||
| j= 1 |
Следовательно оператору C отвечает матрица 
| C=A+B. | (11) |
Видео:Координаты вектора. 9 класс.Скачать

3. Умножение линейных операторов
Пусть заданы три линейных пространства R, S и T. Пусть линейный оператор B отображает R в S, а линейный оператор A отображает S в T.
Определение 3. Произведением операторов A и B называется оператор C, для которого выполняется следующее равенство при любом x из R:
| Cx= A( Bx), x ∈ R. | (12) |
Произведение линейных операторов обозначается C=AB. Легко убедится, что произведение линейных операторов также является линейным оператором.
Таким образом оператор C отображает пространство R в T. Выберем в пространствах R, S и T базисы и обозначим через A, B и C матрицы операторов A, B и C соответствующие этим базисам. Тогда отображения линейных операторов A, B, C
| y=Bx, z=Ay, z=Cx |
можно записать в виде матричных равенств
| y=Bx, z=Ay, z=Cx |
где x, y, z − векторы x, y, z − представленные в виде координатных столбцов. Тогда
| Cx=A(Bx)=(AB)x. |
Учитывая произвольность х, получим
| C=AB. | (13) |
Следовательно произведению операторов C=AB соответствует матричное произведение C=AB.
Видео:Координаты точки и координаты вектора 1.Скачать

4. Умножение линейного оператора на число
Пусть задан линейный оператор A отображающий R в S и некоторое число λ из поля K.
Определение 4. Произведением оператора A на число λ называется оператор C, для которого выполняется следующее равенство при любом x из R:
| Cx=λ ( Ax) | (14) |
Таким образом оператор C отображает пространство R в S. Выберем в пространствах R и S базисы и обозначим через A матрицу оператора A соответствующее этим базисам векторные равенства
| y=Ax, z=λy, z=Cx |
можно записать в виде матричных равенств
| y=Ax, z=λy, z=Cx |
где x, y, z − векторы x, y, z − представленные в виде координатных столбцов. Тогда
| Cx=λ(Ax)=(λA)x. |
Учитывая произвольность х, получим
| C=λA. | (15) |
Следовательно произведению оператора C на число λ соответствует произведение матрицы A на число λ.
Видео:5 4 Координаты Преобразование координат при замене базисаСкачать

5. Нулевой оператор
Оператор, отображающий все элементы пространства R в нулевой элемент пространства S называется нулевым оператором и обозначается через O. Действие нулевого оператора можно записать так:
Видео:Найдите разложение вектора по векторам (базису)Скачать

6. Противоположный оператор
Противоположным оператору A называется оператор −A удовлетворяющий равенству:
Видео:А.7.35 Собственные вектора и собственные значения матрицыСкачать

7. Ядро линейного оператора
Определение 5. Ядром линейного оператора A называется множество всех тех элементов x пространства R, для которых выполняется следующее равенство: Ax=0.
Ядро линейного оператора также называют дефектом оператора. Ядро линейного оператора обозначается символом ker A.
Видео:Линейная алгебра. Векторы и операции над векторами.Скачать

8. Образ линейного оператора
Определение 6. Образом линейного оператора A называется множество всех элементов y пространства R, для которых выполняется следующее равенство: y=Ax для всех x из R.
Образ линейного оператора обозначается символом im A.
Видео:Как найти координаты вектора?Скачать

9. Ранг линейного оператора
Определение 7. Рангом линейного оператора A обозначаемое символом rang A называется число равное размерности образа im A оператора A, т.е.: rang A=dim(im A).
📹 Видео
Замена базиса. ТемаСкачать

Координаты вектора в пространстве. 11 класс.Скачать

Нахождение координат вектора. Практическая часть. 9 класс.Скачать

Базис линейного пространства. Матрица переходаСкачать