На сторонах выпуклого четырехугольника как на диаметрах

Условие

Четыре окружности, построенные как на диаметрах на сторонах выпуклого четырёхугольника ABCD, имеют общую точку, лежащую внутри четырёхугольника.

а) Докажите, что диагонали четырёхугольника ABCD перпендикулярны.

б) Найдите площадь четырёхугольника ABCD, если длина диагонали АС равна sqrt(2), а отрезки, соединяющие середины противоположных сторон, перпендикулярны. [16п4]

Видео:№368. Найдите углы выпуклого четырехугольника, если они равны друг другу.Скачать

Четыре окружности, построенные как на диаметрах на сторонах выпуклого четырехугольника ABCD, имеют общую точку, лежащую внутри четырехугольника, а отрезки, соединяющие середины противоположных сторон ?

Математика | 10 — 11 классы

Четыре окружности, построенные как на диаметрах на сторонах выпуклого четырехугольника ABCD, имеют общую точку, лежащую внутри четырехугольника, а отрезки, соединяющие середины противоположных сторон четырехугольника, взаимно перпендикулярны.

Найдите площадь четырехугольника ABCD, если длина диагонали AC = √2 см.

Так как четырёхугольник выпуклый сAB = AD, BC = CD, то четырёхугольник правильный, следовательно симметричный.

Значит периметры пятиугольников ABCOD и ABOCD одиннаковы

точно не знаю, правильно ли, если чтото не понятно то пиши пожалуйста.

Видео:ОГЭ Задание 24 Площадь выпуклого четырехугольника с перпендикулярными диагоналямиСкачать

Найдите сторону AD четырехугольника ABCD, если AB = 3, BC = 4, CD = 5 и известно, что в четырехугольник ABCD можно вписать окружность?

Найдите сторону AD четырехугольника ABCD, если AB = 3, BC = 4, CD = 5 и известно, что в четырехугольник ABCD можно вписать окружность.

Видео:№369. Найдите углы A, B и C выпуклого четырехугольника ABCD, еслиСкачать

В окружность с центром О вписан четырехугольник со взаимно перпендикулярными диагоналями?

В окружность с центром О вписан четырехугольник со взаимно перпендикулярными диагоналями.

Докажите, что расстояние от точки О до каждой его стороны равно половине длины противоположной стороны.

Видео:Геометрия Диагонали выпуклого четырехугольника ABCD перпендикулярны. Через середины сторон AB и ADСкачать

В четырехугольнике ABCD проведите диагональ AC ; отрезок, соединяющий середины сторон AB и ВС?

В четырехугольнике ABCD проведите диагональ AC ; отрезок, соединяющий середины сторон AB и ВС.

Видео:№370. Найдите углы выпуклого четырехугольника, если они пропорциональны числам 1, 2, 4, 5.Скачать

Около четырехугольника ABCD описана окружность с центром в точке О?

Около четырехугольника ABCD описана окружность с центром в точке О.

Диагонали четырехугольника перпендикулярны.

Найдите длину стороны BC, если расстояние от точки О до стороны AD равно 1.

Видео:#математика #огэ #впр На сторонах угла BAC, равного 20°, и на его биссектрисе отложеныСкачать

Диагонали выпуклого четырехугольника равны m и n?

Диагонали выпуклого четырехугольника равны m и n.

Отрезки, соединяющие середины противолежащих сторон, равны друг другу.

Докажите, что его площадь равна 0, 5mn.

Видео:8 класс, 3 урок, ЧетырехугольникСкачать

Диагонали выпуклого четырехугольника равны m и n?

Диагонали выпуклого четырехугольника равны m и n.

Отрезки, соединяющие середины противолежащих сторон, равны друг другу.

Докажите, что его площадь равна 0, 5mn.

Видео:9 класс. Геометрия. ОГЭ. Окружность. Четырехугольники.Скачать

Известно что около четырехугольника ABCD можно описать окружность и что продолжения сторон AD и BC четырехугольника пересекаются в точке K Докажите что четырехугольник КАВ и КСD подобны?

Известно что около четырехугольника ABCD можно описать окружность и что продолжения сторон AD и BC четырехугольника пересекаются в точке K Докажите что четырехугольник КАВ и КСD подобны.

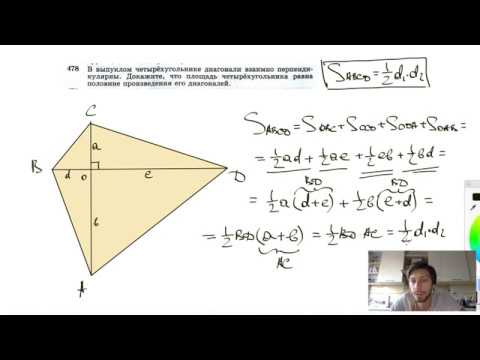
Видео:№478. В выпуклом четырехугольнике диагонали взаимно перпендикулярны. Докажите, что площадьСкачать

Помогите пожалуйста с математикой Стороны четырехугольника AB, BC, CD, DA относятся как 1 : 2 : 3 : 2 соответственно?

Помогите пожалуйста с математикой Стороны четырехугольника AB, BC, CD, DA относятся как 1 : 2 : 3 : 2 соответственно.

Внутри четырехугольника ABCD взята точка Q, равноудаленная от сторон AB, BC и CD.

Определите стороны четырехугольника ABCD, если DQ = 4 см, a угол AQD 90 .

Можно ли описать окружность около четырехугольника ABCD?

Если да, то найдите радиус этой окружности.

Видео:ОГЭ Задание 24 Площадь выпуклого четырехугольникаСкачать

Найдите площадь четырехугольника ABCD?

Найдите площадь четырехугольника ABCD.

Видео:Геометрия Середина M стороны AD выпуклого четырёхугольника равноудалена от всех его вершинСкачать

Диагонали четырехугольника abcd вписанного в окружность перпендикулярны, угол acb = 10°, bdc = 70°?

Диагонали четырехугольника abcd вписанного в окружность перпендикулярны, угол acb = 10°, bdc = 70°.

Найти углы четырехугольника.

Вы открыли страницу вопроса Четыре окружности, построенные как на диаметрах на сторонах выпуклого четырехугольника ABCD, имеют общую точку, лежащую внутри четырехугольника, а отрезки, соединяющие середины противоположных сторон ?. Он относится к категории Математика. Уровень сложности вопроса – для учащихся 10 — 11 классов. Удобный и простой интерфейс сайта поможет найти максимально исчерпывающие ответы по интересующей теме. Чтобы получить наиболее развернутый ответ, можно просмотреть другие, похожие вопросы в категории Математика, воспользовавшись поисковой системой, или ознакомиться с ответами других пользователей. Для расширения границ поиска создайте новый вопрос, используя ключевые слова. Введите его в строку, нажав кнопку вверху.

1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24 = 39 цифр Ответ : в тетради 24 страницы.

Даже простые крестиане могут иметь большой талант , вне зависимости от положения в обществе .

4x + 2>3x + 1 Меняем местами 3х и 2 Получается 4х — 3х> — 2 + 1 (Знаки меняются из за переноса на противоположные) х> — 1.

10 — 6 = 4 96 — 6 = 90 7 — 6 = 1 100 — 6 = 94 216 — 6 = 210 12 — 6 = 6.

1) 216÷3 = 72 (кг) — вторая бригада 2) 216 + 72 = 288(кг) — первая и вторая бригада 3) 288 — 108 = 180(кг) Ответ. 180 кг.

216 + 216 / 3 + (216 + 216 / 3 — 108) = 216 + 72 + 180 = 468.

(х — 18) + (х — 8) + (х — 3) = 23× — 29 = 23 (29 — сумма 18, 8, 3)× = 29 + 23х = 521)52 : 2 = 26 половина2)26 — 18 = 8 страниц в первый день3)26 — 8 = 18 во воторой день4)26 — 3 = 23 в третий день.

Икс поделить на 39 равно 48 икс равен 39 умножить на 48 икс равен 1872 1872 поделить на 39 равно 48.

X : 39 = 48 x = 48×39 x = 1872.

Подели так : отрежь кусок меньше середины (если яблоко 6 см отрежь 2 см) потом столько же (2 см) и всё.

Видео:Что такое выпуклый четырёхугольник? | Математика 8 класс | Геометрия 8 класс | МегаШколаСкачать

На сторонах выпуклого четырехугольника как на диаметрах

БАЗА ЗАДАНИЙ

Задание № 16. Планиметрия с доказательством.

1. Прямая, проходящая через вершину B прямоугольника ABCD перпендикулярно диагонали AC, пересекает сторону AD в точке M, равноудалённой от вершин B и D.
а) Докажите, что ∠ABM =∠DBС = 30°.
б) Найдите расстояние от центра прямоугольника до прямой CM, если BC = 9.

2. К окружности, вписанной в квадрат ABCD, проведена касательная, пересекающая стороны AB и AD в точках M и N соответственно.
а) Докажите, что периметр треугольника AMN равен стороне квадрата.
б) Прямая MN пересекает прямую CD в точке P. В каком отношении делит сторону BC прямая, проходящая через точку P и центр окружности, если AM : MB = 1 : 3?
Ответ: б) 1:3

3. Диагонали AC и BD четырёхугольника ABCD, вписанного в окружность, пересекаются в точке P, причём BC=CD.
а) Докажите, что AB:BC = AP:PD.
б) Найдите площадь треугольника COD, где O— центр окружности, вписанной в треугольник ABD, если дополнительно известно, что BD — диаметр описанной около четырёхугольника ABCD окружности, AB = 6, а BC = 6√2.
Ответ: б) 18√3

4. В треугольнике ABC точки A ₁ , B ₁ , C ₁ — середины сторон BC, AC и A B соответственно, AH— высота, ∠BAC = 60°, ∠BCA = 45°.
а) Докажите, что точки A₁, B₁, C₁, H— лежат на одной окружности.
б) Найдите A₁ H, если BC = 2√3.

5. Две окружности касаются внутренним образом в точке A, причём меньшая проходит через центр большей. Хорда BC большей окружности касается меньшей в точке P. Хорды AB и AC пересекают меньшую окружность в точках K и M соответственно.
а) Докажите, что прямые KM и BC параллельны.
б) Пусть L— точка пересечения отрезков KM и AP. Найдите AL, если радиус большей окружности равен 10, а BC = 16.
Ответ: б) √10

6. Две окружности касаются внутренним образом в точке A, причём меньшая окружность проходит через центр O большей. Диаметр BC большей окружности вторично пересекает меньшую окружность в точке M, отличной от A. Лучи AO и AM вторично пересекают большую окружность в точках P и Q соответственно. Точка C лежит на дуге AQ большей окружности, не содержащей точку P.
а) Докажите, что прямые PQ и BC параллельны.
б) Известно, что sin ∠AOC=√15/4. Прямые PC и AQ пересекаются в точке K. Найдите отношение QK:KA.
Ответ: б) 1:4

7. Две окружности касаются внутренним образом в точке K, причём меньшая проходит через центр большей. Хорда MN большей окружности касается меньшей в точке C. Хорды KM и KN пересекают меньшую окружность в точках A и B соответственно, а отрезки KC и AB пересекаются в точке L.
а) Докажите, что CN:CM = LB:LA.
б) Найдите MN, если LB:LA = 2:3, а радиус малой окружности равен √23.
Ответ: б) 115/6

8. Дан прямоугольный треугольник ABC с прямым углом C. На катете AC взята точка M. Окружность с центром O и диаметром CM касается гипотенузы в точке N.
а) Докажите, что прямые MN и BO параллельны.
б) Найдите площадь четырёхугольника BOMN, если CN = 4 и AM:MC = 1:3.

9. Точка B лежит на отрезке AC. Прямая, проходящая через точку A, касается окружности с диаметром BC в точке M и второй раз пересекает окружность с диаметром AB в точке K. Продолжение отрезка MB пересекает окружность с диаметром AB в точке D.
а) Докажите, что прямые AD и MC параллельны.
б) Найдите площадь треугольника DBC, если AK = 3 и MK = 12.

10. Точка M лежит на стороне BC выпуклого четырёхугольника ABCD, причём B и C — вершины равнобедренных треугольников с основаниями AM и DM соответственно, а прямые AM и MD перпендикулярны.
а) Докажите, что биссектрисы углов при вершинах B и C четырёхугольника ABCD пересекаются на стороне AD.
б) Пусть N— точка пересечения этих биссектрис. Найдите площадь четырёхугольника ABCD, если известно, что BM:MC=1:3, а площадь четырёхугольника, стороны которого лежат на прямых AM, DM, BN и CN, равна 18.

11. В равнобедренном тупоугольном треугольнике ABC на продолжение боковой стороны BC опущена высота AH. Из точки H на сторону AB и основание AC опущены перпендикуляры HK и HM соответственно.
а) Докажите, что отрезки AM и MK равны.
б) Найдите MK, если AB = 5, AC = 8.
Ответ: б) 2,88

12. Точка O — центр окружности, описанной около остроугольного треугольника ABC, I — центр вписанной в него окружности, H — точка пересечения высот. Известно, что ∠BAC = ∠OBC+∠OCB.
а) Докажите, что точка H лежит на окружности, описанной около треугольника BOC.
б) Найдите угол OHI, если ∠ABC = 55°.

13. Точки P, Q, W делят стороны выпуклого четырёхугольника ABCD в отношении AP:PB = CQ:QB = CW:WD = 3:4, радиус окружности, описанной около треугольника PQW, равен 10, PQ = 16, QW = 12, угол PWQ— острый.
а) Докажите, что треугольник PQW— прямоугольный.
б) Найдите площадь четырёхугольника ABCD.

14. Окружность проходит через вершины В и С треугольника АВС и пересекает АВ и АС в точках C ₁ , B ₁ соответственно.
а) Докажите, что треугольник АВC подобен треугольнику AB ₁ C ₁ .
б) Вычислите длину стороны ВС и радиус данной окружности, если ∠ А = 45°, B ₁ C ₁ =6 и площадь треугольника AB ₁ C ₁ в восемь раз меньше площади четырёхугольника BCB ₁ C _{1 .}

15. Дана трапеция ABCD с основаниями AD и BC. Диагональ BD разбивает её на два равнобедренных треугольника с основаниями AD и CD.
а) Докажите, что луч AC— биссектриса угла BAD.
б) Найдите CD, если известны диагонали трапеции: AC = 15 и BD = 8,5.

16. В прямоугольном треугольнике АВС с прямым углом С точки М и N – середины катетов АС и ВС соответственно, СН – высота.
а) Докажите, что прямые MH и NH перпендикулярны
б) Пусть Р – точка пересечения прямых АС и NH, а Q – точка пересечения прямых ВС и MH. Найдите площадь треугольника PQM, если АН = 12 и ВН = 3.

17. В треугольнике АВС угол АВС равен 60°. Окружность, вписанная в треугольник, касается стороны AC в точке M.
а) Докажите, что отрезок BM не больше утроенного радиуса вписанной в треугольник окружности.
б) Найдите sin ∠BMC если известно, что отрезок ВМ в 2,5 раза больше радиуса вписанной в треугольник окружности.
Ответ: б) 0,65

18. В треугольнике АВС проведены высоты АК и СМ. На них из точек М и К опущены перпендикуляры МЕ и КН соответственно.
а) Докажите, что прямые ЕН и АС параллельны.
б) Найдите отношение ЕН:АС, если угол АВС равен 30.
Ответ: б) 3:4

19. Окружность, вписанная в треугольник KLM, касается сторон KL, LM, MK в точках A, B и C соответственно.
а) Докажите, что KC = (KL+KM-LM)/2 .

б) Найдите отношение LB:BM, если известно, что KC:CM = 3:2 и ∠ MKL = 60.
Ответ: б) 5:2

20. Дана равнобедренная трапеция ABCD с основаниями AD и BC. Окружность с центром O, построенная на боковой стороне AB как на диаметре, касается боковой стороны CD и второй раз пересекает большее основание AD в точке H, точка Q — середина CD.
а) Докажите, что четырёхугольник DQOH — параллелограмм.
б) Найдите AD, если ∠BAD = 75° и BC =1.
Ответ: б) 3

21. Квадрат ABCD вписан в окружность. Хорда CE пересекает его диагональ BD в точке K.
а) Докажите, что CK*CE = AB*CD.
б) Найдите отношение CK к KE, если ∠ ECD = 15.
Ответ: б) 2:1

22. В прямоугольном треугольнике ABC точки M и N – середины гипотенузы AB и катета BC соответственно. Биссектриса ∠ BAC пересекает прямую MN в точке L
а) Докажите, что треугольники AML и BLC подобны.
б) Найдите отношение площадей этих треугольников, если cos ∠BAC = 7/25.
Ответ: б) 25:36

23. Окружность касается стороны AC остроугольного треугольника ABC и делит каждую из сторон AB и BC на три равные части.
а) Докажите, что треугольник ABC равнобедренный.
б) Найдите, в каком отношении высота этого треугольника делит сторону BC.
Ответ: б) 5:4

24. На катетах AC и BC прямоугольного треугольника ABC как на диаметрах построены окружности, второй раз пересекающиеся в точке M. Точка Q лежит на меньшей дуге MB окружности с диаметром BC. Прямая CQ второй раз пересекает окружность с диаметром AC в точке P.
а) Докажите, что прямые PM и QM перпендикулярны.
б) Найдите PQ, если AM = 1, BM = 3, а Q – середина дуги MB.

25. Окружность, построенная на медиане BM равнобедренного треугольника ABC как на диаметре, второй раз пересекает основание BC в точке K.
а) Докажите, что отрезок BK втрое больше отрезка CK.
б) Пусть указанная окружность пересекает сторону AB в точке N. Найдите AB, если BK = 24 и BN = 23.

26. В прямоугольной трапеции ABCD с прямым углом при вершине A расположены две окружности. Одна из них касается боковых сторон и большего основания AD, вторая – боковых сторон, меньшего основания BC и первой окружности.
а) Прямая, проходящая через центр окружностей, пересекает основание AD в точке P. Докажите, что AP/PD = sin ∠D.
б) Найдите площадь трапеции, если радиусы окружностей равны 3 и 1.

27. В трапецию ABCD с основаниями AD и BC вписана окружность с центром O.
а) Докажите, что sin ∠AOD = sin ∠ BOS.
б) Найдите площадь трапеции, если ∠ BAD = 90, а основания равны 5 и 7.

28. Дана трапеция с диагоналями равными 8 и 15. Сумма оснований равна 17.
а) Докажите, что диагонали перпендикулярны.
б) Найдите площадь трапеции.

📺 Видео

8 класс, 2 урок, Выпуклый многоугольникСкачать

Геометрия Выпуклый четырехугольник ABCD таков, что угол BAC = углу BDA и угол BAD = углу ADC = 60Скачать

Многоугольники. Математика 8 класс | TutorOnlineСкачать

Задание 24 ОГЭ по математике. Геометрические фигуры. Сумма трех углов выпуклого четырехугольника 300Скачать

Найдите углы четырёхугольникаСкачать

Сумма внутренних углов многоугольника. Выпуклые и невыпуклые многоугольники. 8 класс.Скачать

№378. Докажите, что параллелограмм является выпуклым четырехугольником.Скачать

№367. Найдите стороны четырехугольника, если его периметр равен 66 смСкачать