На сторонах вс и ад выпуклого четырехугольника авсд отмечены точки к и м соответственно

Видео:В треугольнике ABC на сторонах АВ и ВС отмечены точки М и К соответственно, ВМ/АВ = 1/2, ВК/ВС = 4/5Скачать

Ваш ответ

Видео:Геометрия Диагонали выпуклого четырехугольника ABCD перпендикулярны. Через середины сторон AB и ADСкачать

решение вопроса

Видео:№380. На сторонах АВ, ВС, CD и DA четырехугольника ABCD отмечены соответственно точки М, N, Р и QСкачать

Похожие вопросы

• Все категории
• экономические 43,277
• гуманитарные 33,618
• юридические 17,900
• школьный раздел 606,754
• разное 16,824

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.

Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.

Видео:Вариант ФИПИ #5 все задачи (математика ОГЭ)Скачать

На сторонах вс и ад выпуклого четырехугольника авсд отмечены точки к и м соответственно

Вариант 1

1. В четырехугольнике ABCD: АВ || CD, ВС || AD, АС = 20 см, BD = 10 см, АВ = 13 см. Диагонали четырехугольника ABCD пересекаются в точке О. Найдите периметр Δ COD.
2. Из вершины В параллелограмма ABCD с острым углом А проведен перпендикуляр ВК к прямой AD; ВК = АВ : 2. Найдите ∠C, ∠D.
3. Середина отрезка BD является центром окружности с диаметром АС, причем точки А, В, С, D не лежат на одной прямой. Докажите, что ABCD – параллелограмм.

Вариант 2

1. В четырехугольнике ABCD АВ || CD, ВС || AD, О – точка пересечения диагоналей. Периметр Δ AOD равен 25 см, АС = 16 см, BD = 14 см. Найдите ВС.
2. В параллелограмме ABCD с острым углом А из вершины В опущен перпендикуляр ВК к прямой AD, AK = ВК. Найдите ∠C, ∠D.
3. Дан параллелограмм ABCD. На продолжении диагонали АС за вершины А и С отмечены точки М и N соответственно так, что AM = CN. Докажите, что MBND – параллелограмм.

II уровень сложности (задания)

Вариант 3

1. В четырехугольнике ABCD ∠А + ∠B = 180°, АВ || CD. На сторонах ВС и AD отмечены точки М и К соответственно так, что ВМ = KD. Докажите, что точки М и К находятся на одинаковом расстоянии от точки пересечения диагоналей четырехугольника.
2. На сторонах РК и МН параллелограмма МРКН взяты точки А и В, соответственно МР = РВ = АК; ∠MPB = 60°. Найдите углы параллелограмма и сравните отрезки ВМ и АН.
3. На основании АС равнобедренного треугольника АВС отмечена точка К, а на сторонах АВ и ВС – точки М и Р соответственно, причем РК = MB, ∠KPC = 80°, ∠C = 50°. Докажите, что КМВР – параллелограмм.

Вариант 4

1. В четырехугольнике МРКН ∠PMK = ∠HKM, РК || МН. Через точку пересечения диагоналей проведена прямая, пересекающая стороны РК и МН в точках А и В соответственно. Докажите, что АР = НВ.
2. На сторонах ВС и AD параллелограмма ABCD взяты точки М и К, АВ = ВМ = KD, ∠AMB = 30°. Найдите угол параллелограмма и сравните отрезки АМ и СК.
3. В треугольнике МРК ∠M = 65°. На сторонах МК, МР, РК отмечены точки А, В, С соответственно так, что середина стороны РК – точка С, AM = КС, BP = АС, ∠BAM = 50°. Докажите, что ВРСА – параллелограмм.

III уровень сложности (задания)

Вариант 5

1. В выпуклом четырехугольнике ABCD ∠A + ∠B = ∠B + ∠C = = 180°. Через точку О пересечения диагоналей четырехугольника проведена прямая, пересекающая стороны ВС и AD в точках М и К соответственно; ∠BOM = 90°. Докажите, что KD = ВМ.
2. На сторонах ВС и CD параллелограмма ABCD отмечены точки М и Н соответственно так, что отрезки ВН и MD пересекаются в точке О; ∠BHD = 95°, ∠DMC = 90°, ∠BOD = 155°. Найдите отношение длин отрезков АВ и MD и углы параллелограмма.
3. Точки М и К являются соответственно серединами сторон АВ и ВС треугольника АВС. Через вершину С вне треугольника проведена прямая, параллельная АВ и пересекающая луч МК в точке Е. Докажите, что КЕ = АС : 2.

Вариант 6

1. В выпуклом четырехугольнике МРКН ∠M + ∠P = 180°, ∠MKH = ∠KMP. На сторонах МН и РК отмечены точки А и В так, что РВ = РА. Отрезок АВ проходит через точку пересечения диагоналей четырехугольника. Докажите, что HP ⊥ АВ.
2. На сторонах ВС и CD параллелограмма ABCD взяты точки К и М соответственно. Отрезки ВМ и KD пересекаются в точке О; ∠BOD = 140°, ∠DKB = 110°, ∠BMC = 90°. Найдите отношение длин отрезков МС и AD и углы параллелограмма.
3. Точки А и В принадлежат соответственно сторонам РЕ и ЕТ треугольника РЕТ. Прямая, проходящая через вершину Т вне треугольника, пересекает луч АВ в точке К так, что АР = КТ, АВ = ВК= РТ : 2. Докажите, что точка А является серединой отрезка РЕ.

Геометрия 8 Атанасян Самостоятельная 2. ОТВЕТЫ

I уровень сложности (ответы)

Вариант 1

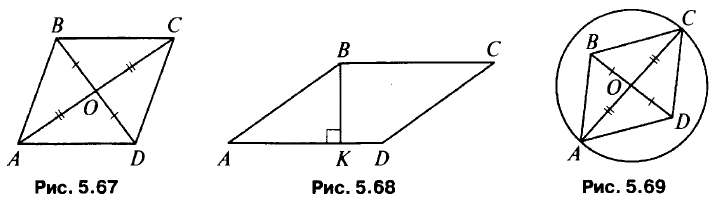
1. ABCD – параллелограмм (рис. 5.67), тогда CD = АВ = 13 см, ОС = АО = 10 см, BD = OD = 5 см (объясните). P_COD = 10 + 5 + 13 = 28 см.
2. ВК = АВ/2 (рис. 5.68), тогда ∠A = 30° (объясните), значит, ∠C = 30°, ∠D = 150° (объясните).
3. В четырехугольнике ABCD (рис. 5.69) середину отрезка BD отметим точкой О. Отсюда следует, что BO = OD.
   Одновременно точка О является центром окружности с диагональю AC, следовательно AO = OC.
   По свойству параллелограммов (диагонали пересекаются и точкой пересечения делятся пополам), если BO = OD и AO = OC, то ABCD – параллелограмм.

Вариант 2

1. ABCD – параллелограмм (рис. 5.70), тогда АО = СО = 8 см, ВО = DO = 7 см (объясните). Так как P_AOD = 25 см, то ВС = AD = 10 см.
2. AK = ВК (рис. 5.71), тогда ∠A = 45° (объясните), ∠C = 45°, ∠D = 135° (объясните).
3. ABCD – параллелограмм (рис. 5.72), тогда АО = СО, ВО = DO. В четырехугольнике MBND диагонали точкой пересечения делятся пополам, значит, MBND – параллелограмм.

II уровень сложности (ответы)

Вариант 1

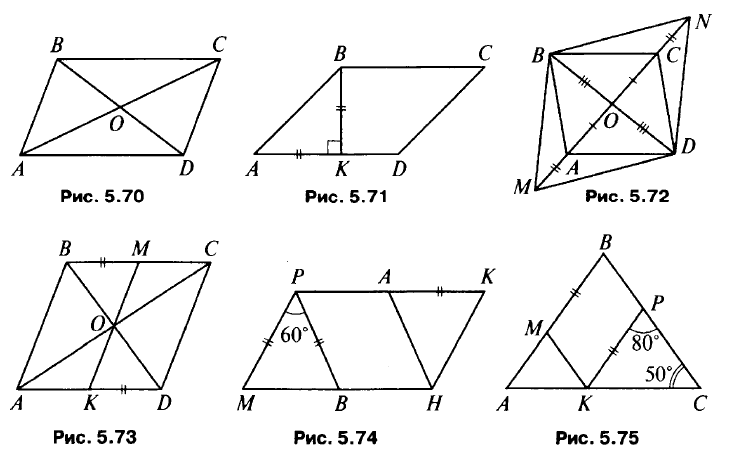
1. (рис. 5.73) а) Докажите, что ABCD – параллелограмм и ВС || AD. б) Докажите, что ΔBOM = ΔDOK и ОМ = ОК.
2. (рис. 5.74) а) Докажите, что ΔМРВ – равносторонний, ∠M = 60°, ∠K = 60. б) Докажите, что ΔАКН – равносторонний, ΔАКН = ΔМРВ, тогда МВ = АН, ∠M = ∠K = 60°, ∠P = ∠H = 120°.
3. (рис. 5.75) а) Найдите ∠B и докажите, что МВ || КР. б) Докажите, что МВРК – параллелограмм.

Вариант 2

1. (рис. 5.76) а) Докажите, что МРКН – параллелограмм и РО = НО. б) Докажите, что ΔРОА = ΔНОВ и РА = НВ.
2. (рис. 5.77) а) Докажите, что ΔАВМ – равнобедренный, ∠B = 120°, ∠BAD = 60°. б) Докажите, что ΔАВМ = ΔKDC и AM = КС, ∠B = ∠D = 120°, ∠14 = ∠C = 60°.
3. (рис. 5.78.) а) Докажите, что в ΔАВМ МА = ВА. б) Докажите, что ВРСА – параллелограмм.

III уровень сложности (ответы)

Вариант 1

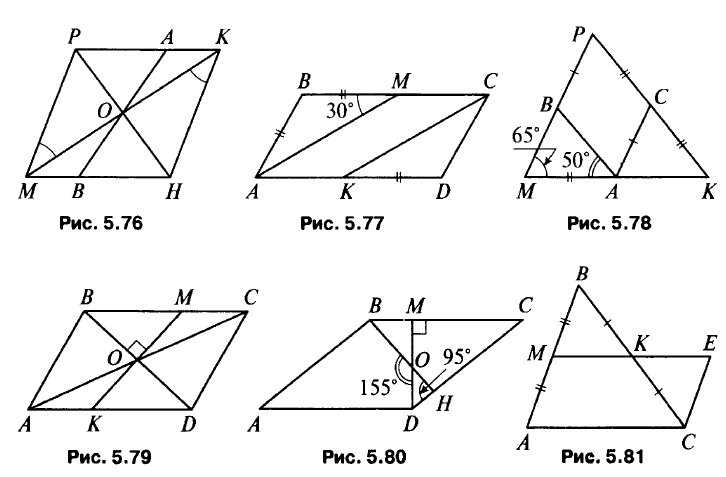
1. (рис. 5.79) а) Докажите, что ΔBCD – параллелограмм и АО = СО. б) Докажите, что ΔАОК = ΔСОМ и КО = МО. в) Докажите, что ΔDKO = ΔВМО и KD = ВМ.
2. (рис. 5.80) ∠MDC = 60°, ∠MCD = 30° (объясните). MD = CD/2, AB : MD = 2 : 1, ∠C = ∠A = 30°, ∠B = ∠D = 150°.
3. (рис. 5.81) а) Докажите, что ΔMВК = ΔЕСК и ЕС = МВ = AM, КЕ = МК = ME/2; б) Докажите, что АМЕС – параллелограмм и ME = АС, т. е. КЕ = АС/2.

Вариант 2

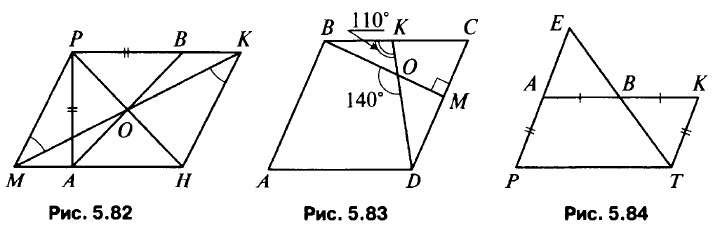
1. (рис. 5.82) а) Докажите, что МРКН – параллелограмм и МО = ОК. б) Докажите, что ΔMОА = ΔКОВ и АО = ОВ. в) Докажите, что РО⊥АВ и PH⊥АВ.
2. (рис. 5.83) ∠KDC = 50°, ∠MCB = 60°, ∠CBM = 30° (объясните). СМ = ВС/2; МС : AD = 1 : 2; ∠C = ∠A = 60°, ∠B = ∠D = 120°.
3. (рис. 5.84) а) Докажите, что РАКТ – параллелограмм и РЕ || КТ. б) Докажите, что ΔАЕВ = ΔКТВ и АЕ = КТ = РА, т. е. А – середина РЕ.

Вы смотрели: Геометрия 8 класс (УМК Атанасян и др. — Просвещение). Урок 4. Самостоятельная работа № 2 «Параллелограмм» с ответами (3 уровня сложности по 2 варианта в каждом). Геометрия 8 Атанасян Самостоятельная 2. Ориентировано на работу с базовым учебником: «Атанасян Л.С., Бутузов В.Ф. и др. Геометрия. 7—9 классы. Учебник для общеобразовательных организаций. М.: Просвещение». В учебных целях использованы цитаты из пособия «Поурочные разработки по геометрии. 7 класс / Гаврилова Н.Ф. — М.: ВАКО».

Видео:Самое сложное задание из досрочного ЕГЭ 2019Скачать

На сторонах вс и ад выпуклого четырехугольника авсд отмечены точки к и м соответственно

Видео:Геометрия Середина M стороны AD выпуклого четырёхугольника равноудалена от всех его вершинСкачать

Источник задания: Решение 2951. ЕГЭ 2016 Математика, И.В. Ященко. 30 вариантов. Ответ.

Задание 16. На сторонах АВ, ВС, CD и AD параллелограмма ABCD отмечены точки K, L, М и N соответственно, причем AK/KB=BL/LC=CM/MD=DN/NA.

а) Докажите, что четырёхугольник KLMN — параллелограмм, а его центр совпадает с центром параллелограмма ABCD.

б) Найдите отношение площадей параллелограммов KLMN и ABCD, если известно, что AK/KB = 2.

а) Так как ABCD – параллелограмм, то , , AB=CD, BC=AD, , . Обозначим через отрезок KB, соответственно, длина отрезка , где — некоторое положительное число. Аналогично определим и для других отрезков (см. рисунок):

Рассмотрим треугольники KBL и MDN, которые равны по двум сторонам и углу (см. рисунок), следовательно, KL=MN. По аналогии из треугольников AKN и CML следует равенство KN=LM. Таким образом, доказали, что KLMN – параллелограмм.

б) Так как , то число . Площадь параллелограмма ABCD можно найти по формуле

.

Площадь параллелограмма KLMN можно найти как разность между площадью параллелограмма ABCD и четырех равных площадей треугольников KBL, LCM, NDM и ANK:

и отношение площадей равно

.

Ответ: .

🌟 Видео

Четырехугольники, вписанные в окружность. 9 класс.Скачать

№555. Точки М, N и Р лежат соответственно на сторонах АВ, ВС и СА треугольника ABC, причем MN||AC,Скачать

18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать

Геометрия На сторонах AD и BC параллелограмма ABCD взяты соответственно точки M и N, причём MСкачать

Геометрия Стороны AB и CD выпуклого четырехугольника ABCD равны. Через середины диагоналей AC и BDСкачать

Геометрия На сторонах AB и BC треугольника ABC отмечены соответственно точки M и K так, что AM = 3BMСкачать

Задание 3 ЕГЭ по математике. Урок 41Скачать

Геометрия Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точкахСкачать

8 класс, 3 урок, ЧетырехугольникСкачать

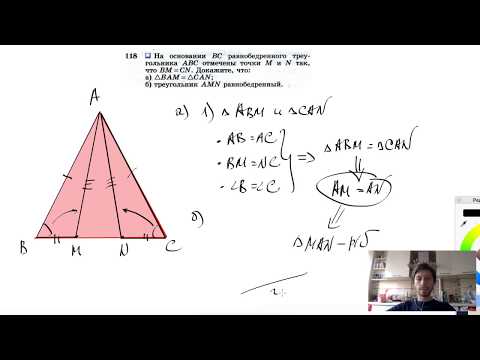
№118. На основании ВС равнобедренного треугольника ABC отмечены точки М и N так, что BM=CN. ДокажитеСкачать

ОГЭ Задание 24 Площадь выпуклого четырехугольника с перпендикулярными диагоналямиСкачать

Вариант ФИПИ #36 все задачи (математика ОГЭ)Скачать

ОПИСАННЫЕ И ВПИСАННЫЕ ОКРУЖНОСТИ ЧЕТЫРЕХУГОЛЬНИКА . §10 геометрия 8 классСкачать

Вариант ФИПИ #5 все задачи (математика ОГЭ)Скачать