Цель: получить уравнение касательной к графику функции.
I. Сообщение темы и цели уроков
II. Повторение и закрепление пройденного материала
1. Ответы на вопросы по домашнему заданию (разбор нерешенных задач).
2. Контроль усвоения материала (тест).
1. Найдите производную функции у = 3х4 – 2 cos x .
Ответ: 
2. Вычислите значение производной функции 
в точке х = π.
Ответ: 
3. Решите уравнение y ’( x ) = 0, если 
Ответ: 
1. Найдите производную функции у = 5хб + 3 sin x .
Ответ: 
2. Вычислите значение производной функции 
в точке х = π.
Ответ: 
3. Решите уравнение y ’(х) = 0, если 
Ответ: 
III. Изучение нового материала
Наконец перейдем к заключительному этапу изучения производной и рассмотрим на оставшихся занятиях применение производной. На этом занятии обсудим касательную к графику функции.
Понятие касательной уже рассматривалось ранее. Было показано, что график дифференцируемой в точке а функции f (х) вблизи а практически не отличается от графика касательной, а значит, он близок к секущей, проходящей через точки (а; f (а)) и (а + Δх; f (а + Δх)). Любая из таких секущих проходит через точку М(а; f (а)). Чтобы написать уравнение касательной, надо задать ее угловой коэффициент. Угловой коэффициент секущей Δ f /Δ x при Δх → 0 стремится к числу f ‘(а), которое является угловым коэффициентом касательной. Поэтому говорят, что касательная есть предельное положение секущей при Δх → 0.
Теперь получим уравнение касательной к графику функции f (х). Так как касательная является прямой и ее угловой коэффициент f ‘(а), то можно записать ее уравнение у = f ‘( a ) · x + b . Найдем коэффициент b из условия, что касательная проходит через точку М(а; f (а)). Подставим координаты этой точки в уравнение касательной и получим: f (а) = f ‘( a ) · a + b , откуда b = f (а) — f ‘(а) · а. Теперь подставим найденное значение b в уравнение касательной и получим: 
или 
Это и есть уравнение касательной. Обсудим применение уравнения касательной.
Под каким углом синусоида 
пересекает ось абсцисс в начале координат?
Угол, под которым график данной функции пересекает ось абсцисс, равен углу наклона а касательной, проведенной к графику функции f ( x ) в этой точке. Найдем производную: 
Учитывая геометрический смысл производной, имеем: 
и a = 60°.
Напишем уравнение касательной графику функции f (х) = -х2 + 4х в точке a = 1.
Найдем производную данной функции: 
Вычислим значения производной f ‘(х) и самой функции f ( x ) в точке a = 1 и получим: f ‘( a ) = f ‘(1) = -2 · 1 + 4 = 2 и f ( a ) = f (1) = -12 + 4 · 1 = 3. Подставим эти величины в уравнение касательной. Имеем: у = 2(х — 1) + 3 или у = 2х + 1.
Для наглядности на рисунке приведены график функции f ( x ) и касательная к этой функции. Касание происходит в точке M (1; 3).
На основе примеров 1 и 2 можно сформулировать алгоритм получения уравнения касательной к графику функции у = f ( x ):
1) обозначить абсциссу точки касания буквой а;
2) вычислить f (а);
3) найти f ‘( x ) и вычислить f ‘( a );
4) подставить найденные числа a , f ( a ), f ‘( a ) в формулу y = f ’( a )( x — a ) + f ( a ).
Заметим, что изначально точка а может быть неизвестна и ее приходится искать из условий задачи. Тогда в алгоритме в п. 2 и 3 слово «вычислить» надо заменить словом «записать» (что иллюстрирует пример 3).
В примере 2 абсцисса а точки касания была задана напрямую. Во многих случаях точка касания определяется различными дополнительными условиями.
Напишем уравнения касательных, проведенных из точки A (0; 4) к графику функции f ( x ) = — x 2 + 2х.
Легко проверить, что точка А не лежит на параболе. Вместе с тем неизвестны точки касания параболы и касательных, поэтому для нахождения этих точек будет использовано дополнительное условие — прохождение касательных через точку А.
Предположим, что касание происходит в точке а. Найдем производную функции: 
Вычислим значения производной f ‘( x ) и самой функции f (х) в точке касания а и получим: f ’(а) = -2а + 2 и f ( a ) = -а2 + 2а. Подставим эти величины в уравнение касательной. Имеем: 
или 
Это уравнение касательной.
Запишем условие прохождения касательной через точку А, подставив координаты этой точки. Получим: 4 
или 4 = а2, откуда а = ±2. Таким образом, касание происходит в двух точках В(-2; -8) и С(2; 0). Поэтому таких касательных будет две. Найдем их уравнения. Подставим значения а = ±2 в уравнение касательной. Получим: при a = 2 
или ух = -2х + 4; при a = -2 
или у2 = 6х + 4. Итак, уравнения касательных у1 = -2х + 4 и у2 = 6х + 4.
Найдем угол между касательными, используя условия предыдущей задачи.
Проведенные касательные у1 = -2х + 4 и у2 = 6х + 4 составляют с положительным направлением оси абсцисс углы а1 и а2 (причем tg a 1 = -2 и tg a 2 = 6) и между собой угол φ = a 1 — а2. Найдем, используя известную формулу, 
откуда φ = arctg 8/11.
Напишем уравнение касательной к графику функции 
параллельной прямой у = -х + 2.
Две прямые параллельны друг другу, если они имеют равные угловые коэффициенты. Угловой коэффициент прямой у = -х + 2 равен -1, угловой коэффициент искомой касательной равен f ’( a ), где a — абсцисса точки касания. Поэтому для определения а имеем дополнительное условие f ’( a ) = -1.
Используя формулу для производной частного функций, найдем производную: 
Найдем значение производной в точке a и получим: 
Получим уравнение 
или (а — 2)2 = 4, или а — 2 = ±2, откуда а = 4 и а = 0. Таким образом, существуют две касательные, удовлетворяющие условию задачи. Подставим значения а = 4 и а = 0 в уравнение касательной у = f ’( a )( x — а) + f (а). При а = 4 имеем: 
и касательная у1 = -(х — 4) + 3 или у1 = -х + 7. При а = 0 получим: 
и касательная у2 = -(х — 0) – 1 или у2 = -х — 1. Итак, уравнения касательных у1 = -х + 7 и у2 = -х — 1.
Заметим, что если f ‘( a ) не существует, то касательная или не существует (как у функции f (х) = |х| в точке (0; 0) — рис. а, или вертикальна (как у функции 
в точке (0; 0) — рис. б.
Итак, существование производной функции f (х) в точке а эквивалентно существованию невертикальной касательной в точке (а; f (а)) графика. При этом угловой коэффициент касательной равен f ‘(а). В этом заключается геометрический смысл производной.
Понятие производной позволяет проводить приближенные вычисления. Уже неоднократно отмечалось, что при Δх → 0 значения функции f ( x ) и касательной к ней у(х) практически совпадают. Поэтому при Δх → 0 поведение функции f (х) в окрестности точки х0 приближенно можно описать формулой 
(фактически уравнение касательной). Эта формула с успехом используется для приближенных вычислений.
Вычислим значение функции 
в точке х = 2,03.
Найдем производную данной функции: f ‘(х) = 12х2 — 4х + 3. Будем считать, что х = а + Δх, где а = 2 и Δх = 0,03. Вычислим значения функции и ее производной в точке а и получим: 
и 
Теперь определим значение функции в заданной точке х = 2,03. Имеем: 
Разумеется, приведенную формулу удобно использовать, если значения f (а) и f ‘( a ) легко вычислить.
Вычислим 
Рассмотрим функцию 
Найдем производную: 
Будем считать, что х = а + Δх, где а = 8 и Δх = 0,03. Вычислим значения функции и ее производной в точке а и получим: 
Теперь определим значение функции в заданной точке х = 8,03. Имеем: 
Обобщим полученный результат. Рассмотрим степенную функцию f (х) = х n и будем считать, что х = а + Δх и Δх → 0. Найдем f ‘(х) = n х n -1 и вычислим значения функции и ее производной в точке а, получим: f ( a ) = an и f ’( a ) = nan -1 . Теперь имеем формулу f (х) = а n + nan -1 Δх. Применим ее для вычисления числа 0,98-20. Будем считать, что a = 1, Δх = -0,02 и n = -20. Тогда получим: 
Разумеется, приведенную формулу можно использовать и для любых других функций, в частности тригонометрических.
Рассмотрим функцию f ( x ) = tg x и найдем производную: 
Будем считать, что х = a + Δ х, где a = 45° = π/4 и 
(еще раз обратим внимание на то, что в тригонометрии углы обычно измеряют в радианах). Найдем значения функции и ее производной в точке а и получим: 
Теперь вычислим 
(учтено, что π = 3,14).
IV. Контрольные вопросы
1. Уравнение касательной к графику функции.
2. Алгоритм выведения уравнения касательной.
3. Геометрический смысл производной.
4. Применение уравнения касательной для приближенных вычислений.
V. Задание на уроках
§ 29, № 1 (а); 2 (б); 5 (а, б); 6 (в, г); 9 (а); 10 (б); 12 (г); 14 (а); 17; 21 (а); 22 (а, в); 24 (а, б); 25 (а); 26.
VI. Задание на дом
§ 29, № 1 (б); 2 (в); 5 (в, г); 6 (а, б); 9 (б); 10 (а); 12 (б); 14 (б); 18; 21 (в); 22 (б, г); 24 (в, г); 25 (б); 27.
VII. Творческие задания
1. В каких точках х касательные к графикам функций 
параллельны?
Ответ: х = -1, х = 3.
2. При каких х касательные к графикам функций у = 3 cos 5 x — 7 и у = 5 cos 3 x + 4 параллельны?
Ответ: 
3. Под какими углами пересекаются кривые у = х2 и 
Ответ: π/2 и arctg 3/5.
4. Под какими углами пересекаются кривые у = cos x и у = sin х ?
Ответ: 
5. К параболе у = 4 — х2 в точке с абсциссой х = 1 проведена касательная. Найдите точку пересечения этой касательной с осью ординат.
6. К параболе у = 4х — х2 в точке с абсциссой х = 3 проведена касательная. Найдите точку пересечения этой касательной с осью абсцисс.
7. Найдите угол между двумя касательными, проведенными из точки (0; -2) к параболе у = х2.
Ответ: 
8. К графику функции у = 3х2 + 3х + 2 проведены касательные с угловыми коэффициентами k 1 = 0 и k 2 = 15. Напишите уравнение прямой, проходящей через точки касания.
Ответ: у = 12х — 4.
9. Найдите уравнения прямых, касающихся одновременно парабол у = х2 + х — 2 и у = -х2 + 7х — 11.
Ответ: у = 7х — 11 и у = х — 2.
10. Напишите уравнение общей касательной к параболам у = -3х2 + 4х + 4 и у = -3х2 + 16х — 20.
11. Касательная к графику функции у = х2 — 4х — 3 проведена в точке х = 0. Найдите площадь треугольника, образованного касательной и осями координат.
12. Найдите площадь треугольника, ограниченного осями координат и касательной к графику функции 
в точке х = 2.
Узнать ещё
Знание — сила. Познавательная информация
Касательная параллельна прямой
Задания из №7 ЕГЭ, в которых известно, что касательная к графику функции параллельна данной прямой, могут быть связаны как с графиком функции, так и с графиком производной. Поэтому очень важно внимательно читать условие.
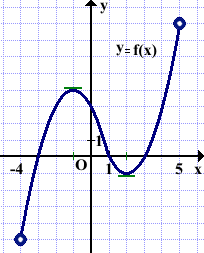
1) На рисунке изображен график функции y=f(x), определённой на интервале(-4;8). Найти количество точек, в которых касательная к графику функции параллельна прямой y=12 или совпадает с ней.
Касательная к графику функции параллельна оси абсцисс, а значит, и любой прямой вида y=b, где b — число, в точках экстремума, в которых производная существует, и в точках перегиба. То есть это задание аналогично заданию на определение точек графика функции, в которых производная равна нулю.
На графике данной функции y=f(x) таких точке две (с абсциссами x=-1 и x=2). Значит, касательная к графику функции параллельна прямой y=12 в двух точках.
Теперь рассмотрим аналогичное задание, в котором дан график производной функции.
2)На рисунке изображён график производной функции f(x), определённой на интервале (-4;8). Найти количество точек, в которых касательная к графику функции параллельна прямой y=12 или совпадает с ней.
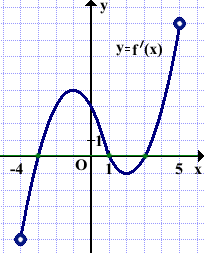
Угловой коэффициент касательной равен значению производной в точке касания: k2=f'(xo).
Значит, ищем точки, в которых значение производной равно нулю.
Таких точек три (с абсциссами x=-3, x=1 и x=3).
3)На рисунке изображён график производной функции f(x), определённой на интервале (-4;8). Найти количество точек, в которых касательная к графику функции параллельна прямой y=3x-11 или совпадает с ней.
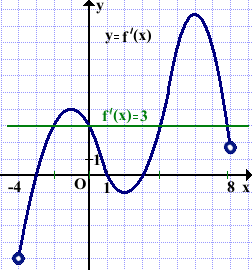
Поэтому ищем точки, в которых значение производной равно 3.
Таких точек в данном примере четыре.
4)На рисунке изображён график производной функции f(x). Найти абсциссу точки, в которой касательная к графику y=f(x) параллельна прямой y=4-x или совпадает с ней.
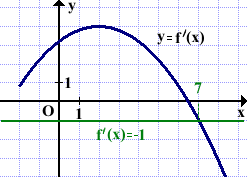
Ищем точку, в которой значение производной равно -1. Абсцисса этой точки xo=7.