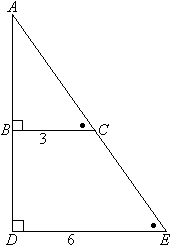На рисунке подобными треугольниками будут

Геометрия | 5 — 9 классы

B8. На рисунке подобными треугольниками будут.

OKM и OKN(по общему катету OK).

Видео:Задачи с подобными треугольникамиСкачать

Окружность проходящая через вершины А и В треугольника ABC пересекает стороны АС и ВС в точках Л и К соответственно доказать что треугольники ABC и СКЛ подобны?

Окружность проходящая через вершины А и В треугольника ABC пересекает стороны АС и ВС в точках Л и К соответственно доказать что треугольники ABC и СКЛ подобны.

С рисунком плиииз.

Видео:Подобие треугольников. Вся тема за 9 минут | ОГЭ по математике | Молодой РепетиторСкачать

Будут ли подобны два треугольника , если длины сторон треугольника соответсвенно равны 10 м , 20 м , 12, 5 м и 100см, 90 см , 160см?

Будут ли подобны два треугольника , если длины сторон треугольника соответсвенно равны 10 м , 20 м , 12, 5 м и 100см, 90 см , 160см.

Видео:Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

Эти треугольники подобны?

Эти треугольники подобны!

Какая сторона какой подобна?

Видео:Первый признак подобия треугольников. Найти подобные по рисунку. Задачи на подобиеСкачать

В трапеции проведены диагонали AC и BD ?

В трапеции проведены диагонали AC и BD .

Тогда треугольники BOC и DOA будут : а ) подобны по двум углам : б ) подобны по двум пропорциональным сторонам и углу мужду ними ; в ) подобны по трем пропорциональным сторонам ; г : не подобны.

Видео:Геометрия Укажите пары подобных треугольников, изображенных на рисунке, найдите длину отрезка xСкачать

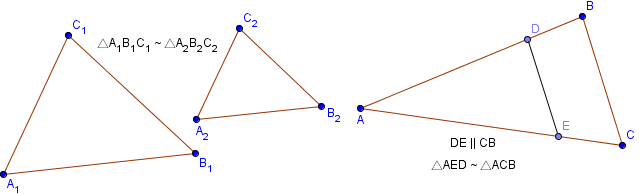
Докажите, что треугольники, изображенные на рисунке подобны, и выясните взаимное расположение прямых AB и DE?

Докажите, что треугольники, изображенные на рисунке подобны, и выясните взаимное расположение прямых AB и DE.

Видео:Задача на подобие треугольников. А ты сможешь решить? | TutorOnline | МатематикаСкачать

На рисунке отрезки am и by являются высотами треугольника abc ?

На рисунке отрезки am и by являются высотами треугольника abc .

Докажите что треугольники cbh и cam подобны.

Видео:Как ПОНЯТЬ ГЕОМЕТРИЮ за 5 минут — Подобие ТреугольниковСкачать

По первому признаку подобия треугольников (если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны) будут подобны любые два ?

По первому признаку подобия треугольников (если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны) будут подобны любые два .

Видео:8 класс, 21 урок, Отношение площадей подобных треугольниковСкачать

Подобны ли два треугольника, если?

Подобны ли два треугольника, если.

Видео:ПОДОБНЫЕ ТРЕУГОЛЬНИКИ . §12 геометрия 8 классСкачать

Докажите что треугольники на рисунке подобны?

Докажите что треугольники на рисунке подобны.

Видео:Если кое-что заметить, то решение будет быстрым ★ Найдите площади двух треугольников на рисункеСкачать

На рисунке изображены прямоугольные треугольники с прямыми углами C и K?

На рисунке изображены прямоугольные треугольники с прямыми углами C и K.

Найдите подобные треугольники и докажите их подобие.

Вы зашли на страницу вопроса B8. На рисунке подобными треугольниками будут?, который относится к категории Геометрия. По уровню сложности вопрос соответствует учебной программе для учащихся 5 — 9 классов. В этой же категории вы найдете ответ и на другие, похожие вопросы по теме, найти который можно с помощью автоматической системы «умный поиск». Интересную информацию можно найти в комментариях-ответах пользователей, с которыми есть обратная связь для обсуждения темы. Если предложенные варианты ответов не удовлетворяют, создайте свой вариант запроса в верхней строке.

Верные ответы : а) вектор ВС = вектор АD г) |вектор АС| = |вектор DB|.

АС = АВ + АДДВ = АВ — АДвот ответ.

Для решения данной задачи необходимо перевести единицы измерения из см в мм т. Е. 10, 4 см = 104 мм АВ — АС = ВС 104 — 76 = 28 мм или 2, 8 см Ответ 28 мм или 2, 8 см.

(180 — 86) 2 = 47° — меньший угол 180 — 47 = 133° — больший угол.

Взаимное расположение 3а + 3а = 6а (оба из одной точки) их длинны равны сумма 3а — 3а = 0.

Одна из особенностей Земли — наличие в ее строении внешних и внутрен­них оболочек. Ближайшие к Земле планеты почти полностью или совсем утратили внешние оболочки. Во всех оболочках Земли интенсивно протекают при­родные процессы, создающие необычайн..

136 : 17 = 8 = R V = 1 / 3ПR в квадр * h Получает треугольник 17 = гипотенуза 8 это катет. По теореме Пифагора = 15 это высота. V = 1 / 3 * 64 * 15 = 320.

А) т. К КЕ биссектриса, то угол МКЕ = углу ЕКР. А т. к. Фигула параллелограмм и стороны попарно параллельны, то угол ЕКР = углу МЕК ( как накрест лежащие) . Отсюда углы при основании равны, следовательно труегольник равнобедренный. Б) т. К. МЕ ..

В равнобедренном треугольнике ABC : AB = BC = 2√13 (см) — боковые стороны AC — основание BD = 6 (cм) — высота, проведенная к основанию AD = CD = AC / 2 т. К высота равнобедренного треугольника, проведенная к основанию, также является медианой Прямоу..

Видео:Решение задач на тему "Подобные треугольники". 8 классСкачать

Подобные треугольники

Видео:Как находить площадь любой фигуры? Геометрия | МатематикаСкачать

Определение

Как правило, два треугольника считаются подобными если они имеют одинаковую форму, даже если они различаются размерами, повернуты или даже перевернуты.

Математическое представление двух подобных треугольников A₁B₁C₁ и A₂B₂C₂ , показанных на рисунке, записывается следующим образом:

Два треугольника являются подобными если:

1. Каждый угол одного треугольника равен соответствующему углу другого треугольника:
∠A₁ = ∠A₂, ∠B₁ = ∠B₂ и∠C₁ = ∠C₂

2. Отношения сторон одного треугольника к соответствующим сторонам другого треугольника равны между собой:
$frac=frac=frac$

3. Отношения двух сторон одного треугольника к соответствующим сторонам другого треугольника равны между собой и при этом
углы между этими сторонами равны:
$frac=frac$ и $angle A_1 = angle A_2$
или
$frac=frac$ и $angle B_1 = angle B_2$
или
$frac=frac$ и $angle C_1 = angle C_2$

Не нужно путать подобные треугольники с равными треугольниками. У равных треугольников равны соответствующие длины сторон. Поэтому для равных треугольников:

Из этого следует что все равные треугольники являются подобными. Однако не все подобные треугольники являются равными.

Несмотря на то, что вышеприведенная запись показывает, что для выяснения, являются ли два треугольника подобными или нет, нам должны быть известны величины трех углов или длины трех сторон каждого треугольника, для решения задач с подобными треугольниками достаточно знать любые три величины из указанных выше для каждого треугольника. Эти величины могут составлять различные комбинации:

1) три угла каждого треугольника (длины сторон треугольников знать не нужно).

Или хотя бы 2 угла одного треугольника должны быть равны 2-м углам другого треугольника.
Так как если 2 угла равны, то третий угол также будет равным.(Величина третьего угла составляет 180 — угол1 — угол2)

2) длины сторон каждого треугольника (углы знать не нужно);

3) длины двух сторон и угол между ними.

Далее мы рассмотрим решение некоторых задач с подобными треугольниками. Сначала мы рассмотрим задачи, которые можно решить непосредственным использованием вышеуказанных правил, а затем обсудим некоторые практические задачи, которые решаются по методу подобных треугольников.

Видео:Как выглядеть стройнее с помощью одежды [25 хаков, которые реально работают]Скачать

Практические задачи с подобными треугольниками

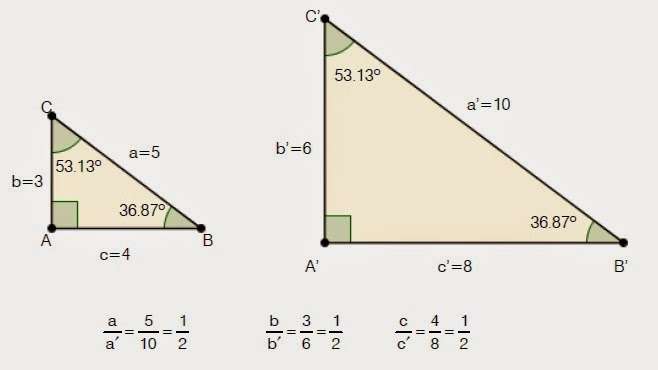
Пример №1: Покажите, что два треугольника на рисунке внизу являются подобными.

Решение:
Так как длины сторон обоих треугольников известны, то здесь можно применить второе правило:

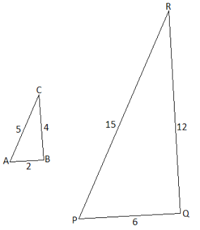
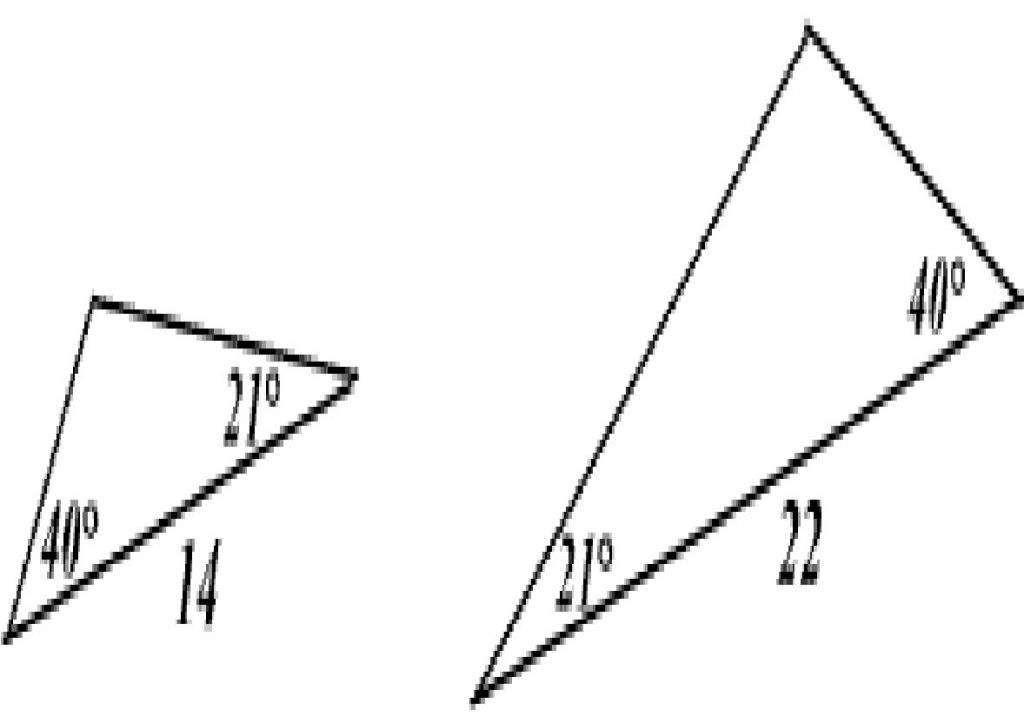
Пример №2: Покажите, что два данных треугольника являются подобными и определите длины сторон PQ и PR.

Решение:
∠A = ∠P и ∠B = ∠Q, ∠C = ∠R(так как ∠C = 180 — ∠A — ∠B и ∠R = 180 — ∠P — ∠Q)

Из этого следует, что треугольники ΔABC и ΔPQR подобны. Следовательно:
$frac=frac=frac$

Пример №3: Определите длину AB в данном треугольнике.

Решение:

∠ABC = ∠ADE, ∠ACB = ∠AED и ∠A общий => треугольники ΔABC и ΔADE являются подобными.

$frac = frac = frac = frac = frac = frac Rightarrow 2times AB = AB + 4 Rightarrow AB = 4$

Пример №4:Определить длину AD (x) геометрической фигуры на рисунке.

Треугольники ΔABC и ΔCDE являются подобными так как AB || DE и у них общий верхний угол C.
Мы видим, что один треугольник является масштабированной версией другого. Однако нам нужно это доказать математически.

AB || DE, CD || AC и BC || EC
∠BAC = ∠EDC и ∠ABC = ∠DEC

Исходя из вышеизложенного и учитывая наличие общего угла C, мы можем утверждать, что треугольники ΔABC и ΔCDE подобны.

Следовательно:
$frac = frac = frac = frac Rightarrow CA = frac = 23.57$
x = AC — DC = 23.57 — 15 = 8.57

Практические примеры

Пример №5: На фабрике используется наклонная конвеерная лента для транспортировки продукции с уровня 1 на уровень 2, который выше уровня 1 на 3 метра, как показано на рисунке. Наклонный конвеер обслуживается с одного конца до уровня 1 и с другого конца до рабочего места, расположенного на расстоянии 8 метров от рабочей точки уровня 1.

Фабрика хочет модернизировать конвеер для доступа к новому уровню, который находится на расстоянии 9 метров над уровнем 1, и при этом сохранить угол наклона конвеера.

Определите расстояние, на котором нужно установить новый рабочий пункт для обеспечения работы конвеера на его новом конце на уровне 2. Также вычислите дополнительное расстояние, которое пройдет продукция при перемещении на новый уровень.

Решение:

Для начала давайте обозначим каждую точку пересечения определенной буквой, как показано на рисунке.

Исходя из рассуждений, приведенных выше в предыдущих примерах, мы можем сделать вывод о том, что треугольники ΔABC и ΔADE являются подобными. Следовательно,

$frac = frac = frac = frac Rightarrow AB = frac = 24 м$
x = AB — 8 = 24 — 8 = 16 м

Таким образом, новый пункт должен быть установлен на расстоянии 16 метров от уже существующего пункта.

А так как конструкция состоит из прямоугольных треугольников, мы можем вычислить расстояние перемещения продукции следующим образом:

Аналогично, $AC = sqrt = sqrt = 25.63 м$
что является расстоянием, которое проходит продукция в данный момент при попадании на существующий уровень.

y = AC — AE = 25.63 — 8.54 = 17.09 м
это дополнительное расстояние, которое должна пройти продукция для достижения нового уровня.

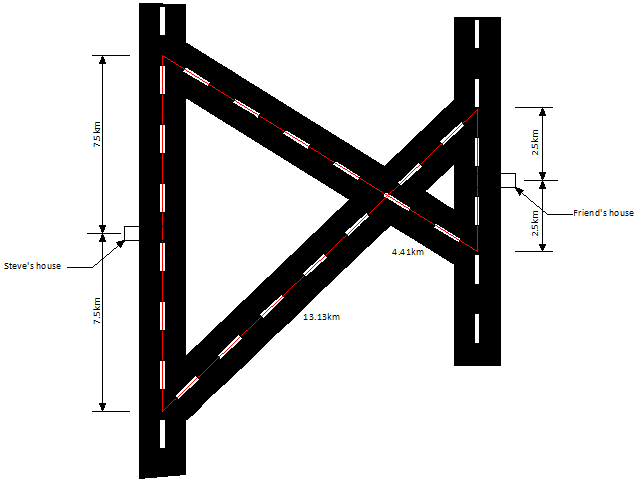
Пример №6: Стив хочет навестить своего приятеля, который недавно переехал в новый дом. Дорожная карта проезда к дому Стива и его приятеля вместе с известными Стиву расстояниями показана на рисунке. Помогите Стиву добраться к дому его приятеля наиболее коротким путем.

Решение:

Дорожную карту можно геометрически представить в следующем виде, как показано на рисунке.

Мы видим, что треугольники ΔABC и ΔCDE подобны, следовательно:
$frac = frac = frac$

В условии задачи сказано, что:

AB = 15 км, AC = 13.13 км, CD = 4.41 км и DE = 5 км

Используя эту информацию, мы можем вычислить следующие расстояния:

Стив может добраться к дому своего друга по следующим маршрутам:

A -> B -> C -> E -> G, суммарное расстояние равно 7.5+13.23+4.38+2.5=27.61 км

F -> B -> C -> D -> G, суммарное расстояние равно 7.5+13.23+4.41+2.5=27.64 км

F -> A -> C -> E -> G, суммарное расстояние равно 7.5+13.13+4.38+2.5=27.51 км

F -> A -> C -> D -> G, суммарное расстояние равно 7.5+13.13+4.41+2.5=27.54 км

Следовательно, маршрут №3 является наиболее коротким и может быть предложен Стиву.

Пример 7:
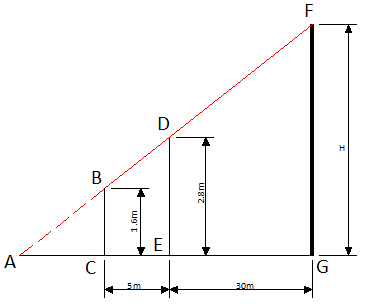
Триша хочет измерить высоту дома, но у нее нет нужных инструментов. Она заметила, что перед домом растет дерево и решила применить свою находчивость и знания геометрии, полученные в школе, для определения высоты здания. Она измерила расстояние от дерева до дома, результат составил 30 м. Затем она встала перед деревом и начала отходить назад, пока верхний край здания стал виден над верхушкой дерева. Триша отметила это место и измерила расстояние от него до дерева. Это расстояние составило 5 м.

Высота дерева равна 2.8 м, а высота уровня глаз Триши равна 1.6 м. Помогите Трише определить высоту здания.

Решение:

Геометрическое представление задачи показано на рисунке.

Сначала мы используем подобность треугольников ΔABC и ΔADE.

$frac = frac = frac = frac Rightarrow 2.8 times AC = 1.6 times (5 + AC) = 8 + 1.6 times AC$

$(2.8 — 1.6) times AC = 8 Rightarrow AC = frac = 6.67$

Затем мы можем использовать подобность треугольников ΔACB и ΔAFG или ΔADE и ΔAFG. Давайте выберем первый вариант.

Видео:Подобные треугольникиСкачать

Признаки подобия и равенства треугольников. Свойства подобных треугольников

Треугольник является самой простой замкнутой фигурой на плоскости. При изучении школьного курса геометрии рассмотрению его свойств уделяют особое внимание. В данной статье раскроем вопрос признаков подобия и равенства треугольников.

Видео:ПОДОБНЫЕ ТРЕУГОЛЬНИКИ 😉 #егэ #математика #профильныйегэ #shorts #огэСкачать

Какие треугольники называются подобными, а какие равными?

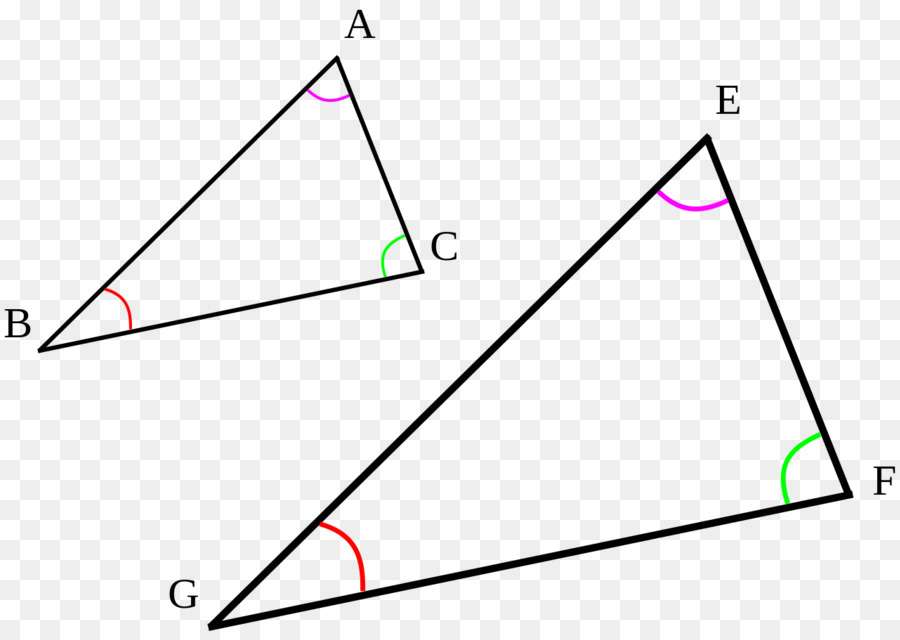
Логично предположить, что две рассматриваемые фигуры будут равны между собой, если они имеют все одинаковые углы и длины сторон. Что касается подобия, то здесь дело обстоит немного сложнее. Два треугольника будут подобны тогда, когда каждый угол одного будет равен соответствующему углу другого, а стороны, лежащие напротив равных углов обеих фигур, будут пропорциональны. Ниже изображен рисунок, на котором представлены два подобных треугольника.

Вам будет интересно: Полемизировать – это значит, спорить правильно

Используя этот рисунок, запишем в виде математических равенств данное выше определение: B = G, A = E, C = F, BA / GE = AC / EF = BC / GF = r, здесь одна латинская буква означает угол, а две буквы — длину стороны. Величина r носит название коэффициента подобия. Понятно, что если r = 1, то имеют место не только подобные, но и равные треугольники.

Видео:Подобные треугольники - 8 класс геометрияСкачать

Признаки подобия

Говоря о свойствах и признаках подобия и равенства треугольников, следует перечислить три основных критерия, по которым можно определить, являются ли рассматриваемые фигуры подобными или нет.

Итак, две фигуры будут подобными между собой, если выполняется одно из следующих условий:

Все три стороны взаимно пропорциональны. Излагая математическим языком, получаем: BA / GE = AC / EF = BC / GF = r, тогда рассматриваемые фигуры тоже являются подобными.

Отметим еще раз, что для доказательства подобия достаточно привести какой-либо один из представленных признаков. Логично, что все остальные будут выполняться также.

Видео:КТО ЛУЧШЕ НАРИСУЕТ ПРЕДМЕТ ГЕОМЕТРИЧЕСКИМИ ФИГУРАМИ, ПОЛУЧИТ ЭТО ЧЕЛЛЕНДЖ !Скачать

Прямоугольные треугольники: когда они подобны, а когда равны?

Говоря о признаках равенства и подобия прямоугольных треугольников, следует отметить сразу, что у каждого из них по одному углу уже равны (90o).

Последний факт приводит к следующей формулировке изложенных выше критериев подобия:

Наконец, пропорциональности всего двух любых сторон для обоих прямоугольных треугольников достаточно для доказательства их подобия. Причина этого заключается в том, что стороны данных фигур связаны между собой теоремой Пифагора, поэтому пропорциональность 2-х из них приводит к пропорциональности с аналогичным коэффициентом подобия и для третьих сторон.

Что касается равенства треугольников с прямыми углами, то здесь просто запомнить: если два каких-либо элемента (прямой угол не считается) обеих фигур равны, то равны и сами фигуры. Например, этими двумя элементами могут быть острый угол и катет, катет и гипотенуза или гипотенуза и острый угол.

Видео:Подобные треугольники с нуля до ОГЭ | Математика ОГЭ 2023 | УмскулСкачать

Свойства треугольников подобных

Из рассмотренных признаков подобия и равенства треугольников свойства можно выделить такие:

Площади подобных фигур относятся как квадрат коэффициента подобия, то есть: S1 / S2 = r2, где S1 и S2 — площади 1-го и 2-го треугольников, соответственно.

Оба эти свойства можно доказать самостоятельно. Суть доказательства сводится к применению математической записи подобия между сторонами фигур. Здесь приведем лишь доказательство 1-го свойства.

Пусть a, b, c — длины сторон одного треугольника и a’, b’, c’ — стороны второго. Поскольку фигуры подобны, то можно записать: a = r * a’, b = r * b’, c = r * c’. Теперь эти выражения подставим в отношении их периметров, получим: P1 / P2 = (a + b + c) / (a’ + b’ + c’) = (r * a’ + r * b’ + r*c’) / (a’ + b’ + c’) = r(a’ + b’ + c’) / (a’ + b’ + c’) = r.

Видео:8 класс, 20 урок, Определение подобных треугольниковСкачать

Пример решения задачи

Признаки подобия и равенства треугольников можно использовать для решения различных геометрических задач. Ниже приводится один из примеров.

Имеются два треугольника. У одного из них стороны равны 7,6 см, 4,18 см и 6,65 см, а у другого 3,5 см, 2,2 см и 4 см. Необходимо определить, подобны ли эти фигуры.

Поскольку даны значения трех сторон, то можно сразу проверить 3-й критерий подобия. Сложность здесь состоит в том, что нужно понять, между какими сторонами брать отношения. Тут следует воспользоваться простыми логическими рассуждениями: коэффициенты подобия могут быть равными, если делить самую маленькую сторону одного треугольника на аналогичную для другого и так далее. Поэтому имеем: 4,18 / 2,2 = 1,9; 6,65 / 3,5 = 1,9; 7,6 / 4 = 1,9. Проверив отношение всех сторон, можно с уверенностью сказать, что треугольники являются подобными, поскольку выполняется 3-й критерий.

🌟 Видео

Задачи с подобными треугольниками 2Скачать