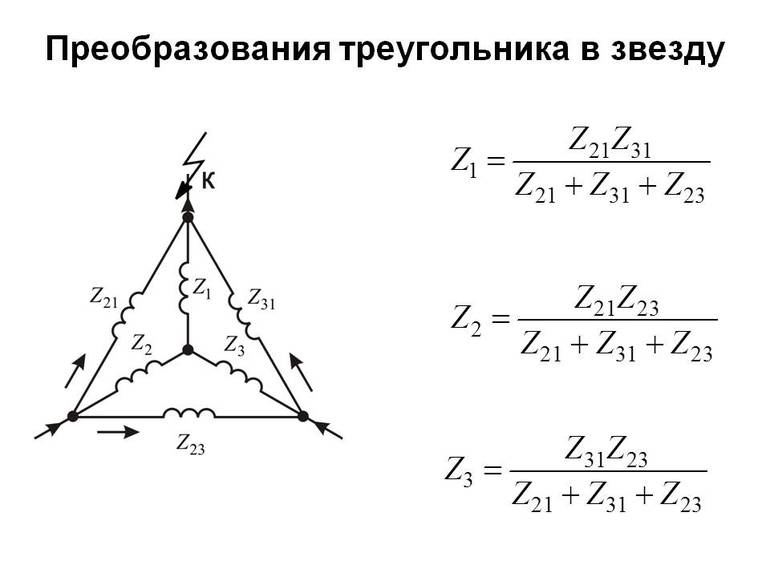
Задачи преобразование треугольник звезда (6 видео)

Задачи преобразование треугольник звезда

Преобразования треугольник-звезда и звезда-треугольник

Во многих схемах можно встретить такие конфигурации компонентов, в которых невозможно выделить последовательные или параллельные цепи. К этим конфигурациям относятся соединения компонентов в виде звезды (Y) и треугольника (Δ):

Очень часто, в ходе анализа электрических цепей, оказывается полезным преобразовать треугольник в звезду или, наоборот, звезду в треугольник. Практически, чаще возникает необходимость преобразования треугольника в звезду. Если при замене одной из этих схем другой не изменяются потенциалы одноименных точек и подтекающие к ним токи, то во внешней цепи также не произойдет никаких изменений. Иными словами, эквивалентные Δ и Y цепи ведут себя одинаково.

Существует несколько уравнений, используемых для преобразования одной цепи в другую:

Δ и Y цепи очень часто встречаются в 3-фазных сетях переменного тока, но там они, как правило, сбалансированы (все резисторы равны по значению) и преобразование одной цепи в другую не требует таких сложных расчетов. Тогда возникает вопрос: где мы сможем использовать эти уравнения?

Использовать их можно в несбалансированных мостовых схемах:

Анализ данной схемы при помощи Метода Токов Ветвей или Метода Контурных Токов довольно сложен. Теорема Миллмана и Теорема Наложения здесь тоже не помощники, так как в схеме имеется только один источник питания. Можно было бы использовать теорему Тевенина или Нортона, выбрав в качестве нагрузки резистор R₃, но и здесь у нас вряд ли что-нибудь получится.

Помочь в этой ситуации нам сможет преобразование треугольник — звезда. Итак, давайте выберем конфигурацию резисторов R₁, R₂ и R₃, представляющих собой треугольник (R_ab, R_ac и R_bc соответственно), и преобразуем ее в звезду:

После преобразования схема примет следующий вид:

В результате преобразования у нас получилась простая последовательно-параллельная цепь. Если мы правильно выполним расчеты, то напряжения между точками А, В и С преобразованной схемы будут аналогичны напряжениям между этими же точками исходной схемы, и мы сможем вернуть их обратно.

Сопротивления резисторов R₄ и R₅ остаются неизменными: 18 и 12 Ом соответственно. Применив к схеме последовательно-параллельный анализ, мы получим следующие значения:

Теперь, используя значения напряжений из приведенной выше таблицы, нам нужно рассчитать напряжения между точками А, В и С. Для этого мы применим обычную математическую операцию сложения (или вычитания для напряжения между точками В и С):

Переносим эти напряжения в исходную схему (между точками А, В и С):

Напряжение на резисторах R₄ и R₅ останется таким же, каким оно было в преобразованной схеме.

К данному моменту у нас есть все необходимые данные для определения токов через резисторы (используем для этой цели Закон Ома I = U / R):

Моделирование при помощи программы PSPICE подтвердит наши расчеты:

Содержание

Преобразование треугольника в звезду — методы, формулы и примеры
Общие сведения
Переход треугольник — звезда
Обратное преобразование
Решение примера
Преобразование и расчет цепей с помощью перехода «звезда» ? «треугольник»
1.9. Преобразование и расчет цепей с помощью перехода «звезда» ? «треугольник»
1.10. Расчет цепей по правилам Кирхгофа
🌟 Видео

Видео:урок 2 Преобразование треугольника сопротивлений в звездуСкачать

Преобразование треугольника в звезду — методы, формулы и примеры

Видео:Лекция 24. Преобразование треугольника в звезду.Скачать

Общие сведения

Электрическая цепь предназначена для обеспечения протекания по ней токов определённой величины. Она содержит источники и приёмники энергии, которые соединены проводниками. При изображении радиоэлементов используют их графические обозначения. Электрические же соединения обозначают прямыми линиями. Замкнутые проводники образовывают контуры. В их состав входят узлы (точки контакта трёх и более линий) и ветви (соединители).

Существует 2 способа обеспечения контакта между элементами:

параллельный — при таком включении в цепи не будет ни одного узла;
последовательный — входящие в цепь эквиваленты присоединены к одной точке, связанной или не имеющей контакта с другой.

В основе преобразований лежит приведение схемы к упрощённому виду без изменения величины тока или напряжения. Для этого выделяют один контур и заменяют его эквивалентным сопротивлением. При последовательном соединении импеданс просто складывают, а вот при параллельном используют формулу: 1/R = 1/R1 + 1/R2 +…1/Rn.

Таким образом, путем замены пары элементов одним, схема последовательно упрощается до тех пор, пока в ней не окажется один резистор. А уже по его величине и рассчитывают ток цепи. Но в некоторых случаях существуют соединения, которые не поддаются методу упрощения. Если внимательно посмотреть на такую цепь, можно увидеть подключение, похожее на треугольник. В таком случае невозможно определить, какие элементы параллельные, а какие последовательные.

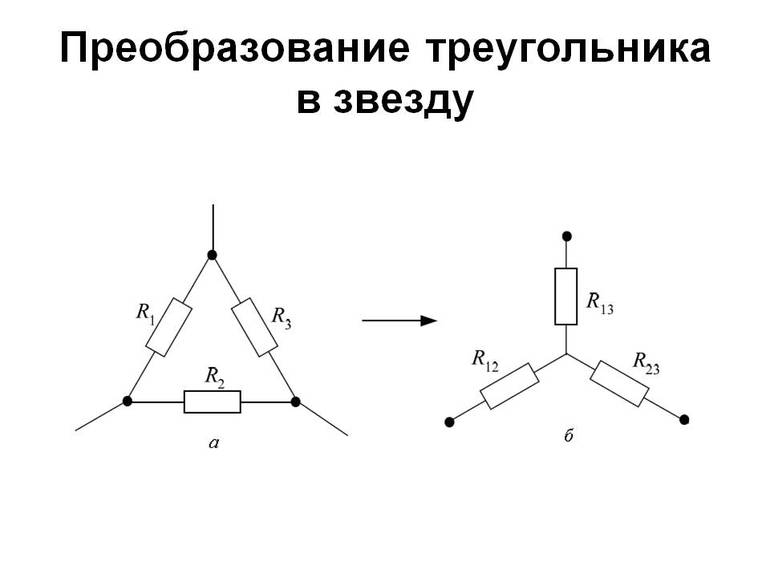
Чтобы найти эквивалентное сопротивление таких сложных соединений, используют преобразование треугольника в равнозначную звезду. По сути, при треугольном подключении 3 элемента образуют замкнутый контур. При этом между каждой парой резисторов имеется узел. Связь же звездой образуется при получении трёх лучевого соединения, в котором каждый элемент цепи подсоединён одним концом к общему узлу, а другой стороной контакта к остальной части схемы.

Преобразование в физике выполняют по строго установленным формулам.

Если его выполнить правильно, значения потенциалов в одноимённых точках треугольника и звёзды, а также подводящиеся к этим узлам токи, останутся одинаковыми. Это значит, что вся оставшаяся часть схемы «не заметит» выполненной замены.

Видео:Преобразование звезды сопротивлений в эквивалентный треугольник. Преобразование мостовой схемыСкачать

Переход треугольник — звезда

Чтобы преобразовать треугольник в звезду, нужно применять особый подход. Закон Ома для такого случая применить невозможно, поэтому упрощения выполняют, руководствуясь правилами Киргофа. Их 2. Первое гласит, что в узле токи компенсируют друг друга, то есть их алгебраическая сумма равняется нулю. Второе же сообщает, что если сложить электродвижущую силу в любом замкнутом контуре цепи, она будет равна алгебраической сумме падений потенциала на импедансе этой части схемы.

В соответствии с этими законами, можно утверждать, что в узлах электрического заряда нет. Он не расходуется и не собирается. В количественном виде первое утверждение записывают так: I1 = I2 + I3, где с левой стороны стоит значение тока втекающего, а справа вытекающих. Второй закон описывается выражением: E1 — Е2 = -UR1 — UR2 или E1 = Е2 — UR1 — UR2.

Опираясь на эти правила, можно выполнить перевод схемы.

Сделать это удобно, руководствуясь следующим алгоритмом:

Пусть имеется контур, образованный из резисторов Ra1, Rb1, Rc1, соединённых треугольником.
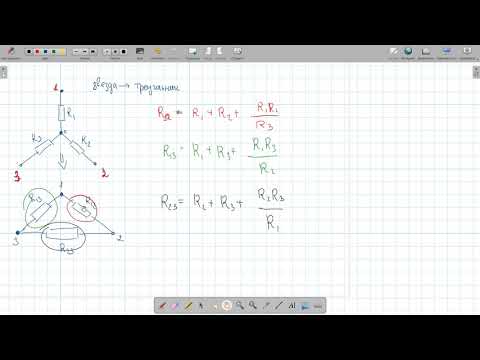
Сумму всех сопротивлений можно обозначить символом RΔ. Её можно будет найти, сложив все импедансы: RΔ = Ra1 + Rb1 + Rc1.
Для получения равенства с неизвестными нужно сделать перестановку в соотношении. Выражение примет вид: Ra2 + (RΔs)Rb2 + (RΔs)Rc2 = Ra1 * Rb1 + Rb1 * Rc1.
Из эквивалентных уравнений можно вывести ещё 2 формулы, описывающие оставшиеся пары контактов. Беря во внимание симметрию, можно получить: Ra2 + (0)Rb2 + (RΔs)Rc2 = Ra1 * Rс1 + Rb1 * Rc1 и Ra2 + (RΔs)Rb2 + (0)Rc2 = Ra1 * Rc1 + Ra1 * Rb1.
Нужно выполнить сложение последних двух уравнений, а после, отняв первое, получить равенство: 2 (RΔs) * Ra2 = 2 * Ra1 * Rc1. Отсюда: Ra2 = Ra1 * Rc1 / RΔs.
По аналогии можно найти и оставшиеся эквиваленты: Rb2 = Ra1 * Rb1 / RΔs и Rc2 = Rc1 * Rb1 / RΔs.

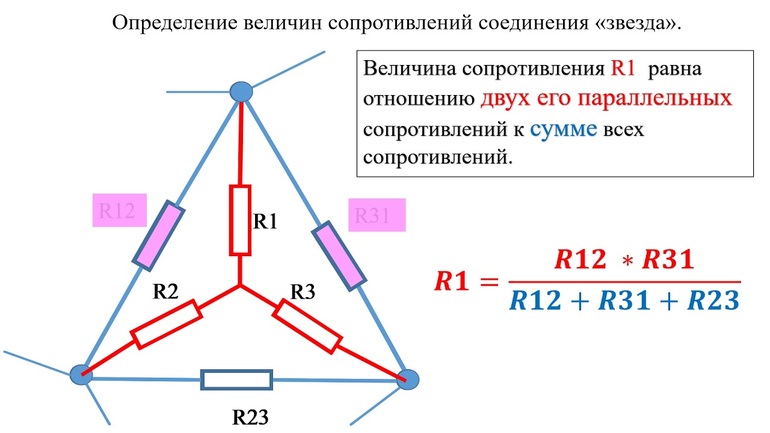
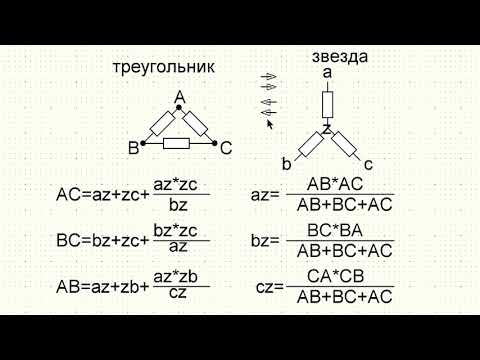
Конечно же, при решении задачи о переводе из одного вида подключения в другое никто не расписывает промежуточные вычисления, а используют сразу конечную формулу: Rk = Rk1 * Rk2 / RΔs, где: Rk — сопротивление, подключённое к контакту в уже трансформированной схеме, а Rk1 и Rk2 — резисторы, стоящие в контуре типа треугольник.

Таким образом, сопротивление, соединённое с каждым узлом при переходе, можно найти из перемножения сопротивлений, подключённых к соответствующей точке в цепи, подключённой треугольником, и дальнейшему их делению на сумму всех резисторов в неизменном контуре.

Видео:022+ Практика, преобразование из треугольника в эквивалентную звездуСкачать

Обратное преобразование

Чтобы получить нужную формулу, следует вести ряд обозначений. Токи, подходящие к узлам, можно обозначить как I1, I2, I3. Преобразование должно выполняться таким образом, чтобы при замене контура величины других токов и потенциалов не изменялись. Для этого следует выразить упорядоченное движение зарядов через напряжение точек и проводимость.

В соответствии с первым правилом Кирхгофа, можно записать: I1 + I2 + I3 = 0. Равенство можно изменить так: (f1 — f0) * p1 + (f2 — f0) * p1 + (f2 — f0) * p1 = 0, где: f — потенциал в точке. В выражении легко выполнить простые преобразования и найти f0. Оно будет равно: f0 = (f1p1 + f2p2 + f3p3) / (p1 + p2 + p3). Полученную формулу возможно использовать для вывода тока. Для I1 будет верным уравнение: I1 = (f1 — f0) * p1 = (f1 * (p2 + p3) — f2 * p2 — f3p3) * p / (p1 + p2 + p3).

Движение заряда удобно обозначать не буквами, а цифрами. Например, число 12 будет показывать, что рассматривается связь первого и второго узла. Таким образом, в треугольнике I1 = I12 — I31 = (f1 — f2) * p12 — (f3 — f1) * p13 = f1* (p12 + p13) — f3p13 -f 2p12.

Учитывая, что ток I1 в схеме треугольник и звезда одинаков, при этом величины потенциалов не влияют на его значение, коэффициенты, стоящие возле f в правой и левой части, будут равны. Тогда можно записать следующие равенства: p12 = p1 * p2 / (p1 + p2 + p3); p13 = p1 * p3 / (p1 + p2 + p3); p23 = p2 * p2 / (p1 + p2 + p3). Как раз по этим формулам и возможно рассчитать проводимость треугольника через звезду.

Зная проводимость, можно определить импеданс, так как это величина обратна сопротивлению. Вывод формулы будет иметь следующий вид: R12 = (1/r1 + 1/r2 + 1/r3) / 1/r1 * r2. Для дальнейших расчётов многочлен (1/r1 + 1/r2 + 1/r3) удобно заменить одной буквой, например, s. Тогда: R12 = s / r3; R23 = s / r1; R13 = s / r2. Подставив последние выражения в формулу для нахождения s, можно будет получить отношение: m = (r12 * r23 * r31) / (r12 + r23 + r31).

Формулы для нахождения эквивалента при переходе примут вид:

R1 = (r12 * r31) / y;
R2 = (r23 * r12) / y;
R3 = (r13 * r23) / y.

Где: y = r12 + r23 + r31. Полезность преобразования в треугольник позволяет привести схему к набору простых последовательных соединений. Подключение двигателей по этой схеме позволяет добиться наибольшей отдачи мощности, например, при модернизации промышленных электросетей.

Видео:Лекция 25. Преобразование звезды в треугольник.Скачать

Решение примера

При знании формул решение задач на преобразование треугольника в звезду или обратно обычно не доставляет проблем. Нужно просто внимательно следить за подставляемыми величинами. Но перед тем как приступить непосредственно к расчёту эквивалентной схемы, следует оценить необходимость выполнения такого действия. Некоторые элементы могут быть соединены последовательно или параллельно, поэтому нужно будет начать с простых преобразований, а уже позже переходить к звезде или треугольнику.

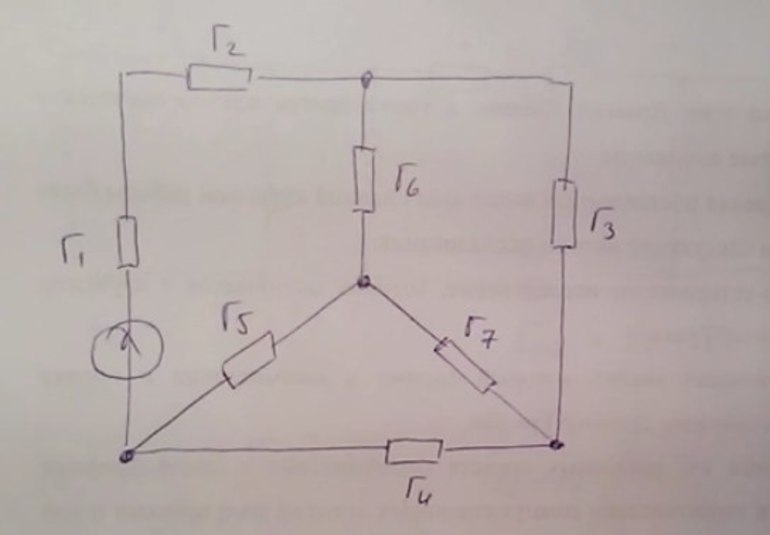
Вот пример задания. Имеется трёхфазная цепь. Посчитать её эквивалентное сопротивление. Известно, что схема подключена к источнику напряжения 220 вольт, сопротивление: R1 = 10 Ом, R2 = 20 Ом, R3 = 30 Ом, R4 = 40 Ом, R5 = 50 Ом, R6 = 60 Ом, R7 = 70 Ом.

В этой схеме сопротивления R1 и R2 соединены последовательно. Что же касается остальных элементов, сказать, какой тип подключения у них по отношению друг к другу, нельзя. Но зато видно, что контур, состоящий из R5, R7, R4, является треугольником, то есть задача состоит в превращении его в эквивалентную трёхлучевую звезду.

Новые элементы можно обозначить как R57, R45, R47. Чтобы найти номиналы новых сопротивлений, нужно воспользоваться эквивалентными формулами. R57 = (R5 * R7) / R5 + R4 + R7 = 50 * 70 / 50 + 40 + 70 = 3500 / 160 = 21,8 Ом; R45 = (R4 * R5) / R5 + R4 + R7 = 40 * 50 / 50 + 40 + 70 = 2000 / 160 = 12,5 Ом; R47 = (R4 * R7) / R5 + R4 + R7 = 40 * 70 / 50 + 40 + 70 = 2800 / 160 = 17,5 Ом.

Теперь эквивалентный контур можно подставить в схему вместо треугольника. В результате цепь будет состоять из трёх последовательно соединённых резисторов R1, R2 и R45. Общий импеданс для них будет равен: Rx = R1 + R2 + R45 = 10 + 20 + 17,5 = 47,5 Ом. Аналогично можно вычислить параметр и для второго контура: Ry = R6 + R57 = 60 + 21,8 = 81,8 Ом. Останется найти сопротивление ветви, включающую R3 и R47, Rz = R3 + R47 = 30 + 17,5 = 47,5 Ом.

Теперь схема принимает довольно простой вид. Контур состоит из трёх включённых параллельно относительно друг друга резисторов Rx, Ry, Rz. Если использовать формулу нахождения эквивалента для такого типа включения, результирующее первое сопротивление будет равно: Rоб = Ry * Rz / (Ry + Rz) = 81,8 * 47,5 / (81,8 + 47,5) = 3885,5 / 129,3 = 30,05 Ом. Теперь схема уже стала одноконтурной и содержит соединение, которое будет называться последовательным.

Таким образом, эквивалентное сопротивление для схемы будет составлять: Rx + R об = 30,05 + 47,5 = 77,55 Ом. Задача решена.

Видео:Как находить общее сопротивление цепей. Преобразование треугольника в звездуСкачать

Преобразование и расчет цепей с помощью перехода «звезда» ? «треугольник»

1.9. Преобразование и расчет цепей с помощью перехода «звезда» ? «треугольник»

Задача 1: В электрических цепях (рис. 1 и 2) сопротивление RAB между зажимами A и B и сопротивление RCD между зажимами C и D равны, а сопротивления резисторов R1, R2 и R3 ? заданы. Найдите все возможные значения сопротивления Rx.

Вначале немного теории:
Рассматриваемый метод основан на том, что сложную схему, имеющую три вывода (узла), можно заменить другой, с тем же числом выводов (узлов). Замену следует произвести так, чтобы сопротивление участка между двумя любыми выводами новой схемы было таким же, как у прежней. В результате получится цепь, сопротивление которой эквивалентно сопротивлению данной по условию. Общее сопротивление обеих цепей будет одинаковым. Однако, поскольку в результате такого преобразования изменяются токи внутри цепи, такую замену можно проводить только в тех случаях, когда не надо находить распределение токов.
Подобные преобразования широко известны для случая двух выводов. Так, например, два резистора сопротивлениями R1 и R2, включенные последовательно (Рис. 1), можно заменить одним резистором сопротивлением

Если резисторы включены параллельно (Рис. 2), то их можно заменить одним резистором сопротивлением

И в этих случаях распределение токов в цепи (или в части цепи) претерпевает изменения.
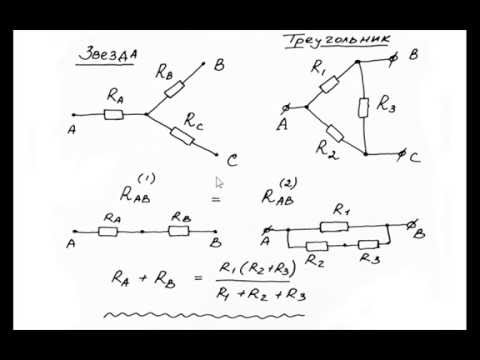
Рассмотрим более сложное преобразование схем, имеющих три вывода (трехполюсников). Иначе это называется преобразованием «звезды» (Рис. 3) в «треугольник» (Рис. 4), и наоборот.

Сопротивления резисторов в схеме «звезда» обозначаются с индексом точки, с которой соединен этот резистор, например, резистор r1 соединен с точкой 1. В «треугольнике» индексы резисторов соответствуют точкам, между которыми они включены, например, резистор R13 подключен к точкам 1 и 3.
Как отмечено выше, чтобы заменить одну из этих схем другой, нужно получить такие соотношения между их сопротивлениями, чтобы эквивалентные сопротивления между любыми точками были одинаковы для обеих схем (при условии сохранения числа этих точек).
Так, в «звезде» сопротивление между точками 1 и 2 равно r1 + r2, в «треугольнике»

Следовательно, для того чтобы сопротивления между точками 1 и 2 были одинаковы для обеих схем, необходимо, чтобы выполнялось следующее равенство:

Аналогично для точек 2 и 3 и для точек 1 и 3.

Сложим все эти уравнения и, поделив обе части на 2, получим:

Вычитая из этого уравнения поочередно предыдущие, получим:

Эти выражения легко запомнить:
знаменатель в каждой формуле есть сумма сопротивлений всех резисторов «треугольника», а в числителе дважды повторяется индекс, стоящий слева:

Аналогично получают и формулы обратного преобразования:

Последние выражения также легко запомнить и проверить: числитель у всех уравнений один и тот же, а в знаменателе стоит сопротивление резистора с индексом, которого не достает в левой части выражения.
Этот метод представляет собой наиболее универсальный подход к решению практически всех типов задач на разветвленные цепи.
А теперь приступим к решению задачи:

Наиболее просто сопротивления RAB и RCD можно вычислить, если соединение «треугольником» резисторов R1, R2 и Rx (на рисунках 5 и 6 оно обведено пунктирным контуром) заменить эквивалентным соединением «звездой» (рис. 7 и 8).

На данном этапе мы воздержимся от пересчета «треугольника» в «звезду», а будем считать, что rA, r1 и r2 нами уже найдены. Поскольку RAB = RCD, то и RMB = RND, так как rA соединено последовательно с каждым из них:

Так как в последнем уравнении знаменатели равны, то должны быть равны и числители:

(rx + R3)(r2 + Rx) = (rx + Rx)(r2 + R3).

После раскрытия скобок и приведения подобных членов это уравнение примет вид

Такое равенство возможно в двух случаях:

Rx = R3 ? это один корень уравнения; r1 = r2.

Данное равенство указывает на симметрию соединения «звездой», но симметрия «звезды» возможна только тогда, когда и исходная схема соединения «треугольником» обладает подобной симметрией, то есть когда R1 = Rx ? это второй корень уравнения. Других решений у составленного нами уравнения нет. Следовательно, возможны только два значения Rx:

Rx = R1 и Rx = R3.

При внимательном анализе схем (рис. 1 и 2) оба решения легко «угадываются», но их единственность не очевидна.

Для закрепления понимания метода решите следующую задачу:
Задача 2: В схеме неуравновешенного моста (рис. 9) определите общее сопротивление цепи между точками А и С, если R1 = 1 Ом, R2 = 1,6 Ом, R3 = 2 Ом, R4 = 1,2 Ом, R5 = 2 Ом.

Подсказка Преобразуйте соединение треугольник в звезду. ответ RAC = 1,5 Ом.

1.10. Расчет цепей по правилам Кирхгофа

Два правила Кирхгофа представляют собой довольно сложный алгоритм решения задач на нахождение любых характеристик цепи постоянного тока. Причем сложность заключена обычно не в составлении и записи уравнений, а в решении системы большого числа (не менее трех) этих уравнений.
Первое правило Кирхгофа.
Алгебраическая сумма токов в любой точке разветвления проводников (в узле) равна нулю.
Токи, втекающие в узел А цепи (рис. 1),

будем, например, считать положительными, тогда вытекающие из узла токи ? отрицательные; запишем:

Выделим в произвольной цепи произвольный замкнутый контур (рис. 2).

Второе правило Кирхгофа.
Для замкнутого контура сумма произведений сил токов в отдельных участках этого контура на соответствующие сопротивления равна алгебраической сумме ЭДС, действующих в этом контуре.
Для контура, изображенного на рис. 2, запишем:

С помощью правил Кирхгофа составляется система линейных алгебраических уравнений, число которых равно числу неизвестных физических параметров в задачах с разветвленной электрической цепью. Рекомендуем следующий алгоритм:

выберите направление токов во всех участках разветвленной цепи и отметьте их на чертеже; составьте уравнения по первому правилу Кирхгофа, соблюдая правило знаков: токи, втекающие в узел, ? положительные, вытекающие из узла, ? отрицательные; убедитесь, что число составленных уравнений на единицу меньше числа узлов в цепи; произвольно выберите контур и направление его обхода; каждый новый контур должен содержать хотя бы одну новую ветвь цепи; при обходе контура и составлении уравнения соблюдайте правило знаков: ток противоположного направления обхода берется со знаком «минус»; при записи алгебраической суммы ЭДС следуйте мнемоническому правилу последнего знака: при переходе через источник «ЭДС берется с последним знаком»; проверьте полноту системы полученных уравнений и решите ее; если значение некоторых токов в цепи получилось отрицательным, значит, ток течет в направлении, противоположном обозначенному на схеме. Если же получено отрицательное значение сопротивления, то ответ ошибочный.

Рассмотрим пример.
Задача 1. Определите сопротивление цепи АВ (рис. 3), если R1 = R5 = 1 Ом, R2 = R6 = 2 Ом, R3 = R7 = 3 Ом, R4 = R5 = 4 Ом.

Решение.
В данной цепи, состоящей из восьми резисторов, нет хотя бы двух элементов, соединенных между собой последовательно или параллельно. Кроме того, здесь в отличие от схем, рассмотренных ранее, отсутствует осевая симметрия (она имела бы место, если бы сопротивления всех резисторов были одинаковы). Используем правила Кирхгофа. Для этого предположим, что к зажимам цепи АВ подключен источник постоянного тока (показано пунктиром). Обозначим токи на всех участках цепи и произвольно укажем их направления. Всего их получается 9: I1, I2, I3, I4, I5, I6, I7, I8, I.
Чтобы избежать громоздких вычислений, связанных с решением системы из девяти уравнений, воспользуемся следующим обстоятельством: из условия задачи видно, что данная цепь обладает центральной симметрией с центром в точке О. Действительно, если, отсоединив цепь в точках А и В от источника, повернуть се в плоскости чертежа вокруг точки О на 180° и снова соединить с источником, то в силу данных в условии равенств она совместится со своим первоначальным положением.
Но теперь в резисторе R5 течет ток, который был раньше в резисторе R1. Перемена же знаков напряжения на зажимах не может вызвать изменения силы тока ни на одном участке цепи. Это означает, что и раньше в резисторах R5 и R1 текли токи одинаковой силы, т. е. I1 = I5.
Аналогично можно показать, что в данной цени должны выполняться равенства: I2 = I6; I3 = I7; I4 = I8.
Таким образом, в задаче фактически имеется лишь пять неизвестных токов: I1, I2, I3, I4, I. Тогда, по первому правилу Кирхгофа, с учетом того, что I2 = I6, I4 = I8 получим соответственно для узлов А, С и D три уравнения:

Легко убедиться проверкой, что аналогичные уравнения, составленные для остальных трех узлов схемы, будут повторением уже имеющихся уравнений, что является следствием осевой симметрии сопротивлений резисторов схемы. Недостающие два уравнения можно получить на основании второго правила Кирхгофа.
Выбрав направление обхода контуров по часовой стрелке, запишем, например, для контуров ACDBEA и АСЕА уравнения:

Подставив в эти уравнения численные значения сопротивлений из условия задачи и учитывая, что I8R8 = I4R4, решим систему из пяти уравнений относительно тока I и получим:

Но так как I = E/R то отсюда следует значение искомого эквивалентного сопротивления: R = 47/14 Ом.
Как было отмечено выше, любая сложная цепь может быть рассчитана с помощью двух правил Кирхгофа. Помимо положительных сторон данного метода необходимо отметить и ряд неудобств, громоздкость вычислений ? основное из них. Так, при решении приведенной задачи расчет был искусственно упрощен за счет симметричности данных и осевой симметрии схемы относительно точки О. Кроме того, не приведен полный расчет системы полученных уравнений, а дан лишь конечный результат. Если бы в условии задачи все резисторы имели бы разные величины, то пришлось бы решать систему из девяти уравнений с девятью неизвестными, что само по себе весьма неудобно.

Задача 2. В цепи E1 = 4 B, E2 = 3 B, r1 = 2 Ом, r2 = 1 Ом, R = 10 Ом (рис.). Найдите силу тока в резисторе R.

Решение:
Воспользуемся правилами Кирхгофа. Для их применения необходимо знать направление токов в каждом участке цепи.
Возможны два варианта: или ток течет слева направо или, наоборот, справа налево. Надо определиться, допустим, направление тока такое как показано на рисунке.
По первому правилу Кирхгофа (для узла А) I1 = I2 + Ix.
По второму правилу Кирхгофа (для замкнутых контуров AE1BA и ABE2A), выбрав за положительное направление обход контуров против хода часовой стрелки, получим

Из системы записанных уравнений найдем ток

Знак минус в полученном результате означает, что сделанное предположение о направлении тока Ix в резисторе R оказалось неверным. Ток в резисторе течет не слева направо, а в обратном направлении. Сила этого тока 1/16 A.

Задача 3. Дана цепь (рис. 6). Составьте основные уравнения для данной цепи.

Задача 4. Три источника тока с ЭДС Е1 = 11 В, Е2 = 4 В и Е3 = 6 В и три резистора с сопротивлением R1 = 5 Ом, R2 = 10 Ом и R3 = 2 Ом соединены, как показано на рисунке 7. Определите силы токов I в резисторах. Внутренним сопротивлением источников пренебречь.