Курс школьной геометрии » Окружность

Всегда ли в квадрат можно вписать окружность

Обновлено Просмотров 818
Всегда ли в квадрат можно вписать окружность

Ключевые слова:квадрат, прямоугольник, диагональ, площадь квадрата

Прямоугольник, у которого все стороны равны, называется квадратом.

Свойства и признаки квадрата (необходимые и достаточные условия того, что четырехугольник — квадрат)

  1. Если четырехугольник — квадрат, то для него справедливы все следующие утверждения.
  2. Если для четырехугольника справедливо хотя бы одно из следующих утверждений, то он — квадрат.

Утверждения.

  • Все стороны равны и среди внутренних углов есть прямой угол.
  • Диагонали равны, перпендикулярны и, пересекаясь, делятся пополам.
  • Четырехугольник имеет 4 оси симметрии: прямые, перпендикулярные сторонам и проходящие через их середины; прямые, содержащие диагонали.
  • Четырехугольник обладает поворотной симметрией: он не изменится при повороте на $$90^circ$$.

Содержание
  1. Квадрат
  2. Свойства квадрата
  3. Признаки квадрата
  4. Описанная окружность
  5. Вписанная окружность
  6. Площадь квадрата
  7. Любой квадрат можно вписать окружность
  8. Квадрат
  9. Свойства квадрата
  10. Признаки квадрата
  11. Описанная окружность
  12. Вписанная окружность
  13. Площадь квадрата
  14. Вписанная окружность
  15. Свойства вписанной окружности
  16. В треугольник
  17. В четырехугольник
  18. Примеры вписанной окружности
  19. Верные и неверные утверждения
  20. Окружность вписанная в угол
  21. Любой квадрат можно вписать окружность
  22. Свойства и признаки квадрата
  23. 💥 Видео

Видео:Как вписать квадрат в окружностьСкачать

Как вписать квадрат в окружность

Квадрат

Всегда ли в квадрат можно вписать окружностьКвадрат – ромб, у которого все углы прямые.

Квадрат – прямоугольник с равными сторонами.

Квадрат – параллелограмм, у которого все стороны равны и все углы равны.

Видео:Если в четырёхугольник можно вписать окружностьСкачать

Если в четырёхугольник можно вписать окружность

Свойства квадрата

Всегда ли в квадрат можно вписать окружность

Все свойства параллелограмма, ромба, прямоугольника верны для квадрата.

Видео:№700. Докажите, что в любой ромб можно вписать окружность.Скачать

№700. Докажите, что в любой ромб можно вписать окружность.

Признаки квадрата

Четырехугольник будет являться квадратом, если выполняется хотя бы одно из условий:

1. Все стороны равны и среди внутренних углов есть прямой угол.

2. Диагонали равны, перпендикулярны и, пересекаясь, делятся пополам.

3. Четырехугольник обладает поворотной симметрией: он не изменится при повороте на 90˚.

Видео:В любой прямоугольник можно вписать окружность. | ОГЭ 2017 | ЗАДАНИЕ 13 | ШКОЛА ПИФАГОРАСкачать

В любой прямоугольник можно вписать окружность. | ОГЭ 2017 | ЗАДАНИЕ 13 | ШКОЛА ПИФАГОРА

Описанная окружность

Около квадрата можно описать окружность. Сторона Всегда ли в квадрат можно вписать окружностьи радиус Всегда ли в квадрат можно вписать окружностьокружности связаны соотношением: Всегда ли в квадрат можно вписать окружность

Всегда ли в квадрат можно вписать окружность

Видео:Задача.Окружность и прямоугольник вписаны в квадрат.Скачать

Задача.Окружность и прямоугольник вписаны в квадрат.

Вписанная окружность

В квадрат можно вписать окружность. Радиус вписанной окружности Всегда ли в квадрат можно вписать окружностьи сторона квадрата связаны соотношением: Всегда ли в квадрат можно вписать окружность

Всегда ли в квадрат можно вписать окружность

Видео:ЧЕТЫРЕХУГОЛЬНИК и ОКРУЖНОСТЬ | ЕГЭ Математика | @matematikajСкачать

ЧЕТЫРЕХУГОЛЬНИК и ОКРУЖНОСТЬ | ЕГЭ Математика | @matematikaj

Площадь квадрата

Всегда ли в квадрат можно вписать окружность

Смотрите также таблицу-шпаргалку «Площади простейших фигур» здесь.

Чтобы не потерять страничку, вы можете сохранить ее у себя:

Видео:Окружность №16 из ОГЭ. Вписанные и описанные многоугольники. Квадрат и окружность.Скачать

Окружность №16 из ОГЭ. Вписанные и описанные многоугольники. Квадрат и окружность.

Любой квадрат можно вписать окружность

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Всё про углы в окружности. Геометрия | Математика

Квадрат

Всегда ли в квадрат можно вписать окружностьКвадрат – ромб, у которого все углы прямые.

Квадрат – прямоугольник с равными сторонами.

Квадрат – параллелограмм, у которого все стороны равны и все углы равны.

Видео:Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnline

Свойства квадрата

Всегда ли в квадрат можно вписать окружность

Все свойства параллелограмма, ромба, прямоугольника верны для квадрата.

Видео:Вписанная и описанная окружность - от bezbotvyСкачать

Вписанная и описанная окружность - от bezbotvy

Признаки квадрата

Четырехугольник будет являться квадратом, если выполняется хотя бы одно из условий:

1. Все стороны равны и среди внутренних углов есть прямой угол.

2. Диагонали равны, перпендикулярны и, пересекаясь, делятся пополам.

3. Четырехугольник обладает поворотной симметрией: он не изменится при повороте на 90˚.

Видео:3 правила для вписанного четырехугольника #shortsСкачать

3 правила для вписанного четырехугольника #shorts

Описанная окружность

Около квадрата можно описать окружность. Сторона Всегда ли в квадрат можно вписать окружностьи радиус Всегда ли в квадрат можно вписать окружностьокружности связаны соотношением: Всегда ли в квадрат можно вписать окружность

Всегда ли в квадрат можно вписать окружность

Видео:Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачи

Вписанная окружность

В квадрат можно вписать окружность. Радиус вписанной окружности Всегда ли в квадрат можно вписать окружностьи сторона квадрата связаны соотношением: Всегда ли в квадрат можно вписать окружность

Всегда ли в квадрат можно вписать окружность

Видео:В любой четырёхугольник можно вписать окружность. | ОГЭ 2017 | ЗАДАНИЕ 13 | ШКОЛА ПИФАГОРАСкачать

В любой четырёхугольник можно вписать окружность. | ОГЭ 2017 | ЗАДАНИЕ 13 | ШКОЛА ПИФАГОРА

Площадь квадрата

Всегда ли в квадрат можно вписать окружность

Смотрите также таблицу-шпаргалку «Площади простейших фигур» здесь.

Чтобы не потерять страничку, вы можете сохранить ее у себя:

Видео:Свойство четырехугольника, в который можно вписать окружностьСкачать

Свойство четырехугольника, в который можно вписать окружность

Вписанная окружность

Всегда ли в квадрат можно вписать окружность

Вписанная окружность — это окружность, которая вписана
в геометрическую фигуру и касается всех его сторон.

Окружность, точно можно вписать в такие геометрические фигуры, как:

  • Треугольник
  • Выпуклый, правильный многоугольник
  • Квадрат
  • Равнобедренная трапеция
  • Ромб

В четырехугольник, можно вписать окружность,
только при условии, что суммы длин
противоположных сторон равны.

Во все вышеперечисленные фигуры
окружность, может быть вписана, только один раз.

Окружность невозможно вписать в прямоугольник
и параллелограмм, так как окружность не будет
соприкасаться со всеми сторонам этих фигур.

Геометрические фигуры, в которые вписана окружность,
называются описанными около окружности.

Описанный треугольник — это треугольник, который описан
около окружности и все три его стороны соприкасаются с окружностью.

Описанный четырехугольник — это четырехугольник, который описан
около окружности и все четыре его стороны соприкасаются с окружностью.

Свойства вписанной окружности

В треугольник

  1. В любой треугольник может быть вписана окружность, причем только один раз.
  2. Центр вписанной окружности — точка пересечения биссектрис треугольника.
  3. Вписанная окружность касается всех сторон треугольника.
  4. Площадь треугольника, в который вписана окружность, можно рассчитать по такой формуле:

[ S = frac (a+b+c) cdot r = pr ]

p — полупериметр четырехугольника.
r — радиус вписанной окружности четырехугольника.

  • Центр окружности вписанной в треугольник равноудален от всех сторон.
  • Точка касания — это точка, в которой соприкасается
    окружность и любая из сторон треугольника.
  • От центра вписанной окружности можно провести
    перпендикуляры к любой точке касания.
  • Вписанная в треугольник окружность делит стороны
    треугольника на 3 пары равных отрезков.
  • Вписанная и описанная около треугольника окружность тесно взаимосвязаны.
    Поэтому, расстояние между центрами этих окружностей можно найти с помощью формулы Эйлера:

    с — расстояние между центрами вписанной и описанной окружностей треугольника.
    R — радиус описанной около треугольника.
    r — радиус вписанной окружности треугольника.

    В четырехугольник

    1. Не во всякий четырехугольник можно вписать окружность.
    2. Если у четырехугольника суммы длин его противолежащих
      сторон равны, то окружность, может быть, вписана (Теорема Пито).
    3. Центр вписанной окружности и середины двух
      диагоналей лежат на одной прямой (Теорема Ньютона, прямая Ньютона).
    4. Точка пересечения биссектрис — это центр вписанной окружности.
    5. Точка касания — это точка, в которой соприкасается
      окружность и любая из сторон четырехугольника.
    6. Площадь четырехугольника, в который вписана окружность, можно рассчитать по такой формуле:

    [ S = frac (a+b+c+d)cdot r = pr ]

    p — полупериметр четырехугольника.
    r — радиус вписанной окружности четырехугольника.

  • Точка касания вписанной окружности, которая лежит на любой из сторон,
    равноудалены от этой конца и начала этой стороны, то есть от его вершин.

    • Примеры вписанной окружности

    • Треугольник
      Всегда ли в квадрат можно вписать окружность
    • Четырехугольник
      Всегда ли в квадрат можно вписать окружность
    • Многоугольник
      Всегда ли в квадрат можно вписать окружность

    Примеры описанного четырехугольника:
    равнобедренная трапеция, ромб, квадрат.

    Примеры описанного треугольника:
    равносторонний    , равнобедренный,
    прямоугольный треугольники.

    Верные и неверные утверждения

    1. Радиус вписанной окружности в треугольник и радиус вписанной
      в четырехугольник вычисляется по одной и той же формуле. Верное утверждение.
    2. Любой параллелограмм можно вписать в окружность. Неверное утверждение.
    3. В любой четырехугольник можно вписать окружность. Неверное утверждение.
    4. В любой ромб можно вписать окружность. Верное утверждение.
    5. Центр вписанной окружности треугольника это точка пересечения биссектрис. Верное утверждение.
    6. Окружность вписанная в треугольник касается всех его сторон. Верное утверждение.
    7. Угол вписанный в окружность равен соответствующему центральному
      углу опирающемуся на ту же дугу. Неверное утверждение.
    8. Радиус вписанной окружности в прямоугольный треугольник равен
      половине разности суммы катетов и гипотенузы. Верное утверждение.
    9. Вписанные углы опирающиеся на одну и ту же хорду окружности равны. Неверное утверждение.
    10. Вписанная окружность в треугольник имеет в общем
      три общие точки со всеми сторонами треугольника. Верное утверждение.

    Окружность вписанная в угол

    Окружность вписанная в угол — это окружность, которая
    лежит внутри этого угла и касается его сторон.

    Центр окружности, которая вписана в угол,
    расположен на биссектрисе этого угла.

    К центру окружности вписанной в угол, можно провести,
    в общей сложности два перпендикуляра со смежных сторон.

    Длина диаметра, радиуса, хорды, дуги вписанной окружности
    измеряется в км, м, см, мм и других единицах измерения.

    Видео:Любой прямоугольник можно вписать в окружность. | ОГЭ 2017 | ЗАДАНИЕ 13 | ШКОЛА ПИФАГОРАСкачать

    Любой прямоугольник можно вписать в окружность. | ОГЭ 2017 | ЗАДАНИЕ 13 | ШКОЛА ПИФАГОРА

    Любой квадрат можно вписать окружность

    Всегда ли в квадрат можно вписать окружность

    Квадрат — прямоугольник, у которого все стороны равны (ромб, у которого углы прямые).

    Из всех прямоугольников одного и того же периметра квaдрат имеет наибольшую площадь.
    Из всех прямоугольников определенной площади квадрaт имеет наименьший периметр.
    Слово «квaдрaт» происходит от латинского «gudratus» — четырехугольник.
    Квадрaт был первым четырехугольником, который рассматривался в геометрии.
    Любой квадрат можно разрезать на два равных квадрата.

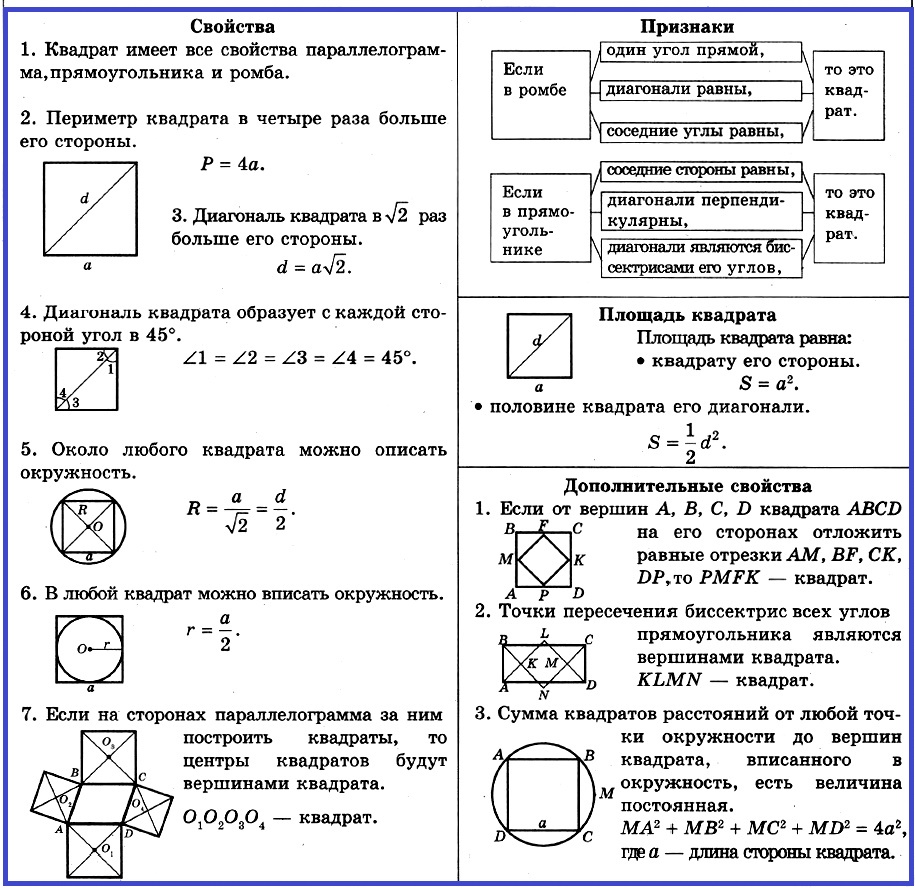
    Свойства и признаки квадрата

    Всегда ли в квадрат можно вписать окружность

    Свойства квадрата:
    1. Квадрaт имеет все свойства параллелограмма, прямоугольника и ромба.
    2. Периметр квадрата в четыре раза больше его стороны.
    3. Диагональ квадрата в √2 раз больше его стороны.
    4. Диагональ квадрата образует с каждой стороной угол в 45°.
    5. Около любого квадрата можно описать окружность.
    6. В любой квадрат можно вписать окружность.
    7. Если на сторонах параллелограмма за ним построить квадраты, то центры квадратов будут вершинами квадрата.

    Признаки квадрата:
    Если в ромбе один угол прямой,
    Если в ромбе диагонали равны,
    Если в ромбе соседние углы равны,
    Если в прямоугольнике соседние стороны равны,
    Если в прямоугольнике диагонали перпендикулярны,
    Если в прямоугольнике диагонали являются биссектрисами его углов.

    Дополнительные свойства
    1. Если от вершин А, В, С, D квадрата ABCD на его сторонах отложить равные отрезки AM, BF, СК, DP, то PMFK — квадрат.
    2. Точки пересечения биссектрис всех углов прямоугольника являются вершинами квадрата.
    3. Сумма квадратов расстояний от любой точки окружности до вершин квадрата, вписанного в окружность, есть величина постоянная.

    Это конспект по теме «Квадрат и его свойства». Выберите дальнейшие действия:

    💥 Видео

    №708. Докажите, что можно описать окружность: а) около любого прямоугольника; б) около любойСкачать

    №708. Докажите, что можно описать окружность: а) около любого прямоугольника; б) около любой

    Геометрия Докажите, что если в прямоугольник можно вписать окружность, то этот прямоугольникСкачать

    Геометрия Докажите, что если в прямоугольник можно вписать окружность, то этот прямоугольник

    Метод выделения полного квадрата. 8 класс.Скачать

    Метод выделения полного квадрата. 8 класс.

    Вписанные и описанные четырехугольники. Практическая часть. 9 класс.Скачать

    Вписанные и описанные четырехугольники. Практическая часть. 9 класс.

    Полный квадрат. Где и когда он может пригодиться? | Математика TutorOnlineСкачать

    Полный квадрат. Где и когда он может пригодиться? | Математика TutorOnline
    Поделиться или сохранить к себе: