Определить истинную величину треугольника совмещением

Метки

Видео:Определение натуральной величины треугольника АВС методом замены плоскостей проекцииСкачать

Натуральная величина треугольника с описанием.

Натуральная величина треугольника определяется 2 методами:

1. замена плоскостей проекции;
2. плоскопараллельное перемещение.

Это задание является обязательным для студентов в учебных заведениях и для его решения необходимо изучить тему: » Способы преобразования чертежа».

Для наглядности я использовал определенное задание и на его примере покажу как находится натуральная величина треугольника.

Алгоритм определения натуральной величины плоскости:

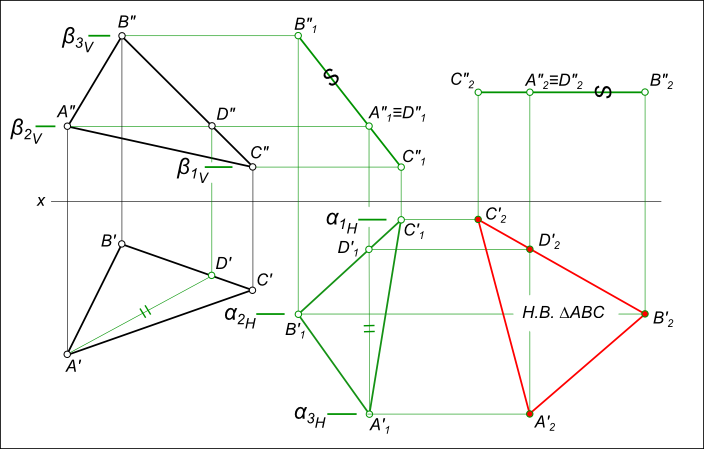
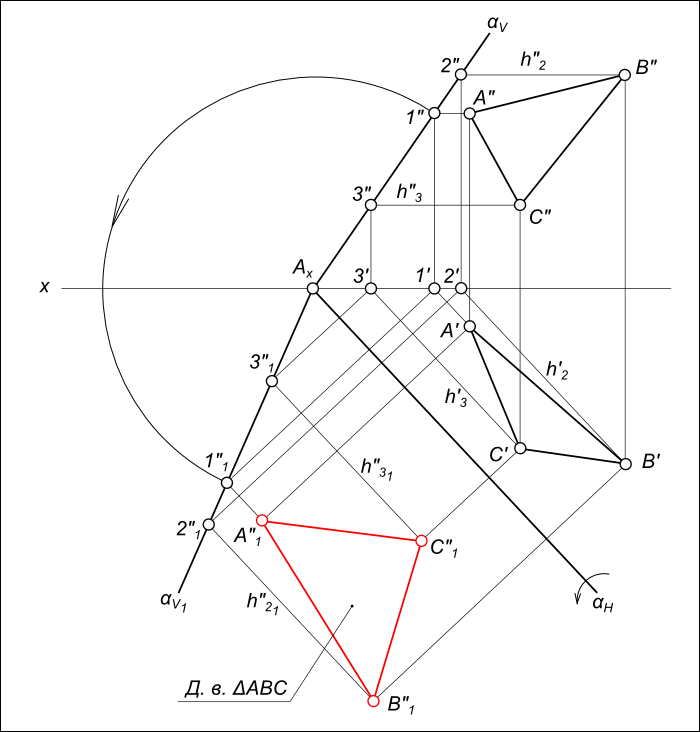
Замена плоскостей проекции

1.) Для построения чертежа использовал задание, расположенное снизу. Первоначально строятся точки по координат в плоскостях П1 и П2.

2.) Строится дополнительная горизонтальная линия 1 1 в верхнем изображении (проводится линия от средне расположенной точки по высоте), затем опускают дополнительные отрезки на нижнее изображение (как указано на рисунке снизу) и соединяют прямой. Эта прямая необходима для того, чтобы на ней расположить вспомогательную плоскость.

3.) Построив прямую на нижнем рисунке, чертится под углом 90 0 ось Х 1 (от точки С1 располагаем на произвольном расстоянии, но не слишком далеко). Затем отмеряются расстояния:

• от С2 до оси Х;
• от В2 до оси Х;
• от А0 до оси Х.

Полученные размеры откладываются от оси Х1 (размеры указаны разными цветами на рисунке снизу) и соединяют, далее подписываются точки.

4.) Строится еще одна дополнительная ось Х2, расположенная параллельно отрезку В 4 С 4 А 4. От точек В4,С4 и А4 проводят прямые перпендикулярные оси Х2.

5.) Отмеряются расстояния:

• от В1 до Х1;
• от С1 до Х1;
• от А1 до Х1.

Полученные результаты измерений откладываются от иси Х2 (на изображении снизу отмечены зелеными и голубым цветами).

6.) Соединяются точки и подписывают полученную плоскость заглавными «Н.В.»

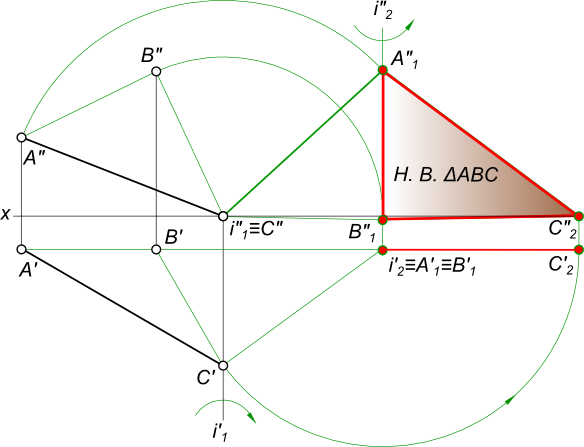
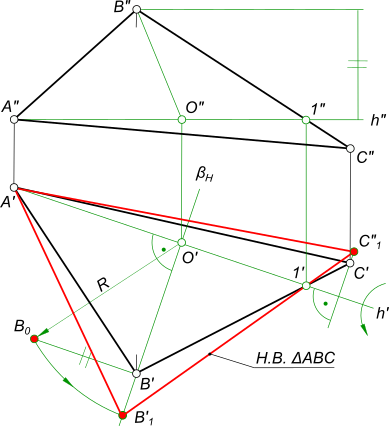
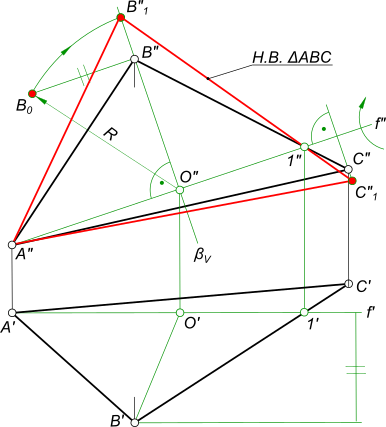
Плоскопараллельное перемещение

7.) Откладывается отрезок на оси Х (обозначен синим цветом).

8.) Переносятся точки на текущее построение.

9.) Соединяют точки, получившиеся при переносе из плоскостей проекций. 10.) Методом вращения точки А2′, С2′ переносятся на горизонтальную прямую, а точка В2′ не меняет свое положение (относительно ее и происходило вращение).11.) Откладывается точка (располагают от оси Х на небольшом расстоянии, т.е. произвольном), относительно которой и будет откладываться плоско параллельное перемещение плоскости. 12.) От точек А2′, С2′ и В2′ опускаются прямые. Далее циркулем необходимо отмерить расстояния:

Затем эти размеры откладываются от С1′ (обозначены красным и синим цветами).

13.) Соединяются и подписываются точки (А1′, В1′ и С1′). Опускают прямые от С2″ и А2″14.) От точек С1 и А1 отводят прямые до пересечения с прямыми опущенными от точек С2″ и А2″. В месте пересечения ставится точка.15.) Завершающим шагом является соединение точек и обводка линиями всего чертежа.Пример чертежа на тему «Натуральная величина треугольника» смотрите здесь.

Видео:Определение натуральной величины треугольника АВС методом вращения вокруг горизонтали или фронталиСкачать

Определить истинную величину треугольника совмещением

Видео:Определение натуральной величины треугольника АВС методом совмещенияСкачать

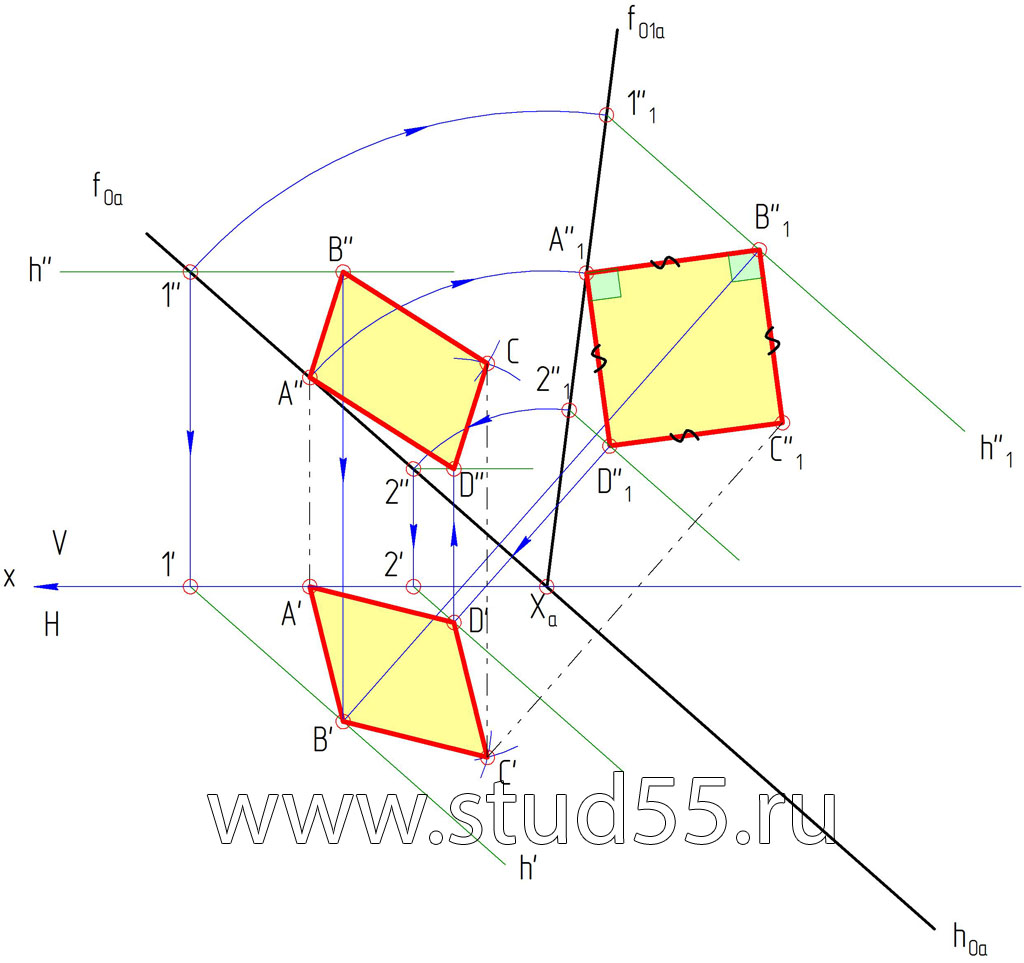
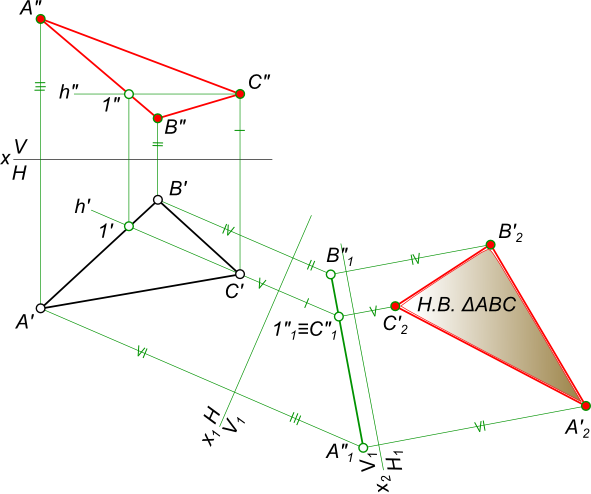
Нахождение натуральной величины способом совмещения

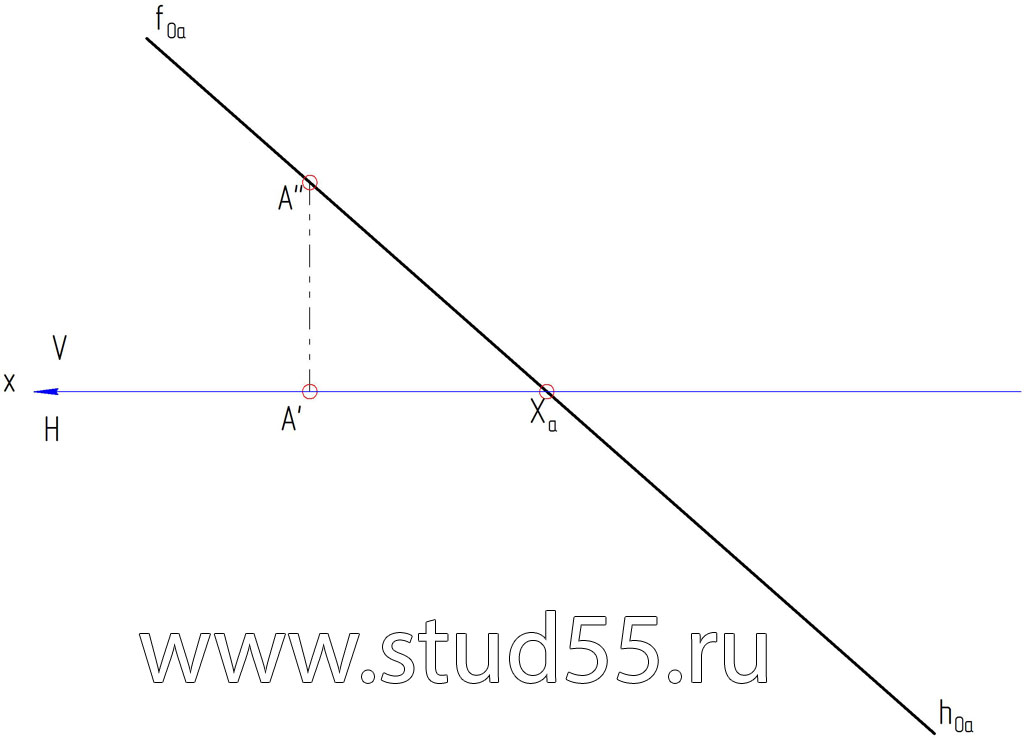
Задача: В плоскости, заданной следами, взять произвольный отрезок АВ. Способом совмещения определить его истинную величину. Принимая отрезок за сторону правильной плоской фигуры (квадрат), построить эту фигуру.

Теория

Способ совмещения заключается в том, что заданную плоскость а (альфа) вместе с расположенными в ней геометрическими элементами вращают вокруг одного из ее следов f_oa или h_oa до совмещения с соответствующей плоскостью проекций Н или V.

Все геометрические элементы (прямые и другие линии, фигуры), лежащие в заданной плоскости, изображаются в натуральную величину на плоскости проекций, с которой производится совмещение. Совмещение позволяет найти величину плоской фигуры по ее проекциям или построить проекции плоской фигуры, лежащей в какой-либо плоскости, по заданным ее размерам.

Пошаговое решение:

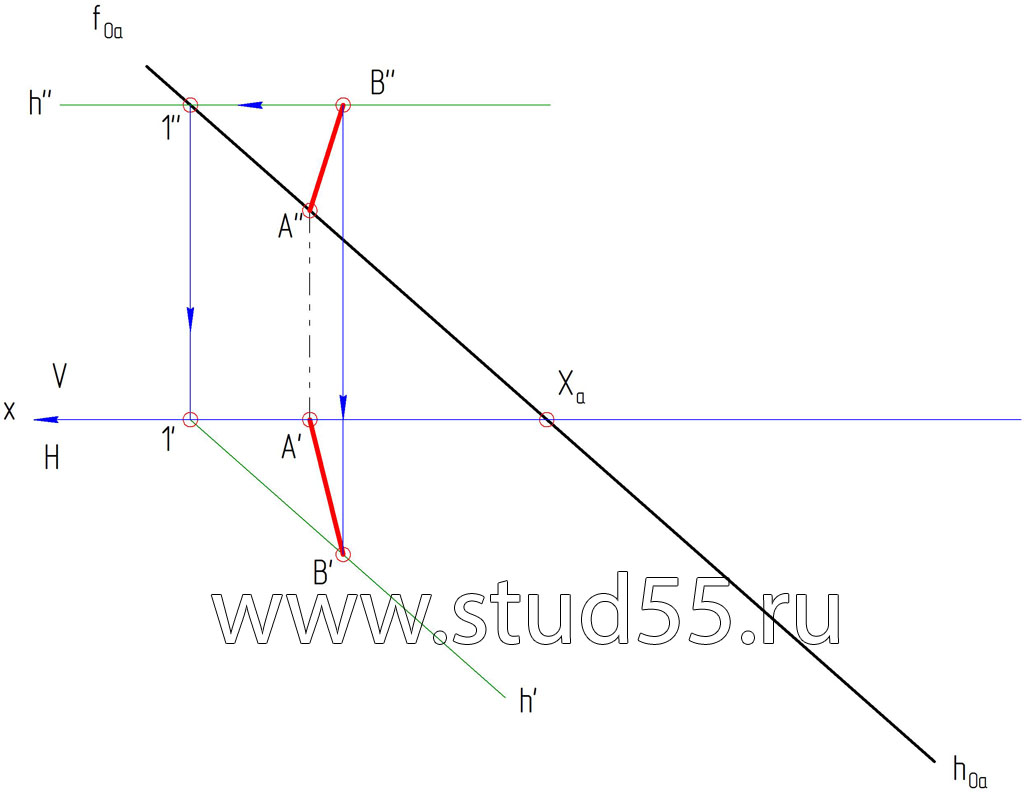
1) Берем произвольную проекцию точки В (B») во фронтальной плоскости V, находим ее проекцию B’ горизонтальной плоскости проекций Н, из у словия, что отрезок АВ лежит в плоскости альфа.

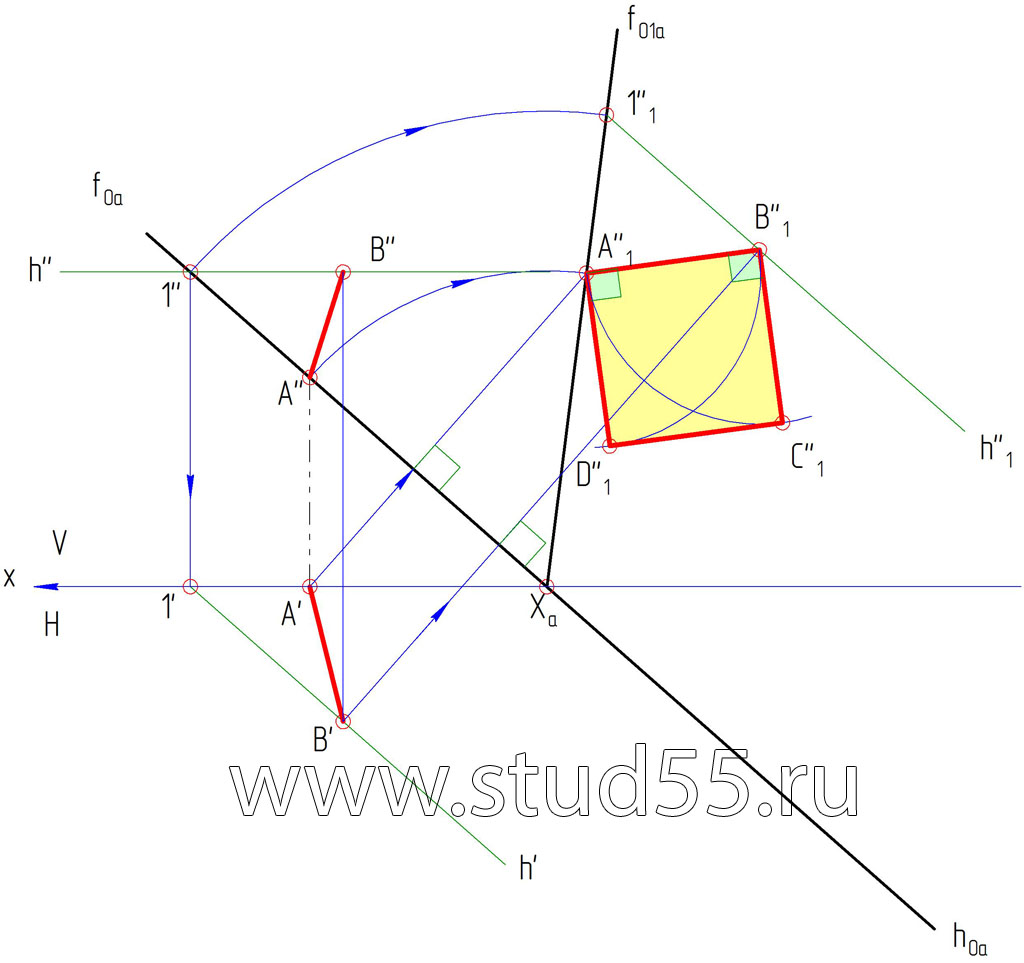
2) Т.к. плоскость задана следами, то задача совмещения ее с плоскостью проекций сводится к построению совмещенного положения одного из следов — f_o1a, так как другой след — h_oa, принимаемый за ось вращения, не меняет своего положения.

Отрезок АВ, лежащий в заданной плоскости, изображается в истинную величину (И.в.) на новой плоскости проекций, с которой мы произвели совмещение.

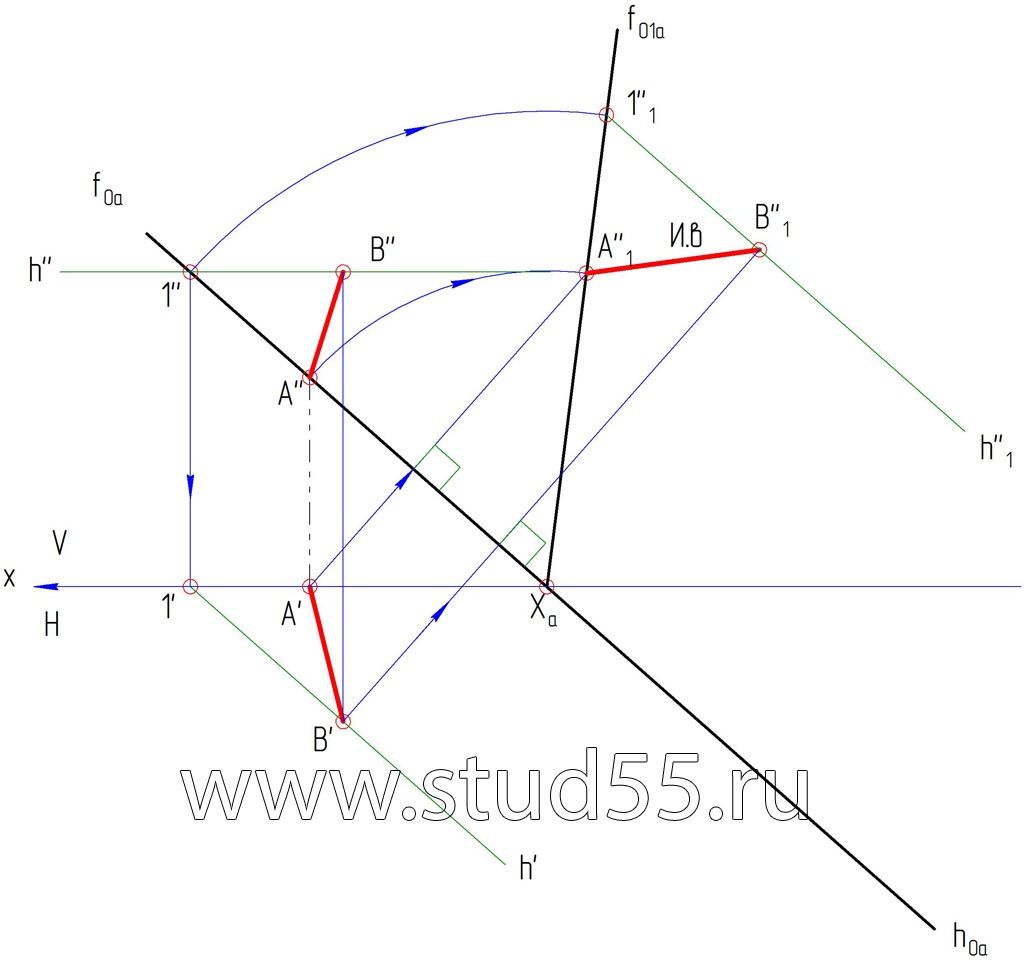
3) В совмещенной плоскости достраиваем искомую фигуру (квадрат со стороной АВ).

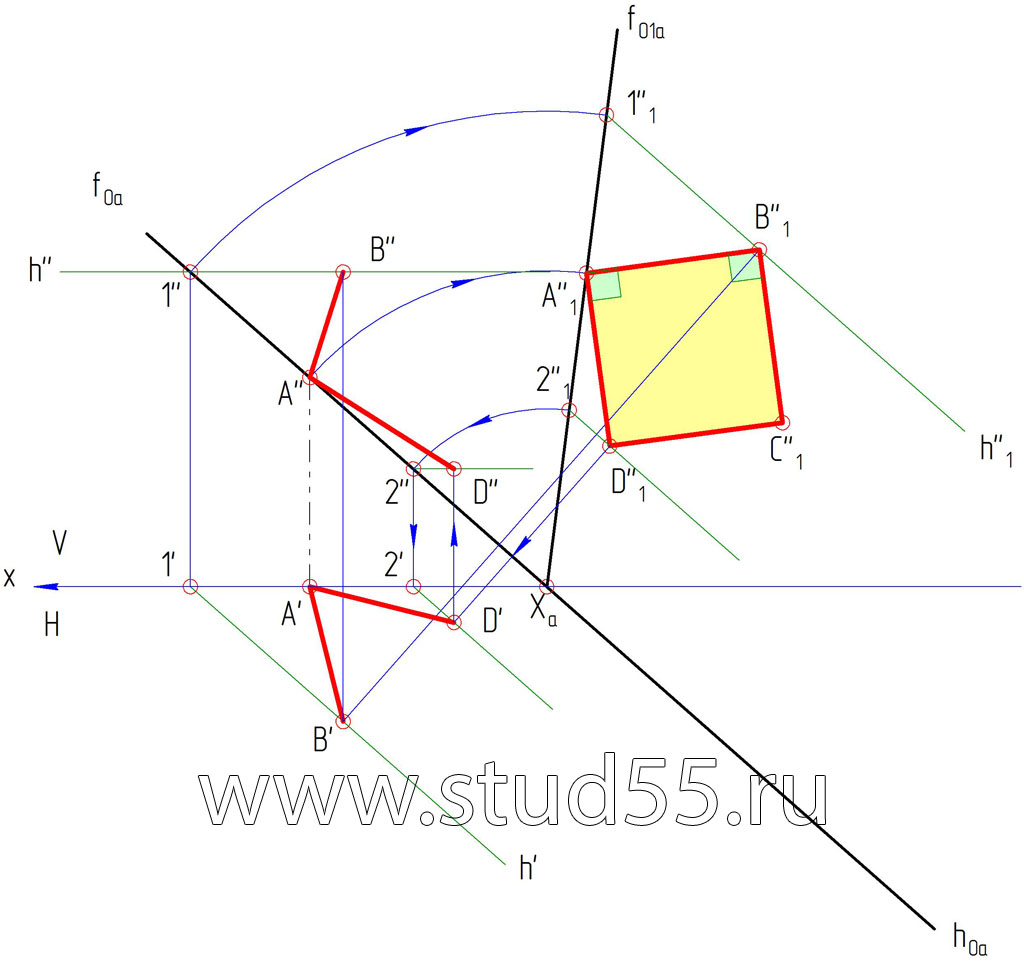
4) В совмещенной плоскости проводим горизонталь через проекцию точки D ( D»1), обратным вращением при помощи точки 2, находим горизонталь в плоскостяи проекций V, затем в H, а также проекции точки D — D’, затем по линии связи — D».

5) Проекции точки С (С» и C’) можно найти аналогичным способом, также как и нахождение точки D, или простыми построениями параллелограммов (квадрат отображается в виде параллелограмма).

У кого есть вопросы, пишите в комментариях!

Видео:Натуральная величина треугольника (метод вращения)Скачать

Натуральная величина треугольника

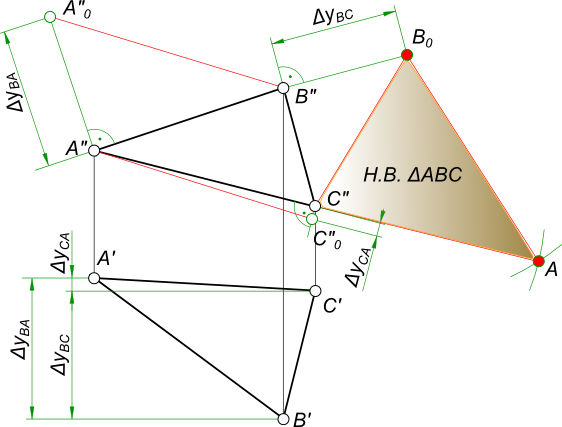
Натуральная величина треугольника на эпюре Монжа может быть определена: — способом прямоугольного треугольника;

Здесь поочередно применяется способ прямоугольного треугольника для определения действительных величин отрезков, составляющих треугольник, а затем, к одному из них методом засечек строятся два других.

Используем Метод преобразования проекций для определения истиной величины треугольника на эпюре Монжа:

— Способ вращения вокруг осей перпендикулярных плоскостям проекций;

— Вращение вокруг горизонтали представляющих собой линии уровня;

представляющих собой линии уровня;

— Вращение вокруг следа или способ совмещения с плоскостью проекций;

Задача на определение натуральной величины плоской фигуры относится к разделу метрические задачи.

🌟 Видео

Определение истинной величины треугольника АВС. Метод плоско-параллельного перемещенияСкачать

Способ замены (перемены) плоскостей проекции. Определение истинной величины отрезка и плоской фигурыСкачать

Построение натуральной величины треугольника методом вращенияСкачать

Способ вращения. Определение истинной величины отрезка.Скачать

Нахождение натуральной величины треугольника. Метод замены плоскостей проекцийСкачать

Определение натуральной величины треугольника АВD методом замены плоскостей проекции.Скачать

Определение длины отрезкаСкачать

Определение истинной величины двугранного угла АВСD при ребре АВ методом замены плоскостей проекцииСкачать

Задача №1 Определение натуральной величины отрезка прямой (АВ) методом прямоугольного треугольникаСкачать

Начерталка - Определение натуральной величины треугольника АВССкачать

Нахождение натуральной величины отрезка методом прямоугольного треугольникаСкачать

Построение натуральной величины треугольника АВС методом триангуляцииСкачать

Определить натуральную величину основания ABC методом вращения вокруг горизонтали или фронтали.Скачать

Натуральная величина отрезкаСкачать

Определение натуральной величины треугольника способом плоскопараллельного перемещения #решениезадачСкачать

Лекция 1. Точка на прямой. Метод прямоугольного треугольникаСкачать