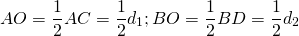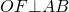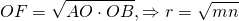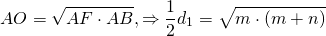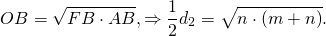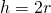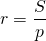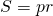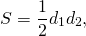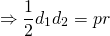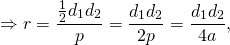В параллелограмм вписана окружность.
а) Докажите, что этот параллелограмм — ромб.
б) Окружность, касающаяся стороны ромба, делит её на отрезки, равные 5 и 3. Найдите площадь четырёхугольника с вершинами в точках касания окружности со сторонами ромба.
Пусть это параллелограмм ABCD, а точки касания со сторонами AB, BC, CD, DA обозначены за E, F, G, H соответственно.
а) Из описанности ABCD следует, что AB + CD = AD + BC, то есть 2AB = 2AD, значит, все стороны параллелограмма равны и это ромб.
б) Будем считать, что AE = 3, EB = 5. Центром окружности будет точка пересечения диагоналей ромба O, а радиус этой окружности — высота прямоугольного треугольника Тогда по теореме Пифагора находим
Значит,
Поскольку точки E и F делят стороны AB и BC в одинаковом отношении 3 : 5, треугольники BEF и BAC подобны с коэффициентом и
Рассматривая аналогично остальные стороны EFGH, получаем, что это параллелограмм и даже прямоугольник (так как
). Значит, его площадь равна:
Ответ:
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Имеется верное доказательство утверждения пункта a и обоснованно получен верный ответ в пункте б | 3 |
| Получен обоснованный ответ в пункте б имеется верное доказательство утверждения пункта а и при обоснованном решении пункта б получен неверный ответ из-за арифметической ошибки | 2 |
| Имеется верное доказательство утверждения пункта а при обоснованном решении пункта б получен неверный ответ из-за арифметической ошибки, Содержание Видео:Геометрия В треугольник ABC вписана окружность радиуса R, касающаяся стороны AC в точке D, причёмСкачать  Узнать ещёЗнание — сила. Познавательная информация Видео:№700. Докажите, что в любой ромб можно вписать окружность.Скачать  В ромб вписана окружностьКогда в условии задачи сказано, что в ромб вписана окружность, в ходе ее решения может быть использовано одно из следующих рассуждений. В этом случае радиус ромба и его диагонали можно найти, используя соотношения в прямоугольном треугольнике. Например, F — точка касания вписанной в ромб окружности — делит сторону AB на отрезки AF=m, FB=n. О — центр вписанной в ромб окружности — является точкой пересечения его диагоналей. Треугольник AOB — прямоугольный (так как диагонали ромба взаимно перпендикулярны). — как радиус, проведенный в точку касания. Значит, OF — высота, проведенная к гипотенузе. Отсюда Высота ромба через радиус вписанной окружности Радиус вписанной в ромб окружности Радиус вписанной окружности можно найти по формуле S — площадь ромба, p — его полупериметр (p=2a, где a — сторона ромба). Соответственно, площадь ромба через радиус вписанной в него окружности Поскольку площадь ромба также равна Площадь ромба через отрезки, на которые делит сторону ромба точка касания вписанной в него окружности, может быть найдена как Видео:Касательные к окружности с центром O в точках A и B ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать  Вариант Ларина №367 ЕГЭ 2022 по математике профиль с ответамиПОДЕЛИТЬСЯТренировочный вариант №367 Алекса Ларина ЕГЭ 2022 по математике профильный уровень 11 класс с ответами и решением по новой демоверсии ЕГЭ 2022 года для подготовки к экзамену, дата выхода варианта: 06.11.2021 (6 ноября 2021 года) Скачать вариант ЛаринаОтветы для вариантаЭкзаменационная работа состоит из двух частей, включающих в себя 18 заданий. Часть 1 содержит 11 заданий с кратким ответом базового и повышенного уровней сложности. Часть 2 cодержит 7 заданий с развёрнутым ответом повышенного и высокого уровней сложности. Решать вариант Алекса Ларина №367 ЕГЭ 2022 по математике:Сложные задания и ответы с варианта:2)В группе шесть человек, среди них – Михаил и Олег. Группу случайным образом делят на 3 пары. Найти вероятность того, что Михаил и Олег окажутся в одной паре. Ответ: 0,2 3)В ромб ABCD вписана окружность, касающаяся стороны AD в точке F. Известно, что AF =4 ∙ FD. Найдите косинус острого угла ромба. Ответ: 0,6 5)На рисунке изображен многогранник, все двугранные углы которого прямые. Найдите квадрат расстояния между вершинами А и С3. Ответ: 17 6)На рисунке изображен график функции . На оси абсцисс отмечены точки ‐2, ‐1, 1, 4. В какой из этих точек значение производной наименьшее? В ответе укажите эту точку. Ответ: 4 8)Из пункта А в пункт В вышел грибник, через час из А в В вышел турист, скорость которого на 25% больше скорости грибника, а еще через час после этого из А в В вышел спортсмен, скорость которого на 60% больше скорости туриста. Грибник и турист прибыли в пункт В одновременно. На сколько минут раньше прибыл в пункт В спортсмен? Ответ: 30 10)Турнир по настольному теннису проводится по олимпийской системе: игроки случайным образом разбиваются на игровые пары; проигравший в каждой паре выбывает из турнира, а победитель выходит в следующий тур, где встречается со следующим противником, который определен жребием. Всего в турнире 16 игроков, все они играют одинаково хорошо, поэтому в каждой встрече вероятность выигрыша и поражения у каждого игрока равна 0,5. Среди игроков два друга – Иван и Алексей. Какова вероятность того, что этим двоим в каком‐то туре придется сыграть друг с другом? Ответ: 0,125 13)В кубе ABCDA1B1C1D1 ребро которого равно 3, проведено сечение через вершину В и середины ребер A1D1 и C1D1. А) Найдите угол между плоскостью сечения и плоскостью BCC1 Б) Найдите объем пирамиды, основанием которой является сечение куба, а вершиной – точка D. 15)Трейдер потратил треть своих денег на приобретение акций одного АО, а остальные деньги ‐ на акции второго АО. Спустя три месяца цены акций обоих АО выросли на определенные для каждого АО проценты, а еще через три месяца цены акций выросли на столько же процентов, что и в предыдущий период. В результате за полгода общая стоимость акций трейдера выросла на 98%. Если бы после первых трех месяцев трейдер продал все акции первого АО по новой цене и на все полученные деньги приобрел бы акции второго АО, то общий прирост инвестиций за полгода составил бы 110%. Какой процент прибыли получит трейдер за полгода, вложив всю сумму в акции первого АО? Ответ: 44 18)А) Приведите пример четырёхзначного числа, произведение цифр которого в 10 раз больше суммы цифр этого числа. Б) Существует ли такое четырёхзначное число, произведение цифр которого в 175 раз больше суммы цифр этого числа? В) Найдите все четырёхзначные числа, произведение цифр которых в 50 раз больше суммы цифр этого числа. 🔥 Видео11.46.1. Планиметрия. Гордин Р.К.Скачать  Вписанные и описанные четырехугольники. Практическая часть. 9 класс.Скачать  Урок 2. Описанная окружность около четырехугольника. Задача из ОГЭ| Подобные треугольникиСкачать  Вписанная и описанная окружность - от bezbotvyСкачать  🔴 В угол C, равный 165°, вписана окружность с ... | ЕГЭ БАЗА 2018 | ЗАДАНИЕ 15 | ШКОЛА ПИФАГОРАСкачать  ЕГЭ Математика Задание 6#27935Скачать  Задача 6 №27913 ЕГЭ по математике. Урок 131Скачать  ОГЭ Задание 25 Окружность вписанная в прямоугольный треугольникСкачать  №1035. В окружности проведены хорды АВ и CD, пересекающиеся в точке Е. Найдите острыйСкачать  ЕГЭ задание 16Скачать  Один отрезок - диагональ четырёхугольника, диаметр окружности, высота ромбаСкачать  Точка E середина стороны AD параллелограмма ABCDСкачать  Вписанные и описанные окружности. Вебинар | МатематикаСкачать  Всё про углы в окружности. Геометрия | МатематикаСкачать  Окружность вписанная в треугольник и описанная около треугольника.Скачать  Окружность вписана в равнобедренный треугольник. Найти её радиус.Скачать  Подготовка к ЕГЭ, ОГЭ. Геометрия. Параллелограмм, ромб, квадрат, площади. Вписанная окружность.СинусСкачать  |
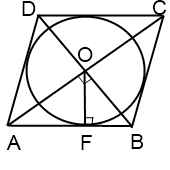 Точка касания вписанной в ромб окружности делит его сторону на отрезки
Точка касания вписанной в ромб окружности делит его сторону на отрезки