На окружности отмечено 8 точек сколько различных выпуклых четырехугольников

Видео:Как решить любую задачу с четырёхугольниками? | Математика TutorOnlineСкачать

Контрольная работа по алгебре и началам анализа для 11 класса по теме » Комбинаторика»
методическая разработка по алгебре (11 класс) на тему

Контрольная работа по алгебре и началам анализа для 11 класса по теме » Комбинаторика»

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Скачать:

Бесплатный марафон подготовки к ЕГЭ на зимних каникулах

Учи.Дома запускает бесплатный марафон в котором каждый день. В течении 5 дней утром ты будешь получать одно задание по выбранному предмету, а вечером его решение. Твоя задача, успеть выполнение задание до того как получишь ответ.

Бесплатно, онлайн, подготовка к ЕГЭ

Видео:§63 Сочетания и их свойстваСкачать

Предварительный просмотр:

Контрольная работа по алгебре по теме «Комбинаторика»

3.Найти значение выражения:

4. Решить уравнение:

5. На окружности отмечено 7 точек. Сколько различных выпуклых четырёхугольников с вершинами, выбранными из этих точек, можно построить?

6. Записать разложение бинома:

Видео:Сумма внутренних углов многоугольника. Выпуклые и невыпуклые многоугольники. 8 класс.Скачать

Предварительный просмотр:

Контрольная работа по алгебре по теме «Комбинаторика»

3.Найти значение выражения:

4. Решить уравнение:

5. На окружности отмечено 8 точек. Сколько различных выпуклых четырёхугольников с вершинами, выбранными из этих точек, можно построить?

6. Записать разложение бинома:

Видео:8 класс, 3 урок, ЧетырехугольникСкачать

По теме: методические разработки, презентации и конспекты

Рейтинговые контрольные работы по алгебре и началам анализа. 10 класс. УМК Ю.М.Колягина и др.

Комплект контрольных работ по алгебре и началам анализа. 10 класс.

Контрольные работы по алгебре и началам анализа. 10 класс.

При составлении работ учитывалась необходимость дифференциального подхода к обучению. Все работы состоят из трех уровней: А, В и С. Уровень А, называемый уровнем воспроизведения, предусматривает знани.

Административная контрольная работа по алгебре и началам анализа 10 класс

Административная контрольная работа по алгебре и началам анализа 10 класс за первое полугодие учебного года.

Входная контрольная работа по алгебре и началам анализа, 10 класс

Входная контрольная работа по алгебре и началам анализа, 10 класс.

Видео:МЕРЗЛЯК-8 ГЕОМЕТРИЯ. ОПИСАННАЯ И ВПИСАННАЯ ОКРУЖНОСТИ ЧЕТЫРЁХУГОЛЬНИКА. ПАРАГРАФ-10. ТЕОРИЯСкачать

На окружности отмечено 8 точек сколько различных выпуклых четырехугольников с вершинами выбранными

Задача 1: (5–7) Бывают ли натуральные числа, произведение цифр которых равно 1986,?

Решение: Воспользуемся тем, что если произведение нескольких чисел делится на простое число, то хотя бы один из сомножителей делится на это число. Это утверждение следует из теоремы о единственности разложения на простые множители (см. также свойство 4 из Т4). Поэтому из того, что произведение цифр числа равно 1986, и что число 1986 делится на 331, следует, что одна из этих цифр делится на 331. Это, очевидно, невозможно.

Задача 2: (5–7) Найти две обыкновенные дроби — одну со знаменателем 8, другую со знаменателем 13 такие, чтобы они не были равны, но разность между большей и меньшей из них была как можно меньше.

Решение: Пусть первая дробь равна ,, а вторая — ,. Тогда разность между большей и меньшей из них равна ,. В числителе полученной дроби стоит целое положительное число. Поэтому она не может быть меньше ,. А быть равной — может. Для этого нужно, чтобы числитель был равен единице. Это выполняется, если, например, x = 3, y = 5 (или x = 5, y = 8).

Задача 3: (5–7) За круглым столом сидело а) 15; б) 20 человек. Они хотят пересесть так, чтобы те, кто раньше сидел рядом, теперь сидели бы через два человека. Возможно ли это?

Решение: а) Пронумеруем все места за столом по кругу и всех сидящих соответственно занимаемым местам. Будем считать, что нам удалось всех пересадить требуемым образом. Без ограничения общности можно считать, что человек 1 остался сидеть на своем месте. Если это не так, то этого можно добиться поворотом стола; при этом условие задачи нарушиться, очевидно, не может. Человек 2 может сидеть либо на месте 4, либо на месте 13. Разберем первый из этих случаев (рис. 15 a). В этом случае для третьего есть единственное место, удовлетворяющее условию — 7. Далее, 4-й может сидеть только на месте 10, 5-й — на месте 13. При этом для 6-го единственное возможное место — 1. Но оно уже занято первым. Значит, рассадить людей требуемым образом не удастся. Второй случай разбирается аналогично.

б) Опять пронумеруем места подряд вокруг стола и людей соответственно занимаемым местам. На рис. 15 б) показан способ пересадить людей, удовлетворяющий условиям задачи.

Задача 4: (8–9) В компании из k человек (k > 3) у каждого появилась новость, известная ему одному. За один телефонный разговор двое сообщают друг другу все известные им новости. Докажите, что за 2k – 4 разговора все они могут узнать все новости.

Решение: Передача информации может быть осуществлена следующим образом. Рассмотрим некоторых четверых людей в компании — назовем их A, B, C, D. Пусть сначала все члены компании, кроме B, C и D звонят A и сообщают ему свои новости. Это потребует k – 4 звонка. Затем между собой говорят A и B, а также C и D. После этого A говорит с C, а B с D, в результате чего все четверо будут знать все новости. За оставшиеся 2n – 4 звонка A сообщает их всем остальным.

Задача 5: (8–9) Через данную точку на плоскости проводятся всевозможные прямые, пересекающие данную окружность. Найти геометрическое место середин получившихся хорд.

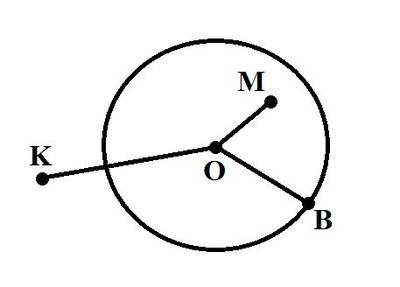
Решение: Искомое геометрическое место середин хорд — это дуга окружности, построенной на отрезке, соединяющем данную точку и центр данной окружности, как на диаметре, лежащая внутри данной окружности (в частности, если точка лежит внутри окружности, то получается вся окружность).

Пусть O — центр данной окружности, M — данная точка, l — произвольная прямая, пересекающая окружность и проходящая через точку M, H — середина хорды, получающейся при пересечении прямой окружности (рис. 16). Воспользуемся известной теоремой: радиус перпендикулярен хорде тогда и только тогда, когда он делит ее пополам. Из этой теоремы следует, что угол MHO — прямой. Из обратной теоремы о величине угла, опирающегося на диаметр, следует, что точка H лежит на окружности с диаметром OM. Обратно, пусть H — точка, лежащая на окружности с диаметром OM и внутри данной окружности. По прямой теореме о величине угла, опирающегося на диаметр, получаем, что прямые MH и HO перпендикулярны. Применив теорему о радиусе, перпендикулярном хорде, еще раз, получим, что k — середина хорды, образованной прямой, проходящей через точку M.

Задача 6: (8–9) Известно, что a + b + c = 5 и ab + bc + ac = 5. Чему может равняться a² + b² + c²,?

Решение: Воспользуемся формулой (a + b + c)² = a² + b² + c² + 2ab + 2bc + 2ac. Имеем a² + b² + c² = (a + b + c)² – 2(ab + bc + ac) = 5² – 2 • 5 = 15.

Задача 7: (8–9) На плоскости отмечено 5 точек с целыми координатами. Докажите, что середина по крайней мере одного из соединяющих их отрезков также имеет целые координаты.

Решение: Воспользуемся тем, что координаты середины отрезка с концами (x ₁ ,y ₁ ) и (x ₂ ,y ₂ ) равны (докажите это). Среди пяти точек с целыми координатами найдутся три, абсциссы которых имеют одинаковую четность (то есть либо все четны, либо все нечетны). Действительно, если бы точек с четными абсциссами было не больше двух и с нечетными абсциссами не больше двух, то всего точек было бы не больше четырех. Аналогично, среди этих трех точек найдутся две с ординатами одной четности. Пусть это точки (x ₁ ,y ₁ ) и (x ₂ ,y ₂ ). Поскольку x ₁ и x ₂ либо оба четны, либо оба нечетны, то x ₁ + x ₂ — четное, и — целое. Аналогично, — целое. Утверждение доказано.

Задача 8: (5–7) Вершины выпуклого пятиугольника соединены через одну. Найдите сумму углов при вершинах получившейся звезды.

Решение:

Пусть ABCDE исходный пятиугольник, а A′B′C′D′E′ — пятиугольник, образованный при пересечении его диагоналей (рис. 17). Рассмотрим сумму углов пяти треугольников ACB′, BDC′, CED′, DAE′ и EBA′. В эту сумму входят по два раза углы звезды ACEBD и по разу углы пятиугольника A′B′C′D′E′. Поскольку сумма углов любого треугольника равна 180, а пятиугольника — 540. Отсюда выводим, что искомая сумма углов равна 180.

Задача 9: (5–7) Верно ли, что из любых 10 отрезков найдутся три, из которых можно составить треугольник?

Решение:

Рассмотрим 10 отрезков с длинами 1, 2, 4, …, 512 (каждый следующий вдвое длиннее предыдущего). Тогда пусть a, b и c — длины любых трех из данных отрезков, причем a 1 , a ₂ , a ₃ , a ₄ , a ₅ , a ₆ — последовательные стороны шестиугольника, все углы которого равны. Докажите, что a ₁ – a ₄ = a ₃ – a ₆ = a ₅ – a ₂ .

Решение:

Продолжим стороны данного шестиугольника ABCDEF до пересечения друг с другом. Шестиугольник оказался представленным в виде пересечения двух равносторонних треугольников KMO и LNP (рис. 20) со сторонами b и c соответственно. Объединение этих треугольников представляет собой шестиконечную звезду, лу-чи которой ABK, BCL, CDM, DEN, EFO и FAP являются равносторонними треугольниками. Можем записать

Аналогично получаем, b – c = a ₃ – a ₆ и b – c = a ₅ – a ₂ , откуда следует требуемое равенство.

Задача 14: (8–9) «Крокодилом» называется фигура, ход которой заключается в прыжке на клетку, в которую можно попасть сдвигом на одну клетку по вертикали или горизонтали, а затем на N клеток в перпендикулярном направлении (при N = 2 «крокодил» — это шахматный конь). При каких N «крокодил» может пройти с любой клетки бесконечной шахматной доски на любую другую?

Решение:

Будем считать, что рассматриваемая бесконечная шахматная доска, как и обычная, раскрашена в белый и черный цвета в шахматном порядке. Тогда при нечетном N «крокодил» будет ходить только по клеткам одного цвета, и, тем самым не может пройти на любую клетку.

Докажем теперь, что при четном N «крокодил» может пройти с любой клетки на любую. Очевидно, для этого достаточно доказать, что он может пройти с любой клетки на соседнюю (смежную по стороне). Покажем, как пройти из клетки в соседнюю с ней сверху. Первым ходом ходим на одну клетку вправо и N клеток вверх, а вторым — на одну вправо и N вниз. Так мы окажемся на две клетки правее исходной. Повторим эту пару ходов N/2 раз (тогда мы окажемся на N клеток правее исходной), после чего пойдем на одну клетку вверх и N влево. Мы оказались в клетке, соседней с исходной.

Задача 15: (8–9) Фабрика окрашивает кубики в 6 цветов (каждую грань в свой цвет, набор цветов фиксирован). Сколько разновидностей кубиков можно изготовить?

Решение:

Предположим, что процедура раскраски кубика происходит следующим образом: непокрашенный кубик устанавливается в станок в некоторое фиксированное положение, а затем последовательно красятся его грани в определенном порядке: нижняя, верхняя, правая, левая, передняя, задняя. Посчитаем сначала, сколькими способами можно осуществить такую раскраску. Нижнюю грань мы можем покрасить любой из шести красок. После этого для верхней грани останется лишь пять возможностей, поскольку одна краска уже использована. Затем правую грань мы сможем покрасить четырьмя способами, левую — тремя, переднюю двумя, а выбора для цвета задней грани нет — ее мы вынуждены покрасить в оставшийся неиспользованным цвет. Поэтому всего способов раскраски 6 • 5 • 4 • 3 • 2 = 720. Однако же, получающихся разновидностей кубиков гораздо меньше, поскольку установить кубик в фиксированное положение можно различными способами. Сколькими? Кубик можно установить на любую из шести граней и затем повернуть одним из четырех способов — получаем всего 6 • 4 = 24 способа. Поэтому разновидностей кубиков в 24 раза меньше, чем способов раскраски, их всего 30.

Задача 16: (8–9) Докажите, что произведение ста последовательных натуральных чисел не может быть сотой степенью натурального числа.

Решение:

Предположим, что для некоторых натуральных n и k

Тогда n 1 и S ₂ соответственно (рис. 23,б). Площадь треугольника не меньше половины произведения двух его сторон. Это следует из того, что сторона треугольника не меньше высоты, опущенной на другую сторону. Сложив неравенства и , получим требуемое неравенство.

Пусть теперь стороны a и b четырехугольника несмежны. Разобьем снова данный четырехугольник на два треугольника диагональю. Теперь треугольник, имеющий стороны a и d оставим на месте, а имеющий стороны b и c отразим относительно серединного перпендикуляра к проведенной диагонали (рис. 23,в). Получим четырехугольник той же площади, с теми же сторонами, но идущими в другом порядке (стороны a и b, а также c и d в нем смежны). Для такого четырехугольника неравенство нами уже доказано. А из этого и следует неравенство для рассматриваемого исходного четырехугольника.

Видео:Вписанные и описанные окружности. Вебинар | МатематикаСкачать

Контрольная работа по алгебре и началам анализа для 11 класса по теме » Комбинаторика»
методическая разработка по алгебре (11 класс) на тему

Контрольная работа по алгебре и началам анализа для 11 класса по теме » Комбинаторика»

Видео:Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

Скачать:

Видео:ЩЕЛЧОК ОГЭ по математике | Вся теория по окружности. Решение №16,23Скачать

Предварительный просмотр:

Контрольная работа по алгебре по теме «Комбинаторика»

3.Найти значение выражения:

4. Решить уравнение:

5. На окружности отмечено 7 точек. Сколько различных выпуклых четырёхугольников с вершинами, выбранными из этих точек, можно построить?

6. Записать разложение бинома:

Видео:🔴 На окружности отмечена точка C. Отрезок AB ... | ЕГЭ БАЗА 2018 | ЗАДАНИЕ 15 | ШКОЛА ПИФАГОРАСкачать

Предварительный просмотр:

Контрольная работа по алгебре по теме «Комбинаторика»

3.Найти значение выражения:

4. Решить уравнение:

5. На окружности отмечено 8 точек. Сколько различных выпуклых четырёхугольников с вершинами, выбранными из этих точек, можно построить?

6. Записать разложение бинома:

Видео:Повторение изученного в 8 классе Геометрия все темы просто! Вся геометрия 8 в одном уроке. ВидеоурокСкачать

По теме: методические разработки, презентации и конспекты

Рейтинговые контрольные работы по алгебре и началам анализа. 10 класс. УМК Ю.М.Колягина и др.

Комплект контрольных работ по алгебре и началам анализа. 10 класс.

Контрольные работы по алгебре и началам анализа. 10 класс.

При составлении работ учитывалась необходимость дифференциального подхода к обучению. Все работы состоят из трех уровней: А, В и С. Уровень А, называемый уровнем воспроизведения, предусматривает знани.

Административная контрольная работа по алгебре и началам анализа 10 класс

Административная контрольная работа по алгебре и началам анализа 10 класс за первое полугодие учебного года.

Входная контрольная работа по алгебре и началам анализа, 10 класс

Входная контрольная работа по алгебре и началам анализа, 10 класс.

Видео:Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать

ГДЗ по математике 2 класс учебник Рудницкая, Юдачева часть 1 Страница 99-106

Страница 99

1. Сколько на столе пирожных?
Как решил задачу Волк и как — Заяц? Кто из них быстрее справился с задачей? Почему?
Ответ:
Волк решил так:
1. сложил пирожные на первой тарелке с пирожными на второй тарелке.
2. сумму пирожных на двух тарелках сложил с пирожными на третьей тарелке.
3. сумму пирожных на трех тарелках сложил с пирожными на четвертой тарелке.
4. сумму пирожных на четырех тарелках сложил с пирожными на пятой тарелке.
5. сумму пирожных на пяти тарелках сложил с пирожными на шестой тарелке.
6. сумму пирожных на шести тарелках сложил с пирожными на седьмой тарелке.
7. сумму пирожных на семи тарелках сложил с пирожными на восьмой тарелке
2 + 2 = 4 пирожных — на двух тарелках
4 + 2 = 6 пирожных — на трех тарелках
6 + 2 = 8 пирожных — на четырех тарелках
8 + 2 = 10 пирожных — на пяти тарелках
10 + 2 = 12 пирожных — на шести тарелках
12 + 2 = 14 пирожных — на семи тарелках
14 + 2 = 16 пирожных — на восьми тарелках
Заяц умножил количество пирожных на одной тарелке на количество тарелок.
2 • 8 = 16 пирожных — на восьми тарелках
Поэтому Заяц справился с заданием быстрее, чем волк.

Страница 100

2. Объясни, как сделаны записи.
2 • 2 = 4 2 • 3 = 6 2 • 4 = 8
Ответ:
Количество фишек в одном ряду умножили на количество рядов:
На 1 рисунке: 2 фишки в одном ряду умножили на 2 ряда получили 4 фишки.
На 2 рисунке: 2 фишки в одну ряду умножили на 3 ряда получили 6 фишек.
На 3 рисунке: 2 фишки в одном ряду умножили на 4 ряда получили 8 фишек.

3. Сколько рядов с двумя фишками надо взять, чтобы умножить 2 на 0?
Сколько фишек должно быть в ряду, чтобы умножить 0 на 2? Какой результат получится, если взять это число фишек два раза?
Ответ:
Чтобы умножить 2 на 0, нужно взять 0 рядов по 2 фишки (2 • 0 = 0).
Чтобы умножить 0 на 2, должно быть 2 ряда по 0 фишек (0 • 2 = 0).
Если взять 0 фишек два раза, то получится 0 (0 • 0 = 0).

4. Найди результаты умножения.
2 • 5 2 • 8
2 • 6 2 • 9
2 • 7 2 • 4
Ответ:
2 • 5 = 10
2 • 6 = 12
2 • 7 = 14
2 • 8 = 16
2 • 9 = 18
2 • 4 = 8

5. Сравни результаты умножения, используя калькулятор.
2 • 6 и 6 • 2 3 • 2 и 2 • 3
9 • 2 и 2 • 9 2 • 1 и 1 • 2
Сделай вывод.
Ответ:
2 • 6 = 12 6 • 2 = 12
9 • 2 = 18 2 • 9 = 18
3 • 2 = 6 2 • 3 = 6
2 • 1 = 2 1 • 2 = 2
Можно сделать вывод, что от перемены мест множителей произведение не меняется.

6. Используя таблицу умножения числа 2, составь и запиши таблицу умножения на число 2.
Ответ:
2 • 1 = 2
2 • 2 = 4
2 • 3 = 6
2 • 4 = 8
2 • 5 = 10
2 • 6 = 12
2 • 7 = 14
2 • 8 = 16
2 • 9 = 18
2 • 10 = 20

7. Назови результаты умножения.
6 • 2 4 • 2 7 • 2 9 • 2
8 • 2 3 • 2 1 • 2 5 • 2
Ответ:
6 • 2 = 12
8 • 2 = 16
4 • 2 = 8
3 • 2 = 6
7 • 2 = 14
1 • 2 = 2
9 • 2 = 18
5 • 2 = 10

Страница 101

8. В каждый из 6 кувшинов налили 2 стакана молока. Сколько молока в этих кувшинах?
Ответ:
6 • 2 = 12 стаканов — молока в 6 кувшинах

9. На каждую из 8 тарелок положили 2 куска торта. Сколько кусков торта на этих тарелках?
Ответ:
8 • 2 = 16 кусков — торта на 8 тарелках

10. Из бочки, в которой было 40 л воды, взяли 2 раза по 9 л. Сколько литров воды осталось?
Ответ:
1) 2 • 9 = 18 литров — воды взяли из бочки
2) 40 — 18 = 22 литра — воды осталось

11. Пять цыплят склевали по 2 червяка, а шестой — 3 червяка. Сколько червяков склевали цыплята?
Ответ:
1) 5 • 2 = 10 червяков — склевали 5 цыплят
2) 10 + 3 = 13 червяков — склевали 6 цыплят

12. На сколько квадратов разделён каждый четырёхугольник? Посчитай разными способами.
Ответ:
Желтый четырехугольник.
1 способ: 1 + 1 + 1 + 1 + 1 + 1 = 6 квадратов
2 способ: 2 + 2 + 2 = 6 квадратов
3 способ: 3 + 3 = 6 квадратов
4 способ: 2 • 3 = 6 квадратов
5 способ: 3 • 2 = 6 квадратов

Зеленый четырехугольник.
1 способ: 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 = 18 квадратов
2 способ: 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 = 18 квадратов
3 способ: 9 + 9 = 18 квадратов
4 способ: 2 • 9 = 18 квадратов
5 способ: 9 • 2 = 18 квадратов

13. Используя таблицу умножения на 2, выполни деление.
6 : 2 14 : 2 4 : 2 12 : 2
10 : 2 16 : 2 8 : 2 18 : 2
Ответ:
6 : 2 = 3
10 : 2 = 5
14 : 2 = 7
16 : 2 = 8
4 : 2 = 2
8 : 2 = 4
12 : 2 = 6
18 : 2 = 9

Страница 102

14. Выполни действия.
6 • 2 2 • 8 7 • 2 9 • 2
12 : 2 16 : 2 14 : 2 18 : 2
Ответ:
6 • 2 = 12
12 : 2 = 6
2 • 8 = 16
16 : 2 = 8
7 • 2 = 14
14 : 2 = 7
9 • 2 = 18
18 : 2 = 9

15. Какое число получится, если умножить 0 на 2 и разделить результат на 2?
Ответ:
0 • 2 = 0 0 : 2 = 0

16. На 2 блюдца разложили поровну 6 слив. Сколько слив на каждом блюдце?
Ответ:
6 : 2 = 3 сливы — на каждом блюдце

17. Для бутербродов нарезали 8 ломтиков сыра. На один бутерброд кладут 2 ломтика. Хватит ли нарезанного сыра для приготовления шести бутербродов?
Ответ:
1) 8 : 2 = 4 бутерброда получится из 8 ломтиков сыра
2) 2 • 6 = 12 ломтиков — сыра нужно для 6 бутерброд
3) 12 — 8 = 4 ломтика — сыра не хватает
Следовательно, 8 ломтиков сыра не хватит для приготовления шести бутербродов.

18. Из данных задач выбери и реши только задачу на деление.
1) В столовой за один стол сели 4 ребёнка, а за другой — 2. Сколько всего детей село за два стола?
2) Четверо туристов расселись в лодки по 2 человека. Сколько лодок заняли туристы?
3) Четыре подружки съели по 2 плюшки. Сколько плюшек съели подружки?
Ответ:
Четверо туристов расселись в лодки по 2 человека. Сколько лодок заняли туристы?
4 : 2 = 2 лодки — заняли туристы

Страница 103

19. У Коли 10 марок. Половину этих марок он подарил Пете. Сколько марок Коля подарил Пете?
Ответ:
10 : 2 = 5 марок — Коля подарил Пете

20. На прогулку вывели 10 собак. Половина этих собак — овчарки, а остальные — пудели. Сколько вывели пуделей?
Ответ:
1) 10 : 2 = 5 собак — овчарки
2) 10 — 5 = 5 собак — пудели

21. Половина цветов в букете — колокольчики, остальные 7 — ромашки. Сколько цветов в букете?
Ответ:
Если колокольчики составляют половину букета, а остальные — ромашки. То колокольчиков такое же количество как и ромашек — 7.
7 + 7 = 14 цветов — в букете
или 7 • 2 = 14 цветов — в букете

22. В сквере растут липы и каштаны. Липы составляют половину всех деревьев. Сколько в сквере деревьев, если лип 9?
Ответ:
Если липы составляют половину всех деревьев, то каштаны составляют вторую половину деревьев. Значит, каштанов такое же количество как и лип — 9.
9 + 9 = 18 — деревьев в сквере
или 9 • 2 = 18 — деревьев в сквере

23. Назови результаты действий.
6 + 4 15 — 9 12 — 7 4 + 5
11 — 5 3 + 8 9 + 2 11 — 5
8 + 7 18 — 9 14 — 8 9 + 0
13 — 4 5 + 6 7 + 7 12 — 8
Ответ:
6 + 4 = 10 15 — 9 = 6 12 — 7 = 4 4 + 5 = 9
11 — 5 = 6 3 + 8 = 11 9 + 2 = 11 11 — 5 = 6
8 + 7 = 15 18 — 9 = 9 14 — 8 = 6 9 + 0 = 9
13 — 4 = 9 5 + 6 = 11 7 + 7 = 14 12 — 8 = 4

Страница 104

24. Вычисли.
(45 + 38) — 54
96 — (63 — 36)
(100 — 67) + 15
74 + (8 + 18)
Ответ:
(45 + 38) — 54 = 83 — 54 = 29
96 — (63 — 36) = 96 — 27 = 69
(100 — 67) + 15 = 33 + 15 = 48
74 + (8 + 18) = 74 + 26 = 100

25. Катя хочет надеть на куклу блузку и юбку. Сколько разных костюмов она может составить, если имеется 2 юбки и 3 блузки?
Действуй по плану.
1) Выбери одну из двух юбок и присоединяй к ней по порядку каждую из трёх блузок.
2) Ко второй юбке присоединяй по порядку каждую из трёх блузок.
Проверь своё решение: всего должно получиться 6 костюмов.
Ответ:
1) Юбка в складку и бело-зеленая блузка, юбка в складку и белая в розовую полоску блузка, юбка в складку и желтая с цветами блузка.
2) Джинсовая юбка и бело-зеленая блузка, джинсовая юбка и белая в розовую полоску блузка, ​​​​​​​джинсовая юбка и желтая с цветами блузка.
Да, всего получится 6 костюмов.

26. Начерти два отрезка так, чтобы их общей частью была точка. Рассмотри разные варианты расположения отрезков.
Ответ:

27. Начерти окружность и луч так, чтобы луч пересекал эту окружность в одной точке; в двух точках.
Ответ:

Страница 105.

28. Миша говорит, что он начертил отрезки, симметричные относительно оси. Верно ли Миша выполнил чертёж?
Ответ:
Если перегнуть лист по оси (красной линии), то отрезки должны совпасть. В данном случае отрезки не совпадут, а будут параллельны друг другу. Поэтому Миша выполнил чертеж не верно.

29. Начерти какую-нибудь окружность с центром в точке О. Отметь три точки: точку К — вне окружности, точку В — на окружности и точку М — внутри окружности. Построй отрезки ОК, ОВ и ОМ. Не производя измерений, сравни длины отрезков ОК и ОВ, ОК и ОМ, ОВ и ОМ. Свои ответы поясни.
Ответ:

Отрезок OB находится на окружности, т.е. является ее радиусом, а отрезок OK находится за пределами окружности, поэтому ОК>ОВ
Отрезок OK находится за пределами окружности, а отрезок OM внутри окружности, поэтому ОК>ОМ
Отрезок OB равен радиусу, а отрезок OM внутри окружности, т.е. меньше радиуса, поэтому ОВ>ОМ

30. Найди неизвестные числа.
Число 42 меньше неизвестного числа на 19. Чему равно неизвестное число?
Число 63 больше неизвестного числа на 24. Чему равно неизвестное число?
Коля задумал двузначное число. В нём 10 десятков без 9 единиц. Какое это число?
Ответ:
Число 42 меньше неизвестного числа на 19. Чему равно неизвестное число?

Число 63 больше неизвестного числа на 24. Чему равно неизвестное число?

​​​​​​​
Коля задумал двузначное число. В нём 10 десятков без 9 единиц. Какое это число?
10 десятков = 100
9 единиц = 9
А 10 десятков без 9 единиц, т.е. надо из 100 вычесть 9

31. Выполни действия.
57 + 20 60 + 30 38 — 22
67 — 9 27 + 17 100 — 23
35 + 27 72 — 7 46 + 48
83 — 40 83 — 21 54 + 39
Ответ:

32. У Маши 40 рублей, а у Кати на 16 рублей больше. Девочки купили на все деньги одну игрушку. Какова её цена?
Ответ:
1) 40 + 16 = 56 рублей — у Кати
2) 40 + 56 = 96 рублей — цена игрушки

Страница 106

33. Составь цепочку из пяти чисел: первое число 15, а каждое следующее на 20 больше предыдущего.
Ответ:
15 + 20 = 35 35 + 20 = 55 55 + 20 = 75 75 + 20 = 95
Цепочка: 15, 35, 55, 75, 95

34. Не отрывая карандаша от бумаги и не проводя два раза одну и ту же линию, обведи каждую фигуру.
Ответ:

35. Начерти какой-нибудь четырёхугольник. Проведи отрезок так, чтобы он разделил данный четырёхугольник:
1) на два треугольника;
2) на треугольник и четырёхугольник.
Ответ:
​​​​​​​

36. Измерь длины сторон многоугольников и найди периметры этих фигур двумя способами.
Ответ:

37. Начерти от руки треугольник, квадрат, круг, пятиугольник.
Ответ:
​​​​​​​Самостоятельное выполнение

📹 Видео

Как правильно решить задание про четырёхугольник? / Разбор заданий на ОГЭ по геометрииСкачать

Решение планиметрических задач повышенного уровня сложностиСкачать

ВСЯ ГЕОМЕТРИЯ 8 КЛАСС ЗА 15 МИНУТ / АТАНАСЯН / К ОГЭСкачать

ЕГЭ. Математика. Четырехугольники. ПрактикаСкачать

Геометрия 8 класс // Основное содержание // Весь 8 класс с нуля за 2 урока // Доступно и наглядноСкачать

Прорешиваем книгу Акопяна - "Геометрия в картинках". Часть 1 | Василий МокинСкачать

Задача № 25 из ОГЭ по математике на доказательствоСкачать

Чему равна сумма углов выпуклого многоугольникаСкачать