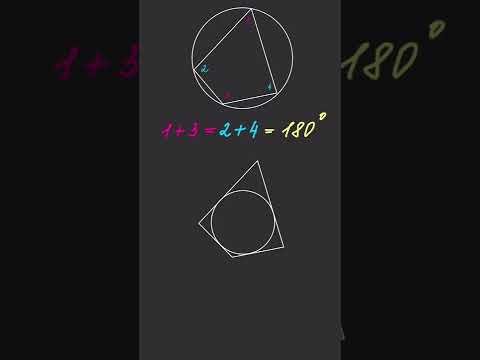Реферат по геометрии на тему четырехугольник

Автор работы: Пользователь скрыл имя, 18 Апреля 2011 в 22:27, реферат

Описание

Четырехугольник — геометрическая фигура с четырьмя сторонами. Четырехугольником называется фигура, которая состоит из четырех точек и четырех последовательно соединяющих их отрезков. При этом никакие три из данных точек не лежат на одной прямой, а соединяющие их отрезки не должны пересекаться.

Работа состоит из 1 файл

Видео:Как решить любую задачу с четырёхугольниками? | Математика TutorOnlineСкачать

Четырехугольник.docx

Четырехугольник — геометрическая фигура с четырьмя сторонами. Четырехугольником называется фигура, которая состоит из четырех точек и четырех последовательно соединяющих их отрезков. При этом никакие три из данных точек не лежат на одной прямой, а соединяющие их отрезки не должны пересекаться. Данные точки называются вершинами четырехугольника, а соединяющие их отрезки — сторонами четырехугольника.

На рисунке изображен четырехугольник. Четырехугольник обозначается указанием его вершин, причем рядом стоящие в обозначении вершины должны лежать на одной стороне. Сторонами четырехугольника являются отрезки АВ, ВС, СЕ и ЕА, вершинами — точки А, В, С и Е, углами — ©А, ©В, ©С и ©Е. Стороны АВ и ВС являются соседними сторонами, а углы ©В и ©С — соседними углами. Стороны АВ и СЕ — противоположные.
Если четырехугольник лежит по одну сторону относительно прямой, содержащей любую из его сторон, то он называется выпуклым.
Отрезок АС называется диагональю данного четырехугольника, так как содержит две противолежащие вершины.
В предыдущей главе предметом нашего рассмотрения были треугольники и их свойства. В настоящей главе мы изучим свойства четырехугольников. Заметим, что если мы разобьем четырехугольник на треугольники с помощью диагоналей, то сможем применить известные нам свойства треугольников для описания свойств четырехугольников. Следующие определения описывают несколько специальных видов четырехугольников.

Параллелограммом называется четырехугольник, противоположные стороны которого попарно параллельны, то есть лежат на параллельных прямых.

Ромб — параллелограмм, у которого все стороны равны.

Прямоугольник — параллелограмм, у которого все углы прямые.

Квадрат — прямоугольник, у которого все стороны равны.

Трапецией называется четырехугольник, у которого только две противолежащие стороны параллельны. Параллельные стороны называются основаниями трапеции. Две другие стороны называются боковыми сторонами. Трапеция, у которой боковые стороны равны, называется равнобокой.

Параллелограмм — четырехугольник, у которого противолежащие стороны попарно параллельны.

Диагональ параллелограмма делит его на два равных треугольника.

Противоположные стороны параллелограмма равны.

Противолежащие углы параллелограмма равны.

Соседние углы параллелограмма дополняют друг друга до 180».

Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам.

Если в четырехугольнике противолежащие стороны равны, то четырехугольник — параллелограмм.

Если в четырехугольнике противолежащие углы равны, то четырехугольник — параллелограмм.

Если диагонали четырехугольника пересекаются и точкой пересечения делятся пополам, то этот четырехугольник — параллелограмм.

Если в четырехугольнике две противоположные стороны параллельны и равны, то этот четырехугольник — параллелограмм.

Ромб — параллелограмм, у которого все стороны равны.

Так как ромб является параллелограммом, то для него справедливы все свойства параллелограмма. Таким образом, все теоремы, сформулированные в предыдущем разделе для параллелограммов, верны также и для ромбов. Кроме того, по определению все стороны ромба равны. Далее мы приведем две теоремы, которые характеризуют дополнительные свойства ромбов.

Параллелограмм является ромбом тогда и только тогда, когда его диагонали пересекаются под прямым углом.

Параллелограмм является ромбом тогда и только тогда, когда его диагонали являются биссектрисами его углов.

Прямоугольники и квадраты.

Прямоугольник — параллелограмм, у которого все углы прямые.

Квадрат — прямоугольник, у которого все стороны равны.

Параллелограмм является прямоугольником тогда и только тогда, когда его диагонали равны.

Средняя линия треугольника, соединяющая середины двух данных сторон, параллельна третьей стороне и равна ее половине.

1. Пусть ABCE параллелограмм, тогда:
a) Диагональ делит ABCE на два равных треугольника
b) Противолежащие стороны равны
c) Противолежащие углы равны
d) Диагонали пересекаются и точкой пересечения делятся пополам

2. Пусть ABCE прямоугольник, тогда:
a) Диагональ делит ABCE на два равных треугольника
b) Противолежащие стороны равны
c) Противолежащие углы равны
d) Диагонали пересекаются и точкой пересечения делятся пополам
e) Диагонали равны

3. Пусть ABCE ромб, тогда:
a) Диагональ делит ABCE на два равных треугольника
b) Противолежащие стороны равны
c) Противолежащие углы равны
d) Диагонали пересекаются и точкой пересечения делятся пополам
e) Диагонали перпендикулярны
f) Все стороны равны
g) Диагонали ромба делят его углы пополам

4. Пусть ABCE квадрат, тогда:
a) Диагональ делит ABCE на два равных треугольника
b) Противолежащие стороны равны
c) Противолежащие углы равны
d) Диагонали пересекаются и точкой пересечения делятся пополам
e) Диагонали равны
f) Диагонали перпендикулярны
g) Диагонали квадрата делят его углы пополам
h) Все стороны равны

Трапеция, у которой боковые стороны равны, называется равнобокой.

Трапецией называется четырехугольник, у которого только две противолежащие стороны параллельны. Параллельные стороны называются основаниями трапеции. Две другие стороны называются боковыми сторонами. Трапеция, у которой боковые стороны равны, называется равнобокой.

На данном рисунке изображена равнобокая трапеция ABCE. Параллельные стороны, BC и AE, являются основаниями. AB и CE — равные боковые стороны.

Следующие теоремы описывают свойства равнобоких трапеций.

В равнобокой трапеции углы при основании равны.

Диагонали равнобокой трапеции равны.

Средняя линяя трапеции: отрезок, соединяющий середины боковых сторон трапеции, называется средней линией трапеции.

Средняя линия трапеции параллельна основаниям и равна их полусумме.

Многоугольник — геометрическая фигура с несколькими сторонами.

Многоугольник — геометрическая фигура, состоящая из трех или более отрезков, лежащих в одной плоскости; каждый отрезок пересекает ровно два других отрезка в их концах, которые являются концами данного отрезка; никакие два пересекающихся отрезка не лежат на одной прямой. Многоугольник называется выпуклым, если он лежит в одной полуплоскости относительно любой прямой, содержащей его сторону.

3 стороны треугольник 8 сторон восьмиугольник
4 стороны четырехугольник 9 сторон девятиугольник
5 сторон пятиугольник 10 сторон десятиугольник
6 сторон шестиугольник 20 сторон двадцатиугольник
7 сторон семиугольник n сторон n-угольник

Выпуклый многоугольник называется правильным, если у него все стороны равны и все углы равны.

Сумма углов выпуклого n-угольника равна (n — 2)ј180».

Внешним углом выпуклого многоугольника при данной вершине называется угол, смежный внутреннему углу многоугольника при этой вершине. У n- угольника 2n внешних
углов.

Сумма всех внешних углов выпуклого многоугольника равна 720».

Градусная мера любого внешнего угла правильного n-угольника равна 360»/n.

Градусная мера любого внутреннего угла правильного n-угольника равна (n — 2)180»/n.

Периметром многоугольника называется сумма длин его сторон. Для того, чтобы найти периметр прямоугольника необходимо сложить длины всех его сторон.

Видео:8 класс, 3 урок, ЧетырехугольникСкачать

Свойства

• Сумма углов четырёхугольника равна 2 π = 360°.
• Четырёхугольник можно вписать в окружность тогда и только тогда, когда сумма противоположных углов равна 180° ( ). См. также теорема Птолемея .
• Четырёхугольник является описанным около окружности тогда и только тогда, когда суммы длин противоположных сторон равны ( )
• Формула Эйлера: учетверённый квадрат расстояния между серединами диагоналей равен сумме квадратов сторон четырёхугольника минус сумму квадратов его диагоналей.
• Средние линии четырёхугольника и отрезок, соединяющий середины его диагоналей, пересекаются в одной точке и делятся ею пополам.
• Четыре отрезка, каждый из которых соединяет вершину четырёхугольника с центроидом треугольника, образованного оставшимися тремя вершинами, пересекаются в центроиде четырёхугольника и делятся им в отношении 3:1, считая от вершин.
• Две противоположные стороны четырёхугольника перпендикулярны тогда и только тогда, когда сумма квадратов двух других противоположных сторон равна сумме квадратов диагоналей.
• Диагонали четырёхугольника перпендикулярны тогда и только тогда, когда суммы квадратов противоположных сторон равны.
• Средние линии четырёхугольника равны тогда и только тогда, когда равны суммы квадратов его противоположных сторон.
• См. также свойства центроида четырёхугольника.
• Шесть расстояний между четырьмя произвольными точками плоскости, взятыми попарно, связаны соотношением:

Его можно представить ещё в виде:

Видео:Четырехугольник | Геометрия 7-9 класс #41 | ИнфоурокСкачать



[ править ] Площадь

Площадь произвольного четырёхугольника с диагоналями d₁, d₂ и углом α между ними (или их продолжениями), равна:

Площадь произвольного выпуклого четырёхугольника равна:

• , где e, f — длины диагоналей, a, b, c, d — длины сторон.
• , где p — полупериметр. Из этой формулы для вписанных 4-угольников следует формула Брахмагупты .

[ править ] Особые случаи

Если 4-угольник и вписан и описан, то .

[ править ] История

В древности египтяне и некоторые другие народы использовали в качестве площади четырёхугольника неверную формулу — произведение полусумм его противоположных сторон a, b, c, d [1] :

Видео:Вписанные и описанные четырехугольники. Практическая часть. 9 класс.Скачать



Курсовая работа по теме «Четырехугольники»

Видео:Миникурс по геометрии. ЧетырехугольникиСкачать



«Управление общеобразовательной организацией:
новые тенденции и современные технологии»

Свидетельство и скидка на обучение каждому участнику

Министерство образования и науки

донецкой народной республики

Государственное образовательное учреждение

высшего профессионального образования

«донецкий национальный университет»

Факультет математики и информационных технологий

учебная курсовая работа

по методике обучения математике

на тему: «Проектирование изучения темы «Четырехугольники» в 8 классе общеобразовательной школы»

Студентка группы 44.03.05 Педагогическое образование на основе ВПО

Долгова Елена Владимировна ___________________________

Проверила: к. пед. н., доц.

Видео:ГЕОМЕТРИЯ 8 класс: Четырехугольники | Видеоурок с теорией и решением задачиСкачать



ПОСТАНОВКА ЦЕЛЕЙ ОБУЧЕНИЯ ТЕМЕ

«Четырехугольники» (10 часов)

Цель изучения темы: дать систематизированные сведения о четырехугольниках и их свойствах; их элементах; о параллелограмме и его свойствах; признаках параллелограмма; о прямоугольнике, ромбе, квадрате и их свойствах; о трапеции и ее свойствах; осевой и центральной симметрии.

В результате изучения темы ученики должны уметь (табл. 1.):

Различать из данных фигур выпуклый многоугольник.

Определить какой из данных многоугольников является выпуклым на рис.2.

Определять из данных фигур четырехугольник.

Определить из данных фигур четырехугольник на рис. 3.

Определять из данных фигур параллелограмм.

Определить из данных фигур на рис. 4 параллелограмм.

Определять из данных фигур трапецию.

Определить их данных фигур на рис. 5 трапецию.

Определять из данных фигур равнобедренную трапецию.

Определить из данных фигур на рис. 6 равнобедренную трапецию.

Различать из данных фигур прямоугольную трапецию.

Определить из данных фигур на рис. 7 прямоугольную трапецию.

Различать из данных фигур прямоугольник.

Определить из данных фигур на рис. 8 прямоугольник.

Определять из данных фигур ромб.

Определить из данных фигур на рис. 9 ромб.

Определять из данных фигур квадрат.

Определить из данных фигур на рис. 10 квадрат.

Определять фигуры симметричные относительно прямой.

Какие из данных фигур на рис. 11 имеют осевую симметрию относительно прямой.

Строить точки симметричные относительно точек.

Какие из данных фигур на рис. 12 имеют осевую симметрию относительно точек.

Находить сумму углов многоугольника по формуле

Найти сумму углов шестиугольника.

Находить внешние углы выпуклого многоугольника если их сумма 360 о

Найти внешние углы правильного шестиугольника на рис.13.



Находить сумму углов выпуклого четырехугольника

Сумма трех углов четырехугольника равна 270 о . Найти четвертый угол.

Находить равные элементы параллелограмма.

Найти углы в параллелограмме АВСD, если А=84 о

Решать задачи использую свойство диагоналей параллелограмма.

Диагонали параллелограмма АС=4см, BD=6см и пересекаются в точке О под углом 60 о . Найти площадь треугольника АОD.

Решать задачи используя свойство параллелограмма о равных и параллельных сторонах.

В четырехугольнике ABCD AB=CD и AB CD. Докажите, что четырехугольник ABCD – параллелограмм.

Решать задачи используя свойство равенства противоположных сторон параллелограмма.

В четырехугольнике ВСОЕ стороны ВС и ОЕ параллельны, а углы В и С равны 90 ْ . Является ли четырехугольник ВСОЕ параллелограммом?

Решать задачи используя свойство диагоналей, которые пересекаются и точкой пересечения делятся пополам.

Точка пересечения диагоналей четырехугольника ВСКМ не является серединой одной из них. Может ли этот четырехугольник быть параллелограммом?

Решать задачи используя свойство равенства противолежащих сторон.

У параллелограмма ABCD АВ = 10см, ВС=15см. Чему равны стороны АD и СD?

Решать задачи используя свойство равенства противолежащих углов.

У параллелограмма ABCD А=30 о . Чему равны углы В, С и D?

Решать задачи используя свойство средней линии трапеции.

Основания трапеции относятся как 2:3, а средняя линия равна 5м. Найти основания.

Решать задачи используя свойство диагоналей прямоугольника.

Найти диагонали прямоугольника, если их сумма равна 12см.

Решать задачи используя свойство ромба о диагоналях, которые взаимно перпендикулярны и делят углы пополам.

ABCD – ромб (рис. 14) по данным на рисунке найти углы АВС, ВСD и АОВ

Решать задачи используя свойство диагоналей ромба пересекаться под прямым углом.

ABCD – ромб (рис. 15) по данным на рисунке найти углы ВОА, ВОС, COD и DOA.

Решать задачи используя свойство диагоналей ромба являются биссектрисами его углов.

ABCD – ромб (рис. 16) угол ОВС = 60 о Найти все углы ромба.

Решать задачи по свойству прямых углов квадрата.

ABCD – квадрат (рис. 17). Угол А= 90 о . Найти углы B, C, D.

Решать задачи по свойству диагоналей квадрата.

ABCD – квадрат (рис. 18), АО = 3см, угол АВО = 45 о . Найти АС, ВD, углы СОD, АDС

Видео:ЧЕТЫРЕХУГОЛЬНИК и его элементы. §1 геометрия 8 классСкачать



2. ПРОЕКТИРОВАНИЕ ИЗУЧЕНИЯ ТЕОРЕТИЧЕСКОГО МАТЕРИАЛА

Видео:ОПИСАННЫЙ ЧЕТЫРЕХУГОЛЬНИК. Подготовка к ЕГЭ ЧАСТЬ I #shorts #егэ #огэ #математика #геометрияСкачать



2.1. Тематическое планирование

В табл. 2 предложено календарное планирование уроков [9].

Многоугольники, выпуклый многоугольник

Параллелограмм, признаки параллелограмма

Осевая и центральная симметрии

Тематическая контрольная работа

Анализ тематической контрольной работы. Подведение итогов изучения темы

Учебник: Геометрия. 7-9 классы: учеб. для общеобразоват. организациий/[Л.С. Анатасян, В.Ф. Бутузов, С.Б. Кадомцев и др.]. – 6-е изд. – М.: Просвещение, 2016. – 383с.

Видео:Четырехугольники. Геометрия 8 класс.Скачать



2.2. Математические определения

В табл. 3 предложены понятия по данной теме [2;7].

Если несмежные звенья замкнутой ломаной не имеют общих точек, то эта ломанная называется многоугольником .

Многоугольник называется выпуклым , если он лежит по одну сторону от каждой прямой, проходящей через две его соседние вершины.

Четырехугольником называется фигура, которая состоит из четырех точек и четырех последовательно соединяющих их отрезков.

Параллелограммом называется четырехугольник, у которого противоположные стороны попарно параллельны .

Трапецией называется четырехугольник, у которого две стороны параллельны, а две другие стороны не параллельны.

Трапеция называется равнобедренной , если ее боковые стороны равны.

Трапеция , один из углов которой прямой, называется прямоугольной .

Прямоугольником называется параллелограмм, у которого все углы прямые.

Ромбом называется параллелограмм, у которого все стороны равны.

Квадратом называется прямоугольник, у которого все стороны равны.

Фигура называется симметричной относительно прямой a, если для каждой точки фигуры симметричная ей точка относительно прямой a также принадлежит этой фигуре.

Фигура называется симметричной относительно точки О, если для каждой точки фигуры симметричная ей точка относительно точки О также принадлежит этой фигуре.

Видео:Четырехугольники, вписанные в окружность. 9 класс.Скачать



2.3. Математические теоремы

В табл. 4 предложены теоремы по данной теме [2;7].

Сумма углов выпуклого n-угольника равна

Сумма внешних углов выпуклого многоугольника равна 360 о

Сумма углов выпуклого четырехугольника равна 360 о

В параллелограмме противоположные стороны равны и противоположные углы равны.

Диагонали параллелограмма точкой пересечения делятся пополам.

Если в четырехугольнике две стороны равны и параллельны, то этот четырехугольник – параллелограмм.

Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник – параллелограмм.

Если в четырехугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырехугольник – параллелограмм.

У параллелограмма противолежащие стороны равны, противолежащие углы равны.

Средняя линия трапеции параллельна основаниям и равна их полусумме.

Диагонали прямоугольника равны

Диагонали ромба взаимно перпендикулярны и делят его углы пополам.

Диагонали ромба пересекаются под прямым углом.

Диагонали ромба являются биссектрисами углов.

Все углы квадрата прямые.

Диагонали квадрата равны, взаимно перпендикулярны, точкой пересечения делятся пополам и делят углы квадрата пополам.

Теорема из учебника в категорической форме : В параллелограмме противоположные стороны равны и противоположные углы равны.

Теорема в импликативной форме : если четырехугольник является параллелограммом, то в нем противоположные стороны равны и противоположные углы равны.

а) разъяснительная часть: четырехугольник

б) условие: параллелограмм

в) заключение: противоположные стороны равны и противоположные углы равны.

Характеристика теоремы : сложная, т.к. имеет одно условие и два заключения.

Если в четырехугольнике противоположные стороны равны и противоположные углы равны, то он является параллелограммом (истинность).

Если в четырехугольнике противоположные стороны не равны или противоположные углы не равны, то он не является параллелограммом (истинность).

Противоположное обратному утверждение:

Если четырехугольник не параллелограмм, то его противоположные стороны не равны или противоположные углы не равны (истинность).

Видео:Четырёхугольник и его элементы – 8 класс геометрияСкачать



3. МЕТОДИКА ФОРМИРОВАНИЯ ПОНЯТИЯ

Понятие «трапеция» вводится на уроке № 4

Способ введения понятия: конкретно-индуктивный.

Видео:Геометрия 8 класс (Урок№1 - Многоугольники. Четырёхугольник.)Скачать



І. Этап введения

Видео:ЧЕТЫРЕХУГОЛЬНИК 8 класс РЕШЕНИЕ ЗАДАЧ АтанасянСкачать



3.1. Мотивация необходимости введения понятия

Слово «трапеция» присутствует не только в геометрии, она имеет более широкое применение в повседневной жизни.

Это необычное слово мы можем встретить, просматривая спортивные соревнования гимнастов, выполняющих акробатические упражнения на трапеции. В гимнастике трапецией называют спортивный снаряд, который состоит из перекладины, подвешенной на двух веревках.

Также это слово можно услышать, занимаясь в спортивном зале или в среде людей, которые занимаются бодибилдингом, так как трапеции — это не только геометрическая фигура или спортивный акробатический снаряд, но и мощные мышцы спины, которые расположены сзади за шеей.



На рис. 19 изображена воздушная трапеция, которую изобрел для цирковых акробатов артист Джулиус Леотард еще в девятнадцатом веке во Франции. Вначале создатель этого номера устанавливал свой снаряд на небольшой высоте, но в итоге он был перенесен под самый купол цирка.

Воздушные гимнасты в цирке выполняют трюки перелетов из трапеции на трапецию, исполняют перекрёстные полёты, проделывают в воздухе сальто-мортале.

В конном виде спорта, трапецией называют упражнение для растяжки или потягивание тела лошади, которое очень полезно и приятно для животного. Во время стойки лошади в положении трапеции работает растяжка ног животного или мышц его спины. Это красивое упражнение мы можем наблюдать во время поклона или так называемого «переднего кранча», когда лошадь глубоко прогибается.

Впервые в 1947 году известный французский модельер Кристиан Диор произвел показ мод, в котором присутствовал силуэт юбки-трапеции. И хотя уже прошло более шестидесяти лет, этот силуэт до сих пор в моде, и не теряет своей актуальности, и по сей день.

В гардеробе английской королевы юбка-трапеция стала непременным предметом и ее визитной карточкой.

Напоминающая геометрическую форму трапеции, юбка с одноименным названием прекрасно сочетается с любыми кофточками, блузами, топами и пиджаками. Классичность и демократичность этого популярного фасона позволяет ее носить и со строгими пиджаками и немного легкомысленными топами. В такой юбке будет уместно появляться как в офисе, так и на дискотеке.

Название такой необычной фигуры, как «трапеция» произошло от слова «трапезион», что в переводе с греческого языка, обозначает слово «столик», от которого произошли также слово «трапеза» и другие родственные слова.

Ознакомление с существенными свойствами трапеции может осуществляться посредством предъявления учителем рисунка, на котором изображены различные четырехугольники, и выделения учащимися тех из них, у которых две стороны параллельны, а две другие нет (рис.20).





Рассматривая эти рисунки, учащиеся должны ответить на вопрос: «Какие из данных фигур имеют общие свойства?» Ребята замечают, что в четырехугольниках а, б, г, д, и две противоположные стороны параллельны, а две другие нет [6].

Введение понятия трапеция может быть введено и путем выполнения упражнений на построение различных четырехугольников, в том числе и четырехугольников у которых две стороны параллельны, а две другие нет.

Видео:3 правила для вписанного четырехугольника #shortsСкачать



3.2. Актуализация знаний и умений учащихся,
необходимых для сознательного усвоения понятия

То, что необходимо повторить

Задания для повторения

Дать понятие параллельных прямых.

Начертить две параллельные прямые a и b.

Дать понятие параллелограмма и его элементов.

Нарисовать параллелограмм ABCD. Назвать прилежащие углы к стороне АВ.

Прилежащие и противолежащие элементы параллелограмма.

Назовите угол который лежит между сторонами АВ и ВС.

Признаки параллельности двух прямых

Решение задач на готовых чертежах [8]:

1. На рис. 21. Найти х

2. На рис. 22. Найти у

3. На рис. 23. Найти z







Видео:Геометрия 10 класс (Урок№2 - Четырехугольники.)Скачать



3.3. Подведение учащихся к формулировке определения понятия

Вот теперь мы подошли к действию подведения под понятие.

Учитель на доске изображает 5 фигур (рис. 24) и предлагает классу посмотреть на доску.

Как вы считаете, какая из фигур являются трапецией? Зарисуйте трапецию в тетради.

Учитель на доске изображает еще 5 фигур (рис. 25) и предлагает найти из данных фигур равнобокую трапецию. Ученики опять зарисовывают в тетради.

Учитель на доске изображает еще 5 фигур (рис. 26) и предлагает найти из данных фигур прямоугольную трапецию. Ученики зарисовывают в тетради.

Учителем выдвигается гипотеза: трапеция – четырехугольник, у которого противолежащие стороны параллельны. Найдите ошибку в определении.

Ученики дают правильное определение: Трапеция – четырехугольник, у которого две стороны параллельны, а две другие стороны не параллельны.

Учитель: сформулируйте определения равнобедренной и прямоугольной трапеции.

Ученики: Трапеция называется равнобедренной, если ее боковые стороны равны.

Трапеция , один из углов которой прямой, называется прямоугольной.

Учитель предлагает ученикам привести примеры трапеции в повседневной жизни.

Ученики приводят примеры: в интерьерах (диваны, стены, навесные потолки); в ландшафтном дизайне (границы газонов, искусственных водоемов, камней); в индустрии моды (одежда, обувь, аксессуары); в дизайне предметов повседневного пользования (светильники, посуда, с использованием форм трапеции); в архитектуре.

Видео:8 класс, 9 урок, Осевая и центральная симметрияСкачать



ІІ. Этап усвоения

Видео:Параллелограмм, прямоугольник, ромб,квадрат,трапеция, все свойства и определения!!!Скачать



3.4. Формулировка определения, овладение его содержанием

Трапецией называется четырехугольник, у которого две стороны параллельны, а две другие стороны не параллельны.

Если у четырехугольника две стороны параллельны, а другие две не параллельны, то такой четырехугольник называется трапецией.

Четырехугольник в котором две противолежащие стороны параллельны, а две другие не параллельны называется трапецией.

Низкий столик для еды сбоку имел вид фигуры с двумя параллельными сторонами. Греки сначала называли его «тетрапецион» – четырехногий, а потом название сократилось до «трапезион» (и сейчас иногда говорят «трапеза» вместо еды). Поэтому фигуру такого вида назвали трапецией.

В «Началах» (главный труд Евклида, написанный около 300 г. до н.э. и посвященный систематическому построению трапеции) термин «трапеция» применяется не в современном смысле, а в другом смысле: любой четырехугольник (не параллелограмм).

В современном смысле термин встречается впервые у древнегреческого математика Посидония. У Прокла этим словом названа только трапеция, а все прочие четырехугольники называются «трапециевидные» — τραπεζοεδης [1].

Трапецией называется четырехугольник, у которого две стороны параллельны, А две другие стороны не параллельны.

На рис. 27 представлены несколько видов трапеции.

Видео:Геометрия 8. Урок 12 - Площадь четырехугольников. Формулы.Скачать



геометрия четырехугольника

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ОБРАЗОВАНИЯ
«НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ПЕДАГОГИЧЕСКИЙ УНИВЕРСИТЕТ»
ИНСТИТУТА ФИЗИКО-МАТЕМАТИЧЕСКОГО И ИНФОРМАЦИОННО-ЭКОНОМИЧЕСКОГО ОБРАЗОВАНИЯ
КАФЕДРА ГЕОМЕТРИИ И МЕТОДИКИ ОБУЧЕНИЯ МАТЕМАТИКЕ

ГЕОМЕТРИЯ ЧЕТЫРЕХУГОЛЬНИКА
Курсовая работа по дисциплине:элементарная геометрия

Выполнил студент группы 41
А.Д. Куликова ___________
(подпись, дата)
Направление подготовки 44.03.01 Педагогическое образование
Профиль Математическое образование
Форма обучения Очная

Научный руководитель
ст. преподаватель кафедры
геометрии и МОМ
М.Н.Сухоносенко
______________
(подпись)
_____________
(оценка)
___ ________ 20__г.

СодержаниеВведение…………………………………………………………………….3
1. Теоретический аспект понятия «четырехугольники» в школьном курсе геометрии…………………………………………………………………. 4
1.1. Произвольный четырехугольник…………………………………..4
1.2. Виды четырехугольников, их свойства и признаки………………5
2. Совершенный квадрат……………………………………………. 20
2.1. Понятие совершенный квадрат……………………………………20
2.2. Методы построения………………………………………………..21
3. Решениезадач………………………………………………………24
Заключение………………………………………………………………..30
Список используемой литературы………………………………………31

Введение
В современном мире нас окружают различные геометрические фигуры: треугольник, окружность, квадраты и многие другие. Но, чаще все же встречаются предметы четырехугольной формы.
Четырехугольник является основной фигурой. Изучение его свойств обычно не вызываютзатруднений. Для развития и формирования логического мышления учащихся используется сведенья о параллелограммах и их частных видах. Поэтому актуально рассмотреть понятие четырехугольника более подробно.
Целью данной курсовой работы является систематизация знаний о четырехугольнике и применение их для решения геометрических задач.
Цель достигается путем решения следующих задач:
1. Изложить определение понятия«четырехугольник».
2. Описать классификацию четырехугольников школьного курса математики.
3. Рассмотреть и описать методы доказательства свойств и признаков некоторых видов четырехугольников.
4. На примере решения задач по математике рассмотреть работу данных методов на практике.

1. Теоретический аспект понятия «четырехугольники» в школьном курсе геометрии
1.1 Произвольный четырехугольник
На самых первыхуроках геометрии формируется представление о некоторых геометрических фигурах. Такие фигуры, как круг, треугольник, прямоугольник и др., измерение отрезков и углов — это только начальные геометрические сведения.
Определение четырехугольника вводится в зависимости от того, как и когда введено понятие многоугольника. Например, Л. С. Атанасян дает понятие четырехугольник как частный вид многоугольника. У А. В.Погорелова определение четырехугольника звучит подобно определению треугольника: «Четырехугольником называется фигура, которая состоит из четырех точек и четырех последовательно соединяющих их отрезков. При этом никакие три из данных точек не лежат на одной прямой, а соединяющие их отрезки не должны пересекаться», поскольку понятие многоугольника вводится значительно позже.
Если обратиться кистории, то мы увидим, что такие виды четырехугольников, как прямоугольник, квадрат, трапеция встречались уже в документах Древнего Египта и Вавилона.
Четырехугольником называется фигура, которая состоит из четырех точек и четырех последовательно соединяющих их отрезков. При этом никакие три из данных точек не лежат на одной прямой, а соединяющие их отрезки не пересекаются.
Две несмежные сторонычетырехугольника называются противоположными. Две вершины, не являющиеся соседними, называются также противоположными.
Четырехугольники делятся на выпуклые и невыпуклые.
Четырёхугольник называется выпуклым (Рис.1), если он лежит по одну сторону от любой прямой, проходящей через любые две его смежные вершины. В противном случае четырёхугольник называется.

Чтобы читать весь документ, зарегистрируйся.

🎥 Видео

свойства вписанного и описанного четырехугольника #SHORTSСкачать