 Вписанные и центральные углы Вписанные и центральные углы |
 Углы, образованные хордами, касательными и секущими Углы, образованные хордами, касательными и секущими |
 Доказательства теорем об углах, связанных с окружностью Доказательства теорем об углах, связанных с окружностью |
- Вписанные и центральные углы
- Теоремы о вписанных и центральных углах
- Теоремы об углах, образованных хордами, касательными и секущими
- Доказательства теорем об углах, связанных с окружностью
- Окружность. Основные теоремы
- Угол между прямыми онлайн
- Предупреждение
- 1. Угол между прямыми на плоскости
- Прямые заданы каноническими уравнениями
- 1.1. Определение угла между прямыми
- 1.2. Условие параллельности прямых
- 1.3. Условие перпендикулярности прямых
- Прямые заданы общими уравнениями
- 1.4. Определение угла между прямыми
- 1.5. Условие параллельности прямых
- 1.6. Условие перпендикулярности прямых
- 2. Угол между прямыми в пространстве
- 2.1. Определение угла между прямыми
- 2.2. Условие параллельности прямых
- 2.3. Условие перпендикулярности прямых
- 📸 Видео
Видео:Угол между прямыми в пространстве. 10 класс.Скачать

Вписанные и центральные углы
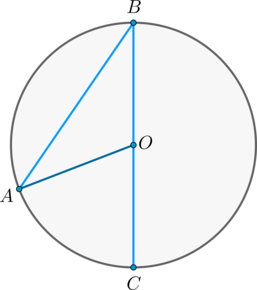
Определение 1 . Центральным углом называют угол, вершина которого совпадает с центром окружности, а стороны являются радиусами радиусами (рис. 1).
Определение 2 . Вписанным углом называют угол, вершина которого лежит на окружности, а стороны являются хордами хордами (рис. 2).
Напомним, что углы можно измерять в градусах и в радианах. Дуги окружности также можно измерять в градусах и в радианах, что вытекает из следующего определения.
Определение 3 . Угловой мерой (угловой величиной) дуги окружности является величина центрального угла, опирающегося на эту дугу.
Видео:Угол между прямой и плоскостью. Видеоурок по геометрии 10 классСкачать

Теоремы о вписанных и центральных углах
| Фигура | Рисунок | Теорема | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Вписанный угол |  | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Вписанный угол |  | Вписанные углы, опирающиеся на одну и ту же дугу равны. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Вписанный угол |  | Вписанные углы, опирающиеся на одну и ту же хорду, равны, если их вершины лежат по одну сторону от этой хорды | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Вписанный угол |  | Два вписанных угла, опирающихся на одну и ту же хорду, в сумме составляют 180° , если их вершины лежат по разные стороны от этой хорды | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Вписанный угол |  | Вписанный угол является прямым углом, тогда и только тогда, когда он опирается на диаметр | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Окружность, описанная около прямоугольного треугольника |  |
| Вписанный угол | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Окружность, описанная около прямоугольного треугольника | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Фигура | Рисунок | Теорема | Формула |
| Угол, образованный пересекающимися хордами |  |  | |
| Угол, образованный секущими, которые пересекаются вне круга |  |  | |
| Угол, образованный касательной и хордой, проходящей через точку касания |  |  | |
| Угол, образованный касательной и секущей |  |  | |
| Угол, образованный двумя касательными к окружности |  |  |
| Угол, образованный пересекающимися хордами хордами | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Формула:  | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Угол, образованный секущими секущими , которые пересекаются вне круга | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Формула:  | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Величина угла, образованного секущими, пересекающимися вне круга, равна половине разности величин дуг, заключённых между его сторонами | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Угол, образованный касательной и хордой хордой , проходящей через точку касания | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Формула:  | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Угол, образованный касательной и секущей касательной и секущей | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Формула:  | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Величина угла, образованного касательной и секущей, равна половине разности величин дуг, заключённых между его сторонами | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Угол, образованный двумя касательными касательными к окружности | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Формулы:  | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
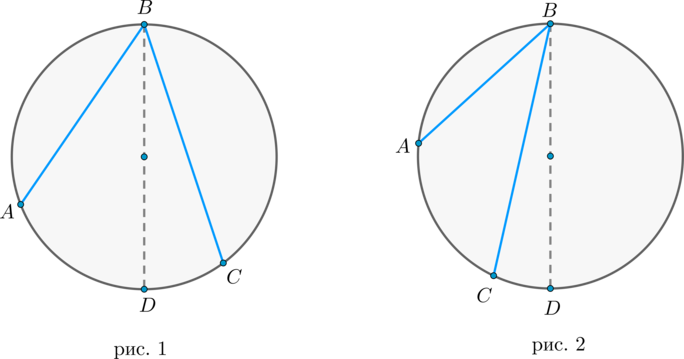
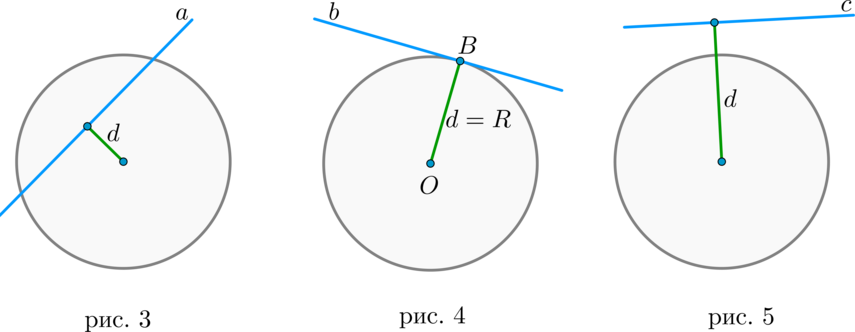
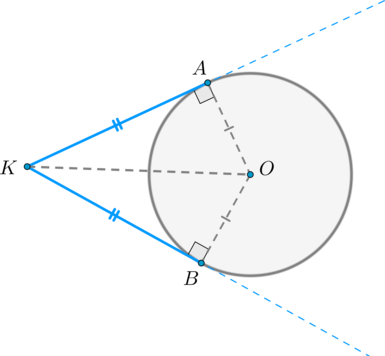
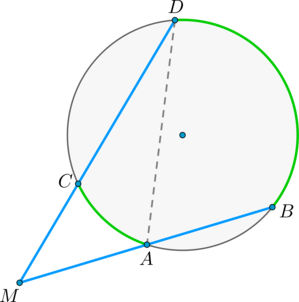
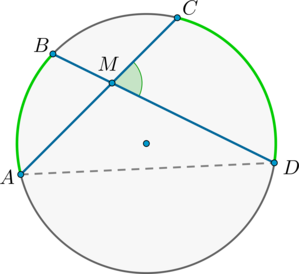
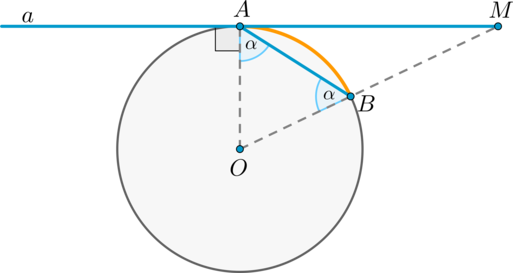
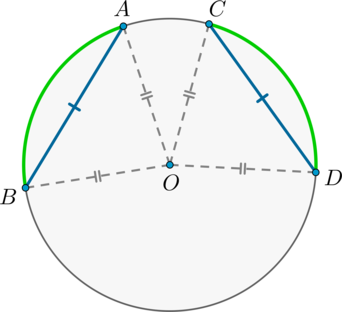
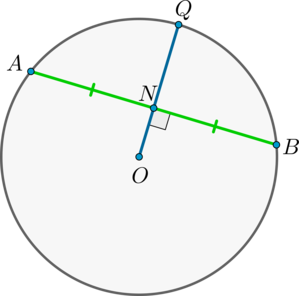
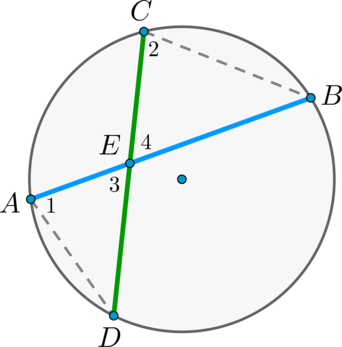
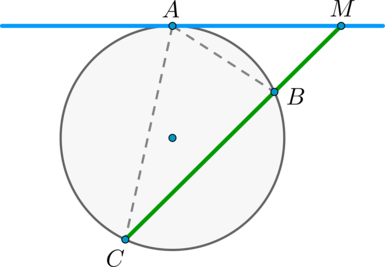
Величина угла, образованного двумя касательными к окружности, равна половине разности величин дуг, заключённых между его сторонами Видео:21. Угол между прямой и плоскостьюСкачать 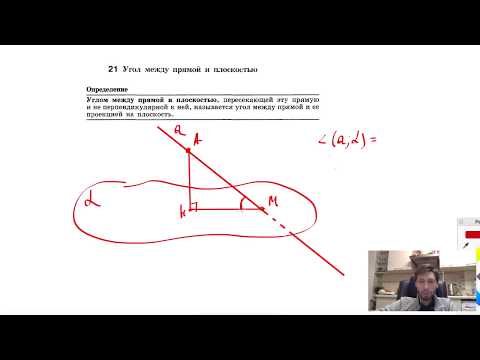 Доказательства теорем об углах, связанных с окружностьюТеорема 1 . Величина вписанного угла равна половине величины центрального угла, опирающегося на ту же дугу. Доказательство . Рассмотрим сначала вписанный угол ABC , сторона BC которого является диаметром окружности диаметром окружности , и центральный угол AOC (рис. 5). Таким образом, в случае, когда одна из сторон вписанного угла проходит через центр окружности, теорема 1 доказана. Теперь рассмотрим случай, когда центр окружности лежит внутри вписанного угла (рис. 6). В этом случае справедливы равенства и теорема 1 в этом случае доказана. Осталось рассмотреть случай, когда центр окружности лежит вне вписанного угла (рис. 7). В этом случае справедливы равенства что и завершает доказательство теоремы 1. Теорема 2 . Величина угла, образованного пересекающимися хордами хордами , равна половине суммы величин дуг, заключённых между его сторонами. Доказательство . Рассмотрим рисунок 8. Нас интересует величина угла AED , образованного пересекающимися в точке E хордами AB и CD . Поскольку угол AED – внешний угол треугольника BED , а углы CDB и ABD являются вписанными углами, то справедливы равенства что и требовалось доказать. Теорема 3 . Величина угла, образованного секущими секущими , пересекающимися вне круга, равна половине разности величин дуг, заключённых между сторонами этого угла. Доказательство . Рассмотрим рисунок 9. Нас интересует величина угла BED , образованного пересекающимися в точке E секущими AB и CD . Поскольку угол ADC – внешний угол треугольника ADE , а углы ADC , DCB и DAB являются вписанными углами, то справедливы равенства что и требовалось доказать. Теорема 4 . Величина угла, образованного касательной и хордой касательной и хордой , проходящей через точку касания, равна половине величины дуги, заключённой между его сторонами. Доказательство . Рассмотрим рисунок 10. Нас интересует величина угла BAC , образованного касательной AB и хордой AC . Поскольку AD – диаметр диаметр , проходящий через точку касания, а угол ACD – вписанный угол, опирающийся на диаметр, то углы DAB и DCA – прямые. Поэтому справедливы равенства что и требовалось доказать Теорема 5 . Величина угла, образованного касательной и секущей касательной и секущей , равна половине разности величин дуг, заключённых между сторонами этого угла. Доказательство . Рассмотрим рисунок 11. Нас интересует величина угла BED , образованного касательной AB и секущей CD . Заметим, что угол BDC – внешний угол треугольника DBE , а углы BDC и BCD являются вписанными углами. Кроме того, углы DBE и DCB , в силу теоремы 4, равны. Поэтому справедливы равенства что и требовалось доказать. Теорема 6 .Величина угла, образованного двумя касательными к окружности касательными к окружности , равна половине разности величин дуг, заключённых между его сторонами. Доказательство . Рассмотрим рисунок 12. Нас интересует величина угла BED , образованного касательными AB и CD . Заметим, что углы BOD и BED в сумме составляют π радиан. Поэтому справедливо равенство Видео:Угол между векторами. 9 класс.Скачать  Окружность. Основные теоремыОпределения Центральный угол – это угол, вершина которого лежит в центре окружности. Вписанный угол – это угол, вершина которого лежит на окружности. Градусная мера дуги окружности – это градусная мера центрального угла, который на неё опирается. Теорема Градусная мера вписанного угла равна половине градусной меры дуги, на которую он опирается. Доказательство Доказательство проведём в два этапа: сначала докажем справедливость утверждения для случая, когда одна из сторон вписанного угла содержит диаметр. Пусть точка (B) – вершина вписанного угла (ABC) и (BC) – диаметр окружности: Треугольник (AOB) – равнобедренный, (AO = OB) , (angle AOC) – внешний, тогда (angle AOC = angle OAB + angle ABO = 2angle ABC) , откуда (angle ABC = 0,5cdotangle AOC = 0,5cdotbuildrelsmileover) . Теперь рассмотрим произвольный вписанный угол (ABC) . Проведём диаметр окружности (BD) из вершины вписанного угла. Возможны два случая: 1) диаметр разрезал угол на два угла (angle ABD, angle CBD) (для каждого из которых теорема верна по доказанному выше, следовательно верна и для исходного угла, который является суммой этих двух и значит равен полусумме дуг, на которые они опираются, то есть равен половине дуги, на которую он опирается). Рис. 1. 2) диаметр не разрезал угол на два угла, тогда у нас появляется ещё два новых вписанных угла (angle ABD, angle CBD) , у которых сторона содержит диаметр, следовательно, для них теорема верна, тогда верна и для исходного угла (который равен разности этих двух углов, значит, равен полуразности дуг, на которые они опираются, то есть равен половине дуги, на которую он опирается). Рис. 2. Следствия 1. Вписанные углы, опирающиеся на одну и ту же дугу, равны. 2. Вписанный угол, опирающийся на полуокружность, прямой. 3. Вписанный угол равен половине центрального угла, опирающегося на ту же дугу. Определения Существует три типа взаимного расположения прямой и окружности: 1) прямая (a) пересекает окружность в двух точках. Такая прямая называется секущей. В этом случае расстояние (d) от центра окружности до прямой меньше радиуса (R) окружности (рис. 3). 2) прямая (b) пересекает окружность в одной точке. Такая прямая называется касательной, а их общая точка (B) – точкой касания. В этом случае (d=R) (рис. 4). 3) прямая (c) не имеет общих точек с окружностью (рис. 5). Теорема 1. Касательная к окружности перпендикулярна радиусу, проведенному в точку касания. 2. Если прямая проходит через конец радиуса окружности и перпендикулярна этому радиусу, то она является касательной к окружности. Следствие Отрезки касательных, проведенных из одной точки к окружности, равны. Доказательство Проведем к окружности из точки (K) две касательные (KA) и (KB) : Значит, (OAperp KA, OBperp KB) как радиусы. Прямоугольные треугольники (triangle KAO) и (triangle KBO) равны по катету и гипотенузе, следовательно, (KA=KB) . Следствие Центр окружности (O) лежит на биссектрисе угла (AKB) , образованного двумя касательными, проведенными из одной точки (K) . Теорема об угле между секущими Угол между двумя секущими, проведенными из одной точки, равен полуразности градусных мер большей и меньшей высекаемых ими дуг. Доказательство Пусть (M) – точка, из которой проведены две секущие как показано на рисунке: Покажем, что (angle DMB = dfrac(buildrelsmileover — buildrelsmileover)) . (angle DAB) – внешний угол треугольника (MAD) , тогда (angle DAB = angle DMB + angle MDA) , откуда (angle DMB = angle DAB — angle MDA) , но углы (angle DAB) и (angle MDA) – вписанные, тогда (angle DMB = angle DAB — angle MDA = fracbuildrelsmileover — fracbuildrelsmileover = frac(buildrelsmileover — buildrelsmileover)) , что и требовалось доказать. Теорема об угле между пересекающимися хордами Угол между двумя пересекающимися хордами равен полусумме градусных мер высекаемых ими дуг: [angle CMD=dfrac12left(buildrelsmileover+buildrelsmileoverright)] Доказательство (angle BMA = angle CMD) как вертикальные. Из треугольника (AMD) : (angle AMD = 180^circ — angle BDA — angle CAD = 180^circ — frac12buildrelsmileover — frac12buildrelsmileover) . Но (angle AMD = 180^circ — angle CMD) , откуда заключаем, что [angle CMD = frac12cdotbuildrelsmileover + frac12cdotbuildrelsmileover = frac12(buildrelsmileover + buildrelsmileover).] Теорема об угле между хордой и касательной Угол между касательной и хордой, проходящей через точку касания, равен половине градусной меры дуги, стягиваемой хордой. Доказательство Пусть прямая (a) касается окружности в точке (A) , (AB) – хорда этой окружности, (O) – её центр. Пусть прямая, содержащая (OB) , пересекает (a) в точке (M) . Докажем, что (angle BAM = frac12cdot buildrelsmileover) . Обозначим (angle OAB = alpha) . Так как (OA) и (OB) – радиусы, то (OA = OB) и (angle OBA = angle OAB = alpha) . Таким образом, (buildrelsmileover = angle AOB = 180^circ — 2alpha = 2(90^circ — alpha)) . Так как (OA) – радиус, проведённый в точку касания, то (OAperp a) , то есть (angle OAM = 90^circ) , следовательно, (angle BAM = 90^circ — angle OAB = 90^circ — alpha = frac12cdotbuildrelsmileover) . Теорема о дугах, стягиваемых равными хордами Равные хорды стягивают равные дуги, меньшие полуокружности. И наоборот: равные дуги стягиваются равными хордами. Доказательство 1) Пусть (AB=CD) . Докажем, что меньшие полуокружности дуги (buildrelsmileover=buildrelsmileover) . (triangle AOB=triangle COD) по трем сторонам, следовательно, (angle AOB=angle COD) . Но т.к. (angle AOB, angle COD) — центральные углы, опирающиеся на дуги (buildrelsmileover, buildrelsmileover) соответственно, то (buildrelsmileover=buildrelsmileover) . 2) Если (buildrelsmileover=buildrelsmileover) , то (triangle AOB=triangle COD) по двум сторонам (AO=BO=CO=DO) и углу между ними (angle AOB=angle COD) . Следовательно, и (AB=CD) . Теорема Если радиус делит хорду пополам, то он ей перпендикулярен. Верно и обратное: если радиус перпендикулярен хорде, то точкой пересечения он делит ее пополам. Доказательство 1) Пусть (AN=NB) . Докажем, что (OQperp AB) . Рассмотрим (triangle AOB) : он равнобедренный, т.к. (OA=OB) – радиусы окружности. Т.к. (ON) – медиана, проведенная к основанию, то она также является и высотой, следовательно, (ONperp AB) . 2) Пусть (OQperp AB) . Докажем, что (AN=NB) . Аналогично (triangle AOB) – равнобедренный, (ON) – высота, следовательно, (ON) – медиана. Следовательно, (AN=NB) . Теорема о произведении отрезков хорд Если две хорды окружности пересекаются, то произведение отрезков одной хорды равно произведению отрезков другой хорды. Доказательство Пусть хорды (AB) и (CD) пересекаются в точке (E) . Рассмотрим треугольники (ADE) и (CBE) . В этих треугольниках углы (1) и (2) равны, так как они вписанные и опираются на одну и ту же дугу (BD) , а углы (3) и (4) равны как вертикальные. Треугольники (ADE) и (CBE) подобны (по первому признаку подобия треугольников). Тогда (dfrac = dfrac) , откуда (AEcdot BE = CEcdot DE) . Теорема о касательной и секущей Квадрат отрезка касательной равен произведению секущей на ее внешнюю часть. Доказательство Пусть касательная проходит через точку (M) и касается окружности в точке (A) . Пусть секущая проходит через точку (M) и пересекает окружность в точках (B) и (C) так что (MB . Покажем, что (MBcdot MC = MA^2) . Рассмотрим треугольники (MBA) и (MCA) : (angle M) – общий, (angle BCA = 0,5cdotbuildrelsmileover) . По теореме об угле между касательной и секущей, (angle BAM = 0,5cdotbuildrelsmileover = angle BCA) . Таким образом, треугольники (MBA) и (MCA) подобны по двум углам. Из подобия треугольников (MBA) и (MCA) имеем: (dfrac = dfrac) , что равносильно (MBcdot MC = MA^2) . Следствие Произведение секущей, проведённой из точки (O) , на её внешнюю часть не зависит от выбора секущей, проведённой из точки (O) : Видео:Угол между прямыми в пространстве. Практическая часть. 10 класс.Скачать  Угол между прямыми онлайнС помощью этого онлайн калькулятора можно найти угол между прямыми. Дается подробное решение с пояснениями. Для вычисления угла между прямыми, задайте размерность (2-если рассматривается прямая на плоскости, 3- если рассматривается прямая в пространстве), выберите вид уравнения (канонический, параметрический, общий (для двухмерного пространства)), введите данные в ячейки и нажмите на кнопку «Решить». Теоретическую часть и численные примеры смотрите ниже. ПредупреждениеИнструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д. Видео:21. Угол между прямой и плоскостьюСкачать  1. Угол между прямыми на плоскостиПрямые заданы каноническими уравнениями1.1. Определение угла между прямымиПусть в двухмерном пространстве прямые L1 и L2 заданы каноническими уравнениями
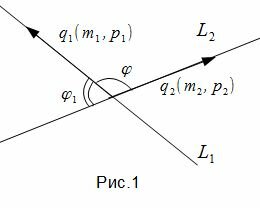
Задача об определении угла между прямыми L1 и L2 сводится к задаче об определении угла между направляющими векторами q1 и q2 (рис.1).
Из выражения (1.3) получим:
Таким образом, из формулы (1.4) можно найти угол между прямыми L1 и L2. Как видно из Рис.1 пересекающиеся прямые образуют смежные углы φ и φ1. Если найденный угол больше 90°, то можно найти минимальный угол между прямыми L1 и L2: φ1=180-φ. Из формулы (1.4) можно вывести условия параллельности и перпендикулярности двух прямых. Пример 1. Определить угол между прямыми
Упростим и решим:
Данный угол больше 90°. Найдем минимальный угол между прямыми. Для этого вычтем этот угол из 180:
Угол между прямыми равен:
1.2. Условие параллельности прямыхПусть φ=0. Тогда cosφ=1. При этом выражение (1.4) примет следующий вид:
Сделаем преобразования с выражением (1.7):
Таким образом условие параллельности прямых L1 и L2 имеет вид (1.8). Если m2≠0 и p2≠0, то (1.8) можно записать так:
Пример 2. Определить, параллельны ли прямые
Удовлетворяется равенство (1.9), следовательно прямые (1.10) и (1.11) параллельны. Ответ. Прямые (1.10) и (1.11) параллельны. 1.3. Условие перпендикулярности прямыхПусть φ=90°. Тогда cosφ=0. При этом выражение (1.4) примет следующий вид:
Правая часть выражения (1.12) равно нулю тогда и только тогда, когда числитель равен нулю. Следовательно, для того, чтобы прямые L1 и L2 были перпендикулярны , должно выполняться условие
Пример 3. Определить, перпендикулярны ли прямые
Удовлетворяется условие (1.13), следовательно прямые (1.14) и (1.15) перпендикулярны. Ответ. Прямые (1.14) и (1.15) перпендикулярны. Прямые заданы общими уравнениями1.4. Определение угла между прямымиПусть две прямые L1 и L2 заданы общими уравнениями
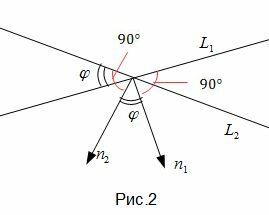
Так как нормальным вектором прямой L1 является n1=(A1, B1), а нормальным вектором прямой L2 является n2=(A2, B2), то задача об определении угла между прямыми L1 и L2 сводится к определению угла φ между векторами n1 и n2 (Рис.2).
Из определения скалярного произведения двух векторов, имеем:
Из уравнения (19) получим
Пример 4. Найти угол между прямыми
Упростим и решим:
Данный угол больше 90°. Найдем минимальный угол между прямыми. Для этого вычтем этот угол из 180:
1.5. Условие параллельности прямыхТак как угол между паралленьными прямыми равен нулю, то φ=0, cos(φ)=1. Тогда сделав преобразования, представленные выше для канонических уравнений прямых получим условие параллельности:
С другой стороны условие параллельности прямых L1 и L2 эквивалентно условию коллинеарности векторов n1 и n2 и можно представить так:
Как видим уравнения (1.24) и (1.25) эквивалентны при A2≠0 и B2≠0. Если в координатах нормальных векторов существует нулевой коэффициент, то нужно использовать уравнение (1.24). Пример 5. Определить, параллельны ли прямые
Удовлетворяется равенство (1.24), следовательно прямые (1.26) и (1.27) параллельны. Ответ. Прямые (1.26) и (1.27) параллельны. 1.6. Условие перпендикулярности прямыхУсловие перпендикулярности прямых L1 и L2 можно извлекать из формулы (1.20), подставляя cos(φ)=0. Тогда скалярное произведение (n1,n2)=0. Откуда
Таким образом условие перпендикулярности прямых определяется равенством (1.28). Пример 6. Определить, перпендикулярны ли прямые
Удовлетворяется равенство (1.28), следовательно прямые (1.29) и (1.30) перпендикулярны. Ответ. Прямые (1.29) и (1.30) перпендикулярны. Видео:10 класс, 21 урок, Угол между прямой и плоскостьюСкачать  2. Угол между прямыми в пространстве2.1. Определение угла между прямымиПусть в пространстве прямые L1 и L2 заданы каноническими уравнениями
Задача об определении угла между прямыми L1 и L2 сводится к задаче об определении угла между направляющими векторами q1 и q2 .
Из выражения (2.3) получим:
Таким образом, из формулы (2.4) можно найти угол между прямыми L1 и L2. Если найденный угол больше 90°, то можно найти минимальный угол между прямыми L1 и L2: φ1=180-φ. Из формулы (2.4) можно вывести условия параллельности и перпендикулярности двух прямых. Пример 1. Определить угол между прямыми
Упростим и решим:
Угол между прямыми равен:
2.2. Условие параллельности прямыхУсловие параллельности прямых эквивалентно условию коллинеарности направляющих векторов q1 и q2, т.е. соответствующие координаты этих векторов пропорциональны. Пусть
где α − некоторое число. Тогда соответствующие координаты векторов q1 и q2 пропорциональны, и, следовательно прямые L1 и L2 параллельны. Условие параллельности прямых можно представить и так:
Отметим, что любую пропорцию Пример 2. Определить, параллельны ли прямые
Удовлетворяется равенство (2.8) (или (2.7)), следовательно прямые (2.9) и (2.10) параллельны. Ответ. Прямые (2,9) и (2,10) параллельны. Пример 3. Определить, параллельны ли прямые
Выражение (2.13) нужно понимать так:
Как мы видим из (2.14) условия (2.13) выполняются. Следовательно прямые (2.11) и (2.12) параллельны. Ответ. Прямые (2.11) и (2.12) параллельны. 2.3. Условие перпендикулярности прямыхПусть φ=90°. Тогда cosφ=0. При этом выражение (2.4) примет следующий вид:
Правая часть выражения (2.15) равно нулю тогда и только тогда, когда числитель равен нулю. Следовательно, для того, чтобы прямые L1 и L2 были перпендикулярны , должно выполняться условие
Пример 3. Определить, перпендикулярны ли прямые
Удовлетворяется условие (2.16), следовательно прямые (2.17) и (2.18) перпендикулярны. Ответ. Прямые (2.17) и (2.18) перпендикулярны. 📸 Видео#27. Как найти угол между прямой и плоскостью? (Стереометрия)Скачать  Как находить угол между векторамиСкачать  Видеоурок "Угол между прямыми"Скачать  Видеоурок "Угол между прямой и плоскостью"Скачать  Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать  ✓ Угол между плоскостями | ЕГЭ-2017. Задание 13. Математика. Профильный уровень | Борис ТрушинСкачать  Сопряжение прямой с окружностьюСкачать  Математика без Ху!ни. Взаимное расположение прямой и плоскости.Скачать  Угол между прямыми в пространстве. 11 класс.Скачать  Как искать точки на тригонометрической окружности.Скачать  Угол между прямыми!Скачать  Окружность. 7 класс.Скачать  |



































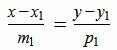 ,
,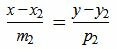 ,
, ,
, ,
,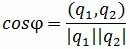
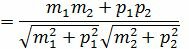 .
.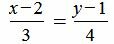 .
.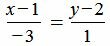 .
.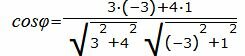 .
.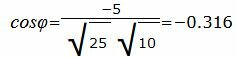 .
.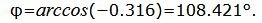

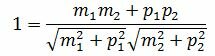 .
.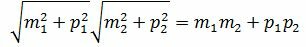 ,
,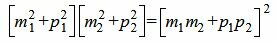 ,
,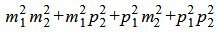
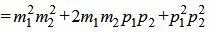 ,
,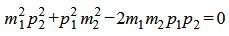 ,
,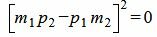 ,
,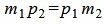 .
.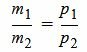 .
.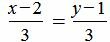 .
.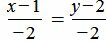 .
.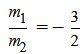 ,
, 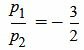 .
.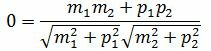 .
.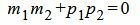 .
.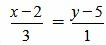
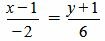 .
.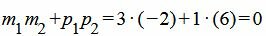 .
.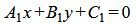
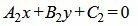 .
. .
.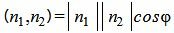 .
.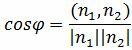
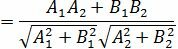 .
.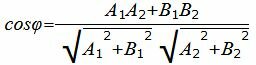
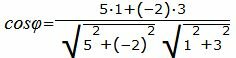
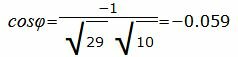
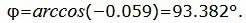
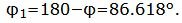
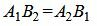 .
.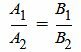 .
.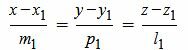 ,
,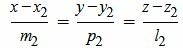 ,
,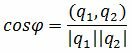
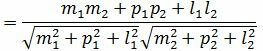 .
.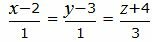 .
.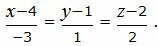
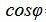
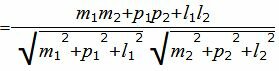 .
.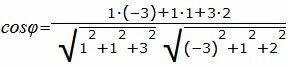 .
.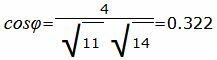 .
.
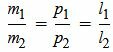
 нужно понимать как равенство ad=bc.
нужно понимать как равенство ad=bc.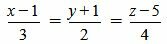 .
.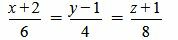 .
.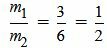 ,
, 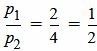 ,
, 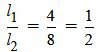 .
.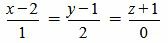 .
.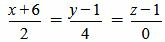 .
.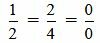 .
.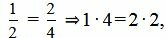 ,
, 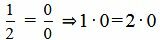 ,
, 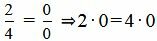 .
.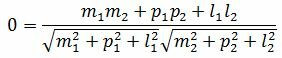 .
.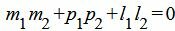 .
.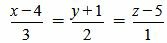
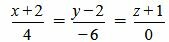 .
.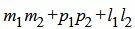
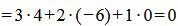 .
.