Цель. Рассмотреть правила разбиения множества на классы, уметь решать задачи на классификацию, освоить математическую символику связанную с этими понятиями.
Теоретическая часть
Вопросы к изучению
1. Понятие разбиения множества на классы.
2. Некоторые задачи, связанные с операциями над конечными множествами.
Ø дихотомическая классификация.
Обозначения
n (A) — число элементов конечного множества А.
Правила
· Разбиения множества на классы;
· Нахождения числа элементов в объединении конечных множеств:
n (А ÈВ) = n (А) + n (В) – n (AÈB);
n (А ÈВ) = n (А) + n (В), если (А Ç B ) = Æ.
Практическая часть
1. Выделите из множества К= два подмножества. В одно включите числа, кратные 2, а в другое – кратные 3. Произошло ли разбиение множества К на класс чисел, кратных 2, и класс чисел, кратных 3? Можно ли разбить данное множество К на три класса: К1= , К2= , К3= ?
2. Определите классы разбиения множества Х четырехугольников, если оно осуществляется при помощи: 1) свойства «быть прямоугольником»; 2) свойств «быть прямоугольником» и «быть ромбом»; 3) свойств «быть прямоугольником» и «быть квадратом»; 4) свойств «быть прямоугольником» и «быть трапецией».
3. Из множества натуральных чисел выделите подмножество чисел, кратных 8. На сколько классов при этом произошло разбиение множества натуральных чисел? Изобразите полученные классы при помощи кругов Эйлера и назовите по два представителя из каждого класса.
4. На какие классы разбивается множество точек плоскости при помощи: а) окружности; б) круга; в) прямой?
5. На множестве натуральных чисел рассматривается свойство «быть кратным 7». Сколько классов разбиения множества N оно определяет? Назовите по два элемента из каждого класса.
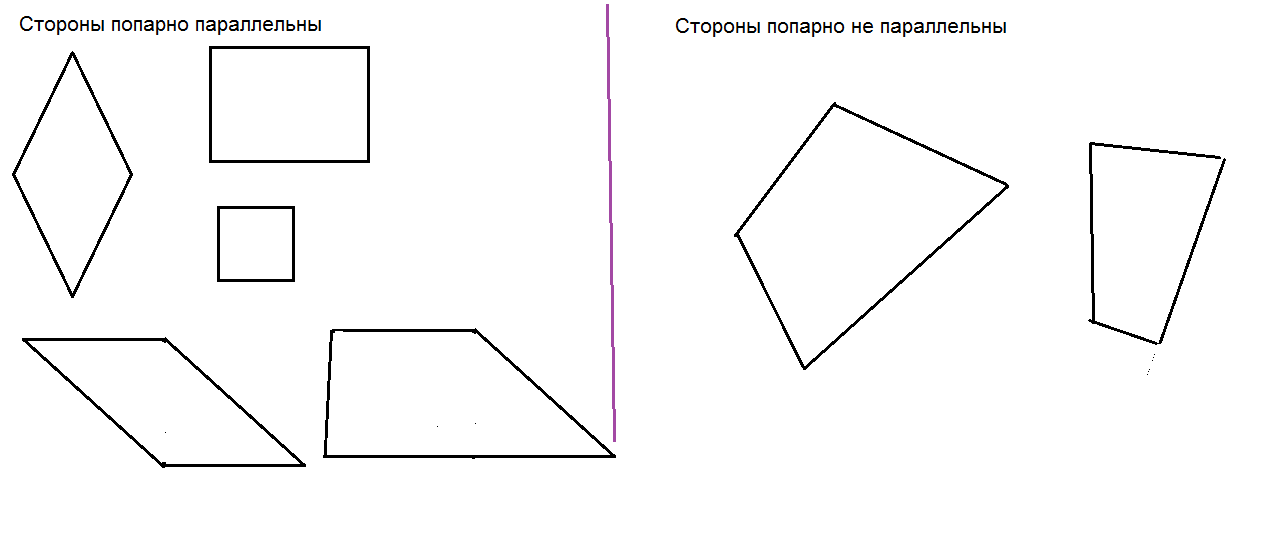
6. Из множества четырехугольников выделили подмножество фигур с попарно параллельными сторонами. На какие классы разбивается множество четырехугольников с помощью свойства «иметь попарно параллельные стороны»? Начертите по два четырехугольника из каждого класса.
7. Изобразите при помощи кругов Эйлера множество N натуральных чисел и его подмножества: четных чисел и чисел кратных 7. Можно ли утверждать, что множество N разбито: а) на два класса: четных чисел и чисел, кратных 7; б) на четыре класса: четных чисел, кратных 7; в) нечетных чисел, не кратных 7; г) четных чисел не кратных 7; д) нечетных чисел, кратных 7.
8. На множестве четырехугольников рассматриваются два свойства: «быть прямоугольником» и «быть квадратом». На какие классы разобьется множество четырехугольников при помощи этих свойств? Начертите по два четырехугольника из каждого класса.
9. Изменится ли ответ в предыдущем упражнении, если на множестве четырехугольников рассмотреть свойства: а) «быть прямоугольником» и «быть ромбом»; б) «быть прямоугольником» и «быть трапецией»?
10. Можно ли узнать, сколько человек в классе, если в нем: 1) 17 мальчиков и 15 девочек; 2) 17 мальчиков и 23 спортсмена?
11. Из 50 учащихся 37 изучают английский язык, 17- немецкий. Сколько человек изучают оба языка?
1. Из 32 школьников 12 занимаются в волейбольной секции, 15 – в баскетбольной, 8 человек занимаются и в той и в другой секции. Сколько школьников не занимаются ни в волейбольной, ни в баскетбольной секции?
2. В делегации 6 человек, знающих французский или немецкий язык. Трое из них говорят только на французском, двое – только на немецком. Сколько человек говорят на двух языках – французском и немецком?
3. Из 100 студентов английский язык изучают 28 человека, немецкий – 30 человек, французский – 42, английский и немецкий – 8, английский и французский – 10, немецкий и французский – 15. Все три языка изучают 3 учащихся. Сколько студентов изучают только один язык? Сколько студентов не изучают ни одного языка?
4. В школе 70 учеников. Из них 27 ходит в драмкружок, 32 поют в хоре, 22 увлекаются спортом. В драмкружке 10 ребят из хора, в хоре 6 спортсменов, в драмкружке 8 спортсменов. 3 спортсмена посещают и драмкружок, и хор. Сколько ребят не поют в хоре, не увлекаются спортом и не ходят в драмкружок?
5. Докажите, что если п – число свойств, с помощью которых множество разбивается на максимальное число классов, то число этих классов равно 2 п
Дата добавления: 2021-01-26 ; просмотров: 280 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Видео:Параллелограмм, прямоугольник, ромб,квадрат,трапеция, все свойства и определения!!!Скачать

По какому одному свойству можно разбить множество четырехугольников
УСЛОВИЕ:
На множестве четырехугольников рассматриваются два свойства: «быть прямоугольником» и «быть ромбом». На какие классы разобьется множество четырехугольников при помощи этих свойств? Начертите по два четырехугольника из каждого класса.
Наверное, на те, у которых стороны попарно параллельны и те, у которых стороны не параллельны.
Вопрос к решению?
Добавил vk190290376, просмотры: ☺ 2117 ⌚ 09.01.2018. математика 1k класс
Решения пользователей
Лучший ответ к заданию выводится как основной
Хочешь предложить свое решение?
Войди и сделай это!
Написать комментарий
y’=11/cos^2(x)-11
y’=(11-11cos^2(x))cos^2(x)=11(1-cos^2(x)/cos^2(x)=11sin^2(x)/cos^2(x)=11tg^2(x)>0
y’>0. Следовательно функция y(x) возрастает на отрезке [-pi/4;pi/4].
Значит, ее наименьшее значение равно y(-pi/4)= 11*tg(-pi/4)-11*(-pi/4)-11*pi/4+12=11*(-1)+11pi/4-11pi/4+12=-11+12=1
Ответ: 1
Если поменять местами x и y, то уравнение [b]не изменится.[/b]
Значит [b] y = x[/b] является решением уравнения и уравнение примет вид:
2y^3+1=y^4+y^2+1 или (2y^3+1)(y^4+y^2+1)=1
y=1 или y^2(y+1)(2y^2+y+1)=0;
а значит x=y=1 или y=-1 не удовлетворяет условию задачи
Проводим перпендикуляр из точки А на прямую ВС_(1) как высоту [i]равнобедренного [/i]треугольника АВС_(1), проведенную на боковую сторону.
Δ АВС_(1) — равнобедренный, так как
АС_(1)=ВС_(1)=sqrt(2) — диагонали боковых граней, которые являются [blue]квадратами.[/blue]
Найдем высоту [b]h[/b] равнобедренного треугольника АВС_(1)
S_( Δ АВС_(1))=(1/2) * AB*h
C другой стороны
S_( Δ АВС_(1))=(1/2) * BС_(1)*AD
Приравниваем правые части:
(1/2) * AB*h=(1/2) * BС_(1)*AD ⇒ AD=AB*h/BC_(1)=(sqrt(7)/2)/sqrt(2)=sqrt(7)/(2sqrt(2))=sqrt(7)*sqrt(2)/(2*2)=[b]sqrt(14)/4[/b]
Проводим АК ⊥ BC
Призма прямая, значит боковые ребра перпендикулярны плоскости АВС, а значит и любой прямой в этой плоскости
Поэтому BB_(1) ⊥ AK
⇒ АК ⊥ ВС и АК ⊥ ВВ_(1)
АК перпендикулярна двум пересекающимся прямым плоскости, значит АК ⊥ пл ВВ_(1)С_(1)С
О т в е т.[b] sqrt(3)/2[/b]
КАРТА – СХЕМА УЧЕБНОГО ЗАНЯТИЯ
продолжительность — 90 минут
Тема занятия: Декартово произведение и разбиение множеств на классы
расширить знания студентов с темы действия с множествами, рассмотреть Декартово произведение, разбиение множеств на классы;
способствовать развитию памяти, внимания, логического мышления;
создать условия для применения полученных знаний при выполнении расчетных заданий.
Необходимое аппаратное и программное обеспечение:
Карточки с заданиями самостоятельной работы
Стойлова АП. Математика : учебник для студ. учреждений высш.образования / Л.П. Стойлова. — 4-е изд., стер. — М. : Издательский центр «Академия», 2014.
Стойлова АП. Математика : учебник для студ. учреждений высш.образования / Л.П. Стойлова. — 4-е изд., стер. — М. : Издательский центр «Академия», 2014.
Тип и вид учебного занятия:
ОРГАНИЗАЦИОННАЯ СТРУКТУРА УРОКА
Содержание и виды деятельности преподавателя
1. Организационный этап
Приветствие, выявление отсутствующих, информирование о теме и целях занятия.
2. Актуализация ЗУН
— Что такое множество? Что означает задать множество?
— Способы задания множеств
— Что такое подмножество?
-какие действия выполняем над множествами?
— Что такое пересечение? Объединение?
— Какие свойства пересечения, объединения?
Самостоятельная работа (с взаимопроверкой)
Найдите: а) А∩В; б) А∩С; в) С∩В.
Найдите: а) АUВ; б) АUС; в) СUВ.
Найдите а)(А∩В)∩С; б) )(АВ)С; в) (А В)∩С
3. Изучение нового материала
— разбиение множеств на классы
4. Первичное закрепление
Практическое выполнение заданий
5. Информация о домашнем задании
Методические рекомендации для самостоятельной работы
6. Подведение итогов урока
Подведение итогов работы группы, отдельных студентов.
Корректирование пробелов знаний.
В начальных классах ученики решают задачу: используя цифры 1, 2, 3 образовать всевозможные двузначные числа.
Путем перебора дети получают:
Запись каждого числа состоит из двух цифр, причем существенен порядок их следования. Например, из цифр 1, 2 образованы числа 12 и 21.
В том случае, когда важен порядок следования элементов множества, в математике говорят об упорядоченных наборах элементов. В данной задаче – упорядоченные пары (а; b), образованные из элементов а и b. Это (1; 2), (1; 3), (1; 4) и т.д. Первый элемент а называют первой координатой пары, элемент b – второй.
Значит, в нашей задаче мы оперировали множеством А=<1, 2, 3> и образовывали всевозможные пары.
Рассмотрим другой пример. Пусть А=, B=. Образуем всевозможные пары (а;b) так, что аА, bВ. Получим некоторое новое множество , элементами которого являются упорядоченные пары чисел. Это новое множество называют декартовым произведением множеств А и В.
Операцию нахождения декартового произведения множеств А и В называют декартовым умножением этих множеств.
Рассмотрим следующий пример. Известно, что АВ= . Установим, из каких элементов состоят множества А и В. Так как первая компонента пары декартового произведения принадлежит множеству А, а вторая – множеству В, то данные множества имеют следующий вид: А=, B= <3, 5,6>.
Перечислим элементы, принадлежащие множеству АВ, если
А= <a, b, c,d>, B=A. Декартово произведение АВ=<(a, a), (a, b), (a, c),
(a, d), (b, a), (b, b), (b, c), (b, d), (c, a), (c, b), (c, c), (c, d), (d, a), (d, b) ,(d, c), (d, d)>.
Количество пар в декартовом прoизведении АВ будет равно произведению числа элементов множества А и числа элементов множества В: n(АВ)=n(A)n(B).
В математике рассматривают не только упорядоченные пары, но и наборы из трех, четырех и т.д. элементов. Такие упорядоченные наборы называют кортежами. Так, набор (1, 5, 6) есть кортеж длины 3, так как в нем три элемента.
Используя понятие кортежа, можно определить понятие декартового произведения n множеств.
Декартовым произведением множеств А, А,…, A называют множество кортежей длины n, образованных так, что первая компонента принадлежит множеству А, вторая – А, …, n-ая – множеству А: АА…A.
Понятие разбиения множества на классы
Понятие множества и операций над множествами позволяют уточнить представление о классификации.
Классификация – это действие распределения объектов по классам на основании сходств внутри класса и их отличия от других объектов. Классификация широко применяется в математике.
Например, натуральные числа делятся на четные и нечетные; углы бывают острые, тупые и прямые и т.д.
Любая классификация связана с разбиением некоторого множества объектов на подмножества.
1) подмножества Х, Х,…, Х попарно не пересекаются;
2) объединение этих подмножеств совпадает с множеством Х.
Если не выполнено хотя бы одно из этих условий, классификацию считают неправильной.
Например: а) Множество треугольников Х разбито на три класса: остроугольные, прямоугольные и тупоугольные. Действительно, выделенные подмножества попарно не пересекаются, а их объединение совпадает с множеством Х; b) Из множества треугольников Х выделили подмножества равнобедренных, равносторонних и разносторонних треугольников. Так как множества равнобедренных и равносторонних треугольников пересекаются, значит, не выполнено первое условие классификации, и разбиения множества Х на классы мы не получили.
Так как разбиение множества на классы связано с выделением его подмножеств, то классификацию можно выполнять при помощи свойств элементов множеств.
Рассмотрим, например, множество натуральных чисел. Его элементы обладают различными свойствами. Нас интересуют числа со свойством «быть кратным 3». Это свойство позволяет выделить из множества N подмножество, состоящее из чисел, кратных 3. Тогда про остальные натуральные числа можно сказать, что они не кратны 3, т.е. получаем еще одно подмножество множества N. Так как выделенные подмножества не пересекаются, а их объединение совпадает с множеством N, то имеем разбиение данного множества на два класса.
Вообще, если на множестве Х задано одно свойство, то это множество разбивается на два класса. Первый – это класс объектов, обладающих данным свойством, а второй – дополнение первого класса до множества Х. Во втором классе содержатся такие объекты множества Х, которые заданным свойством не обладают. Такую классификацию называют дихотомической.
Рассмотрим ситуацию, когда для элементов множества заданы два свойства. Например, свойства натуральных чисел: «быть кратным 3» и «быть кратным 5». При помощи этих свойств из множества N можно выделить два подмножества: А – множество чисел, кратных 3 и В – множество чисел, кратных 5. Эти множества пересекаются, но ни одно из них не является подмножеством другого (рис. 13). Разбиения на подмножества А и В в данном случае на произошло. Но круг, изображающий множество N, можно рассматривать как состоящий из четырех непересекающихся областей. Каждая область изображает некоторое подмножество множество N. Множество I состоит из чисел, кратных 3 и 5, множество I – из чисел, кратных 3 и не кратных 5, множество III – из чисел, кратных 5 и не кратных 3, множество IV – из чисел, не кратных 3 и не кратных 5. Объединение этих четырех множеств есть множество N.
Таким образом, выделение двух свойств привело к разбиению множества N натуральных чисел на четыре класса.
Не следует думать, что задание двух свойств элементов множества всегда приводит к разбиению этого множества на четыре класса. Например, при помощи таких двух свойств «быть кратным 3» и «быть кратным 6» множество натуральных чисел разбивается на три класса (рис. 14): I – класс чисел, кратных 6; II – класс чисел, кратных 3, но не кратных 6; III – класс чисел, не кратных 3.
Примеры
Приведем несколько примеров разбиения:
1. Множество четырехугольников 
трапеции и прямоугольники. Данные подмножества попарно не пересекаются, а их объединения совпадают с множеством 
2. Множество четырехугольников 
квадраты, параллелограммы, прямоугольники. Так как прямоугольник и квадрат – частные случаи параллелограмма, то данные подмножества пересекаются, значит, не выполнено первое условие классификации, и разбиение множества 
3. Дано множество прямых 

4. Дано множество 




5. Множество 












Решение. Элементами множества А1´ А2 ´А3 будут кортежи длины 3 такие, что первая их компонента принадлежит множеству А1, вторая – множеству А2, третья – множеству А3.
Пример 2. Пусть на множестве Х= задано отношение «меньше» (т.е. первый элемент меньше второго, второй меньше третьего). Записать декартово произведение XX. Из этого множества следует выбрать элементы, которые должны удовлетворять отношению «меньше».
Декартово произведение X Х может быть записано в виде множества из упорядоченных пар:
Из этого множества выбираются элементы, которые удовлетворяют отношению «меньше». В результате получится новое множество из упорядоченных пар:
В новом множестве все пары являются элементами декартова произведения XX. Отношение «меньше» на множестве Х является подмножеством декартова произведения XX. Бинарное отношение на множестве Х есть подмножество декартова произведения W XX.
2) Декартово произведение двух множеств X Y.
Пусть заданы два множества: X= , Y= .
Записать декартово произведение X Y .
Декартово произведение двух множеств равно:
Аналогично можно найти декартово произведение трёх множеств: X Y Z.
Цель. Рассмотреть правила разбиения множества на классы, уметь решать задачи на классификацию, освоить математическую символику связанную с этими понятиями. Уметь привести примеры на использование понятия классификации из начального курса математики.
Теоретическая часть
Вопросы к изучению
1. Понятие разбиения множества на классы.
2. Некоторые задачи, связанные с операциями над конечными множествами.
Ø дихотомическая классификация.
Обозначения
n (A) — число элементов конечного множества А.
Правила
· Разбиения множества на классы;
· Нахождения числа элементов в объединении конечных множеств:
n (А ÈВ) = n (А) + n (В) – n (AÈB);
n (А ÈВ) = n (А) + n (В), если (А Ç B ) = Æ.
Практическая часть
1. Выделите из множества К= два подмножества. В одно включите числа, кратные 2, а в другое – кратные 3. Произошло ли разбиение множества К на класс чисел, кратных 2, и класс чисел, кратных 3? Можно ли разбить данное множество К на три класса: К1= , К2= , К3= ?
2. Определите классы разбиения множества Х четырехугольников, если оно осуществляется при помощи: 1) свойства «быть прямоугольником»; 2) свойств «быть прямоугольником» и «быть ромбом»; 3) свойств «быть прямоугольником» и «быть квадратом»; 4) свойств «быть прямоугольником» и «быть трапецией».
3. Из множества натуральных чисел выделите подмножество чисел, кратных 8. На сколько классов при этом произошло разбиение множества натуральных чисел? Изобразите полученные классы при помощи кругов Эйлера и назовите по два представителя из каждого класса.
4. На какие классы разбивается множество точек плоскости при помощи: а) окружности; б) круга; в) прямой?
5. На множестве натуральных чисел рассматривается свойство «быть кратным 7». Сколько классов разбиения множества N оно определяет? Назовите по два элемента из каждого класса.
6. Из множества четырехугольников выделили подмножество фигур с попарно параллельными сторонами. На какие классы разбивается множество четырехугольников с помощью свойства «иметь попарно параллельные стороны»? Начертите по два четырехугольника из каждого класса.
7. Изобразите при помощи кругов Эйлера множество N натуральных чисел и его подмножества: четных чисел и чисел кратных 7. Можно ли утверждать, что множество N разбито: а) на два класса: четных чисел и чисел, кратных 7; б) на четыре класса: четных чисел, кратных 7; в) нечетных чисел, не кратных 7; г) четных чисел не кратных 7; д) нечетных чисел, кратных 7.
8. На множестве четырехугольников рассматриваются два свойства: «быть прямоугольником» и «быть квадратом». На какие классы разобьется множество четырехугольников при помощи этих свойств? Начертите по два четырехугольника из каждого класса.
9. Изменится ли ответ в предыдущем упражнении, если на множестве четырехугольников рассмотреть свойства: а) «быть прямоугольником» и «быть ромбом»; б) «быть прямоугольником» и «быть трапецией»?
10. Можно ли узнать, сколько человек в классе, если в нем: 1) 17 мальчиков и 15 девочек; 2) 17 мальчиков и 23 спортсмена?
11. Из 50 учащихся 37 изучают английский язык, 17- немецкий. Сколько человек изучают оба языка?
1. Придумайте три примера известных вам классификаций из нематематических наук
2. Из 32 школьников 12 занимаются в волейбольной секции, 15 – в баскетбольной, 8 человек занимаются и в той и в другой секции. Сколько школьников не занимаются ни в волейбольной, ни в баскетбольной секции?
3. В делегации 6 человек, знающих французский или немецкий язык. Трое из них говорят только на французском, двое – только на немецком. Сколько человек говорят на двух языках – французском и немецком?
4. Из 100 студентов английский язык изучают 28 человека, немецкий – 30 человек, французский – 42, английский и немецкий – 8, английский и французский – 10, немецкий и французский – 15. Все три языка изучают 3 учащихся. Сколько студентов изучают только один язык? Сколько студентов не изучают ни одного языка?
5. В школе 70 учеников. Из них 27 ходит в драмкружок, 32 поют в хоре, 22 увлекаются спортом. В драмкружке 10 ребят из хора, в хоре 6 спортсменов, в драмкружке 8 спортсменов. 3 спортсмена посещают и драмкружок, и хор. Сколько ребят не поют в хоре, не увлекаются спортом и не ходят в драмкружок?
6. Докажите, что если п – число свойств, с помощью которых множество разбивается на максимальное число классов, то число этих классов равно 2п
ТЕМА 5. ДЕКАРТОВО ПРОИЗВЕДЕНИЕ МНОЖЕСТВ (ЛЕКЦИЯ)
1. Декартово произведение множеств
2. Свойства операции декартова произведения
3. Кортеж. Длина кортежа
ТЕМА 5.1. НЕКОТОРЫЕ ЗАДАЧИ, СВЯЗАННЫЕ С ДЕКАРТОВЫМ ПРОИЗВЕДЕНИЕМ МНОЖЕСТВ (С/Р)
1. Число элементов в объединении и разности конечных множеств
2. Число элементов в декартовом произведении конечных множеств
ПРАКТИЧЕСКАЯ РАБОТА 4. ДЕКАРТОВО ПРОИЗВЕДЕНИЕ
Цель. Уметь решать практические задачи на понятие декартова произведения и его свойств.
Теоретическая часть
Вопросы к изучению
1. Декартово произведение множеств
2. Свойства операции декартова произведения
3. Кортеж. Длина кортежа
Ø декартово произведение множеств;
Ø длина кортежа
Обозначения
А ´ В = — запись определения декартова произведения множеств А и В.
Ø Операции над множествами: объединение, пересечение, вычитание, декартово произведение.
Ø Свойства этих операций:
· дистрибутивность декартова произведения относительно объединения и вычитания множеств, т.е. для любых множеств А, В и С выполняются равенства: (AÈB) ´ С = (A ´ С) È (B ´ С), (A B) ´ С = (A ´ С) (B ´ С).
Правила
Ø Нахождения числа элементов в декартовом произведении конечных множеств: n (А ´ В) = n (А) × n (В).
Практическая часть
1. Элементами множеств А и В являются пары чисел: А = , В = . Найдите пересечение и объединение данных множеств.
2. Запишите различные двузначные числа, используя цифры 3, 4 и 5. Сколько среди них таких, запись которых начинается с цифры 3? Как связано решение данной задачи с понятием декартова произведения множеств?
3. Перечислите элементы декартова произведения A ´ В, если: а) А = , B = ; б) А = В = ; в) А = , В = Æ.
4. Даны множества А = и В = . Перечислите элементы множеств A ´ В и В ´ А. Верно ли, что: а) Множества A ´ В и В ´ А содержат одинаковое число элементов; б) Множества A ´ В и В ´ А равны?
5. Проверьте справедливость равенства (AÈB) ´ С = (A ´ С) È (B ´ С) для множеств А = , В = , С = . Выполняется ли для них равенство (A B) ´ С = (A ´ С) (B ´ С) ?
6. Сколько букв в слове «барабан»? Сколько различных букв в этом слове? Сформулируйте эту задачу, используя понятия множества и кортежа.
7. Чем отличается множество цифр в записи числа 56576 от кортежа цифр в его записи?
8. Изобразите в прямоугольной системе координат множество A ´ В, если: а) А = [-2; 2]. В = ; б) А = [-2; 2]. В = (2, 4); в) А = R, В = [2; 4].
1. Изобразите на декартовой плоскости множество [ 0; 1) ´ (0,1); ´ [ 0; 1); [ 0; 1) ´ R; N ´ R; N ´ ; ´ N; ´ R.
2. В звене 7 мальчиков и 6 девочек. Сколькими способами можно выбрать пару учеников, состоящую из мальчика и девочки, для дежурства по классу?
3. В каких случаях А´В = В´А?
4. Составьте таблицу результатов однокругового шахматного турнира трех: Иванова, Петрова, Сидорова (результаты возьмите произвольно).
5. Фабрика верхнего трикотажа изготовляет мужские пуловеры, женские костюмы, кофты и платья следующих расцветок: бордовая, синяя, голубая, зеленая, коричневая, серая. Составьте таблицу, иллюстрирующую декартово произведение множества изделий и множества цветов, и заполните ее.
6. Решите следующие задачи, построив дерево возможных вариантов: А) у продавца имеется три варианта мороженного: клубничное, сливочное и ореховое. Наташа и Катя решили купить по одной порции. Сколько существует вариантов такой покупки? Б) Туристическая фирма планирует посещение туристами в Италии трех городов: Венеции, Рима и Флоренции. Сколько существует вариантов такого маршрута?
Видео:Как решить любую задачу с четырёхугольниками? | Математика TutorOnlineСкачать

Понятие разбиения множества на классы
Понятия множества и операций над множествами позволяют уточнить наше представление о классификации — действии распределения объектов по классам.
Классификацию мы выполняем достаточно часто. Так, натуральные числа представляем как два класса — четные и нечетные. Углы на плоскости разбиваем на три класса: прямые, острые и тупые.
Любая классификация связана с разбиением некоторого множества объектов на подмножества. При этом считают, что множество X разбито на классы X1, Х2. Хn . если:
1) подмножества Х1, Х2. Хп. попарно не пересекаются; |
2) объединение подмножеств X1, Х2, . Хn, . совпадает с множеством X. |
Если не выполнено хотя бы одно из условий, классификацию считают неправильной. Например, если из множества X треугольников выделить подмножества равнобедренных, равно-сторонних и разносторонних треугольников, то разбиения мы не получим, поскольку подмно-жества равнобедренных и равносторонних треугольников пересекаются (все равносторонние треугольники являются равнобедренными). В данном случае не выполнено первое условие разбиения множества на классы.
Так как разбиение множества на классы связано с выделением его подмножеств, то классификацию можно выполнять при помощи свойств элементов множеств.
Рассмотрим, например, множество натуральных чисел. Его элементы обладают различными свойствами. Положим, что нас интересуют числа, обладающие свойством «быть кратным 3». Это свойство позволяет выделить из множества натуральных чисел подмножество, состоящее из чисел, кратных 3. Тогда про остальные натуральные числа можно сказать, что они не кратны 3, т.е. получаем еще одно подмножество
множества натуральных чисел (рис. 12). Так как выделенные подмножества не пересекаются, а их объединение совпадает с множеством натуральных чисел, то имеем разбиение этого множества на два класса.
 |  |
| Рис. 12 | Рис. 13 |
Вообще, если на множестве X задано одно свойство, то это множество разбивается на два класса. Первый — это класс объектов, обладающих этим свойством, а второй — дополнение первого класса до множества X. Во втором классе содержатся такие объекты множества X, которые заданным свойством не обладают. Такую классификацию называют дихотомической.
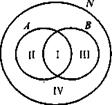
Рассмотрим теперь ситуацию, когда для элементов множества заданы два свойства. Например, такие свойства натуральных чисел, как «быть кратным 3» и «быть кратным 5». При помощи этих свойств из множества N натуральных чисел можно выделить два подмножества: А — подмножество чисел, кратных 3, и В — подмножество чисел, кратных 5. Эти множества пересекаются, но ни одно из них не является подмножеством другого (рис. 13). Проанализируем получившийся рисунок. Конечно, разбиения множества натуральных чисел на подмножества А и В не произошло. Но круг, изображающий множество N, можно рассматривать как состоящий из четырех непересекающихся областей — на рисунке они пронумерованы. Каждая область изображает некоторое подмножество множества N. Подмножество I состоит из чисел, кратных 3 и 5; подмножество II — из чисел, кратных 3 и не кратных 5; подмножество III — из чисел, кратных 5 и не кратных 3; подмножество IV — из чисел, не кратных 3 и не кратных 5. Объединение этих четырех подмножеств есть множество N.
| Не следует думать, что задание двух свойств элементов множества всегда приводит к разбиению этого множества на четыре класса. Например, при помощи таких двух свойств «быть кратным 3» и «быть кратным 6» множество натуральных чисел разбивается на три класса (рис. 14): I -класс чисел, кратных 6; II — класс чисел, кратных 3, но не кратных 6; III — класс чисел, не кратных 3. | 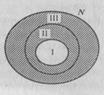 Рис. 14 Рис. 14 |
Таким образом, выделение двух свойств привело к разбиению множества N натуральных чисел на четыре класса.
Упражнения
1. Из множества X = выделили подмножества X,, Х2 и Х3. В каком из следующих случаев множество Х оказалось разбитым на классы:
2. Из множества Х= выделим подмножества:
а) А — четных чисел, В — нечетных чисел;
б) А — чисел, кратных 2; В — чисел, кратных 3; С- чисел, кратных 4;
в) А — нечетных однозначных чисел; В — четных двузначных чисел. В каком случае произошло разбиение множества Х на классы?
3. Из множества треугольников выделили подмножества треугольников:
а) прямоугольные, равнобедренные, равносторонние;
б) остроугольные, тупоугольные, прямоугольные;
в) равносторонние, прямоугольные, тупоугольные.
В каком случае произошло разбиение множества треугольников на классы?
4.На какие классы разбивается множество точек плоскости при помощи:
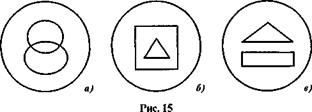
5.Перечертите комбинации фигур, приведенные на рисунке 15, и на каждой из них выделите (различными видами штриховки) непересекающиеся области.
6.На множестве натуральных чисел рассматривается свойство «быть кратным 7». Сколько классов разбиения множества N оно определяет? Назовите по два элемента из каждого класса.
7.Из множества четырехугольников выделили подмножество фигур с попарно параллельными сторонами. На какие классы разбивается множество четырехугольников с помощью свойства «иметь попарно параллельные стороны»? Начертите по два четырехугольника из каждого класса.
8. Изобразите при помощи кругов Эйлера множество N натуральных чисел и его подмножества: четных чисел и чисел, кратных 7. Можно ли утверждать, что множество N разбито:
а) на два класса: четных чисел и чисел, кратных 7;
б) на четыре класса: четных чисел, кратных 7; четных чисел, не кратных 7; нечетных чисел, кратных 7; нечетных чисел, не кратных 7?
9. На множестве четырехугольников рассматриваются два свойства: «быть прямоугольником» и «быть квадратом». На какие классы разобьется множество четырехугольников при помощи этих свойств? Начертите по два четырехугольника из каждого класса.
10. Изменится ли ответ в упражнении 9, если на множестве четырехугольников рассмотреть свойства:
а) «быть прямоугольником» и «быть ромбом»;
б) «быть прямоугольником» и «быть трапецией»?
| 11. На рисунке 16 изображены множество X-студентов группы, А — множество спортсменов этой группы, В — множество отличников этой группы. а) Укажите классы разбиения множества X,полученные с помощью свойств «быть спортсменом» и «быть отличником», и охарактеризуйте каждый из них. б) Сколько получилось бы классов разбиения, если бы ни один отличник группы не был спортсменом? | 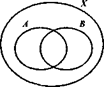 Рис 16 Рис 16 |
11. На рисунке 16 изображены множество X-студентов группы, А — множество спортсменов этой группы, В — множество отличников этой группы.
а) Укажите классы разбиения множества X,полученные с помощью свойств «быть спортсменом» и «быть отличником», и охарактеризуйте каждый из них.
б) Сколько получилось бы классов разбиения, если бы ни один отличник группы не был спортсменом?
Выполните соответствующий рисунок и назовите классы разбиения.
12. Покажите, что решение нижеприведенных задач связано с разбиением заданного множества на классы:
а) 18 редисок связали в пучки по 6 редисок в каждом. Сколько получилось пучков?
б) 18 карандашей раздали 6 ученикам поровну. Сколько карандашей у каждого?
13. О каких множествах и операциях над ними идет речь в задачах:
а) С одной грядки сняли 25 кочанов капусты, а с другой — 15 кочанов. Всю эту капусту разложили в корзины, по 8 кочанов в каждую. Сколько потребовалось корзин?
б) Для школьного сада привезли 24 саженца яблонь. На одном участке посадили 6 саженцев, а на другом — остальные, в 3 ряда поровну. Сколько саженцев посадили в каждом ряду?
Не нашли, что искали? Воспользуйтесь поиском:
🔍 Видео
Математика 2 класс (Урок№43 - Свойство противоположных сторон прямоугольника.)Скачать

А.5.3 Четырехугольники (+ Д/З)Скачать

Четырехугольники. Вебинар | МатематикаСкачать

#58. Олимпиадная задача о четырехугольникеСкачать

3 правила для вписанного четырехугольника #shortsСкачать

Симедиана. Гармонические четырехугольники. | Олимпиадная математикаСкачать

СЛОЖИТЕ ДВА КОРНЯСкачать

Четырехугольники, вписанные в окружность. 9 класс.Скачать

✓ Логарифмическая и степенная функции | матан #027 | Борис ТрушинСкачать

Диагонали четырехугольника равны 4 и 5.Скачать

Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

Математика это не ИсламСкачать

14.10 Переместительное и сочетательное свойства объединения и пересечения множествСкачать

Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать

Урок 6. Треугольники, четырёхугольники, многоугольники. ОГЭ. Вебинар | МатематикаСкачать

Геометрия 8. Урок 13 - Площадь четырехугольников. ЗадачиСкачать

КАК РЕШАТЬ ЗАДАЧИ ПО ГЕОМЕТРИИ? | МатематикаСкачать

Удалили с экзамена ОГЭ Устное Собеседование shorts #shortsСкачать