Какие углы у школьного треугольника

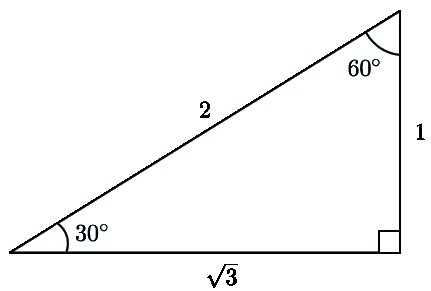
Самый простой многоугольник, который изучается в школе — это треугольник. Он более понятен для учащихся и встречает меньше трудностей. Несмотря на то что существуют различные виды треугольников, у которых имеются особенные свойства.

Видео:Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

Какая фигура называется треугольником?

Образованная тремя точками и отрезками. Первые называются вершинами, вторые — сторонами. Причем все три отрезка должны быть соединены, чтобы между ними образовывались углы. Отсюда и название фигуры «треугольник».

Видео:Что такое угол? Виды углов: прямой, острый, тупой, развернутый уголСкачать

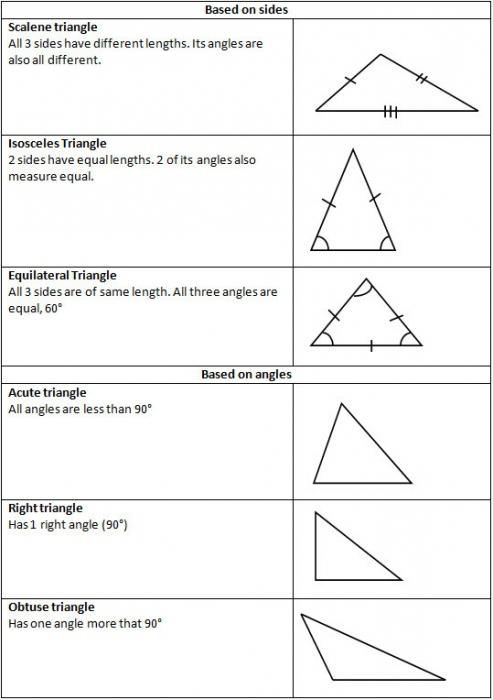
Различия в названиях по углам

Поскольку они могут быть острыми, тупыми и прямыми, то и виды треугольников определяются по этим названиям. Соответственно, групп таких фигур три.

• Первая. Если все углы треугольника острые, то он будет иметь название остроугольного. Все логично.

• Вторая. Один из углов тупой, значит треугольник тупоугольный. Проще некуда.

• Третья. Имеется угол, равный 90 градусам, который называется прямым. Треугольник становится прямоугольным.

Видео:Сумма углов треугольника. Геометрия 7 класс | МатематикаСкачать

Различия в названиях по сторонам

В зависимости от особенностей сторон выделяют такие виды треугольников:

общий случай — разносторонний, в котором все стороны имеют произвольную длину;

равнобедренный, у двух сторон которого имеются одинаковые числовые значения;

равносторонний, длины всех его сторон одинаковые.

Если в задаче не указан конкретный вид треугольника, то нужно чертить произвольный. У которого все углы острые, а стороны имеют разную длину.

Видео:Геометрия за 6 минут — Сумма углов треугольника и Внешний УголСкачать

Свойства, общие для всех треугольников

1. Если сложить все углы треугольника, то получится число, равное 180º. И неважно, какого он вида. Это правило действует всегда.
2. Числовое значение любой стороны треугольника меньше, чем сложенные вместе две другие. При этом она же больше, чем их разность.
3. Каждый внешний угол имеет значение, которое получается при сложении двух внутренних, не смежных с ним. Причем он всегда больше, чем смежный с ним внутренний.
4. Напротив меньшей стороны треугольника всегда лежит самый маленький угол. И наоборот, если сторона большая, то и угол будет самым большим.

Эти свойства справедливы всегда, какие бы виды треугольников ни рассматривались в задачах. Все остальные вытекают из конкретных особенностей.

Видео:Математика | Соотношения между сторонами и углами в прямоугольном треугольнике.Скачать

Свойства равнобедренного треугольника

• Углы, которые прилегают к основанию, равны.
• Высота, которая проведена к основанию, является также медианой и биссектрисой.
• Высоты, медианы и биссектрисы, которые построены к боковым сторонам треугольника, соответственно равны друг другу.

Видео:Математика 3 класс. Виды треугольниковСкачать

Свойства равностороннего треугольника

Если имеется такая фигура, то будут верны все свойства, описанные немного выше. Потому что равносторонний всегда будет равнобедренным. Но не наоборот, равнобедренный треугольник не обязательно будет равносторонним.

• Все его углы равны друг другу и имеют значение 60º.
• Любая медиана равностороннего треугольника является его высотой и биссектрисой. Причем они все равны друг другу. Для определения их значений существует формула, которая состоит из произведения стороны на квадратный корень из 3, деленного на 2.

Видео:Признаки равенства треугольников | теорема пифагора | Математика | TutorOnlineСкачать

Свойства прямоугольного треугольника

• Два острых угла дают в сумме значение в 90º.
• Длина гипотенузы всегда больше, чем у любого из катетов.
• Числовое значение медианы, проведенной к гипотенузе, равно ее половине.
• Этому же значению равен катет, если он лежит напротив угла в 30º.
• Высота, которая проведена из вершины со значением 90º, имеет определенную математическую зависимость от катетов: 1/н 2 = 1/а 2 + 1/в 2 . Здесь: а, в — катеты, н — высота.

Видео:7 класс, 31 урок, Теорема о сумме углов треугольникаСкачать

Задачи с разными видами треугольников

№1. Дан равнобедренный треугольник. Его периметр известен и равен 90 см. Требуется узнать его стороны. В качестве дополнительного условия: боковая сторона меньше основания в 1,2 раза.

Значение периметра напрямую зависит от тех величин, которые нужно найти. Сумма всех трех сторон и даст 90 см. Теперь нужно вспомнить признак треугольника, по которому он является равнобедренным. То есть две стороны равны. Можно составить уравнение с двумя неизвестными: 2а + в = 90. Здесь а — боковая сторона, в — основание.

Настала очередь дополнительного условия. Следуя ему, получается второе уравнение: в = 1,2а. Можно выполнить подстановку этого выражения в первое. Получится: 2а + 1,2а = 90. После преобразований: 3,2а = 90. Отсюда а = 28,125 (см). Теперь несложно узнать основание. Лучше всего это сделать из второго условия: в = 1,2 * 28,125 = 33,75 (см).

Для проверки можно сложить три значения: 28,125 * 2 + 33,75 = 90 (см). Все верно.

Ответ: стороны треугольника равны 28,125 см, 28,125 см, 33,75 см.

№2. Сторона равностороннего треугольника равна 12 см. Нужно вычислить его высоту.

Решение. Для поиска ответа достаточно вернуться к тому моменту, где были описаны свойства треугольника. Так указана формула для нахождения высоты, медианы и биссектрисы равностороннего треугольника.

н = а * √3 / 2, где н — высота, а — сторона.

Подстановка и вычисление дают такой результат: н = 6 √3 (см).

Эту формулу необязательно запоминать. Достаточно вспомнить, что высота делит треугольник на два прямоугольных. Причем она оказывается катетом, а гипотенуза в нем — это сторона исходного, второй катет — половина известной стороны. Теперь нужно записать теорему Пифагора и вывести формулу для высоты.

Ответ: высота равна 6 √3 см.

№3. Дан МКР — треугольник, 90 градусов в котором составляет угол К. Известны стороны МР и КР, они равны соответственно 30 и 15 см. Нужно узнать значение угла Р.

Решение. Если сделать чертеж, то становится ясно, что МР — гипотенуза. Причем она в два раза больше катета КР. Снова нужно обратиться к свойствам. Одно из них как раз связано с углами. Из него понятно, что угол КМР равен 30º. Значит искомый угол Р будет равен 60º. Это следует из другого свойства, которое утверждает, что сумма двух острых углов должна равняться 90º.

Ответ: угол Р равен 60º.

№4. Нужно найти все углы равнобедренного треугольника. Про него известно, что внешний угол от угла при основании равен 110º.

Решение. Поскольку дан только внешний угол, то этим и нужно воспользоваться. Он образует с внутренним углом развернутый. Значит в сумме они дадут 180º. То есть угол при основании треугольника будет равен 70º. Так как он равнобедренный, то второй угол имеет такое же значение. Осталось вычислить третий угол. По свойству, общему для всех треугольников, сумма углов равна 180º. Значит, третий определится как 180º — 70º — 70º = 40º.

Ответ: углы равны 70º, 70º, 40º.

№5. Известно, что в равнобедренном треугольнике угол, лежащий напротив основания, равен 90º. На основании отмечена точка. Отрезок, соединяющий ее с прямым углом, делит его в отношении 1 к 4. Нужно узнать все углы меньшего треугольника.

Решение. Один из углов можно определить сразу. Поскольку треугольник прямоугольный и равнобедренный, то те, что лежат у его основания, будут по 45º, то есть по 90º/2.

Второй из них поможет найти известное в условии отношение. Поскольку оно равно 1 к 4, то частей, на которые он делится получается всего 5. Значит, чтобы узнать меньший угол треугольника нужно 90º/5 = 18º. Осталось узнать третий. Для этого из 180º (суммы всех углов треугольника) нужно вычесть 45º и 18º. Вычисления несложные, и получится: 117º.

Видео:Равнобедренный треугольник. Свойства равнобедренного треугольника | Математика | TutorOnlineСкачать

Виды треугольников

Треугольники бывают остроугольными, тупоугольными, прямоугольными, разносторонними, равносторонними, равнобедренными.

Определение 1. Треугольник называется остроугольным, если все ее углы острые, т.е. меньше 90° (Рис.1).

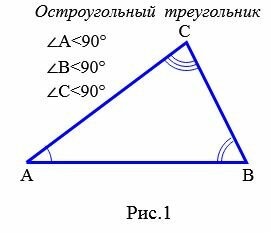Определение 2. Треугольник называется тупоугольным, если один из его углов тупой, т.е. больше 90° (Рис.2).

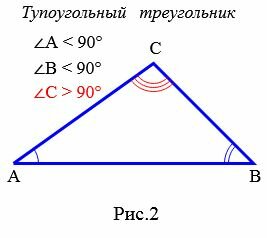Если треугольник тупоугольный, то исходя из того, что сумма всех углов треугольника равна 180°, остальные два угла треугольника будут острыми.

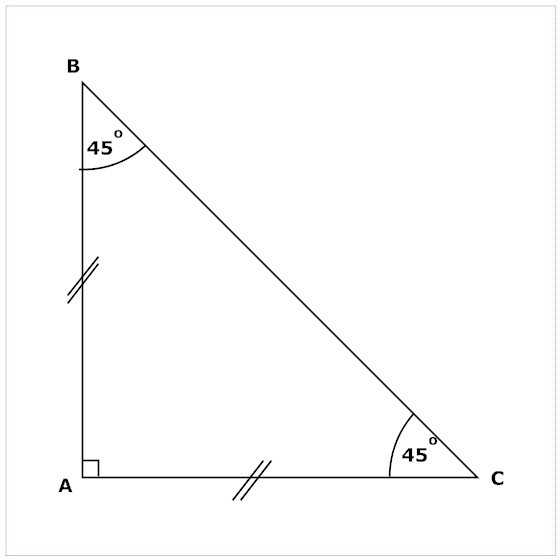
Определение 3. Треугольник называется прямоугольным, если один из его углов прямой, т.е. равен 90° (Рис.3).

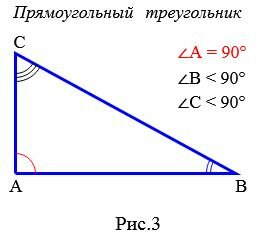Если треугольник прямоугольный, то исходя из того, что сумма всех углов треугольника равна 180°, остальные два угла треугольника будут острыми.

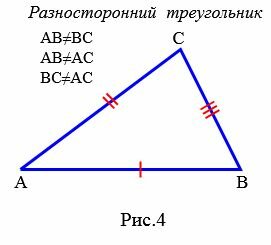
Определение 4. Треугольник называется разносторонним, если длины всех сторон треугольника разные (Рис.4).

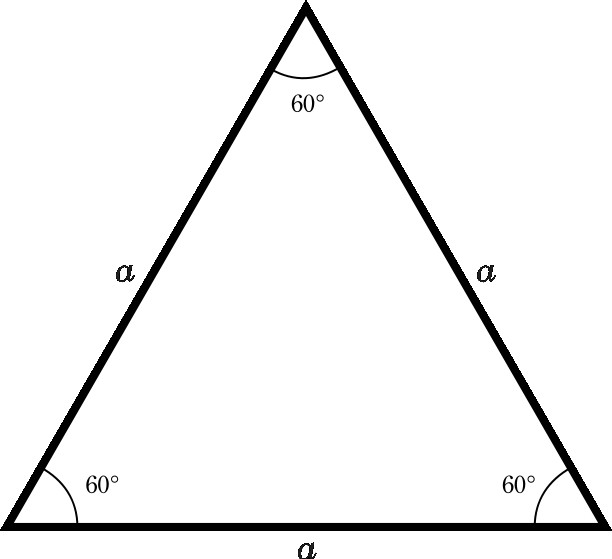
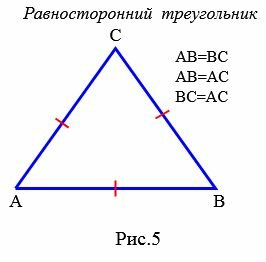
Определение 5. Треугольник называется равносторонним или правильным, если длины всех сторон равны (Рис.5).

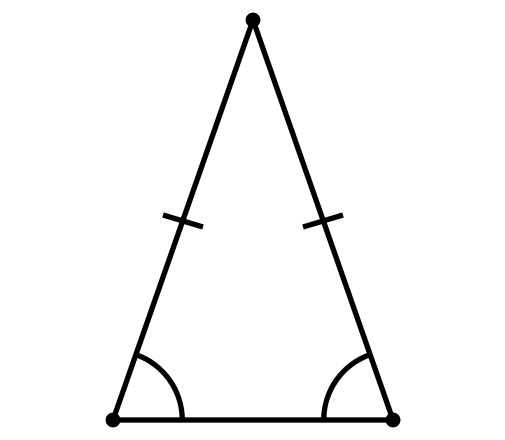
Определение 6. Треугольник называется равнобедренным, если длины двух сторон равны (Рис.6).

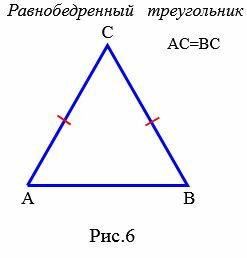В равнобедренном треугольнике равные стороны называются боковыми сторонами треугольника, а третья сторона называется основанием.

Видео:Высшая математика в втузов. Пределы и производныеСкачать

Виды треугольников

Треугольники различаются между собой по характеру углов и по характеру сторон.

Видео:Сравнение углов. Виды углов. Чертежный треугольник. 5 класс.Скачать

Виды треугольников по углам

1. Остроугольный треугольник – это треугольник, у которого все углы острые, то есть меньше 90°.
2. Прямоугольный треугольник – это треугольник, у которого один из углов является прямым, то есть равен 90°.

Стороны, образующие прямой угол называются катетами, а сторона, лежащая напротив прямого угла, называется гипотенузой.

Видео:Построение треугольника по стороне и двум прилежащим к ней углам. 7 класс. Геометрия.Скачать

Виды треугольников по сторонам

1. Разносторонний треугольник – это треугольник, у которого все стороны имеют разную длину.
2. Равнобедренный треугольник – это треугольник, у которого две стороны равны между собой.

Равные стороны называются боковыми сторона треугольника, а третья сторона, не равная двум другим, называется его основанием.

📹 Видео

Все про прямоугольный треугольник. Решаем задачи | Математика | TutorOnlineСкачать

Решали пол-урока, а оказалось очень простоСкачать

Внешний угол треугольникаСкачать

Параллельные прямые | Математика | TutorOnlineСкачать

Только 1 может решить эту хитрую задачу ★ Найдите углы треугольника ★ Супер ЖЕСТЬСкачать

Признаки равенства треугольников. 7 класс.Скачать

Треугольники. 7 класс.Скачать

Советская олимпиада, которую сегодня решить только 2 школьниковСкачать