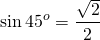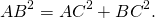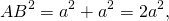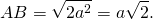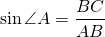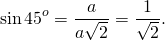Синус — это отношение противолежащего катета к гипотенузе.
Видео:Синус, косинус, тангенс, котангенс за 5 МИНУТСкачать

Синус 30 градусов
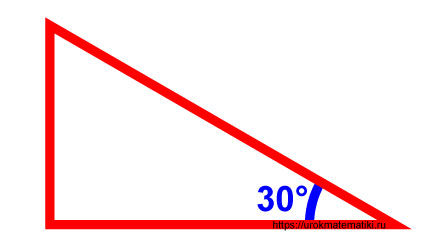
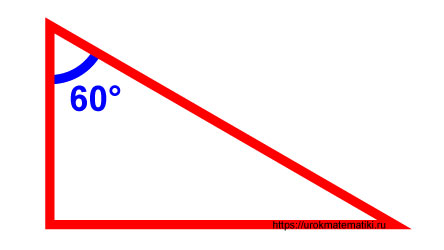
Необходимо найти синус 30 градусов.
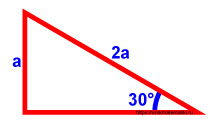
Напротив угла 30° находится катет, обозначим его как a .
В этом случае гипотенуза в два раза больше, так как катет, лежащий против угла 30° равен половине гипотенузы.
sin 30° = a 2 a = 1 2
Итак, sin 30° = 1 2
Видео:ЗНАЧЕНИЯ СИНУСА, КОСИНУСА И ТАНГЕНСА 30, 45 И 60 ГРАДУСОВСкачать
Синус 45 градусов
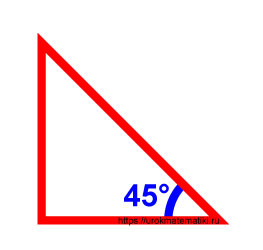
Необходимо найти синус 45 градусов.
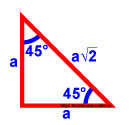
Если в прямоугольном треугольнике один угол равен 45°, то другой угол тоже равен 45° — получается равнобедренный треугольник. Обозначим стороны как a .
Синус — это отношение противолежащего катета к гипотенузе, но гипотенуза не известна. Найдём её по теореме Пифагора: сумма квадратов катетов, затем извлекаем корень.
sin 45° = a a 2 = 1 2
Избавляемся от иррациональности, умножим числитель и знаменатель на 2 .
Итак, sin 45° = 2 2 — табличное значение.
Видео:ТЕОРЕМА СИНУСОВ И ТЕОРЕМА КОСИНУСОВ. Тригонометрия | МатематикаСкачать

Синус 60 градусов
Необходимо найти синус 60 градусов.
Для этого рассмотрим треугольник из первого случая.
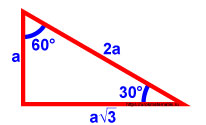
Так гипотенуза равна 2 a , а известный катет принят как a .
По теореме Пифагора можно найти катет, лежащий против угла 60°.
4 a 2 — a 2 = 3 a 2 = a 3
Находим синус 60° — отношение противолежащего катета к гипотенузе:
Видео:Нахождение стороны прямоугольного треугольникаСкачать

Синус, косинус, тангенс угла 45 градусов (sin 45, cos 45, tg 45)
Табличные значения синуса 45, косинуса 45 и тангенса 45 градусов указаны ниже. Далее по тексту следует пояснение метода и правильности вычисления этих значений для произвольного прямоугольного треугольника.
45 градусов — это π/4 радиан. Формулы для значений косинуса, синуса и тангенса пи/4 радиан указаны ниже (хотя они и тождественны).
То есть, например, tg π/4 = tg 45 градусов
Видео:Свойства прямоугольного треугольника. 7 класс.Скачать

ЗНАЧЕНИЯ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ ПРИ α=45°
Как самостоятельно вычислить значения sin cos tg 45 градусов?
Построим и рассмотрим прямоугольный треугольник АВС у которого угол ∠В = 45°. На основании соотношения его сторон, вычислим значения тригонометрических функций в прямоугольном треугольнике для угла 45 градусов. Поскольку треугольник прямоугольный, то значения функций синуса, косинуса и тангенса будут равны соотношению его соответствующих сторон.
Поскольку значение функций синуса, косинуса и тангенса зависят исключительно от градусной меры угла (или значения, выраженного в радианах), то найденные нами соотношения и будут значениями функции синуса 45, косинуса 45 и тангенса 45 градусов.
Согласно свойствам прямоугольного треугольника, угол С — прямой и равен 90 градусам. Угол B мы изначально построили с градусной мерой 45 градусов. Найдем значение угла А. Так как сумма углов треугольника равна 180 градусам, то
∠А + ∠В + ∠С = 180°
Угол C прямой и равен 90 градусам, угол B мы изначально определили как 45 градусов, таким образом:
∠А = 180° —∠С — ∠В = 180° — 90° — 45° = 45°
Поскольку у данного треугольника два угла равны между собой, то треугольник АВС – прямоугольный, и, одновременно, равнобедренный, в котором оба катета равны между собой: AC = BC.
Допустим, что длина сторон равна некому числу АС = ВС = а. Зная длины катетов, вычислим длину гипотенузы.
По теореме Пифагора: АВ 2 =АС 2 +ВС 2
Заменим длины AC и BC на переменную а, тогда получим:
АВ 2 = а 2 + а 2 = 2а 2 ,
В результате мы выразили длины всех сторон прямоугольного треугольника с углом 45 градусов через переменную а.
Согласно свойств тригонометрических функций в прямоугольном треугольнике соотношение соответствующих сторон треугольника будет равным значению соответствующих функций. Таким образом для угла α = 45 градусов:
sin α = BC / AB (согласно определению синуса для прямоугольного треугольника — это отношение противолежащего катета к гипотенузе, BC — катет, AB — гипотенуза)
cos α = AC / AB (согласно определению косинуса — это отношение прилежащего катета к гипотенузе, AC — катет, AB — гипотенуза)
tg α = BC / AC (аналогично, тангенс для угла α будет равен отношению противолежащего катета к прилежащему)
Вместо обозначений сторон подставим значения их длин через переменную а.
Исходя из этого (см. таблицу значений sin 45, cos 45, tg 45) получаем:
Табличные значения sin 45, cos 45, tg 45 (то есть значение синуса 45, косинуса 45 и тангенса 45 градусов можно вычислить как соотношение соответствующих сторон данного треугольника), подставим вычисленные выше значения длин сторон в формулы и получим результат на картинке ниже.
Видео:Решение прямоугольных треугольников. Практическая часть. 8 класс.Скачать

Табличные значения: синус 45, косинус 45 и тангенс 45 градусов
Таким образом:
- тангенс 45 градусов равен единице
- синус 45 градусов равен косинусу 45 градусов и равен корню из двух пополам (то же самое, что и единица, деленная на корень из двух)
Видео:ТРИГОНОМЕТРИЯ | Синус, Косинус, Тангенс, КотангенсСкачать

Синус, косинус и тангенс угла π/4 радиан
- тангенс π/4 ( пи на четыре) равен единице
- синус π/4 ( пи на четыре) градусов равен косинусу π/4 градусов и равен корню из двух пополам
Примечание. В поисковых запросах часто встречается нечто типа «тангенс р/4 или p/4». Это неграмотно. Используйте запрос, например «тангенс пи/4».
Видео:Решение прямоугольных треугольниковСкачать

Синус 45 градусов
Угол 45 градусов в геометрических задачах — один из самых часто встречающихся.
Соответственно, регулярно приходится использовать значения синуса, косинуса, тангенса и котангенса для этого угла.
Найдем, чему равен синус 45 градусов.
Рассмотрим прямоугольный треугольник ABC с острым углом 45 градусов:
Так как два угла треугольника равны: ∠ A= ∠ B, то треугольник ABC — равнобедренный с основанием AB.
По теореме Пифагора
Пусть AC=BC=a, тогда
По определению синуса острого угла прямоугольного треугольника:
Поскольку иррациональность в знаменателе оставлять не принято, и числитель, и знаменатель дроби умножаем на квадратный корень из двух:
🎥 Видео
8 класс, 29 урок, Синус, косинус и тангенс острого угла прямоугольного треугольникаСкачать

ЗАБЫЛ sin(45), cos(30)! КАК получить их из прямоугольного треугольника?Скачать

8 класс, 30 урок, Значения синуса, косинуса и тангенса для углов 30◦, 45◦ и 60◦Скачать

Все про прямоугольный треугольник. Решаем задачи | Математика | TutorOnlineСкачать

ТРИГОНОМЕТРИЯ с нуля — Синус, косинус, тангенс и котангенс острого углаСкачать

Чему равен sin45 и как вывести это значение?Скачать

Геометрия 8. Урок 11- Синус, Косинус, Тангенс и Котангенс угла в прямоугольном треугольнике.Скачать

Высота прямоугольного треугольникаСкачать

Решение прямоугольных треугольников | Алгебра 10 класс #16 | ИнфоурокСкачать

7 класс, 36 урок, Признаки равенства прямоугольных треугольниковСкачать

Тригонометрия: Как запомнить? + ПОЛУЧИ ПОДАРОК от Ольги АлександровныСкачать