Могут ли прямые а и б быть параллельными проекциями параллельных прямых

Геометрия | 10 — 11 классы

1. Прямые a и b лежат в параллельных плоскостях α и β.

Могут ли эти прямые быть : а) параллельными ; б) скрещивающимися?

Сделайте рисунок для каждого возможного случая.

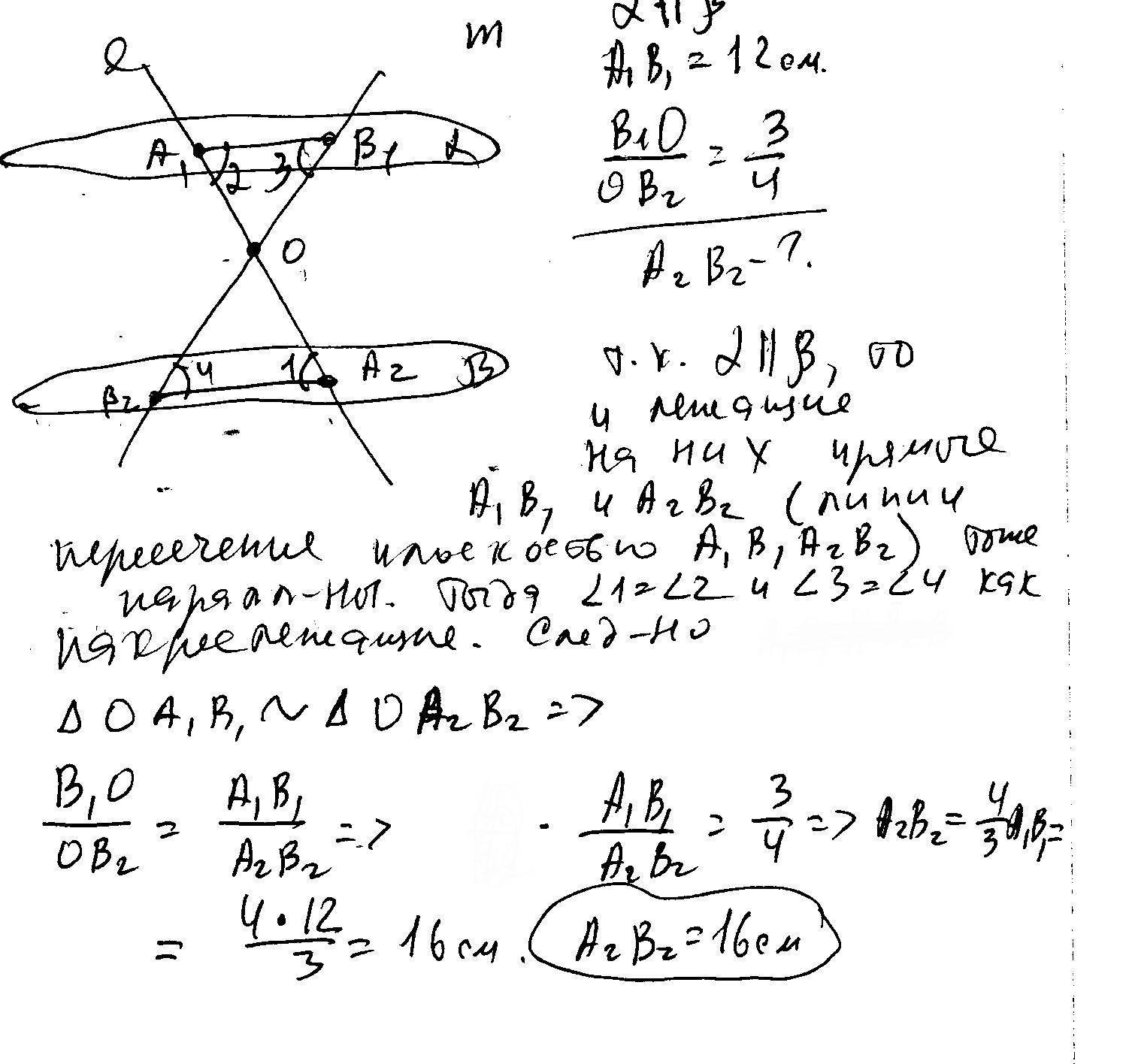
2. Через точку О, лежащую между параллельными плоскостями α и β, проведены прямые l и m.

Прямая l пересекает плоскости α и β в точках А1 и А2 соответственно, прямая m – в точках В1 и В2.

Найдите длину отрезка А2В2, если А1В1 = 12 см, В1О : ОВ2 = 3 : 4.

1. Прямые a и b лежат в параллельных плоскостях α и β.

Могут ли эти прямые

быть : а) параллельными ; б) скрещивающимися?

Сделайте рисунок для

каждого возможного случая.

2. Через точку О, лежащую между параллельными плоскостями α и β,

проведены прямые l и m.

Прямая l пересекает плоскости α и β в точках А1 и

А2 соответственно, прямая m – в точках В1 и В2.

Найдите длину отрезка

А2В2, если А1В1 = 12 см, В1О : ОВ2 = 3 : 4.

Видео:Параллельность прямых. 10 класс.Скачать

1) Всегда ли две не пересекающиеся1) Всегда ли две не пересекающиеся прямые в пространстве параллельны?

1) Всегда ли две не пересекающиеся1) Всегда ли две не пересекающиеся прямые в пространстве параллельны?

2) прямая a скрещивается с прямой b , а прямая b скрещивается с прямой c.

Следует ли отсюда , что прямые a и c скрещиваются?

3)укажите случаи взаимного расположения прямой и плоскости?

4)Даны параллельные прямая и плоскость.

Сколько можно провести в этой плоскости прямых, параллельных данной прямой?

5)прямые a и b параллельны.

Какое положение может занимать прямая aотносительно плоскости, проходящей через прямую b?

6)даны две параллельные прямые.

Через каждую из них проведена плоскость .

Эти две плоскости пересекаются .

Как расположена их линия пересечения относительно данных прямых?

7) через каждую из двух параллельных прямых проведена плоскость .

Можно ли утверждать, что эти плоскости параллельны?

8)могут ли быть параллельными две плоскости , проходящие через не параллельные прямые ?

9)Плоскость α пересекает плоскости β и γ по параллельным прямым.

Будут ли плоскости β и γ параллельны?

10)даны две параллельные плоскости α и β.

Через прямую a плоскости α и точку Aплоскости β проведите мысленно плоскость γ.

Какова взаимное расположение прямой a и линии пересечения плоскостей γ и β?

11)В каком случае параллельной проекций прямой будет точка?

Видео:№16. Параллельные прямые a и b лежат в плоскости α. Докажите,Скачать

Прямые a и b лежат в пересекающихся плоскостях α и β?

Прямые a и b лежат в пересекающихся плоскостях α и β.

Могут ли эти прямые быть : а) параллельными ; б) скрещивающимися?

Сделайте рисунок для каждого возможного случая.

Видео:Параллельные прямые | Математика | TutorOnlineСкачать

Прямые а и в пересекающихся плоскостях альфа и бетта?

Прямые а и в пересекающихся плоскостях альфа и бетта.

Могут ли эти прямые быть — параллельными — скрещивающимися сделать рисунок.

Видео:Параллельность прямой и плоскости. 10 класс.Скачать

1. Прямые а и в лежат в параллельных плоскостях альфа и бетта?

1. Прямые а и в лежат в параллельных плоскостях альфа и бетта.

Могут ли эти прямые быть : а)параллельными.

Сделайте рисунок для каждого возможного случая.

2. Через точку О, лежащую между параллельными плоскостями альфа и бетта, проведены прямые l и m.

Прямая l пересекает плоскости альфа и бетта в точках А1 и А2 соответсвенно прямая m — в точках В1 и В2.

Найдите длину отрезка А2В2, А1В1 = 12см, В1О : ОВ2 = 3 : 4.

3. Изобразите параллелепипед АВСДА1В1С1Д1 и постройте его сечение плоскостью , проходящей через точки М, N и К, являющиеся серединами ребер АВ, ВС и ДД1.

Видео:Геометрия 10 класс (Урок№4 - Параллельность прямых, прямой и плоскости.)Скачать

Прямые a и b лежат в параллельных плоскостях α и β?

Прямые a и b лежат в параллельных плоскостях α и β.

Могут ли эти прямые быть : а) параллельными ; б) скрещивающимися?

Сделайте рисунок для каждого возможного случая.

Видео:Геометрия 10 класс Параллельность прямых, прямой и плоскости теорияСкачать

Прямые a и b лежат в пересекающихся плоскостях α и β?

Прямые a и b лежат в пересекающихся плоскостях α и β.

Могут ли эти прямые быть : а) параллельными ; б) скрещивающимися?

Сделайте рисунок для каждого возможного случая.

Видео:Признаки параллельности прямых. Геометрия 7 класс.Скачать

Прямые a и b лежат в пересекающихся плоскостях α и β?

Прямые a и b лежат в пересекающихся плоскостях α и β.

Могут ли эти прямые быть : а) параллельными ; б) скрещивающимися?

Сделайте рисунок для каждого возможного случая.

Видео:Геометрия 7 класс (Урок№19 - Признаки параллельности прямых.)Скачать

1. Прямые a и b лежат в пересекающихся плоскостях ?

1. Прямые a и b лежат в пересекающихся плоскостях ?

И . Могут ли эти прямые быть : а) параллельными ; б) скрещивающимися?

Сделайте рисунок для каждого возможного случая.

Видео:7 класс, 24 урок, Определение параллельных прямыхСкачать

Прямые a и b лежать в параллельных плоскостях альфа и бета?

Прямые a и b лежать в параллельных плоскостях альфа и бета.

Могут ли эти прямые быть параллельными ; скрещивающимися?

Сделайте рисунок для каждого возможного случая.

Видео:10 класс, 5 урок, Параллельность трех прямыхСкачать

Прямые a и b лежат в параллельных плоскостях?

Прямые a и b лежат в параллельных плоскостях.

Могут ли эти прямые быть : а)параллельными ; б)скрещивающимися?

Вы зашли на страницу вопроса 1. Прямые a и b лежат в параллельных плоскостях α и β?, который относится к категории Геометрия. По уровню сложности вопрос соответствует учебной программе для учащихся 10 — 11 классов. В этой же категории вы найдете ответ и на другие, похожие вопросы по теме, найти который можно с помощью автоматической системы «умный поиск». Интересную информацию можно найти в комментариях-ответах пользователей, с которыми есть обратная связь для обсуждения темы. Если предложенные варианты ответов не удовлетворяют, создайте свой вариант запроса в верхней строке.

Обозначим точку около 60° через Н. Тогда НК — катет, лежащий против угла 30° (в прямоугольном треугольнике сумма острых углов равна 90°). РН = 2 * 5 = 10см (по свойству катета против угла 30° он равен половине гипотенузы) По Пифагору РК = √(РН² — Н..

Кратко : СН = 1 / 2 nk . По теореме о соотношениях сторон и углов треугольника Следовательно : СН = 34 : 2 = 17 см.

1) 3 2) 3 3) 2 4) 1 5) A Б В 3 1 2 6) 2 7) 3.

См. фото. Объем цилиндра равен V = πR²h = 100π, по условию R = 5 см, 25πh = 100π, отсюда h = 100π / 25π = 4 см, АВ = 4см. АD = 2R = 2·5 = 10 см. Найдем площадь осевого сечения цилиндра S(АВСD) = АD·АВ = 10·4 = 40 см². Ответ 40 см².

АВМ — прямоугольный треугольник, следовательно работает теорема Пифагора : AB ^ 2 = x ^ 2 + BM ^ 2 4x ^ 2 = x ^ 2 + 507 3x ^ 2 = 507 x ^ 2 = 507 / 3 = 169 x ^ 2 = 13 x ^ 2 = — 13 (не удовлетворяет условию задачи) АМ = 13 АВ = 13 * 2 = 26.

Так как один угол в тругольнике 90 град. , другой 60 = > третий угол будет 30 В прямоугольном треугольнике, если один угол 30 градусов, то катет равен половине гипотенузы. Гипотенуза + катет = 26, 4 см Катет — х, гипотенуза 2х (так как она в два ра..

48 / 3 = 16(т. К. 3 равные прямые), 16 * 2 = 32.

Площадь равнобедренного треугольника со сторонами a b(a — боковая сторона, b — основание), находится по формуле : S = b / 4 * sqrt(4 * a ^ 2 — b ^ 2) a = 39 b = 30 S = 30 / 4 * sqrt(4 * 39 * 39 — 30 * 30) = 7, 5 * sqrt(6084 — 900) = 7, 5 * 72 = 540 О..

С = 136 — 90 = 46 В = 90 — 46 = 44 (Вроде так я делала, у меня засчитало).

1)апофема равна √((√15)² + 1²) = √16 = 4 Sбок = 4 * (3 + 5) / 2 * 4 = 4 * 4 * 4 = 64 S пол = 64 + 3 * 3 + 5 * 5 = 64 + 9 + 25 = 98 2).

Видео:Параллельность прямой к плоскостиСкачать

Проекции параллельных прямых

Если прямые в пространстве параллельны, то их проекции также параллельны (рис. 5). Доказательство: прямые АВ и CD проецируются с помощью проецирующих плоскостей У и Т, но У¦Т, т. к. АВ¦CD по условию и ААN¦ССN — по построению. Известно, что если две параллельные плоскости пересекаются третьей, то образуются параллельные прямые. Здесь две параллельные плоскости У и Т пересекаются плоскостью проекций ПN и образуются параллельные прямые (АNВN¦CNDN).

Проекции геометрических фигур, параллельных плоскости проекций. Если данная геометрическая фигура — прямая, кривая линия или плоская фигура (треугольник, многоугольник, эллипс, окружность и т. п.) лежит в плоскости, параллельной плоскости проекций, то она проецируется на плоскость проекций в натуральную величину. Доказательство: дано У¦ПN и АВ У (рис. 6). Требуется доказать, что АВ¦АNВN и АВ=АNВN. Так как У¦ПN , то отрезки ААN и ВВN равны и параллельны. Следовательно, четырехугольник АВВNАN является параллелограммом и АВ¦АNВN, АВ=АNВN.

Так же доказывается теорема относительно любой плоской кривой и любой плоской фигуры.

— цилиндрические поверхности в параллельной системе проецирования и конические поверхности в центральной системе проецирования — проецируют пространственные кривые линии и пространственные фигуры.

Основное свойство проецирующей геометрической фигуры заключается в том, что точки, прямые или кривые линии, плоские и пространственные фигуры, расположенные на проецирующей геометрической фигуре, проецируются на линию пересечения этой фигуры с плоскостью проекций. Эта линия называется следом данной проецирующей геометрической фигуры или ее главной проекцией.

На рис. 7 показаны проецирующие геометрические фигуры в ортогональной системе проецирования: проецирующая прямая а, проецирующая плоскость У и проецирующая цилиндрическая поверхность Ф.

Прямая а, плоскость У и образующие цилиндрической поверхности Ф перпендикулярны плоскости проекций ПN . Их главные проекции аN , УN и ФN включают в себя проекции всех точек данной проецирующей геометрической фигуры.

Дополнения однокартинного чертежа. Ранее было показано, что одна проекция точки не определяет ее положения в пространстве.

Для того, чтобы чертеж был полным и обратимым, т.е. для того, чтобы по чертежу можно было представить положение точки в пространстве, применяются разные способы.

Способ числовых отметок. Около проекции точки ставится число, выражающее в некоторых линейных единицах расстояние данной точки от плоскости проекций.

На рис. 8 даны проекции различных геометрических фигур с числовыми отметками.

Около проекции точки А стоит цифра 20. Это означает, что точка А отстоит от плоскости проекций на расстоянии 20 линейных единиц.

Концы отрезка ВС отстоят от плоскости на расстояниях 15 и 30, вершины треугольника DEF — на расстояниях соответственно 0, 10 и 25.

Кривая поверхность задана кривыми линиями, принадлежащими поверхности и параллельными плоскости проекций (горизонталями, если плоскость ПN горизонтальна). Около каждой горизонтали стоит число, выражающее ее расстояние от плоскости ПN.

С помощью горизонталей изображается рельеф земной поверхности на топографических картах и сложные кривые поверхности, в том числе поверхности манекена и обувной колодки.

Проекции, полученные при центральном и параллельном проецировании, обладают рядом свойств.

Проекция точки есть точка. При заданном центре Р (.или направлении S) проецированию любой точки А пространства соответствует иа плоскости проекций п’ единственная точка А’. При этом проекция точки В, лежащей в плоскости проекций, совпадает с самой точкой (см. рис. 43).

Проекция прямой есть прямая. На рис. 46 лучи, проецирующие прямую т, создают плоскость S, которая пересекает плоскость проекций п’ по линии m’, являющейся проекцией на плоскость n’; S

т; S п п = т’. Проекция прямой определена, если известны проекции хотя бы двух ее точек (рис. 9). Если в пространстве прямая параллельна плоскости проекции п’, то ее проекция параллельна самой прямой (рис. 10). При этом при центральном проецировании проекции отрезков пропорциональны самим отрезкам, а при параллельном — равны им.

При параллельном проецировании сохраняется отношение величин отрезков прямой и их проекций (рис. 11):

При параллельном проецировании проекции параллельных прямых есть прямые параллельные (рис. 12). Если прямые т и п в пространстве параллельны, то и проецирующие их плоскости Sm и Sn тоже будут параллельны. При пересечении их с плоскостью проекций п’ получаем т’|| п’.

Проекцией плоскости является плоскость проекций. Плоскость состоит из бесконечного множества точек. При проецировании этого множества проецирующие лучи заполняют все пространство, а их точки пересечения с плоскостью проекций п’ — всю плоскость проекций.

Так как положение любой плоскости в пространстве определяется тремя ее точками, не лежащими на одной прямой, то проекция трех таких точек плоскости (рис. 13, а) устанавливает однозначное соответствие между проецирующей плоскостью и плоскостью проекций n’, которое позволяет определить проекции (рис. 13, б) любой точки D или прямой этой плоскости.

Если плоскость параллельна плоскости проекций, то проекции ее плоских фигур при центральном проецировании подобны самим фигурам (рис. 14, а), а при параллельном — равны им (рис. 14,6).

Если плоскость угла параллельна плоскости проекций, величина проекции угла и при центральном, и при параллельном проецировании равна натуральной величине. На рис. 54, a угол ABC = уголA’B’C’, так как АВС бесконечность А’В’С’, а на рис. 54, б угол ABC = углу А’В’С’, так как АВС = А’В’С’.

При параллельном проецировании проекции фигуры не изменяется при параллельном переносе плоскости j проекций (рис. 15).

Прямые и плоскости (поверхности) могут занимать в пространстве проецирующее положение, если с ними совпадают проецирующие лучи. При центральном проецировании это прямые и плоскости, проходящие через центр проекций, пирамидальные и конические поверхности, у которых вершины совпадают с центром проецирования (рис. 56). При параллельном проецировании — это прямые и плоскости, параллельные направлению проецирования, призматические и цилиндрические поверхности, ребра и образующие которых параллельны направлению проецирования (рис. 57).

Все эти геометрические фигуры можно рассматривать состоящими из проецирующих лучей, каждый из которых изображается точкой. Отсюда следует, что проекциями прямых, плоскостей, поверхностей, занимающих проецирующее положение, есть точки или линии их пересечения с плоскостью проекций («вырожденные» проекции).

Видео:Лекция 1. Классификация прямых линий.Скачать

Взаимное положение двух прямых

Видео:Стереометрия 10 класс. Часть 1 | МатематикаСкачать

Параллельные прямые

К числу свойств параллельного проецирования относится следующее: проекции двух параллельных прямых параллельны между собой. Если (рисунок 2.28) прямая АВ параллельна прямой CD, то проецирующие плоскости; а и /3 параллельны между собой и при пересечении этих плоскостей с плоскостью проекций л₀ получаются параллельные между собой проекции А 0 В 0 и C°D°.

Из указанного свойства параллельного проецирования следует, что горизонтальные проекции параллельных прямых параллельны между собой, фронтальные проекции параллельны между собой и профильные проекции параллельны между собой.

В случае, изображенном на рисунке 2.29 справа, параллельные прямые расположены в общей для них проецирующей плоскости, перпендикулярной к плоскости л,. Поэтому горизонтальные проекции этих прямых расположены на одной прямой.

Видео:Параллельность прямых. Практическая часть. 10 класс.Скачать

Пересекающиеся прямые

Если прямые линии пересекаются, то их одноименные проекции пересекаются между собой в точке, которая является проекцией точки пересечения этих прямых.

Действительно (рисунок 2.30), если точка К принадлежит обеим прямым АВ и CD, то проекция этой точки должна быть точкой пересечения проекций данных прямых.

Заключение о том, что данные на чертеже прямые пересекаются между собой, можно сделать всегда по отношению к прямым общего положения, независимо от того, даны ли проекции на трех или двух плоскостях проекций. Необходимым и достаточным условием является лишь то, чтобы точки пересечения одноименных проекций находились на одном и том же перпендикуляре к соответствующей оси проекций (рисунок 2.31).

🔍 Видео

10 класс, 6 урок, Параллельность прямой и плоскостиСкачать

Лекция 3. Прямая линияСкачать

Параллельные и скрещивающиеся прямые. СтереометрияСкачать

Параллельность прямых и плоскостей в пространстве. Практическая часть - решение задачи. 10 класс.Скачать

Взаимное расположение прямых в пространстве. 10 класс.Скачать

Параллельная проекцияСкачать