Множество четырехугольников множество прямоугольников

Математика | 10 — 11 классы

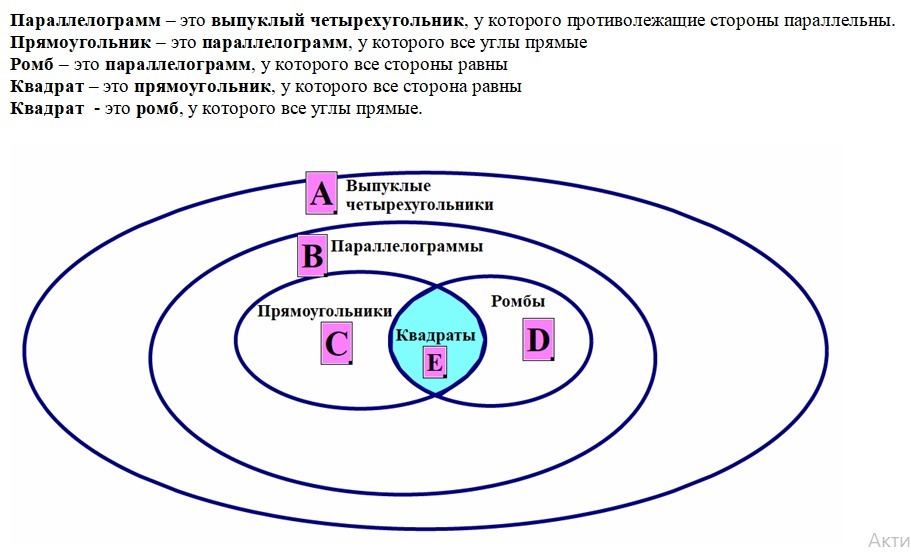
(Задание 5) Отношения между множествами всех выпуклых четырехугольников (А), параллелограммов (В), прямоугольников (С), ромбов (Д) и квадратов (Е) изображены на рисунке 6.

Покажите каждое из множеств.

Параллелограмм – это выпуклый четырехугольник, у которого противолежащие стороны параллельны.

Прямоугольник – это параллелограмм, у которого все углы прямые

Ромб – это параллелограмм, у которого все стороны равны

Квадрат – это прямоугольник, у которого все сторона равны

Квадрат — это ромб, у которого все углы прямые.

Видео:Как изображать множества на диаграммахСкачать

В — МНОЖЕСТВО ТРЕУГОЛЬНИКОВ С — МНОЖЕСТВО ЧЕТЫРЕХУГОЛЬНИКОВ Д — МНОЖЕСТВО ПРЯМОУГОЛЬНИКОВ Е — МНОЖЕСТВО КВАДРАТОВ А — МНОЖЕСТВО МНОГОУГОЛЬНИКОВ?

В — МНОЖЕСТВО ТРЕУГОЛЬНИКОВ С — МНОЖЕСТВО ЧЕТЫРЕХУГОЛЬНИКОВ Д — МНОЖЕСТВО ПРЯМОУГОЛЬНИКОВ Е — МНОЖЕСТВО КВАДРАТОВ А — МНОЖЕСТВО МНОГОУГОЛЬНИКОВ.

Какие из этих множеств являются подмножествами других множеств?

Видео:Множества. Операции над множествами. 10 класс алгебраСкачать

ПОМОГИТЕ РЕШИТЬ ПОЖАЛУЙСТА ЗАВТРА СДАВАТЬ?

ПОМОГИТЕ РЕШИТЬ ПОЖАЛУЙСТА ЗАВТРА СДАВАТЬ!

Даны множества А, В, С.

Изобразите отношения между ними.

Укажите характеристическое свойство множеств АUВ, А∩С, А В, А ∩ (В С) : № 11.

А – множество учащихся в школе ;

В – множество девочек в школе ;

С – множество учащихся третьих классов в этой школе.

А – множество натуральных чисел ;

В – множество натуральных чисел, кратных 5 ;

С – множество натуральных чисел, кратных 4.

А – множество параллелограммов ;

В – множество четырехугольников ;

С – множество прямоугольников.

А – множество прямоугольников ;

В – множество четырехугольников ;

С – множество квадратов.

А – множество треугольников ;

В – множество прямоугольных треугольников ;

С – множество равнобедренных треугольников.

А – множество трапеций ;

В – множество параллелограммов ;

С – множество четырехугольников, имеющих прямой угол.

А – множество прямоугольных треугольников ;

В – множество равносторонних треугольников ;

С – множество равнобедренных треугольников.

А – множество натуральных чисел, кратных 5 ;

В – множество натуральных чисел, кратных 3 ;

С – множество натуральных чисел, кратных 4.

А – множество натуральных чисел, кратных 2 ;

В – множество натуральных чисел, кратных 3 ;

С – множество натуральных чисел, кратных 5.

А – множество параллелограммов ;

В – множество квадратов ;

С – множество ромбов.

Видео:Множество. Элементы множества. 5 класс.Скачать

Как может называться множество квадрат ромб круг?

Как может называться множество квадрат ромб круг?

Видео:Параллелограмм, прямоугольник, ромб,квадрат,трапеция, все свойства и определения!!!Скачать

Найдите на рисунке все параллелограммы, ромбы, прямоугольники, квадраты?

Найдите на рисунке все параллелограммы, ромбы, прямоугольники, квадраты!

Видео:Математика 2 класс (Урок№36 - Прямоугольник.)Скачать

Решите систему неравенств?

Решите систему неравенств.

На каком из рисунков изображено множество ее решений?

Видео:Свойства диагоналей прямоугольника. Геометрия 8 класс. Тесты. Четырехугольники. Математика.Скачать

Какой четырехугольник не имеет оси симметрии?

Какой четырехугольник не имеет оси симметрии?

A) ромб б) прямоугольник в) параллелограмм г) квадрат.

Видео:Как решить любую задачу с четырёхугольниками? | Математика TutorOnlineСкачать

Какие из данных четырехугольников не являются параллелограммами 1 квадрат 2 прямоугольник 3 ромб 4 трапеция?

Какие из данных четырехугольников не являются параллелограммами 1 квадрат 2 прямоугольник 3 ромб 4 трапеция.

Видео:Миникурс по геометрии. ЧетырехугольникиСкачать

Построй диаграмму Венна для множества А, В, С, Д, где А — множество всех четырехугольников, В — множество ромбов, С — множество квадратов, д — множество прямоугольников?

Построй диаграмму Венна для множества А, В, С, Д, где А — множество всех четырехугольников, В — множество ромбов, С — множество квадратов, д — множество прямоугольников.

Видео:Урок Множество 1 классСкачать

Запиши множество острых , множество прямых и множество тупых углов на рисунке ?

Запиши множество острых , множество прямых и множество тупых углов на рисунке .

Есть ли среди данных фигур прямоугольники .

Из букв входящих в каждой множество составь слова.

Видео:Математика 29. Четырехугольники, прямоугольник, квадрат — Шишкина школаСкачать

Запиши множества острых, множество прямых и множество тупых углов на рисунке?

Запиши множества острых, множество прямых и множество тупых углов на рисунке.

Есть ли среди данных фигур прямоугольники?

На этой странице находится ответ на вопрос (Задание 5) Отношения между множествами всех выпуклых четырехугольников (А), параллелограммов (В), прямоугольников (С), ромбов (Д) и квадратов (Е) изображены на рисунке 6?, из категории Математика, соответствующий программе для 10 — 11 классов. Чтобы посмотреть другие ответы воспользуйтесь «умным поиском»: с помощью ключевых слов подберите похожие вопросы и ответы в категории Математика. Ответ, полностью соответствующий критериям вашего поиска, можно найти с помощью простого интерфейса: нажмите кнопку вверху страницы и сформулируйте вопрос иначе. Обратите внимание на варианты ответов других пользователей, которые можно не только просмотреть, но и прокомментировать.

2х — 4у + 5 = 0 2х = 4у — 5 х = 2у — 5 / 2 х = 2у — 5 / 2, у€R.

1) 1800 / 3 = 600 км / ч — скорость самолета 2) 400 / 8 = 50 км / ч — скорость поезда 3) 600 / 50 = 12 раз — самолет двигается быстрее поезда Ответ : в 12 раз.

1)1800 : 3 = 600(км / ч) — самолет 2)400 : 8 = 50(км / ч) — поезд 3)600 : 50 = в 12 раз быстрее самолет чем поезд.

1) 20350 / 55 = 370 (см) — сторона b 2) 2 * (55 + 370) = 850 (см2) — площадь ящика.

221 + X = 407 X = 407 — 221 X = 186 Проверка : 221 + 186 = 407 Ответ : 186.

Да, такое может быть. Пример : х = 10, у = 2.

Вот готово. Надеюсь это тема тебе понятна потому что она самая легкая.

1. 4 : 7 = 0. 2см 0. 2×2 = 0. 4см или 4 мм.

1)1. 4 : 7 * 2 = 4см Незнаю точно помоему так.

1)Высота кружки (10 см). Так как 10 мм (1 см) это слишком маленькая, а 10 дм (100 см) слишком большая. 2)Высота комнаты (30 км (3. 000 см) ). Так как 30 см слишком маленькая и 30 дм (300 см) тоже. 3)Рост ученика (100 см). Так как 100 мм (10 см)..

Видео:ПОДМНОЖЕСТВА. Операции над множества. §14 алгебра 8 классСкачать

Теория множеств (стр. 1 )

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3

«Высшее назначение математики состоит в том, чтобы находить скрытый порядок в хаосе, который нас окружает»

Подсознательно первые представления о множестве у человека начинают формироваться с момента рождения, когда он погружается в удивительно многообразный мир окружающих его объектов и явлений. В нем уже генетически заложены возможности ускоренно воспроизвести весь опыт общения с этим миром, накопленный человечеством за многовековую историю. С первых же шагов мы не просто пополняем список знакомых нам объектов и явлений, а начинаем дифференцировать и классифицировать их по определенным свойствам (горячие и холодные, сладкие и горькие, тяжелые и легкие, красные и зеленые и т. д.), объединяя тем самым объекты в некоторые совокупности. Первый же опыт общения с ними убеждает нас и в том, что каждый объект имеет сложную структуру (кто из нас не ломал ни одной игрушки, пытаясь уяснить из чего она состоит), представляет собой как бы определенную совокупность других объектов, из которых как из составляющих состоит сам.

Теория множеств – создана в конце XIX века великим немецким математиком Георгом Кантором (1845 – 1918). Благодаря этой теории были получены ответы на вопросы, не дававшие покоя математикам на протяжении нескольких веков.

Главная заслуга Кантора состоит в признании того факта, что бесконечность – это не абстракция, придуманная философами, а реальность; что бесконечные совокупности предметов существуют наравне с конечными.

Кантор показал, что бесконечными множествами можно оперировать точно так же, как и конечными, он научился определять «размеры» бесконечных множеств, сравнивать их между собой. Одним словом, благодаря его открытиям бесконечные множества стали рабочим аппаратом математики.

В ходе изучения темы « Теория множеств» студент должен:

1. знать основные понятия теории множеств, такие как: множество, элементы множества, подмножество, пустое множество, множества бесконечные, множества конечные, равные множества, объединение множеств, пересечение множеств, разность множеств, симметрическая разность множеств, универсальное множество, упорядоченное множество; знать способы задания множеств, свойства операций над множествами.

2. уметь изображать алгебраические операции над множествами (отношения между множествами) с помощью диаграмм (кругов) Эйлера-Венна; доказывать и объяснять некоторые свойства операций над множествами, выполнять алгебраические операции над множествами; решать задачи типа:

Даны множества: A= ; D= , B= F= , C= , V= . Укажите, какие из данных множеств являются подмножествами множества А. Верно ли, что множество F является подмножеством множества D, а множество V – подмножеством множества C?

2. Какие из следующих множеств геометрических фигур на плоскости равны между собой, если:
А – множество всех квадратов;
В – множество всех прямоугольников;
С – множество всех четырехугольников с прямыми углами;
Д – множество всех прямоугольников с равными сторонами;
F – множество всех ромбов с прямыми углами.

3. Для каждого из слов: «корректор», «аргон», «гонорар», «ректор», «редактор», «декоратор» составьте множество его различных букв. Имеются ли среди них равные?

4. Даны множества: U – множество студентов ЧелГУ, A – подмножество студентов исторического факультета, B – подмножество студентов филологического факультета, C – подмножество студентов факультета журналистики, D – спортсменов университета. Изобразите эти множества с помощью диаграмм Эйлера-Венна.

Даны два множества А = и В = . Найти объединение, пересечение, разности этих множеств.

Примерный вариант решения задач.

Даны множества: A= ; D= , B= F= , C= , V= . Укажите, какие из данных множеств являются подмножествами множества А. Верно ли, что множество F является подмножеством множества D, а множество V – подмножеством множества C?

Решение: т. к. каждый элемент множества D принадлежит множеству A, то D Ì A. Рассуждая аналогично, получаем, что B Ì A; F Ì A; V Ì A. Множество C не является подмножеством множества A, т. к. содержит элемент 0, который не принадлежит данному множеству A.

Т. к. каждый элемент множества F принадлежит множеству D, то F Ì D. Аналогичные рассуждения приводят к выводу, что F Ì C.

Ответ: D Ì A; B Ì A; F Ì A; V Ì A. F Ì D; F Ì C.

2. Какие из следующих множеств геометрических фигур на плоскости равны между собой, если:
А – множество всех квадратов;
В – множество всех прямоугольников;
С – множество всех четырехугольников с прямыми углами;
Д – множество всех прямоугольников с равными сторонами; F – множество всех ромбов с прямыми углами.

Решение: вспомнив определение и свойства геометрических фигур на плоскости, можно сделать заключение, что А = Д = F; В = С.

Ответ: А = Д = F; В = С.

3. Для каждого из слов: «корректор», «аргон», «гонорар», «ректор», «редактор», «декоратор» составьте множество его различных букв. Имеются ли среди них равные?

Решение: Для определенности введем обозначения множеств:
множество различных букв для слова «корректор» обозначим A, получим А = ,
множество различных букв для слова «аргон» обозначим B, получим В = ,
множество различных букв для слова «гонорар» обозначим C, получим С = ,
множество различных букв для слова «ректор» обозначим D, получим Д = ,
множество различных букв для слова «редактор» обозначим E, получим E = ,
множество различных букв для слова «декоратор» обозначим F, получим F = .

Т. к. каждый элемент множества A принадлежит множеству D, и каждый элемент множества D принадлежит множеству А, то А = D. Аналогичные рассуждения приводят к выводу, что В = C, E=F.

4. Даны множества: U – множество студентов ЧелГУ, A – подмножество студентов исторического факультета, B – подмножество студентов филологического факультета, C – подмножество студентов факультета журналистики, D – спортсменов университета. Изобразите эти множества с помощью диаграмм Эйлера-Венна.

Решение: Множества A, B, C, D являются подмножествами одного множества U. Значит, U – универсальное множество, на диаграмме Эйлера-Венна изобразим его с помощью прямоугольника. Множества A, B, C – непересекающиеся, но спортсменами университета могут быть как студенты исторического, филологического факультетов, факультета журналистики, так и студенты других факультетов университета.

Ответ:

Даны два множества А = и В = . Найти объединение, пересечение, разности этих множеств.

Решение: Используем определение алгебраических операций над множествами:

Объединением (суммой) множеств А и В называется множество, состоящее из всех элементов, принадлежащих хотя бы одному из множеств А или В, следовательно, A È B = .
Пересечением (произведением) множеств А и В называется множество, состоящее из всех элементов, принадлежащих обоим множествам А и В, следовательно, А Ç В = .
Разностью множеств А и В называется множество элементов, принадлежащих множеству А, которые не принадлежат множеству В, следовательно, А В = ; В А = .
Симметрической разностью (дизъюнктивной суммой) множеств А и В называется множество элементов, принадлежащих или множеству А, или множеству В (но не обоим вместе), следовательно, А ∆ В = .

Глоссарий по теме «Множества»

Множество – первичное понятие математики. Это совокупность каких-либо объектов.

Множества бесконечные – множества, состоящие из бесконечного числа элементов

Множества конечные – множества, состоящие из конечного числа элементов (причем неважно, известно это число или нет, главное, оно существует)

Объединение множеств – объединением (суммой) множеств А и В называется множество, состоящее из всех элементов, принадлежащих хотя бы одному из множеств А или В.

Пересечение множеств – пересечением (произведением) множеств А и В называется множество, состоящее из всех элементов, принадлежащих обоим множествам А и В.

Подмножество – множество B называют подмножеством множества А, если каждый элемент множества В принадлежит А.

Пустое множество – множество, которое не содержит ни одного элемента

Равные множества – множества А и В называют равными (А = В), если каждое из них является подмножеством другого.

Разность множеств – разностью множеств А и В называется множество элементов, принадлежащих множеству А, которые не принадлежат множеству В.

Симметрическая разность множеств – симметрической разностью (дизъюнктивной суммой) множеств А и В называется множество элементов, принадлежащих или множеству А, или множеству В (но не обоим вместе).

Универсальное множество – совокупность допустимых объектов

Упорядоченное множество – множество с установленным порядком расположения элементов

Элементы множества – объекты, входящие в данное множество.

УПРАЖНЕНИЯ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ

Приведите примеры различных множеств. Приведите пример равных множеств. Сколько можно образовать подмножеств из множества Х = . Заданы два множества А и В (см. таблицу). Определить множества АÈВ, АÇВ, АВ, ВА, А∆В.

По данным промежуткам А и В (см. таблицу) на числовой прямой, определить множества АÈВ, АÇВ, АВ, ВА, А∆В.

ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ ПО ТЕМЕ «ТЕОРИЯ МНОЖЕСТВ»

1. Объясните понятие «множество».

2. Объясните понятие «элемент множества».

3. Как обозначаются множества, его элементы?

4. Как читается и что обозначает запись «х Î Х»?

5. Дайте определение конечного и бесконечного множества.

6. Какое множество обозначается с помощью символа «Æ»?

7. Дайте определение подмножества.

8. Какие множества называются равными?

9. Объясните понятие «универсальное множество».

10. Что называется объединением множеств?

11. Что называется пересечением множеств?

12. Что называется разностью множеств?

13. Что называется симметрической разностью множеств?

14. Как изображаются алгебраические операции над множествами?

15. Мощность множеств.

16. Выполните решение задач

1. Приведите примеры различных множеств.

2. Приведите пример равных множеств.

3. Для каждого из слов «заголовок» и «репортер» составьте множество его различных букв. Равны ли эти множества? Приведите пример слова, множество различных букв которого будет подмножеством множества различных букв, образованного из слова «заголовок».

4. Образуйте всевозможные подмножества из множества Y=.

5. Заданы два множества А= и В=. Найти пересечение, объединение и разности этих множеств.

6. По числовым промежуткам А= (–2; 3] и В= [0; ¥) на числовой прямой определить множества A È B, А Ç В, АВ, ВА.

1. , Шикина : Пути знакомства. Основные понятия. Методы. Модели. (Гуманитариям о математике): Учебник. М.: Эдиториал УРСС, 2001. – 272 с.

2. Грес для гуманитариев: Уч. пособие / . – М.: Юрайт, 2000. – 112 с.

3. , Савин о математике. Книга 1. Дискретные объекты. – М.: ФИМА, МЦНМО, 2002. – 368 с.

4. Курс математики (для гуманитарных специальностей вузов): Учебно-методическое пособие / ЧГАКИ. – челябинск, 200. – 45 с.

5. , , : Учебное пособие. Математика. Лекции, задачи, решения. – Альфа.

ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ ЛОГИКИ.

«Математику уже затем учить надо, что она ум в порядок приводит».

Логика (от древнегреческого logos – слово, выражающее мысль) является началом любой научной теории. Логика как наука о способах мышления, приводящих к истине, возникла в глубокой древности.

Начало науки о законах и формах мышления связывают с именем Аристотеля. Именно Аристо–322 гг. до н. э.) создал чистую систему силлогизмов – правил вывода, что и привело к возникновению теории логики. Математическое исследование этих вопросов берет свое начало от основополагающего труда Джорджа Буля, изданного в Лондоне в 1854 году. Этот труд Буля положил начало математической логики, систематическое развитие которой было достигнуто работами многих математиков XX века.

Правила вывода позволяют преобразовывать исходные утверждения подобно тому, как тождественные преобразования в математике дают возможность решать различные системы уравнений. Следующим шагом формализации логики является появление специальной символики для точной и компактной записи утверждений и определения операций над ними.

Идея перенесения тех методов, которые обычно применяются в математике, на логику была реализована Б. Паскалем (), Г. Лейбницем (), Дж. Булем (), О. Де Морганом (), Г. Фреге (), Б. Расселом (), Д. Гильбертом (), А. Марковым () и др. Так появился язык логики как логическое продолжение языка математики.

С появлением языка математической логики стало возможным составлять алгоритмы логического вывода. Стали вести речь о создании «искусственного интеллекта». В последнее время логика находит все более широкое применение в технике при исследовании и разработке вычислительных машин, дискретных автоматов. Ее методы используются в теории преобразования и передачи информации, теории вероятностей и комбинаторном анализе. Математическая логика находит свое применение в экономике, биологии, медицине, психологии, праве, языкознании.

Сложившийся стереотип о том, что математическая логика – наука, изучающая законы мышления с применением аппарата математики, главным образом, для нужд самой математики, в современных условиях меняется коренным образом. С расширением области применения и дальнейшим развитием математической логики изменяется и взгляд на нее. Объектами математической логики являются любые дискретные конечные системы, а ее главная задача – структурное моделирование таких систем.

В ходе изучения темы « Элементы математической логики» студент должен:

1. знать основные понятия математической логики, такие как: высказывание, свойства высказывания (закон исключения третьего, закон противоречия), предикат, кванторы общности и существования, алгебра высказываний (операции над высказываниями), основные свойства операций над высказываниями, истинностные таблицы, тавтология.

2. уметь доказывать и объяснять некоторые свойства операций над высказываниями; выполнять алгебраические операции над высказываниями (строить таблицы истинности алгебраических операций над высказываниями); решать задачи типа:

Видео:Геометрия 10 класс (Урок№2 - Четырехугольники.)Скачать

Презентация на тему: «Теория множеств. Множество и его элементы».

Видео:8 класс, 3 урок, ЧетырехугольникСкачать

«Управление общеобразовательной организацией:
новые тенденции и современные технологии»

Свидетельство и скидка на обучение каждому участнику

Описание презентации по отдельным слайдам:

Теория множеств. Множество и его элементы.

Обозначения: ϵ ∉ Ø ᴄ ; ȼ Ǝ ∄ ∩ ∪ ⎺ — какие элементы заключены в то или иное подмножество; — знак принадлежности элемента множеству; — знак отрицания принадлежности элемента множеству; — обозначение пустого множества; — Обозначение вложенности и не вложенности одного множества в другое; обозначение существования какого-либа элемента или множества; обозначение не существования какого-либо элемента или множества; обозначение пересечения множеств; обозначение объединения множеств; обозначение отрицания: «не»; — обозначение дополнения;

Под множеством понимают совокупность объектов любой природы, обладающих некоторым общим свойством. Основатель теории множеств Георг Кантор определил множество как «многое, мыслимое нами, как единое».

Пример. ; . S = – множество, содержащее целые числа. Заметим, что множество S совпадает с одним из множеств, выписанных левее, поскольку порядок, в котором записываются элементы множества, значения не имеет.

Пример Все элементы множества С = содержатся в множестве Z = . Записывается это так: С ϲ Z.

Задача: Определить, какие из перечисленных множеств включаются одни в другие: а) множество всех действительных чисел R; б) множество всех рациональных чисел Q; в) множество всех целых чисел Z; г) множество всех натуральных чисел N. Решение: N ϲ Z ϲ Q ϲ R

Задача: Пусть U есть множество: а) всех целых чисел; б) всех прямоугольников на плоскости; в) всех ромбов на плоскости; Множество А пусть соответственно есть: а) множество всех четных чисел; б) множество всех квадратов; в) множество всех квадратов. Определить какие из перечисленных множеств включены одни в другие? Решение: а) А ϲ U б) A ϲ U в) A ϲ U

Задача: М-множество четырехугольников. Принадлежит ли этому множеству: 1) ромб; 2) трапеция; 3) окружность; 4) прямоугольник; 5) диагональ квадрата; 6)призма? Решение: ϵМ ∉ М

Определение: Пусть дана некоторая совокупность элементов, которую обозначим: А=. Предположим, что часть элементов 1,2,4 и 6 имеют круглую форму, 2,3,4,8 и 9 – окрашены в белый цвет. В этом случае говорят, что множество А имеет два подмножества: В= и С=. Принято говорить, что множество А – фундаментально, а подмножества В и С – просто множества.

В результате мы имеем еще несколько подмножеств: К1 = – белые элементы круглой формы; К2 = — элементы, не обладающие ни одним из рассматриваемых свойств; К3 = — элементы исключительно круглые; К4 = – элементы исключительно белые. А=. 1,2,4 и 6 имеют круглую форму, 2,3,4,8 и 9 – окрашены в белый цвет.

Задача: Дано множество К=. Составить подмножество Р из чисел, которые: 1) делятся на 7; 2) делятся на 9; 3) не делятся на 5. Решение: 1– ϵ Р 2– ϵ Р 3- ϵ Р

Определение: Если все элементы множества А являются элементами множества В, то Пример: А-множество букв слова «Весна», В-множество букв слова «Навес». А=В. А=В

Определения: Множество конечно, если оно содержит конечное число элементов. Множество бесконечно, если оно содержит бесконечное число элементов.

Определение: Множество называется пустым, если оно не содержит элементов. Ø – обозначение пустого множества.

Пример: а)М-множество действительных корней квадратного уравнения х2+1=0; б)К множество всех четных чисел; в) В-множество всех студентов группы СТ; г) С-множество прямоугольных треугольников, у которых сумма квадратов катетов не равна квадрату гипотенузы? д) Т-множество целых корней уравнения х2-9=0. а) Данное множество является пустым, т.к. корней данное уравнение не имеет б) Данное множество бесконечно, т.к. число четных чисел – бесконечно. в) Данное множество является конечным, т.к. число студентов в группе СТ – конечно. г) Данное множество является пустым, т.к. в прямоугольном треугольнике сумма квадратов катетов всегда равна квадрату гипотенузы. д) Данное множество конечно, т.к. уравнение имеет два Целых корня: 3 и -3.

Решение: Параллелограммы – это множество четырехугольников, у которых попарные стороны параллельны и равны между собой. Квадраты – это множество прямоугольников, у которых все стороны равны. Прямоугольники – это множество параллелограммов, у которых все углы равны 90 градусов. Равнобедренные треугольники – это множество треугольников, у которых две стороны равны. Прямоугольные треугольники – это множество треугольников, у которых один угол равен 90 градусов. Задача: Задать характеристическим свойством множество: 1) всех параллелограммов; 2)всех квадратов; 3)всех прямоугольников; 4)всех равнобедренных треугольников; 5)всех прямоугольных треугольников.

В математике часто приходится определять принадлежность данного элемента конкретному множеству. Множество – совокупность объектов, ……………… называемых элементами множества . Рефлексия Вставьте пропущенные слова:

Самостоятельно: Обозначения некоторых числовых множеств: N – множество натуральных чисел; Z – множество целых чисел; Q – множество рациональных чисел; R – множество действительных чисел Запишите на символическом языке следующее утверждение: а) число 10 – натуральное ____________________ б) число – 7 не является натуральным ___________ в) число – 100 является целым _________________ г) число 2,5 – не целое _________________

Самостоятельно: Среди перечисленных ниже множеств укажите конечные и бесконечные множества: а) множество чисел, кратных 13; б) множество делителей числа 15; в) множество деревьев в лесу; г) множество натуральных чисел; д) множество рек Ростовской области; е) множество корней уравнения х + 3 = 11; ж) множество решений неравенства х + 1 23 слайд

Спасибо за урок! Домашнее задание. Стр. 36 Задание 4,5, 6-10.

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 953 человека из 79 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 330 человек из 69 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 679 человек из 74 регионов

Ищем педагогов в команду «Инфоурок»

• Сугак Татьяна ВасильевнаНаписать 1719 16.05.2017

Номер материала: ДБ-479677

16.05.2017 795

16.05.2017 978

16.05.2017 717

16.05.2017 1057

16.05.2017 694

16.05.2017 1582

16.05.2017 662

Не нашли то, что искали?

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

В России стартует пилотный проект по реабилитации детей-инвалидов

Время чтения: 2 минуты

Названы главные риски для детей на зимних каникулах

Время чтения: 3 минуты

Во всех педвузах страны появятся технопарки

Время чтения: 1 минута

Итоговое сочинение успешно написали более 97% выпускников школ

Время чтения: 2 минуты

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

В Минпросвещения рассказали о формате обучения школьников после праздников

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

📸 Видео

Математика. 3 класс. Множества. ПодмножестваСкачать

Четырехугольники. Вебинар | МатематикаСкачать

Площади четырехугольников: трапеция, параллелограмм, ромб. Геометрия на клеточке. ОГЭСкачать

А.5.3 Четырехугольники (+ Д/З)Скачать

9 класс, 2 урок, Множества и операции над нимиСкачать

Математика. Множество и его элементыСкачать

Числовые множества, 6 классСкачать