Метрики расстояния между векторами

Дата публикации Jan 13, 2019

Ряд алгоритмов машинного обучения — контролируемых или неконтролируемых — используют метрики расстояния, чтобы знать шаблон входных данных для принятия любого решения на основе данных. Хороший показатель расстояния помогает значительно повысить производительность процессов классификации, кластеризации и поиска информации. В этой статье мы обсудим различные метрики расстояния и то, как они помогают в моделировании машинного обучения.

Видео:расстояние между прямыми в метрике МинковскогоСкачать

Введение

Во многих реальных приложениях мы используем алгоритмы машинного обучения для классификации или распознавания изображений, а также для извлечения информации из содержимого изображения. Например, распознавание лиц, цензурированные изображения в Интернете, розничный каталог, системы рекомендаций и т. Д. Здесь очень важно выбрать хороший показатель расстояния. Метрика расстояния помогает алгоритмам распознавать сходства между содержимым.

Определение базовой математики (Источник Википедия),

Метрика расстояния использует функцию расстояния, которая обеспечивает метрику отношения между каждым элементом в наборе данных.

Некоторые из вас могут подумать, что это за функция расстояния? как это работает? как он решает, что определенный контент или элемент данных имеет какие-либо отношения с другим? Что ж, давайте попробуем выяснить это в следующих нескольких разделах.

Видео:А.5.9 Евклидово расстояние между точками (длина отрезка)Скачать

Функция расстояния

Вы помните изучение теоремы Пифагора? Если вы это сделаете, то вы можете вспомнить вычисление расстояния между двумя точками данных, используя теорему.

Чтобы вычислить расстояние между точками данных A и B, в теореме Пифагора рассматривается длина осей x и y.

Многим из вас должно быть интересно, используем ли мы эту теорему в алгоритме машинного обучения, чтобы найти расстояние? Чтобы ответить на ваш вопрос, да, мы используем его. Во многих алгоритмах машинного обучения мы используем приведенную выше формулу в качестве функции расстояния. Мы поговорим об алгоритмах, где он используется.

Теперь вы, наверное, поняли, что такое функция расстояния? Вот упрощенное определение.

Основное определение от Math.net,

Функция расстояния обеспечивает расстояние между элементами набора. Если расстояние равно нулю, то элементы эквивалентны, иначе они отличаются друг от друга.

Функция расстояния — это не что иное, как математическая формула, используемая метриками расстояния. Функция расстояния может отличаться в зависимости от метрики расстояния. Давайте поговорим о различных дистанционных метриках и поймем их роль в моделировании машинного обучения.

Видео:Метрики и расстоянияСкачать

Метрики расстояния

Существует несколько метрик расстояния, но для краткости этой статьи мы обсудим лишь несколько широко используемых метрик расстояния. Сначала мы попытаемся понять математику, стоящую за этими метриками, а затем определим алгоритмы машинного обучения, в которых мы используем эти метрики расстояния.

Ниже приведены часто используемые метрики расстояния —

Видео:Видеоурок "Расстояние между прямыми в пространстве"Скачать

Минковский Расстояние:

Расстояние Минковского является метрикой в ​​нормированном векторном пространстве. Что такое нормированное векторное пространство? Нормированное векторное пространство — это векторное пространство, в котором определена норма. Предположим, что X — векторное пространство, тогда норма на X — вещественная функция ||Икс|| который удовлетворяет условиям ниже —

1. Нулевой вектор-Нулевой вектор будет иметь нулевую длину.
2. Скалярный фактор-Направление вектора не меняется, когда вы умножаете его на положительное число, хотя его длина будет изменена.
3. Неравенство треугольникаЕсли расстояние является нормой, то рассчитанное расстояние между двумя точками всегда будет прямой линией.

Вам может быть интересно, зачем нам нужен нормированный вектор, не можем ли мы просто перейти к простым метрикам? Поскольку нормированный вектор обладает указанными выше свойствами, это помогает поддерживать индуцированную норму метрико-однородной и трансляционной инвариантом. Более подробную информацию можно найтиВот,

Расстояние можно рассчитать по приведенной ниже формуле —

Расстояние Минковского является обобщенной метрикой расстояния. Здесь обобщенный означает, что мы можем манипулировать приведенной выше формулой, чтобы рассчитать расстояние между двумя точками данных различными способами.

Как уже упоминалось выше, мы можем манипулировать значениемпи рассчитать расстояние тремя разными способами-

р = 2, евклидово расстояние

р = ∞, расстояние чебычева

Мы обсудим эти метрики расстояния ниже подробно.

Манхэттен Расстояние:

Мы используем Манхэттенское расстояние, если нам нужно рассчитать расстояние между двумя точками данных в виде сетки, как путь. Как уже упоминалось выше, мы используемМинковское расстояниеформула, чтобы найти расстояние Манхэттена, установивр-хзначение как1,

Допустим, мы хотим рассчитать расстояние,dмежду двумя точками данныхИкса такжеY

Расстояниеdбудет рассчитываться с использованиемабсолютная сумма разностеймежду его декартовыми координатами, как показано ниже:

где, n- количество переменных,XIа такжеугявляются переменными векторов x и y соответственно в двумерном векторном пространстве. то естьх = (х1, х2, х3, . )а такжеу = (у1, у2, у3,…),

Теперь расстояниеdбудет рассчитываться как

(x1 — y1)+(x2 — y2)+(х3 — у3)+… +(xn — yn),

Если вы попытаетесь визуализировать расчет расстояния, он будет выглядеть примерно так:

Расстояние до Манхэттена также известно как геометрия такси, расстояние до городских кварталов и т.д.

Евклидово расстояние:

Евклидово расстояние — одна из наиболее часто используемых метрик расстояния. Он рассчитывается по формуле Минковского расстояния путем установкир-хзначение для2, Это обновит расстояние«D»формула как ниже:

Давай остановимся ненадолго! Эта формула выглядит знакомо? Ну да, мы только что видели эту формулу выше в этой статье при обсуждении«Теорема Пифагора».

Евклидова формула расстояния может быть использована для расчета расстояния между двумя точками данных на плоскости.

Видео:Евклидово расстояние на пальцах. Как определить расстояние между двумя точками.Скачать

Расстояние косинуса:

В основном, метрика косинусного расстояния используется для поиска сходства между различными документами. В косинусной метрике мы измеряем степень угла между двумя документами / векторами (термин частоты в разных документах собирается как метрика). Эта конкретная метрика используется, когда величина между векторами не имеет значения, но ориентация.

Формула подобия косинуса может быть получена из уравнения точечных произведений:

Теперь вы должны подумать, какое значение угла косинуса будет полезно для определения сходства.

Теперь, когда у нас есть значения, которые будут рассматриваться для измерения сходства, нам нужно знать, что означают 1, 0 и -1.

Здесь значение косинуса 1 предназначено для векторов, указывающих в одном и том же направлении, то есть между документами / точками данных есть сходства. В нуле для ортогональных векторов, т. Е. Не связанных (найдено некоторое сходство). Значение -1 для векторов, указывающих в противоположных направлениях (без сходства).

Видео:Расстояние между точкамиСкачать

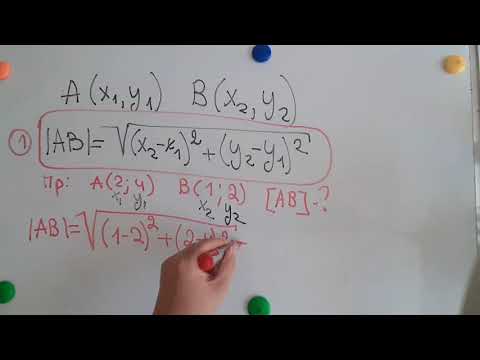
Махаланобис Расстояние:

Расстояние Махаланобиса используется для расчета расстояния между двумя точками данных в многомерном пространстве.

Согласно определению Википедии,

Махаланобис расстояниеявляется мерой расстояния между точкой P и распределением D. Идея измерения состоит в том, сколько стандартных отклонений P от среднего значения D.

Преимущество использования расстояния по махаланобису заключается в том, что учитывается ковариация, которая помогает измерять силу / сходство между двумя различными объектами данных. Расстояние между наблюдением и средним может быть рассчитано, как показано ниже:

Здесь S — ковариационные метрики. Мы используем обратную метрику ковариации, чтобы получить нормализованное по дисперсии уравнение расстояния.

Теперь, когда у нас есть базовое представление о различных метриках расстояния, мы можем перейти к следующему шагу, а именно к методам / моделированию машинного обучения, в которых используются эти метрики различий.

Видео:Определение кратчайшего расстояние между скрещивающимися прямыми методом замены плоскостей проекцииСкачать

Моделирование машинного обучения и дистанционные метрики

В этом разделе мы будем работать над некоторыми базовыми вариантами использования для классификации и кластеризации. Это поможет нам понять использование метрик расстояния в моделировании машинного обучения. Мы начнем с быстрого введения контролируемых и неконтролируемых алгоритмов и постепенно перейдем к примерам.

Видео:Длина отрезкаСкачать

1. Классификация

K-Ближайшие соседи (KNN) —

KNN — это не вероятностный контролируемый алгоритм обучения, т.е. он не дает вероятности принадлежности к какой-либо точке данных, а KNN классифицирует данные при жестком назначении, например, точка данных будет принадлежать 0 или 1. Теперь вы должны подумать как работает KNN, если не используется уравнение вероятности. KNN использует метрики расстояния, чтобы найти сходства или различия.

Давайте возьмем набор данных iris, который имеет три класса, и посмотрим, как KNN будет определять классы для тестовых данных.

На изображении № 2 над черным квадратом находится тестовая точка данных. Теперь нам нужно найти, к какому классу относится эта контрольная точка данных, с помощью алгоритма KNN. Теперь мы подготовим набор данных для создания модели машинного обучения, чтобы предсказать класс для наших тестовых данных.

В алгоритме классификации КНН мы определяем постоянную«K».K — количество ближайших соседей контрольной точки данных. Эти K точек данных затем будут использоваться для определения класса для точки тестовых данных (обратите внимание, что это в наборе обучающих данных).

Вам интересно, как бы мы нашли ближайших соседей. Ну вот где метрика расстояния входит в картинки. Сначала мы рассчитываем расстояние между каждым поездом и контрольной точкой данных, а затем выбираем ближайшую вершину в соответствии со значением k.

Мы не будем создавать KNN с нуля, но будем использовать scikit KNN классификатор

Как видно из приведенного выше кода, мы используем метрику расстояния Минковского со значением p, равным 2, то есть в классификаторе KNN будет использоваться формула Евклидовой метрики расстояния.

По мере продвижения вперед в моделировании машинного обучения мы можем теперь обучать нашу модель и начинать предсказывать класс для тестовых данных.

Как только верхние ближайшие соседи выбраны, мы проверяем большинство проголосовавших классов в соседях —

Из приведенного выше изображения, вы можете угадать класс для контрольной точки? Это класс 1, так как он является самым популярным.

Из этого небольшого примера мы увидели, какметрика расстояниябыл важен для классификатора KNN.Это помогло нам получить самые близкие точки данных поезда, для которых были известны классы.Существует вероятность, что при использовании различных метрик расстояния мы могли бы получить лучшие результаты. Таким образом, в не вероятностном алгоритме, таком как KNN, метрики расстояния играют важную роль.

Видео:19. Расстояние между параллельными прямыми Расстояние между скрещивающимися прямымиСкачать

2. Кластеризация

K-нуждаемость

В алгоритмах классификации, вероятностных или не вероятностных, нам будут предоставлены помеченные данные, что упрощает прогнозирование классов. Хотя в алгоритме кластеризации у нас нет информации о том, какая точка данных принадлежит какому классу. Метрики расстояния являются важной частью этого вида алгоритма.

В K-средних мы выбираем количество центроидов, которые определяют количество кластеров.Затем каждая точка данных будет привязана к ближайшему центроиду, используя метрику расстояния (евклидово), Мы будем использовать данные радужной оболочки, чтобы понять основной процесс K-средних.

На приведенном выше изображении № 1, как вы можете видеть, мы случайно разместили центроиды, а на рисунке № 2, используя метрику расстояния, пытались найти ближайший класс кластеров.

Нам нужно будет повторять назначение центроидов до тех пор, пока у нас не будет четкой кластерной структуры.

Как мы видели в приведенном выше примере, не имея никаких знаний о метках с помощью метрики расстояния в K-средних, мы разбили данные на 3 класса.

Видео:РАССТОЯНИЕ МЕЖДУ ТОЧКАМИ 10 и 11 классСкачать

3. Обработка естественного языка

Поиск информации

В поиске информации мы работаем с неструктурированными данными. Данные могут быть статьей, веб-сайтом, электронной почтой, текстовыми сообщениями, публикацией в социальных сетях и т. Д. С помощью методов, используемых в НЛП, мы можем создавать векторные данные таким образом, чтобы их можно было использовать для получения информации при запросе. Как только неструктурированные данные преобразуются в векторную форму, мы можем использовать метрику косинусного сходства, чтобы отфильтровать ненужные документы из корпуса.

Давайте возьмем пример и поймем использование косинусного сходства.

1. Создать векторную форму для Корпуса и Query-

2. Проверьте сходства, т.е. найдите, какой документ в корпусе имеет отношение к нашему запросу.

Как видно из приведенного выше примера, мы запросили слово«Коричневый»и в корпусе есть только три документа, которые содержат слово«Коричневый».При проверке с помощью косинусной метрики сходства он дал те же результаты, имея> 0 значений для трех документов, кроме четвертого

Видео:Расстояние между скрещивающимися прямымиСкачать

Вывод

В этой статье мы узнали о нескольких популярных метриках расстояния / сходства и о том, как их можно использовать для решения сложных задач машинного обучения. Надеюсь, что это будет полезно для людей, которые только начинают изучать машинное обучение и науку о данных.

Видео:A.7.38 Расстояние МахаланобисаСкачать

Евклидова, L1 и Чебышёва — 3 основные метрики, которые пригодятся в Data Science

Не важно, начинаете вы осваивать Data Science или работаете в этой сфере не первый год, вам наверняка пригодятся эти метрики. Разбираемся, что они из себя представляют и чем отличаются друг от друга.

Видео:Определение расстояние между параллельными прямыми (Способ замены плоскостей проекции).Скачать

Евклидово расстояние (расстояние по прямой)

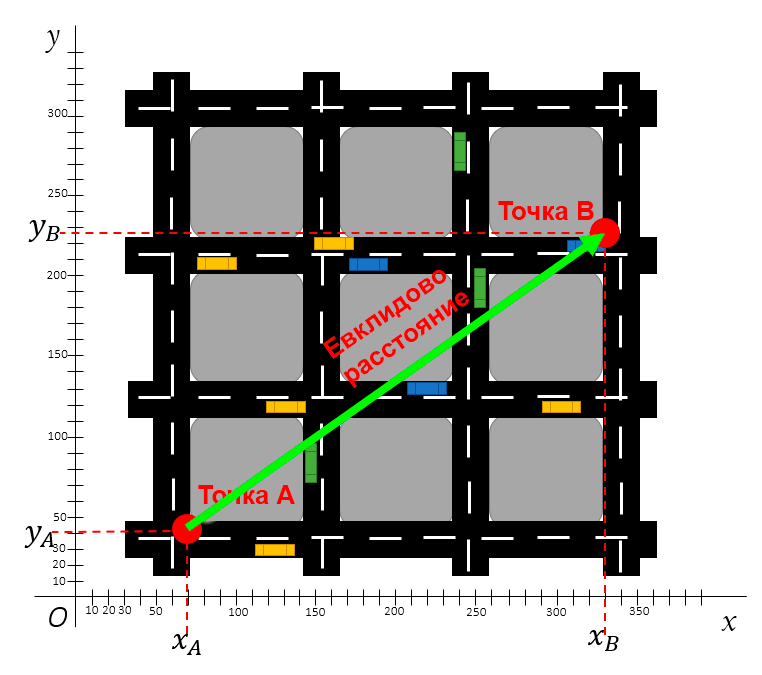
Евклидово расстояние самое интуитивное для понимания: именно Евклидову метрику мы представляем, когда кто-то просит нас измерить расстояние между точками.

Евклидово расстояние — это прямая линия между двумя точками с координатами X и Y. Например, одной из таких точек может быть город на карте с его координатами долготы и широты.

Евклидово расстояние характеризуется прямой линией. Допустим, вам нужно измерить расстояние по прямой между точками A и B на карте города, приведённой ниже.

Евклидово расстояние между двумя точками считается по теореме Пифагора

Для расчёта Евклидового расстояния вам понадобятся лишь координаты этих двух точек. Дистанцию между ними можно будет рассчитать по формуле Пифагора.

Sportmaster Lab , Санкт-Петербург, Липецк, Москва , От 120 000 до 350 000 ₽

Теорема Пифагора гласит, что можно рассчитать длину «диагональной стороны» (гипотенузы) прямого треугольника, зная длины его горизонтальной и вертикальной стороны (катетов). Формула выглядит так: a² + b² = c².

Пример расчёта Евклидового расстояния

Прим. ред. В четвёртой строке вычислений допущена ошибка: (-260)^2 = 67 600, а не 76 600. Тогда результат будет равен

Видео:Экзотические метрики и их примененияСкачать

Расстояние L1 (расстояние городских кварталов)

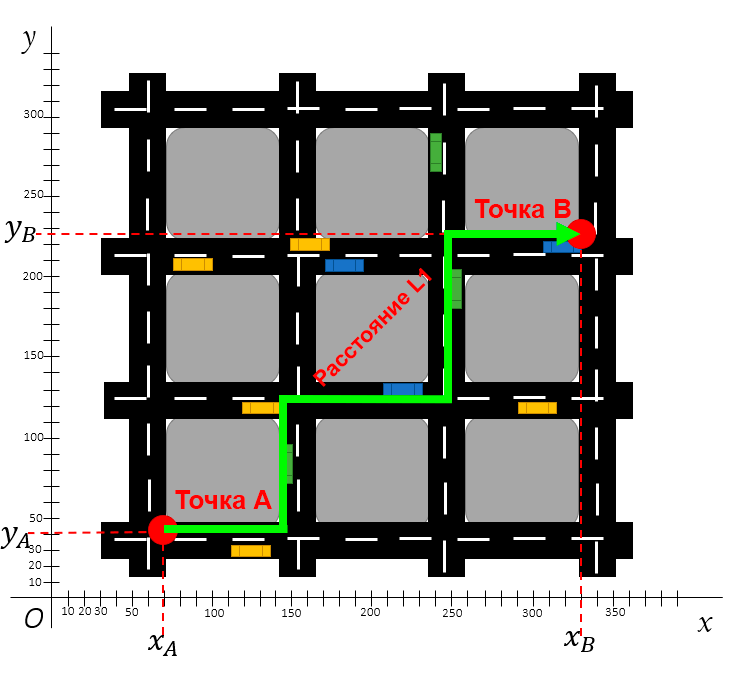
Расстояние L1 также известно как расстояние городских кварталов, манхэттенское расстояние, расстояние такси, метрика прямоугольного города — оно измеряет дистанцию не по кратчайшей прямой, а по блокам. Расстояние L1 измеряет дистанцию между городскими блоками: это расстояние всех прямых линий пути.

На следующем изображении показано расстояние L1 между двумя точками.

Расстояние L1 между двумя точками по блокам

Кроме показанного пути существует несколько альтернативных способов. Например, от точки A можно подняться на два блока вверх, а потом на три блока вправо, либо же на три блока вправо и два блока вверх.

Но расстояние L1 — это всё же просто дистанция, а поэтому траектория здесь не имеет значения. Единственное, что нужно понимать, это примерный путь: нужно пройти какое-то количество X блоков на восток и Y блоков на север. Сумма расстояний этих блоков и будет расстоянием L1 от точки A до точки B.

Пример расчёта расстояния L1 между двумя точками

Видео:Расстояние между двумя точками. Координаты середины отрезка.Скачать

Расстояние Чебышёва (метрика шахматной доски)

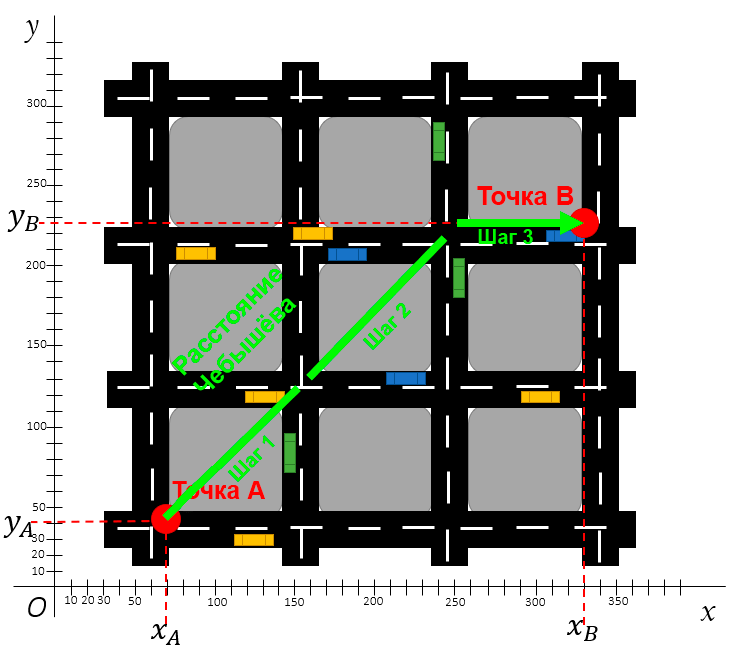
Расстояние Чебышёва известно ещё как расстояние шахматной доски. Чтобы понять принцип такой метрики, нужно представить короля на шахматной доске — он может ходить во всех направлениях: вперёд, назад, влево, вправо и по диагонали.

Расстояние Чебышёва между двумя точками

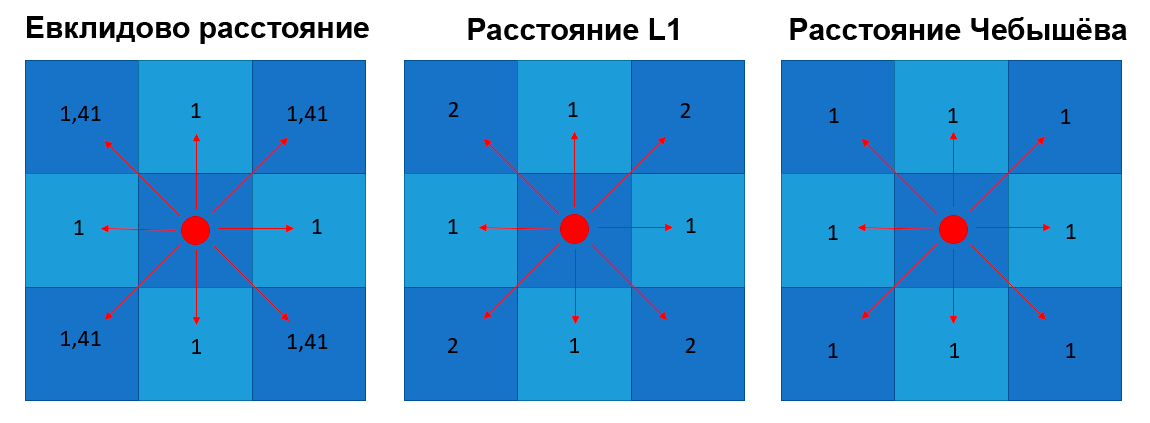
Разница расстояния L1 и расстояния Чебышёва в том, что при переходе на одну клетку по диагонали в первом случае засчитывается два хода (например вверх и влево), а во втором случае засчитывается всего один ход.

Ещё эти оба расстояния отличаются от Евклидового расстояния тем, что у Евклидового движение по диагонали рассчитывается по теореме Пифагора.

Сравнение путей 3 метрик

Расстояние Чебышёва можно представить как проход по шахматной доске.

Вот ещё один пример представления расстояния Чебышёва. Допустим, у вас есть дрон с двумя независимыми моторами: первый мотор тянет дрон вперёд, второй — в сторону. Оба мотора могут работать одновременно и равномерно на максимуме своей мощности.

Поэтому дрон может передвинуться на одну клетку по диагонали так же быстро, как по горизонтали или вертикали.

Посмотрите ещё раз на карту города по расстоянию Чебышёва. Первый шаг — оба мотора работают одновременно, второй шаг идентичен первому, а на третьем шаге мотор, тянущий дрон вперёд, отключается, и дрон смещается в сторону.

Таким образом, расстояние Чебышёва определяется как самая большая дистанция на одной оси.

Пример расчёта расстояния Чебышёва между двумя точками

Прим. ред. Полученный результат является условным и некорректно сравнивать его с другими результатами.

Видео:Уравнение окружности и формула расстояния между точками на плоскостиСкачать

Расстояние Махаланобиса

Видео:Расстояние между скрещивающимися прямыми #2Скачать

Содержание

Если есть замечания или ошибки, пишите на почту quwarm@gmail.com или в комментариях.

Видео:Стереометрия ЕГЭ. Метод координат. Часть 5 из 5. Расстояние между прямымиСкачать

Основной смысл использования расстояния Махаланобиса

На рисунке 1 два наблюдения изображены в виде красных точек.
Центр класса изображен в виде синей точки.

Рисунок 1. Двумерные данные с эллипсами прогноза

Вопрос — какое наблюдение ближе к центру класса?
Ответ зависит от того, как измеряется расстояние.

Если измерять расстояние по метрике Евклида, то получим, что расстояние от центра класса до точки равно , до точки равно , т. е. точка ближе к центру класса.

Однако для этого распределения дисперсия в направлении меньше, чем дисперсия в направлении , поэтому в некотором смысле точка находится «на большем стандартном отклонении» от центра класса, чем .

Эллипсы прогноза, изображенные на рисунке, подсказывают, что точка ближе по распределению, чем точка . Измерив расстояние по Махаланобису, получим, что расстояние от центра класса до точки примерно равно , до точки примерно равно , т. е. точка ближе к центру класса. В этом и заключается основной смысл использования метрики Махаланобиса — учитывание дисперсий и ковариаций.

Кроме того, расстояние Махаланобиса предполагает, что точки множества эллипсоидально (частный случай — сферически) распределены вокруг центра масс.

Видео:"Парадоксальное" среднее расстояние между точками на окружностиСкачать

1. Термины и определения

Метрика — функция, определяющая расстояние между любыми точками в метрическом пространстве , где — размерность пространства.

Класс — конечное неупорядоченное множество схожих по некоторым критериям оптимальности точек: , где — количество точек в классе .

Точка — конечное упорядоченное множество значений признаков: .

Будем обозначать буквой число признаков, а буквой — признак.

Под словом «точка» подразумевается точка координатного -мерного пространства признаков. Причем замеченные сходства и различия между точками находятся в соответствии с расстояниями между ними.

Классы и точки в статье обозначаются как вектор-строки. В литературе и Интернете они иногда обозначаются как вектор-столбцы — тогда в некоторых частях формул операция транспонирования убирается, а в других добавляется.

В примерах: признак точки из класса обозначается как .

Подразумевается, что одинаковых точек в классе (-ах) нет.

Видео:#31. Как найти расстояние между скрещивающимися прямыми?Скачать

2. Расстояние Махаланобиса между двумя точками и между точкой и классом

Этот пункт включает внутриклассовое расстояние (расстояние между двумя точками из одного класса) и расстояние между точкой (не принадлежащей ни одному из классов) и классом.

2.1 Теоретические сведения

Расстояние Махаланобиса между двумя точками — мера расстояния между двумя случайными точками и , одна из которых может (или обе могут ) принадлежать некоторому классу с матрицей ковариаций :

Символ означает операцию транспонирования, а под подразумевается матрица, обратная ковариационной.

Если матрица ковариаций является единичной матрицей, то расстояние Махаланобиса становится равным расстоянию Евклида.
Иначе говоря, если класс представляет собой упорядоченное множество нормированных (дисперсии равны 1) независимых (ковариации равны 0) точек, то расстояние Махаланобиса равно расстоянию Евклида.

Расстояние Махаланобиса является метрикой (доказательство здесь [internet archive] и здесь), т. е. между двумя точками и с матрицей ковариаций в пространстве признаков удовлетворяет следующим аксиомам:
1. Аксиома тождества: ;
2. Аксиома симметрии: ;
3. Аксиома треугольника: .
Из этих аксиом следует неотрицательность функции расстояния: .

Из аксиом следует, что значение под корнем не меньше 0, однако при расчетах с использованием неточных вещественных чисел рекомендуется предварительно ограничивать диапазон результата слева значением 0 ( max(0.0, value) ) во избежание NaN, которое появляется после взятия корня (функция sqrt или возведение в степень 0.5 ) близкого к 0 слева числа (например, ). Этот нюанс часто не замечается.

Чтобы найти внутриклассовое расстояние Махаланобиса, нужно следовать вышеприведенной формуле — вычислить матрицу ковариаций класса и затем само расстояние между двумя точками в нем.

Чтобы найти расстояние Махаланобиса между точкой (не принадлежащей ни одному из классов) и классом, нужно также следовать вышеприведенной формуле — вычислить матрицу ковариаций класса и затем расстояние между точкой (не принадлежащей ни одному из классов) и центроидом класса (т. н. «расстояние до центроида»).

Для решения задачи классификации тестовой точки, нужно найти матрицы ковариаций всех классов. Затем с помощью подсчета расстояний от заданной точки до каждого класса выбрать класс, до которого расстояние минимально.
Некоторые методы (такие, как метод -ближайших соседей, который будет рассмотрен в п. 4) подразумевают вычисление расстояний не до центроидов классов, а до всех точек всех классов.

Перед тем, как находить матрицу ковариаций, необходимо вычислить математические ожидания* точек класса по признакам.

На практике математическое ожидание обычно оценивается как среднее арифметическое:

где — среднее арифметическое точек класса по признаку, — количество точек в классе , — признак точки .

Центроид класса :

Ковариация — это численное выражение свойства ковариантности двух признаков точек.
Свойство ковариантности означает, что признаки имеют тенденцию изменяться совместно (ковариантно).

Ковариационная матрица состоит из ковариаций между всеми парами признаков. Если количество признаков равно , то ковариационная матрица — матрица размерности , имеющая вид:

Элементы ковариационной матрицы — ковариации — для набора точек вычисляются по формуле (несмещенная ковариация, англ. «sample covariance»):

где и — математические ожидания по и признакам точек соответственно, — количество точек в классе .

Формулу нужно использовать только в том случае, если математические ожидания генеральной совокупности и рассматриваемого класса неизвестны. Если же они известны, то формула имеет вид (смещенная ковариация, англ. «population covariance»):

Ковариация обладает следующими важными свойствами:

Если при переходе от одной точки к другой и признаки увеличиваются (уменьшаются) вместе, то 0″ alt=»cov_>0″ src=»https://habrastorage.org/getpro/habr/upload_files/faf/07a/9e9/faf07a9e95c345f811620c58ea69f13b.svg»/>;

Если при переходе от одной точки к другой признак увеличивается, а уменьшается (или наоборот), то ;

Если при переходе от одной точки к другой и признаки изменяются независимо, то (обратное утверждение в общем случае неверно*).

Ковариация симметрична: .

Неравенство Коши — Буняковского: .

Пусть — равномерно распределенная случайная величина в и .
и зависимы, но:

где — математическое ожидание.

Первые три свойства ковариации проиллюстрированы на рисунке 2.

Рисунок 2. Знак ковариации двух случайных величин X и Y

Так как для вычисления метрики Махаланобиса требуется найти обратную к матрицу, а матрица обратима тогда и только тогда, когда она является квадратной и невырожденной (определитель не равен нулю), то необходимо и достаточно, чтобы определитель матрицы не равнялся нулю. Однако такое требование является серьезным ограничением.

Известно, что ковариационная матрица необратима в следующих частных случаях:
1. Если по какому-либо признаку все точки класса имеют одно и то же значение и, следовательно, среднеквадратическое отклонение по признаку равно нулю.
Пример: .
2. Если ковариации всех признаков максимальны (, «perfect covariance»). Примеры:
— идеальная положительная ковариация;
— идеальная отрицательная ковариация.
3. Если количество точек в классе меньше количества признаков плюс :

Есть и другие случаи.

Что делать, если ковариационная матрица необратима?
Единственно правильного подхода не существует.
Однако существует целая область исследований, направленная на регуляризацию этой проблемы.
Три приведенные выше и некоторые другие проблемы могут быть решены следующими способами:

1. Два способа для первого случая

Добавить больше точек в класс, чтобы среднеквадратическое отклонение (аналогично — дисперсия) по признаку не равнялось нулю.

Убрать признак из рассмотрения.

Использовать модификацию метрики Махаланобиса (например, для второго случая), — метрику Евклида-Махаланобиса (из статьи):

где — единичная матрица того же размера, что и .

Эта метрика устраняет недостаток метрики Махаланобиса, поскольку элементы её главной диагонали всегда больше нуля.

Помимо обратной матрицы существует псевдообратная матрица.
Операция — псевдообратное преобразование матрицы (обратное преобразование Мура — Пенроуза).
Функции вычисления псевдообратной матрицы:
— ginv в библиотеке MASS (R);
— pinv в библиотеке numpy (Python);
— pinv в MATLAB;
— pinv в Octave.

Псевдообратная матрица, обозначаемая , (в отрыве от темы статьи) определяется как матрица, которая «решает» задачу наименьших квадратов: , где — прямоугольная матрица, в которой число строк (уравнений) больше числа столбцов (переменных); такая система уравнений в общем случае не имеет решения, поэтому эту систему можно «решить» только в смысле выбора такого вектора , чтобы минимизировать «расстояние» между векторами и .
Псевдообратная матрица может быть найдена с помощью сингулярного разложения матрицы. Причем для любой матрицы над вещественными числами существует псевдообратная матрица и притом только одна.
Также важно отметить тот факт, что если обратную матрицу можно найти (иначе говоря, исходная матрица — квадратная и невырожденная), то псевдообратная будет с совпадать: .

Формула вычисления расстояния:

Псевдообратный подход иногда применяют в расстоянии Махаланобиса, но: «Мы получаем значительно меньшую точность классификации при использовании псевдообратных матриц. Действительно, псевдообратный подход генерирует вдвое больше ошибок, чем метод усадки ковариационной матрицы или метод диагональной матрицы» (из статьи).

Кроме того, далее будет продемонстрирован случай, когда при использовании псевдообратного подхода нарушается аксиома тождества (из-за чего этот подход называют псевдорасстоянием Махаланобиса или псевдометрикой).

Метод усадки (shrinkage) ковариационной матрицы — это метод оценки задач с небольшим количеством точек и большим количеством признаков (т. е. для третьего случая).
Смысл этого метода в замене матрицы на матрицу, где — некоторая подходящая положительно определенная матрица, — коэффициент усадки, причем наименьшее собственное значение матрицы должно быть не меньше , умноженной на наименьшее собственное значение .
В расстоянии Махаланобиса:

Предложение Olivier Ledoit и Michael Wolf — , где — сумма диагональных элементов матрицы , деленная на число признаков, — единичная матрица, а вычисляется в соответствии с приведенным авторами алгоритмом.
Реализация алгоритма, предложенного авторами, на Python имеется в библиотеке scikit-learn (sklearn.covariance.LedoitWolf, sklearn.covariance.ledoit_wolf, sklearn.covariance.ledoit_wolf_shrinkage).

На стр. 8 написано, что «в отличие от псевдообратного подхода, метод усадки ковариационной матрицы генерирует обобщенную меру расстояния, которая является метрикой» (адаптированный перевод). Это утверждение может ввести в заблуждение в отрыве от контекста — три перечисленных выше условия (про , про , про собственные значения) обязательны, иначе результат может быть неверным.
Следующий пример демонстрирует несоблюдение условия .

Пусть , тогда в соответствии с предложением в этой и этой статьях (реализация на Python):
— ;
— расстояние от точки до точки : ;
— расстояние от точки до точки : ;
— расстояние от точки до точки : ;
— расстояние от точки до точки : .
В данном случае предложение:

где — диагональная матрица со значениями на диагонали .

Также есть Shrunk Covariance (sklearn.covariance.ShrunkCovariance, sklearn.covariance.shrunk_covariance). Однако он не находит , а предлагает пользовательский выбор (по умолчанию ).
Матрица (как и в предложении Ledoit — Wolf): .

Общую информацию об усадке можно почитать в википедии.

Причем стоит обратить внимание на то, что LedoitWolf и ShrunkCovariance (и некоторые другие методы) используют empirical_covariance, которая вычисляет смещенную ковариацию (англ. «population covariance», формула ).

Если матрица ковариаций диагональная (но необязательно единичная), то получившаяся мера расстояния носит название «нормализованное расстояние Евклида»:

где — среднеквадратическое отклонение точек класса (к которому относится точка и/или точка ) по признаку (исправленное СКО, «corrected sample standard deviation»):

где — математическое ожидание точек класса к которому относится точка и/или точка ) по признаку.
В случае среднего арифметического:

Формулу нужно использовать только в том случае, если математические ожидания генеральной совокупности рассматриваемого класса неизвестны. Если же они известны, то формула имеет вид (неисправленное СКО, англ. «uncorrected sample standard deviation»):

Это расстояние не учитывает какую-либо зависимость между признаками и требует не равные нулю среднеквадратические отклонения.

Или более полно:

Это расстояние не учитывает какую-либо зависимость между признаками и требует не равные нулю среднеквадратические отклонения.

Есть и другие способы, но они выходят за рамки этой статьи.

Во всяком случае, как показывает практика, нужно использовать примерно в 10 раз больше точек, чем признаков. Ведь задача не только в том, чтобы ковариация была хорошо обусловлена, но также и в том, чтобы она была точной.

2.2 Алгоритм вычисления расстояния между двумя точками и между точкой и классом

Шаг 1. Вычислить математические ожидания значений признаков точек класса.

Шаг 2. Вычислить среднеквадратические отклонения значений признаков точек класса.

Шаг 3. Вычислить ковариации между всеми парами признаков точек класса и составить ковариационную матрицу.

Шаг 4. Если матрица обратима, то вычислить расстояние по Махаланобису. Если нет, то попробовать один из вышеперечисленных способов решения.

2.3 Пример вычисления расстояния между двумя точками и между точкой и классом

Пусть имеется тестовая точка и два следующих класса (рис. 3):

Рисунок 3. Исходные данные примера

Шаг 1. Вычислим математические ожидания значений признаков точек классов.

Шаг 2. Вычислим среднеквадратические отклонения значений признаков точек классов.

По первому и второму признакам точек первого класса:

По первому и второму признакам точек второго класса:

Шаг 3. Вычислим ковариации между всеми парами признаков точек классов и составим ковариационные матрицы.

Для первого класса.

Получим следующую матрицу ковариаций:

Вычислим определитель этой матрицы: . Следовательно, матрица необратима.

Для второго класса.

Получим следующую матрицу ковариаций:

Вычислим определитель этой матрицы: . Следовательно, матрица обратима.

Код на Python 3.6 с использованием библиотеки numpy 1.19.5

Шаг 4. Если матрица обратима, то вычислим расстояние по Махаланобису и расстояние по Евклиду — Махаланобису. Если матрица необратима, то попробуем несколько способов решения этой проблемы.

Различают расстояние, измеряемое по принципу ближайшего соседа, дальнего соседа и расстояние, измеряемое по принципу центроида.
Измерим расстояния между тестовой точкой и всеми точками классов, включая точку центроида.

Первый класс. Как уже было сказано ранее — для матрицы ковариаций первого класса нельзя найти обратную матрицу, поэтому расстояние между тестовой точкой и первым классом будем вычислять по 5 формулам: (1) метрика Евклида — Махаланобиса, (2) метод усадки ковариационной матрицы (LedoitWolf), (3) псевдообратный подход, (4) нормализованное расстояние Евклида, (5) метод диагональной матрицы — и выберем среди них наиболее правдоподобную:

1. Метрика Евклида — Махаланобиса.

Код на Python 3.6 с использованием библиотеки numpy 1.19.5

Первая точка — точка центроида, которая совпадает с одной из точек класса.

2. Метод усадки ковариационной матрицы (LedoitWolf).

Код на Python 3.6 с использованием библиотек numpy 1.19.5 и scikit-learn 0.24.1

Первая точка — точка центроида, которая совпадает с одной из точек класса.

3. Псевдообратный подход.

Ранее уже было сказано про псевдообратные матрицы. Их недостаток использования демонстрируется в следующем примере.

Как видим, нарушена аксиома тождества — расстояние между двумя различными точками равно нулю.

Код на Python 3.6 с использованием библиотеки numpy 1.19.5

Первая точка — точка центроида, которая совпадает с одной из точек класса.

4. Нормализованное расстояние Евклида.

Код на Python 3.6 с использованием библиотеки numpy 1.19.5

Первая точка — точка центроида, которая совпадает с одной из точек класса.

5. Метод диагональной матрицы.

Код на Python 3.6 с использованием библиотеки numpy 1.19.5

Первая точка — точка центроида, которая совпадает с одной из точек класса.

Второй класс. Для матрицы ковариаций второго класса можно найти обратную матрицу (это можно сделать несколькими способами). Вручную легче всего вычислять при помощи матрицы алгебраических дополнений:

где — определитель матрицы , — транспонированная матрица алгебраических дополнений для матрицы ковариаций второго класса.

Код на Python 3.6 с использованием библиотеки numpy 1.19.5

Первая точка — точка центроида.

• По принципу ближнего соседа

Первый класс:
1. Метрика Евклида — Махаланобиса: ;
2. Метод усадки ковариационной матрицы (LedoitWolf): ;
3. Псевдообратный подход: ;
4. Нормализованное расстояние Евклида: ;
5. Метод диагональной матрицы: .

Второй класс (метрика Махаланобиса): .
Второй класс (метрика Евклида — Махаланобиса): .

Судя по рисунку 3, более правдоподобны (для данного примера и принципа) метрика Евклида — Махаланобиса, метод усадки ковариационной матрицы и метод диагональной матрицы.

• По принципу дальнего соседа

Первый класс:
1. Метрика Евклида — Махаланобиса: ;
2. Метод усадки ковариационной матрицы (LedoitWolf): ;
3. Псевдообратный подход: ;
4. Нормализованное расстояние Евклида: ;
5. Метод диагональной матрицы: .

Второй класс (метрика Махаланобиса): .
Второй класс (метрика Евклида — Махаланобиса): .

Судя по рисунку 3, более правдоподобны (для данного примера и принципа) метод усадки ковариационной матрицы и метод диагональной матрицы.

• По принципу центроида

Первый класс:
1. Метрика Евклида — Махаланобиса: ;
2. Метод усадки ковариационной матрицы (LedoitWolf): ;
3. Псевдообратный подход: ;
4. Нормализованное расстояние Евклида: ;
5. Метод диагональной матрицы: .

Второй класс (метрика Махаланобиса): .
Второй класс (метрика Евклида — Махаланобиса): .

Судя по рисунку 3, более правдоподобны (для данного примера и принципа) метрика Евклида — Махаланобиса, метод усадки ковариационной матрицы и метод диагональной матрицы.

Результат

Наиболее правдоподобными методами для данного примера являются метод усадки ковариационной матрицы и метод диагональной матрицы.

3. Расстояние Махаланобиса между двумя классами

Этот пункт включает расстояние между двумя классами и расстояние между точкой (представляющей единственный объект класса) и классом.

Расстояние Махаланобиса между двумя классами является квазиметрикой, т. е.:
— удовлетворяет условиям , , .
— не удовлетворяет условию (в общем случае) .
Подробнее здесь.

3.1 Теоретические сведения

Расстояние Махаланобиса между двумя классами — мера расстояния между двумя классами и с центроидами и и с матрицами ковариаций и соответственно:

где — объединенная ковариационная матрица, — обратная объединенная ковариационная матрица, и — матрицы ковариаций двух классов, и — число точек в первом и во втором классах соответственно.

Причем в некоторой литературе также предлагается другой вариант:

Важно выбрать и применять только один из этих двух вариантов.
Кроме того, следует всегда отмечать, какой из вариантов используется.

Примечательно то, что при использовании второго варианта для первого класса с одной точкой и некоторого второго класса получается формула, аналогичная формуле расчета расстояния между точкой (не принадлежащей ни одному из классов) и классом (п. 2 «Расстояние Махаланобиса между двумя точками и между точкой и классом»):

Расстояние Евклида-Махаланобиса между двумя классами:

где — единичная матрица того же размера, что и .

3.2 Алгоритм вычисления расстояния между двумя классами

Шаг 1. Вычислить математические ожидания значений признаков точек классов.

Шаг 2. Вычислить среднеквадратичные отклонения значений признаков точек классов.

Шаг 3. Вычислить ковариации между всеми парами признаков точек классов, составить ковариационные матрицы и объединенную ковариационную матрицу.

Шаг 4. Если матрица обратима, то вычислить расстояние по Махаланобису. Если матрица необратима, то вычислить расстояние по формуле расстояния Евклида — Махаланобиса.

3.3 Пример вычисления расстояния между двумя классами

Из примера п. 2.2.

Найдем расстояние между двумя классами.
Первые 3 аналогичных шага алгоритма были выполнены в п. 2.2.
Выполним 4 шаг.

Шаг 4. Если матрица обратима, то вычислим расстояние по Махаланобису. Если матрица необратима, то вычислим расстояние по формуле расстояния Евклида — Махаланобиса.

Объединенная ковариационная матрица:

Обратная объединенная ковариационная матрица:

• По принципу центроида

Расстояние Махаланобиса.

Расстояние Евклида — Махаланобиса .

Для варианта :
— расстояние Махаланобиса ;
— расстояние Евклида — Махаланобиса .

• По принципу ближнего соседа

Минимальное расстояние Махаланобиса между и и между и .

Минимальное расстояние Евклида — Махаланобиса между и и между и .

Для варианта :
— минимальное расстояние Махаланобиса между и и между и ;
— минимальное расстояние Евклида — Махаланобиса между и и между и .

• По принципу дальнего соседа

Максимальное расстояние Махаланобиса между и и между и .

Максимальное расстояние Евклида — Махаланобиса между и и между и .

Для варианта :
— максимальное расстояние Махаланобиса между и и между и ;
— максимальное расстояние Евклида — Махаланобиса между и и между и .

Код на Python 3.6 с использованием библиотеки numpy 1.19.5 для расчета представлен здесь.

4. Расстояние Махаланобиса и метод k-ближайших соседей

Классифицировать тестовую точку можно при помощи метода -ближайших соседей. Сначала нужно вычислить ковариационную матрицу для каждого класса, затем определить -ближайших соседей для тестовой точки (вычислив расстояния от неё до всех точек всех классов с учетом ковариационных матриц) и отнести точку к классу с наибольшим количеством вхождений среди ближайших соседей.

Далее представлен код программы для классификации методом -ближайших соседей.
Причем:
— Обратная матрица: (метрика Евклида — Махаланобиса);
— Используется квадрат расстояния (квадратный корень не имеет значения для конечного результата классификации, а без него программа работает немного быстрее).

Код на Python 3.6 с использованием библиотеки numpy 1.19.5

Вывод программы в формате:
«knn: [наименьший номер класса (с 1), к которому можно отнести точку] [вероятностные оценки для тестовых точек для всех классов] [индексы классов (с 0), к которым можно отнести точку]».

Визуализация классификации сетки точек при разных значениях представлена на рис. 4.

Рисунок 4. Визуализация классификации сетки точек Код для визуализации на Python 3.6

Один запуск — один график для аргумента .

5. Взвешенное расстояние Махаланобиса

Расширением понятия расстояния Махаланобиса является взвешенное расстояние Махаланобиса, формула которой отличается от последней наличием дополнительного сомножителя — симметрической неотрицательно определенной матрицы весовых коэффициентов , недиагональные элементы которой чаще всего равны нулю:

Пример матрицы весовых коэффициентов (является единичной, поэтому на результат не повлияет) для точек с двумя признаками:

Формула взвешенного расстояния Евклида — Махаланобиса:

6. Заключение

В статье даны определения расстояний и метрик Махаланобиса, приведены теоретические сведения и рассмотрены примеры вычисления расстояний между двумя точками (также между точкой и классом) и между двумя классами, написана программа для классификации по методу -ближайших соседей с использованием метрики Евклида — Махаланобиса.

Что ещё?
1. Существует полиномиальное расстояние Махаланобиса, о котором можно почитать здесь.
2. О применении расстояния Махаланобиса в машинном обучении можно почитать в книге «Metric Learning» (авторы: Aurélien Bellet, Amaury Habrard, Marc Sebban; версия для ознакомления).
3. Расстояние Махаланобиса может использоваться в кластеризации (например, k-means: статья 1, статья 2, статья 3).
4. Расстояние Махаланобиса может использоваться в области интеллектуального анализа текста (статья).
5. Расстояние Махаланобиса может использоваться для обнаружения выбросов (статья 1, статья 2, статья 3).