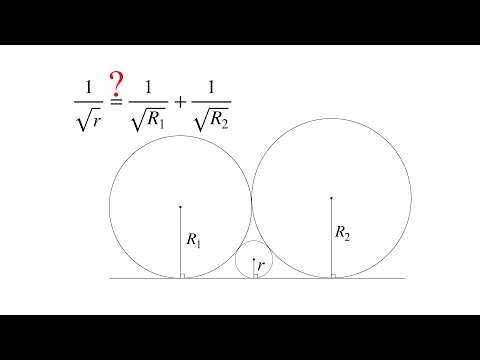
Две касающиеся внешним образом в точке K окружности, радиусы которых равны 16 и 48, вписаны в угол с вершиной A. Общая касательная к этим окружностям, проходящая через точку K, пересекает стороны угла в точках B и C. Найдите радиус окружности, описанной около треугольника ABC.
Пусть Q — центр большей окружности, а O — центр меньшей, QM и ON — радиусы, проведённые в точки касания окружностей с прямой AC, S — центр окружности, описанной около треугольника ABC , r — радиус окружности, описанной около треугольника ABC .
Поскольку BC и AB — общие касательные к окружностям, BO и BQ — биссектрисы углов ABK и смежного с ним. Значит, угол OBQ прямой, следовательно, из треугольника OBQ находим, что
Пусть AN = x. Прямоугольные треугольники ANO и AMQ подобны с коэффициентом 3, значит, AM = 3x , MN = 2x.
Отрезки MC , CK и CN равны как отрезки касательных, проведённых из одной точки, значит, ,
, откуда
.
В прямоугольном треугольнике ABK находим неизвестный катет:
В прямоугольном треугольнике SBK по теореме Пифагора имеем
;
Приведем примечание Киры Ананьиной.
Заменим, что в прямоугольном треугольнике ABK следовательно, угол BAK равен 30 градусов, а угол BAC равен 60 градусов. Следовательно, треугольник ABC равносторонний, и центр описанной вокруг него окружности совпадает с центром вписанной в него окружности. Таким образом, точки S и O совпадут.
Видео:Две касающиеся внешним образом в точке А окружности, радиусы которых равны 4 и 8Скачать

Задание 16 Профильного ЕГЭ по математике. Планиметрия. Задача 3
Две окружности касаются внешним образом в точке K. Прямая AB касается первой окружности в точке A, а второй — в точке B. Прямая BK пересекает первую окружность в точке D, прямая AK пересекает вторую окружность в точке C
а) Докажите, что прямые AD и BC параллельны.
б) Найдите площадь треугольника AKB, если известно, что радиусы окружностей равны 4 и 1.
а) Другими словами, в пункте (а) надо доказать, что точка D лежит на прямой , а точка C — на прямой .
— прямоугольная трапеция, поскольку (как радиусы, проведенные в точку касания), .
Если , то (как односторонние углы),
Тогда — диаметр первой окружности; — диаметр второй окружности, так как вписанный угол, опирающийся на диаметр, — прямой.
AK — высота в , где
Рассмотрев прямоугольную трапецию , где , найдем, что .
Видео:Две окружности | Резерв досрока ЕГЭ-2019. Задание 16. Профильный уровень | Борис Трушин |Скачать

Задача 45619 Две касающиеся внешним образом в точке К.
Условие
Две касающиеся внешним образом в точке К окружности, радиус одной из которых вдвое больше радиуса другой, вписаны в угол с вершиной А. Общая касательная к этим окружностям, проходящая через точку К, пересекает стороны угла в точках В и С.
а) Докажите, что АВ = АС.
б) Найдите радиус окружности, описанной около треугольника АВС, если АВ = sqrt(3). [16п2]
Все решения
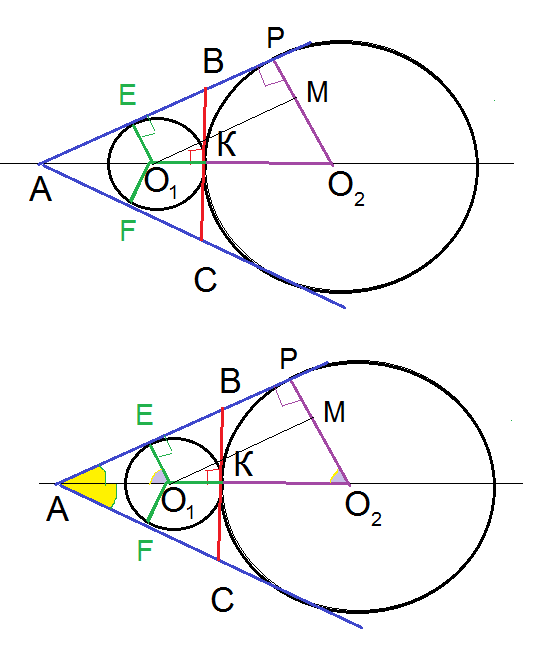
Две окружности вписаны в угол с вершиной А.
Радиусы O_(1)E и O_(1)F, проведенные в точки касания , [i]перпендикулярны [/i]сторонам угла.
По [i]свойству касательных[/i] к окружности, проведенных из одной точки, отрезки касательных равны:
[red]АE[/red]=[red]АF[/red]
и образуют [i]равные углы [/i]с прямой, проходящей через вершину А и центры окружностей.
Значит
центры O_(1) и O_(2) лежат на [i]биссектрисе[/i] угла А
BC — касательная к этим окружностям, проходящая через точку К,
значит О_(1)K ⊥ BC
AK — биссектриса и высота треугольника АВС, значит Δ АВС — равнобедренный и [b]АВ=АС[/b].
и AK — медиана Δ АВС ⇒ BK=CK
Прямоугольные треугольники
Δ AEO_(1)
Δ APO_(2) по двум углам
( ∠ EAO_(2)- общий)
⇒ [b]∠ АО_(1)E= ∠ AO_(2)P [/b]
O_(1)EPO_(2) — прямоугольная трапеция.
O_(1)E=r
O_(2)E=2r
Δ AEO_(1)= Δ O_(1)MO_(2) ⇒ [b] AO_(1)[/b]=O_(1)O_(2)=[b]3r[/b]
По теореме Пифагора из треугольника АВК
R=AB*BC*AC/4S_( Δ ABC)= AB^2/2AK=3/2sqrt(21/8)=sqrt(6/7)
О т в е т. [m]sqrtfrac[/m]
📸 Видео
две окружности касаются внешним образом в точке КСкачать

Геометрия Две окружности касаются внутренним образом в точке A, причем меньшая окружность проходитСкачать

ОГЭ. Понятный разбор задачи №26. Две окружности радиусов 44 и 77 касаются внешним образом...Скачать

ОГЭ по математике. Задача 26Скачать

Две окружности разных радиусов касаются внешним образом в точке КСкачать

ЕГЭ задание 16Скачать

ОГЭ Задание 26 Внешнее касание двух окружностейСкачать

Две окружности касаются внешним образом. ЕГЭ Задача 16Скачать

Задание 26 Две окружности, внешнее касаниеСкачать

Окружности касаются внешним образом #егэ2023 #математика #егэ #школа #shorts #fypСкачать

Г: Две окружности касаются друг друга внешним образом в точке С. Радиусы окружностей равны 2 и 7Скачать

Геометрия Окружности радиусов 25 и 100 касаются внешним образом. Точки A и B лежат на первой окружСкачать

ОГЭ № 25. "Окружности касаются внешним образом... "Скачать

ОГЭ задание 26Скачать

Геометрия Две окружности радиусом R = 3 см и r = 1 см касаются внешним образом. Найти расстояние отСкачать

Геометрия Окружность радиуса 4 касается внешним образом второй окружности в точке B. ОбщаяСкачать

Задача. Две окружности касаются внутренним образом.Скачать

Три окружности касаются прямой и друг друга внешним образомСкачать