Метод вращения матрицы собственные векторы

Видео:Собственные значения и собственные векторы матрицы (4)Скачать

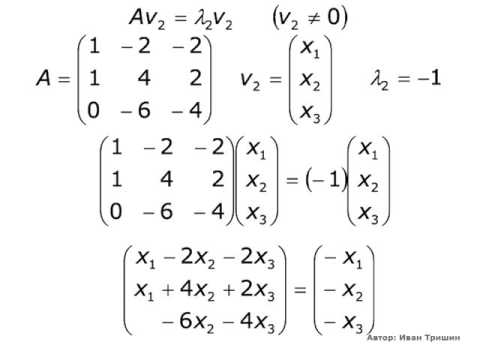
Метод вращений (метод Якоби)

Для симметричной матрицы А при отыскании собственных значений и собственных векторов в настоящее время наиболее употребительным является метод вращений (метод Якоби). При его обосновании исходят из того, что определение собственных значений и собственных векторов симметричной матрицы А равносильно построению диагональной матрицы Л и ортогональной матрицы Т, связанных соотношением (см. разд. 8.9)

Диагональные элементы матрицы Л будут искомыми собственными значениями, а столбцы матрицы Т — столбцами координат собственных векторов, соответствующих этим собственным значениям. При приближенном вычислении матриц Ли Т строят последовательность матриц

где Tij — матрицы простых вращений. Матрица Д. равна произведению всех матриц Т^, примененных при построении матриц Ло, А, А2, . Ak, причем матрицы в этом произведении перемножаются слева направо в том порядке, в каком они применялись. На к-м шаге принимают Л

Матрицу в формуле (11.2) строят следующим образом. В матрице Ak выбирают наибольший по модулю недиагональный элемент

и строят матрицу простого вращения выбирая угол +1 ^ матрицы Ak+i будет иметь вид:

Из равенства нулю этого выражения получаем

Чтобы записать матриц>’’ Tjj, нужно знать cos Пример 11.1. Методом вращений найти собственные значения и собственные векторы матрицы

Р е ш е н и е. Положим Ао = А и будем строить при к = 0 но формулам (11.2) матрицы А и Т. Так как max |а^| = |«23 I = 4, то г = 2, 3 = 3 и

Угол f определяем по формуле (11.4):

Бесконечное значение тангенса указывает на то, что угол равен — Следовательно, ср — Отсюда находим cos = 1//2, — siny> = —1/л/2 и

По первой формуле (11.2) вычисляем матрицу

Следовательно, Т = То Т23 = Т23.

По тем же формулам (11.2) при к = 1 строим матрицы А2 и Т?. Для элементов матрицы А имеем: max |а-^| = | = 4//2. Поэтому

(поскольку а[g (а^ — ^ (17 — 10) -1 = ТЛТ , которое определяется ортогональной трансформирующей матрицей. ?

Метод Якоби применяют в случае произвольной действительной, а также в случае комплексной матрицы (см. [14, 29]). Если А — комплексная матрица, то вместо матрицы (11.3) простого вращения применяют унитарную матрицу

Напомним, что по формуле Эйлера

Для эрмитовой матрицы А метод Якоби остается таким же, как и в случае действительной симметричной матрицы, а именно, для максимального уменьшения на к-м шаге (см. [14]) суммы квадратов модулей недиагональных элементов матрицы /Ц номера г и j выбирают так, чтобы элемент был наибольшим по модулю недиагональным элементом матрицы Ak, а углы ф и р находят из соотношений

Возможны и различные модификации этого метода. Например, применяют метод Якоби с циклическим перебором недиагональных элементов (см. [29]).

Пример 11.2. Методом Якоби найти собственные значения и собственные векторы эрмитовой матрицы

Решение. Положим Aq = А и построим матрицы и А. Для этого замечаем, что тах|а^| = |а.121- Поэтому принимаем i — 1, j — 2. Поскольку

то гр = argai2 = — тг/2. Далее находим

Видео:Собственные векторы и собственные значения матрицыСкачать

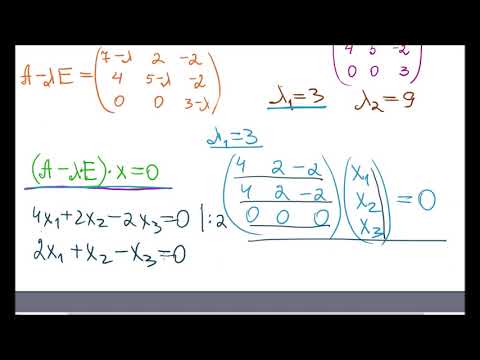
Методы решения задач о собственных
значениях и векторах матриц

Видео:Собственные векторы и собственные числа линейного оператораСкачать

Постановка задачи

Пусть [math]A[/math] — действительная числовая квадратная матрица размера [math](ntimes n)[/math] . Ненулевой вектор [math]X= bigl(x_1,ldots,x_nbigr)^T[/math] размера [math](ntimes1)[/math] , удовлетворяющий условию

называется собственным вектором матрицы [math]A[/math] . Число [math]lambda[/math] в равенстве (2.1) называется собственным значением. Говорят, что собственный вектор [math]X[/math] соответствует (принадлежит) собственному значению [math]lambda[/math] .

Равенство (2.1) равносильно однородной относительно [math]X[/math] системе:

Система (2.2) имеет ненулевое решение для вектора [math]X[/math] (при известном [math]lambda[/math] ) при условии [math]|A-lambda E|=0[/math] . Это равенство есть характеристическое уравнение:

где [math]P_n(lambda)[/math] — характеристический многочлен n-й степени. Корни [math]lambda_1, lambda_2,ldots,lambda_n[/math] характеристического уравнения (2.3) являются собственными (характеристическими) значениями матрицы [math]A[/math] , а соответствующие каждому собственному значению [math]lambda_i,

i=1,ldots,n[/math] , ненулевые векторы [math]X^i[/math] , удовлетворяющие системе

являются собственными векторами.

Требуется найти собственные значения и собственные векторы заданной матрицы. Поставленная задача часто именуется второй задачей линейной алгебры.

Проблема собственных значений (частот) возникает при анализе поведения мостов, зданий, летательных аппаратов и других конструкций, характеризующихся малыми смещениями от положения равновесия, а также при анализе устойчивости численных схем. Характеристическое уравнение вместе с его собственными значениями и собственными векторами является основным в теории механических или электрических колебаний на макроскопическом или микроскопическом
уровнях.

Различают полную и частичную проблему собственных значений, когда необходимо найти весь спектр (все собственные значения) и собственные векторы либо часть спектра, например: [math]rho(A)= max_|lambda_i(A)|[/math] и [math]min_|lambda_i(A)|[/math] . Величина [math]rho(A)[/math] называется спектральным радиусом .

1. Если для собственного значения [math]lambda_i[/math] — найден собственный вектор [math]X^i[/math] , то вектор [math]mu X^i[/math] , где [math]mu[/math] — произвольное число, также является собственным вектором, соответствующим этому же собственному значению [math]lambda_i[/math] .

2. Попарно различным собственным значениям соответствуют линейно независимые собственные векторы; k-кратному корню характеристического уравнения соответствует не более [math]k[/math] линейно независимых собственных векторов.

3. Симметрическая матрица имеет полный спектр [math]lambda_i,

i=overline[/math] , действительных собственных значений; k-кратному корню характеристического уравнения симметрической матрицы соответствует ровно [math]k[/math] линейно независимых собственных векторов.

4. Положительно определенная симметрическая матрица имеет полный спектр действительных положительных собственных значений.

Видео:Диагональный вид матрицы. Приведение матрицы к диагональному виду. Собственные векторыСкачать

Метод непосредственного развертывания

Полную проблему собственных значений для матриц невысокого порядка [math](nleqslant10)[/math] можно решить методом непосредственного развертывания. В этом случае будем иметь

Уравнение [math]P_n(lambda)=0[/math] является нелинейным (методы его решения изложены в следующем разделе). Его решение дает [math]n[/math] , вообще говоря, комплексных собственных значений [math]lambda_1,lambda_2,ldots,lambda_n[/math] , при которых [math]P_n(lambda_i)=0

(i=overline)[/math] . Для каждого [math]lambda_i[/math] может быть найдено решение однородной системы [math](A-lambda_iE)X^i=0,

i=overline[/math] . Эти решения [math]X^i[/math] , определенные с точностью до произвольной константы, образуют систему [math]n[/math] , вообще говоря, различных векторов n-мерного пространства. В некоторых задачах несколько этих векторов (или все) могут совпадать.

Видео:А.7.40 Метод Якоби поиска собственных векторов и значений симметричных матрицСкачать

Алгоритм метода непосредственного развертывания

1. Для заданной матрицы [math]A[/math] составить характеристическое уравнение (2.5): [math]|A-lambda E|=0[/math] . Для развертывания детерминанта [math]|A-lambda E|[/math] можно использовать различные методы, например метод Крылова, метод Данилевского или другие методы.

2. Решить характеристическое уравнение и найти собственные значения [math]lambda_1, lambda_2, ldots,lambda_n[/math] . Для этого можно применить методы, изложенные далее.

3. Для каждого собственного значения составить систему (2.4):

и найти собственные векторы [math]X^i[/math] .

Замечание. Каждому собственному значению соответствует один или несколько векторов. Поскольку определитель [math]|A-lambda_iE|[/math] системы равен нулю, то ранг матрицы системы меньше числа неизвестных: [math]operatorname(A-lambda_iE)=r и в системе имеется ровно [math]r[/math] независимых уравнений, а [math](n-r)[/math] уравнений являются зависимыми. Для нахождения решения системы следует выбрать [math]r[/math] уравнений с [math]r[/math] неизвестными так, чтобы определитель составленной системы был отличен от нуля. Остальные [math](n-r)[/math] неизвестных следует перенести в правую часть и считать параметрами. Придавая параметрам различные значения, можно получить различные решения системы. Для простоты, как правило, попеременно полагают значение одного параметра равным 1, а остальные равными 0.

Пример 2.1. Найти собственные значения и собственные векторы матрицы [math]Ain mathbb^[/math] , где [math]A=begin3&-2\-4&1end[/math] .

1. Запишем уравнение (2.5): [math]|A-lambda E|= begin3-lambda&-2\-4& 1-lambda end= lambda^2-4 lambda-5=0[/math] , отсюда получаем характеристическое уравнение [math]P_2(lambda)equiv lambda^2-4 lambda-5=0[/math] .

2. Находим его корни (собственные значения): [math]lambda_1=5,

3. Составим систему [math](A-lambda_iE)X^i=0,

i=1,2[/math] , для каждого собственного
значения и найдем собственные векторы:

Отсюда [math]x_1^1=-x_2^1[/math] . Если [math]x_2^1=mu[/math] , то [math]x_1^1=-mu[/math] . В результате получаем [math]X^1= bigl^T= bigl^T[/math] .

Для [math]lambda_2=-1[/math] имеем

Отсюда [math]x_2^2=2x_1^2[/math] . Если [math]x_1^2=mu[/math] , то [math]x_2^2=2mu[/math] . В результате получаем [math]X^2= bigl^T= bigl^T[/math] , где [math]mu[/math] — произвольное действительное число.

Пример 2.2. Найти собственные значения и собственные векторы матрицы [math]A= begin2&-1&1\-1&2&-1\0&0&1end[/math] .

1. Запишем характеристическое уравнение (2.5):

2. Корни характеристического уравнения: [math]lambda_=1[/math] (кратный корень), [math]lambda_3=3[/math] — собственные значения матрицы.

3. Найдем собственные векторы.

Для [math]lambda_=1[/math] запишем систему [math](A-lambda_E)cdot X^=0colon[/math]

Поскольку [math]operatorname(A-lambda_E)=1[/math] , в системе имеется одно независимое уравнение

x_3^=3[/math] , получаем [math]x_1^=1[/math] и собственный вектор [math]X^1= begin1&1&0end^T[/math] .

x_3^=1[/math] , получаем [math]x_1^=-1[/math] и другой собственный вектор [math]X^2= begin-1&0&1end^T[/math] . Заметим, что оба собственных вектора линейно независимы.

Для собственного значения [math]lambda_3=3[/math] запишем систему [math](A-lambda_3E)cdot X^3=0colon[/math]

Поскольку [math]operatorname(A-lambda_3E)=2[/math] , то выбираем два уравнения:

x_1^3=-x_2^3[/math] . Полагая [math]x_2^3=1[/math] , получаем [math]x_1^3=-1[/math] и собственный вектор [math]X^3=begin-1&1&0 end^T[/math] .

Видео:Матрицы и векторыСкачать

Метод итераций для нахождения собственных значений и векторов

Для решения частичной проблемы собственных значений и собственных векторов в практических расчетах часто используется метод итераций (степенной метод). На его основе можно определить приближенно собственные значения матрицы [math]A[/math] и спектральный радиус [math]rho(A)= max_bigl|lambda_i(A)bigr|[/math] .

Пусть матрица [math]A[/math] имеет [math]n[/math] линейно независимых собственных векторов [math]X^i,

i=1,ldots,n[/math] , и собственные значения матрицы [math]A[/math] таковы, что

Видео:А.7.35 Собственные вектора и собственные значения матрицыСкачать

Алгоритм метода итераций

1. Выбрать произвольное начальное (нулевое) приближение собственного вектора [math]X^[/math] (второй индекс в скобках здесь и ниже указывает номер приближения, а первый индекс без скобок соответствует номеру собственного значения). Положить [math]k=0[/math] .

lambda_1^= frac<x_i^><x_i^>[/math] , где [math]i[/math] — любой номер [math]1leqslant ileqslant n[/math] , и положить [math]k=1[/math] .

4. Найти [math]lambda_1^= frac<x_i^><x_i^>[/math] , где [math]x_i^, x_i^[/math] — соответствующие координаты векторов [math]X^[/math] и [math]X^[/math] . При этом может быть использована любая координата с номером [math]i,

1leqslant ileqslant n[/math] .

5. Если [math]Delta= bigl|lambda_1^- lambda_1^bigr|leqslant varepsilon[/math] , процесс завершить и положить [math]lambda_1cong lambda_1^[/math] . Если varepsilon»>[math]Delta>varepsilon[/math] , положить [math]k=k+1[/math] и перейти к пункту 3.

1. Процесс последовательных приближений

сходится, т.е. при [math]xtoinfty[/math] вектор [math]X^[/math] стремится к собственному вектору [math]X^1[/math] . Действительно, разложим [math]X^[/math] по всем собственным векторам: [math]textstyle<X^= sumlimits_^ c_iX^i>[/math] . Так как, согласно (2.4), [math]AX^i= lambda_iX^i[/math] , то

При большом [math]k[/math] дроби [math]<left(fracright)!>^k, ldots, <left(fracright)!>^k[/math] малы и поэтому [math]A^kX^= c_1lambda_1^kX^1[/math] , то есть [math]X^to X^1[/math] при [math]ktoinfty[/math] . Одновременно [math]lambda_1= limlimits_ frac<x_^><x_^>[/math] .

2. Вместо применяемой в пункте 4 алгоритма формулы для [math]lambda_1^[/math] можно взять среднее арифметическое соответствующих отношений для разных координат.

3. Метод может использоваться и в случае, если наибольшее по модулю собственное значение матрицы [math]A[/math] является кратным, т.е.

4. При неудачном выборе начального приближения [math]X^[/math] предел отношения [math]frac<x_i^><x_i^>[/math] может не существовать. В этом случае следует задать другое начальное приближение.

5. Рассмотренный итерационный процесс для [math]lambda_1[/math] сходится линейно, с параметром [math]c=frac[/math] и может быть очень медленным. Для его ускорения используется алгоритм Эйткена.

6. Если [math]A=A^T[/math] (матрица [math]A[/math] симметрическая), то сходимость процесса при определении [math]rho(A)[/math] может быть ускорена.

7. Используя [math]lambda_1[/math] , можно определить следующее значение [math]lambda_2[/math] по формуле [math]lambda_2= frac<x_i^- lambda_1 x_i^><x_i^- lambda_1 x_i^>

(i=1,2,ldots,n)[/math] . Эта формула дает грубые значения для [math]lambda_2[/math] , так как значение [math]lambda_1[/math] является приближенным. Если модули всех собственных значений различны, то на основе последней формулы можно вычислять и остальные [math]lambda_j

8. После проведения нескольких итераций рекомендуется «гасить» растущие компоненты получающегося собственного вектора. Это осуществляется нормировкой вектора, например, по формуле [math]frac<X^><|X^|_1>[/math] .

Пример 2.3. Для матрицы [math]A=begin5&1&2\ 1&4&1\ 2&1&3 end[/math] найти спектральный радиус степенным методом с точностью [math]varepsilon=0,,1[/math] .

1. Выбирается начальное приближение собственного вектора [math]X^= begin 1&1&1 end^T[/math] . Положим [math]k=0[/math] .

5. Так как varepsilon»>[math]bigl|lambda_1^- lambda_1^bigr|= 0,!75> varepsilon[/math] , то процесс необходимо продолжить. Результаты вычислений удобно представить в виде табл. 10.10.

Точность по достигнута на четвертой итерации. Таким образом, в качестве приближенного значения [math]lambda_1[/math] берется 6,9559, а в качестве собственного вектора принимается [math]X^1= begin 2838& 1682& 1888end^T[/math] .

Так как собственный вектор определяется с точностью до постоянного множителя, то [math]X^1[/math] лучше пронормировать, т.е. поделить все его компоненты на величину нормы. Для рассматриваемого примера получим

Согласно замечаниям, в качестве собственного значения [math]lambda_1[/math] матрицы можно взять не только отношение

а также их среднее арифметическое [math]fracapprox 6,!8581[/math] .

Пример 2.4. Найти максимальное по модулю собственное значение матрицы [math]A=begin2&-1&1\ -1&2&-1\ 0&0&3 end[/math] и соответствующий собственный вектор.

1. Зададим начальное приближение [math]X^= begin1&-1&1 end^T[/math] и [math]varepsilon=0,!0001[/math] .

Выполним расчеты согласно методике (табл. 10.11).

В результате получено собственное значение [math]lambda_1cong 3,!00003[/math] и собственный вектор [math]X^1= begin 88573&-88573&1end^T[/math] или после нормировки

Видео:Собственные значения и собственные векторыСкачать

Метод вращений для нахождения собственных значений

Метод используется для решения полной проблемы собственных значений симметрической матрицы и основан на преобразовании подобия исходной матрицы [math]Ainmathbb^[/math] с помощью ортогональной матрицы [math]H[/math] .

Напомним, что две матрицы [math]A[/math] и [math]A^[/math] называются подобными ( [math]Asim A^[/math] или [math]A^sim A[/math] ), если [math]A^=H^AH[/math] или [math]A=HA^H^[/math] , где [math]H[/math] — невырожденная матрица.

В методе вращений в качестве [math]H[/math] берется ортогональная матрица, такая, что [math]HH^=H^H=E[/math] , т.е. [math]H^=H^[/math] . В силу свойства ортогонального преобразования евклидова норма исходной матрицы [math]A[/math] не меняется. Для преобразованной матрицы [math]A^[/math] сохраняется ее след и собственные значения [math]lambda_icolon[/math]

[math]operatorname

A= sum_^a_= sum_^ lambda_i(A)= operatorname

A^.[/math]

При реализации метода вращений преобразование подобия применяется к исходной матрице [math]A[/math] многократно:

Формула (2.6) определяет итерационный процесс, где начальное приближение [math]A^=A[/math] . На k-й итерации для некоторого выбираемого при решении задачи недиагонального элемента [math]a_^,

ine j[/math] , определяется ортогональная матрица [math]H^[/math] , приводящая этот элемент [math]a_^[/math] (а также и [math]a_^[/math] ) к нулю. При этом на каждой итерации в качестве [math]a_^[/math] выбирается наибольший по модулю. Матрица [math]H^[/math] называемая матрицей вращения Якоби, зависит от угла [math]varphi^[/math] и имеет вид

В данной ортогональной матрице элементы на главной диагонали единичные, кроме [math]h_^= cosvarphi^[/math] и [math]h_^=cosvarphi^[/math] , а остальные элементы нулевые, за исключением [math]h_^=-sinvarphi^[/math] , [math]h_^=sinvarphi^[/math] ( [math]h_[/math] -элементы матрицы [math]H[/math] ).

Угол поворота [math]varphi^[/math] определяется по формуле

где [math]|2varphi^|leqslant frac,

i ( [math]a_[/math] выбирается в верхней треугольной наддиагональной части матрицы [math]A[/math] ).

В процессе итераций сумма квадратов всех недиагональных элементов [math]sigms(A^)[/math] при возрастании [math]k[/math] уменьшается, так что [math]sigms(A^) . Однако элементы [math]a_^[/math] приведенные к нулю на k-й итерации, на последующей итерации немного возрастают. При [math]ktoinfty[/math] получается монотонно убывающая ограниченная снизу нулем последовательность sigma(A^)> ldots> sigma(A^)>ldots»>[math]sigma(A^)> sigma(A^)> ldots> sigma(A^)>ldots[/math] . Поэтому [math]sigma(A^)to0[/math] при [math]ktoinfty[/math] . Это и означает сходимость метода. При этом [math]A^to Lambda= operatorname(lambda_1,ldots,lambda_n)[/math] .

Замечание. В двумерном пространстве с введенной в нем системой координат [math]Oxy[/math] с ортонормированным базисом [math]<vec,vec>[/math] матрица вращения легко получается из рис. 2.1, где система координат [math]Ox’y'[/math] повернута на угол [math]varphicolon[/math]

Таким образом, для компонент [math]vec,’,, vec,'[/math] будем иметь [math]bigl(vec,’,vec,’bigr)= bigl(vec,vecbigr)cdot! begin cos varphi&-sin varphi\ sin varphi& cos varphiend[/math] . Отсюда следует, что в двумерном пространстве матрица вращения имеет вид [math]H= begin cos varphi&-sin varphi\ sin varphi& cos varphiend[/math] . Отметим, что при [math]n=2[/math] для решения задачи требуется одна итерация.

Видео:7 4 Собственные векторы и собственные значенияСкачать

Алгоритм метода вращений

1. Положить [math]k=0,

A^=A[/math] и задать 0″>[math]varepsilon>0[/math] .

2. Выделить в верхней треугольной наддиагональной части матрицы [math]A^[/math] максимальный по модулю элемент [math]a_^,

Если [math]|a_^|leqslant varepsilon[/math] для всех [math]ine j[/math] , процесс завершить. Собственные значения определяются по формуле [math]lambda_i(A^)=a_^,

Собственные векторы [math]X^i[/math] находятся как i-e столбцы матрицы, получающейся в результате перемножения:

Если varepsilon»>[math]bigl|a_^bigr|>varepsilon[/math] , процесс продолжается.

3. Найти угол поворота по формуле [math]varphi^= frac operatorname frac<2a_^><a_^-a_^>[/math] .

4. Составить матрицу вращения [math]H^[/math] .

5. Вычислить очередное приближение [math]A^= bigl(H^bigr)^T A^ H^[/math] .Положить [math]k=k+1[/math] и перейти к пункту 2.

1. Используя обозначение [math]overline

_k= frac<2a_^><a_^-a_^>[/math] , можно в пункте 3 алгоритма вычислять элементы матрицы вращения по формулам

2. Контроль правильности выполнения действий по каждому повороту осуществляется путем проверки сохранения следа преобразуемой матрицы.

3. При [math]n=2[/math] для решения задачи требуется одна итерация.

Пример 2.5. Для матрицы [math]A=begin 2&1\1&3 end[/math] методом вращений найти собственные значения и собственные векторы.

1. Положим [math]k=0,

2°. Выше главной диагонали имеется только один элемент [math]a_=a_=1[/math] .

3°. Находим угол поворота матрицы по формуле (2.7), используя в расчетах 11 цифр после запятой в соответствии с заданной точностью:

4°. Сформируем матрицу вращения:

5°. Выполним первую итерацию:

Очевидно, след матрицы с заданной точностью сохраняется, т.е. [math]sum_^a_^= sum_^a_^=5[/math] . Положим [math]k=1[/math] и перейдем к пункту 2.

2. Максимальный по модулю наддиагональный элемент [math]|a_|= 4,!04620781325cdot10^ . Для решения задачи (подчеркнем, что [math]n=2[/math] ) с принятой точностью потребовалась одна итерация, полученную матрицу можно считать диагональной. Найдены следующие собственные значения и собственные векторы:

Пример 2.6. Найти собственные значения и собственные векторы матрицы [math]A=begin5&1&2\ 1&4&1\ 2&1&3 end[/math] .

1. Положим [math]k=0,

2°. Выделим максимальный по модулю элемент в наддиагональнои части: [math]a_^=2[/math] . Так как varepsilon=0,!001″>[math]a_=2> varepsilon=0,!001[/math] , то процесс продолжается.

3°. Находим угол поворота:

4°. Сформируем матрицу вращения: [math]H^= begin0,!85065&0&-0,!52573\ 0&1&0\ 0,!52573&0&0,!85065 end[/math] .

5°. Выполним первую итерацию: [math]A^= bigl(H^bigr)^T A^H^= begin 6,!236&1,!376&2,!33cdot10^\ 1,!376&4&0,!325\ 2,!33cdot10^&0,!325&1,!764 end[/math] . Положим [math]k=1[/math] и перейдем к пункту 2.

2(1). Максимальный по модулю наддиагональный элемент [math]a_^=1,!376[/math] . Так как varepsilon=0,!001″>[math]a_^> varepsilon=0,!001[/math] , процесс продолжается.

3(1). Найдем угол поворота:

4(1). Сформируем матрицу вращения: [math]H^= begin 0,!902937&-0,!429770&0\ 0,!429770&0,!902937&0\ 0&0&1 end[/math] .

5(1). Выполним вторую итерацию: [math]A^= bigl(H^bigr)^T A^H^= begin 6,!891& 2,!238cdot10^&0,!14\ 2,!238cdot10^& 3,!345&0,!293\ 0,!14&0,!293&1,!764 end[/math] . Положим [math]k=2[/math] и перейдем к пункту 2.

2(2). Максимальный по модулю наддиагональный элемент varepsilon=0,!001″>[math]a_^=0,!293> varepsilon=0,!001[/math] .

3(2). Найдем угол поворота:

4(2). Сформируем матрицу вращения [math]H^= begin1&0&0\ 0&0,!9842924& -0,!1765460\ 0& 0,!1765460& 0,!9842924end[/math] .

5(2). Выполним третью итерацию и положим [math]k=3[/math] и перейдем к пункту 2:

2(3). Максимальный по модулю наддиагональный элемент varepsilon»>[math]a_^= 0,!138>varepsilon[/math] .

3(3). Найдем угол поворота:

4(3). Сформируем матрицу вращения: [math]H^= begin 0,!999646&0&-0,!026611\ 0&1&0\ 0,!026611&0&0,!999646 end[/math] .

5(3). Выполним четвертую итерацию и положим [math]k=4[/math] и перейдем к пункту 2:

2(4). Так как varepsilon»>[math]a_^=0,!025>varepsilon[/math] , процесс повторяется

3(4). Найдем угол поворота

4(4). Сформируем матрицу вращения: [math]H^= begin 0,!9999744&-0,!0071483&0\ 0,!0071483&0,!9999744&0\ 0&0&1 end[/math] .

5(4). Выполним пятую итерацию и положим [math]k=5[/math] и перейдем к пункту 2:

2(5). Так как наибольший по модулю наддиагональный элемент удовлетворяет условию [math]bigl|-6,!649cdot10^bigr| , процесс завершается.

Собственные значения: [math]lambda_1cong a_^= 6,!895,,

lambda_3cong a_^=1,!707,,[/math] . Для нахождения собственных векторов вычислим

X^3=begin-0,!473\-0,!171\0,!864 end[/math] или после нормировки

Видео:Собственные векторы и собственные числа линейного оператораСкачать

Метод вращений

Одним из эффективных методов, позволяющих привести исходную симметрическую матрицу n-го порядка к трехдиагональному виду, является метод вращений. Он основан на специально подбираемом вращении системы координат в n-мерном пространстве. Поскольку любое вращение можно заменить последовательностью элементарных (плоских) вращений, то решение задачи можно разбить на ряд шагов, на каждом из которых осуществляется плоское вращение. Таким образом, на каждом шаге выбираются две оси – i-я и j-я (i≠ j),и поворот на угол φ производится в плоскости, проходящей через эти оси; остальные оси координат на данном шаге неподвижны. Матрица вращения при этом имеет вид

(3.8)

Здесь мы рассматриваем матрицы с вещественными элементами. В случае комплексных векторов для использования этого метода нужно изменить формулы (3.8).

Для осуществления преобразования подобия (3.7) необходимо найти обратную матрицу . Можно показать, что она равна в рассматриваемом случае транспонированной матрице . Для получения обратной матрицы достаточно провести зеркальное отражение всех элементов исходной матрицы относительно ее диагонали. Другими словами, нужно поменять местами строки и столбцы исходной матрицы; элементы pijи pjiпри этом поменяются местами.

Угол поворота φ на каждом шаге выбирают таким, чтобы в преобразованной матрице обратился в нуль один элемент (в симметрической матрице – два). Процесс преобразования исходной матрицы путем элементарного вращения на любом k—мшаге можно представить в виде рекуррентных соотношений:

(3.9)

Здесь матрицы вращений Р и значения i,jзависят от номера шага k.

Рассмотрим первый шаг преобразования. Сначала вычисляют произведение матриц (здесь А(0) – исходная матрица А).Как видно из (3.8), в полученной матрице отличными от исходных являются элементы, стоящие в i-м и j—мстолбцах; остальные элементы совпадают с элементами матрицы A(0) т.е.

(3.10)

Затем находят преобразованную матрицу . Элементы полученной матрицы отличаются от элементов матрицы В только i-й и j—йстроками. Они связаны соотношениями:

(3.11)

Таким образом, преобразованная матрица отличается от элементами строк и столбцов с номерами iи j. Эти элементы пересчитывают по формулам (3.10), (3.11). В данных формулах пока не определенными остались параметры р и q; при этом лишь один из них свободный, поскольку они подчиняются тождеству:

(3.12)

Недостающее одно уравнение для определения этих параметров получают из условия обращения в нуль некоторого элемента новой матрицы А(1)В зависимости от выбора этого элемента строят различные алгоритмы метода вращений.

Одним из таких алгоритмов является последовательное обращение в нуль всех ненулевых элементов, лежащих вне трех диагоналей исходной симметрической матрицы. Это так называемый прямой метод вращений. В соответствии с этим методом обращение в нуль элементов матрицы осуществляют последовательно, начиная с элементов первой строки (и первого столбца, так как матрица симметрическая).

Процесс вычислений поясним с использованием схематического изображения матрицы (рис. 3.1). Точками отмечены элементы матрицы. Наклонные линии указывают три диагонали матрицы, элементы на которых после окончания расчета отличны от нуля. Алгоритм решения задачи нужно построить таким образом, чтобы все элементы по одну сторону от этих трех диагоналей обратились в нуль; тогда симметрично расположенные элементы также станут нулевыми. Обращение элементов в нуль можно выполнять, например, в следующей последовательности: a13, a14, … , a1n, a24, a25, …, a2n, …, an-2, n.

Рассмотрим сначала первый шаг данного метода, состоящий в обращении в нуль элемента а13 (и автоматически a31). Для осуществления элементарного вращения нужно выбрать две оси — i-ю и j—ю,так чтобы элемент а13 оказался в строке или столбце с номером i или j. Положим i = 2, j= 3 и умножим матрицу А(0)справа на матрицу вращения Р23 и слева на транспонированную матрицу Р23T. Получим новые значения элементов матрицы, которые вычисляем по формулам (3.10), (3.11). Полагая в них l=1 и т = 3, находим

Учитывая тождество (3.12), получаем систему уравнений для определения параметров р, q:

Рис. 3.1. Схематическое изображение матрицы к иллюстрации метода вращений

Решая эту систему, находим

Используя эти параметры р, q, можно по формулам (3.10), (3.11) вычислить значения элементов, стоящих в строках и столбцах с номерами i — 2, 3; j — 2, 3(остальные элементы исходной матрицы не изменились).

Аналогично, выбирая для элементарного вращения i-ю и j-ю оси, можно добиться нулевого значения любого элемента на k—мшаге. В этом случае строят матрицу вращения Рij, параметры которой вычисляют по формулам, полученным из условия равенства нулю элемента и (3.12). Эти формулы имеют вид

С учетом найденных значений параметров р, qможно по формулам (3.10), (3.11) найти элементы преобразованной матрицы. Для иллюстрации вновь обратимся к рис. 3.1. Вертикальными линиями показаны столбцы с номерами iи j, соответствующими осям элементарного вращения, горизонтальными – строки с теми же номерами. На рассматриваемом шаге матрица преобразуется таким образом, чтобы отмеченные крестиками элементы обратились в нуль. Элементарное вращение (3.9) на каждом шаге требует пересчета всех элементов отмеченных столбцов и строк. С учетом симметрии можно вычислить лишь все элементы столбцов, а элементы получаются из условий симметрии. Исключение составляют лишь элементы, расположенные на пересечениях этих строк и столбцов. Они изменяются на каждом из двух этапов выполняемого шага.

Таким образом, на каждом шаге преобразования симметрической матрицы для вычисления элементов столбцов используют формулы (3.10), а элементы, находящиеся на пересечениях изменяемых строк и столбцов, пересчитывают еще по формулам (3.11). При этом полученные ранее нулевые элементы не изменяются. Алгоритм приведения симметрической матрицы к трехдиагональному виду с помощью прямого метода вращений представлен на рис. 3.2.

Рис. 3.2. Алгоритм приведения симметрической матрицы к трехдиагональному виду с помощью прямого метода вращений

Собственные значения полученной трехдиагональной матрицы будут также собственными значениями исходной матрицы. Собственные векторы xi исходной матрицы не равны непосредственно собственным векторам yiтрехдиагональной матрицы, а вычисляют их с помощью соотношений

🔍 Видео

Вычислительные методы алгебры - Степенной метод, метод вращенийСкачать

Трехмерные линейные трансформации | Сущность Линейной Алгебры, примечаниеСкачать

Собственные векторы и собственные значенияСкачать

Математика без Ху!ни. Метод Гаусса. Совместность системы. Ранг матрицы.Скачать

Матрица переходаСкачать

Собственные значения и собственные векторы. ТемаСкачать

Айгенвектора и айгензначения | Сущность Линейной Алгебры, глава 10Скачать

Собственные значения и собственные векторы. ПримерСкачать

Матрица поворотаСкачать

Собственные значения матрицыСкачать