Вы уже наверняка не раз сталкивались с такими понятиями как векторы и матрицы. Вектор – это обыкновенный столбец с числами. Матрица представляет собой сборный блок с объектами. Именно на работе с этими элементами построен принцип функционирования программы Excel. В этом уроке мы расскажем о том, как работать с такими вычислениями в программе Маткад и акцентируем внимание на том, почему процесс работы в данном ПО куда проще и удобнее.
Мы уже рассказывали в своих уроках о том, что все наши векторы начинались с элемента с нулевым значением. Сейчас же мы поставим номером первого элемента цифру один, ведь так нам гораздо проще будет сориентироваться в учебном материале.
Данное значение можно внести прямо в рабочее поле.
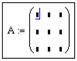
Посмотрите на матрицы на рисунке ниже.
Как вы можете заметить, в них входят и числа, и функции. Помимо этого, сюда можно внести и текст. Чтобы вывести элемент матрицы, воспользуйтесь подстрочным индексом.
Матрицы, описанные на скрине повыше, относятся к квадратному типу. Тем не менее, пользователь может самостоятельно устанавливать их размерные рамки.
Примите во внимание, что первое число обозначает общую нумерацию строчки, а второе – номер столбика.
Для векторного столбца второй индекс можно удалить. Для строки же он является обязательным.
Нужные команды, для всевозможного выделения строчек или столбиков вы всегда сможете отыскать во вкладке «Математика».
Большинство операций для векторных и матричных конструкций вполне соответствуют работе со стандартными числами и функциями. Для того, чтобы отыскать обратную матрицу, потребуется действовать по аналогии с операциями деления. Пользователь может записать операторы, задав им наименования матриц и векторов. Например, это может выглядеть так:
Более подробно мы рассмотрим данный опционал немного погодя. Стоит отметить, что такая функция нуждается в девяти операциях умножения и в таком же количестве деления. Согласитесь, что расписывать все эти процессы достаточно скучно. К тому же, с большими матрицами такой подход нерациональный.
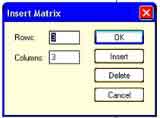
Методика применения векторов отличается значительным разнообразием. Чтобы разработать вектор или матрицу, понадобится открыть вкладку «Вставить матрицу». На экране появится сетка с изображением маленьких квадратиков.
Перемещаем указатель на эту сетку. Настраиваем курсор на нужные габариты матрицы. Кликаем дважды ЛКМ.
На экране появляется новая матрица.
Матрица может быть переименована, после того, как пользователь дважды кликнет по левой скобке.
Чтобы быстро вставить или удалить строчки да столбцы, можно вызвать контекстное меню «Операторы с векторамиматрицами» на одноименной вкладке.
Работа с матрицами
Эффекты от матриц или вектором гораздо проще сообразить, пользуясь специально разработанными символами. Обратите внимание на скрин ниже.
Оператор транспортировки вызывается посредством выполнения операции Математика –> Операторы –> Векторы и матрицы:
Кликаем по правой стороне матрицы и применяем оператор. Он подходит как для символьных, так и численных матриц.
Операции в векторах часто выполняются по одному элементу. В этой ситуации можно воспользоваться очень удобным оператором, который отвечает за разработку вектора. Чтобы перемножить два вектора, понадобится выполнить простой пример.
Теперь нам нужно выбрать нужные параметры и активировать векторизацию.
Вычисляем заданные параметры и смотрим на результат. Первый элемент приумножился на второй, и так далее.
Еще примеры таких опций.
Операции поэлементного типа могут применяться исключительно к массивам одинакового размера.
Добавление и вычитание
Данные операции относятся к поэлементному типу.
Она также применяется к массивам одинакового размерного типа.
Пользуясь оператором, предназначенным для суммирования, можно отыскать сумму всех векторных частей.
Скалярное произведение работает по представленному ниже принципу.
При таком типе умножения матриц, программа занимается умножением данных элементов по столбцам. Данная операция может применяться исключительно к тем матрицам, которые характеризуются равным количеством строчек и столбцов.
Обратите внимание, что немалая роль отводится поочередности множителей.
Только в редких случаях скалярное произведение может стать коммутативным.
Скаляр двух векторов показывает результат как на фотографии ниже.
Данная опция может использоваться исключительно для двух векторных столбов из трех элементов.
Векторное произведение часто используется для механики, гидродинамики и огромного количества подобных сфер деятельности.
Обратная матрица может быть применима для квадратных матриц:
В результате у нас получится матрица единичного типа
Если произвести матрицу и единичную матрицу, мы получим первоначальный вариант.
Определитель может быть разработан исключительно для матрицы квадратного типа. Он может быть нулевым в любых условиях. Обратная матрица имеет в своей структуре дроби, в состав которых входит определитель.
В ситуациях, когда определитель установлен на ноль, к нему нереально подобрать обратную матрицу. Сама матрица автоматически становится сингулярной. О таких изменениях пользователь узнает из оповещения программы.
В ситуациях со скалярами, определитель соответствует их модулям
Команда «определитель» помогает отыскать длину вектора .
Уважаемые пользователи, хотим Вас проинформировать о том, что некоторые антивирусные программы и браузеры ложно срабатывают на дистрибутив программы MediaGet, считая его зараженным. Данный софт не содержит никаких вредоносных программ и вирусов и многие из антивирусов просто Вас предупреждают, что это загрузчик (Downloader). Если хотите избежать подобных проблем, просто добавьте MediaGet в список доверенных программ Вашей антивирусной программы или браузера.
Выбрав нужную версию программы и кликнув ссылку, Вам на компьютер скачивается дистрибутив приложения MediaGet, который будет находиться в папке «Загрузки» для Вашего браузера. Находим этот файл с именем программы и запускаем его. И видим первый этап установки. Нажимаем унопку «Далее»
Далее Вам предлагается прочитать и одобрить лицензионное соглашение. Нажимаем кнопку «Принимаю»
В следующем окне Вам предлагается бесплатное полезное дополнительное программоное обеспечение, будь то антивирус или бразуер. Нажимаем кнопку «Принимаю». Также Вы можете отказаться от установки дополнительного ПО, нажав кнопку «Отклоняю»
Далее происходит процесс установки программы. Вам нужно выбрать папку, в которую будут скачиваться нужные Вам файлы.
Происходит завершение установки. Программа автоматически открывается и скачивает нужные Вам исходные файлы.
Обратите внимание, что предоставляемое программное обеспечение выкладывается исключительно для личного использования и ознакомления. Все файлы, доступные для скачивания, не содержат вирусов и вредоносных программ.
Видео:7. MathCad. Векторы и матрицыСкачать

Урок 21. Векторы и матрицы в Mathcad
С этими понятиями Вы могли сталкиваться, работая в Excel – столбец чисел называется вектор-столбцом, строка – вектор-строкой. Блок объектов является матрицей. Вычисления в Excel, по сути, являются операциями с векторами и матрицами. В этом уроке мы познакомимся с аналогичными вычислениями в Mathcad, и мы поймем, почему в Mathcad их проводить проще.
Введение
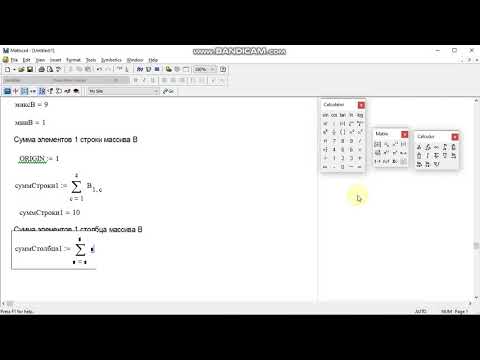
В предыдущих уроках наши векторы начинались с элемента с номером «0». В этом уроке для простоты сделаем номер первого элемента равным «1». Это можно сделать с помощью вкладки Расчет –> Параметры документа –> ORIGIN:
Это значение можно вывести прямо в документ, чтобы не забыть его и не запутаться:
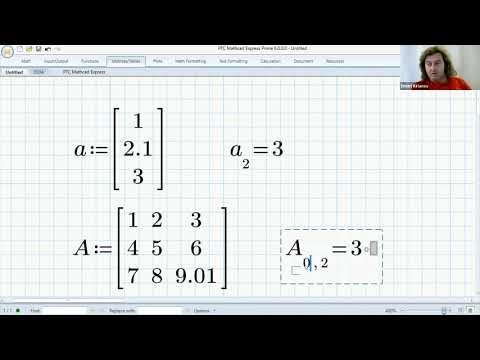
Теперь рассмотрим несколько матриц:
Как видно, они могут включать в себя числа, символы и даже функции. Они также могут содержать текстовые элементы (строки).
Элемент матрицы можно вывести, используя подстрочные индексы:
Матрицы выше являются квадратными 2х2, но у них может быть любой размер по строкам и столбцам:
Запомните: первое число – номер строки (или их количество), второе – столбца.
Элементы, выделенные с помощью подстрочных индексов:
Для вектор-столбца второй индекс можно опустить, но не для вектор-строки:
Во вкладке Математика –> Операторы и символы –> Операторы –> Векторы и матрицы Вы найдете команды для выделения столбцов и строк:
Многие операции для векторов и матриц аналогичны операциям для обычных чисел, переменных и функций: сложение, вычитание, некоторые виды умножения. Поиск обратной матрицы близко к операции деления. Вы можете записать эти операторы, используя имена векторов и матриц. В качестве примера рассмотрим векторное произведение матрицы и вектора:
Мы рассмотрим эту операцию подробнее позже. Однако стоит заметить, что она требует девять операций умножения и девять – сложения. Расписывать их утомительно и чревато ошибками – для больших матриц сделать это очень трудно.
Применение векторов очень широко. Вспомните пиксели на экране монитора – их могут быть миллионы. Они обрабатываются с помощью операций с матрицами.
В Mathcad
Для создания вектора или матрицы откройте вкладку Матрицы/таблицы. Когда курсор находится в пустой области щелкните по самой левой кнопке «Вставить матрицу». Появится сетка с маленькими квадратами:
Перемести указатель на сетку, выберите желаемый размер матрицы, затем щелкните левой кнопкой мыши. Появится пустая матрица:
Матрице можно присвоить имя, щелкнув на левую скобку, нажав [:] для оператора присваивания и введя имя:
Вставку и удаление строк и столбцов легко осуществлять с помощью команд из меню «Операторы с векторами/матрицами» на вкладке Матрицы и таблицы:
Операции с матрицами
Эффект от различных операций с матрицами и векторами будет проще понять, используя символы. Будем использовать две матрицы и два вектора:
Оператор транспонирования находится на вкладке Математика –> Операторы –> Векторы и матрицы:
Щелкните по правой границе матрицы и примените оператор. Он работает как для символьных, так и для числовых матриц:
Часто операции в векторами приходится совершать поэлементно. Для этого служит оператор векторизации. Операции в Excel зачастую являются поэлементными, они также важны и в Mathcad. Чтобы перемножить два вектора поэлементно, сначала введите простое умножение:
Затем выберите все выражение и примените векторизацию:
Вычислите, чтобы посмотреть результат: первый элемент умножается на первый, второй – на второй, и т.д.:
Другие поэлементные операции:
Поэлементные операции применимы только к массивам одного размера.
Сложение и вычитание
Сложение и вычитание выполняется поэлементно:
Эта операция также применима лишь к массивам одного размера.
С помощью оператора суммирования можно найти сумму всех элементов вектора (не матрицы):
Умножение на константу работает так:
При скалярном умножении матриц происходит умножение строк на столбцы. При этом используется тот же символ, что и при обычном умножении. Эта операция допустима только для тех матриц, в которых число строк в первой матрице равно числе столбцов во второй. Для наших матриц 2х2:
Заметьте, что последовательность множителей играет роль:
Скалярное произведение не коммутативно, за исключением особых случаев:
Скалярное произведение двух векторов дает результат с комплексно-сопряженными числами (с чертой сверху). Для действительных чисел на это можно не обращать внимания:
Этот оператор применим только для двух вектор-столбцов, состоящих из трех элементов:
Векторное произведение имеет широкое применение в механике, гидродинамике, электромагнетизме и в других областях.
Обратная матрица определяется только для квадратных матриц:
Произведение матрицы и ее обратной матрицы является единичной матрицей:
Произведение матрицы и единичной матрицы дает изначальную матрицу:
Определитель можно найти только для квадратной матрицы. Его значение может быть равно нулю, даже если все элементы матрицы не равны нулю. Обратная матрица содержит дроби, в знаменателе которых находится определитель:
Если определитель равен нулю, обратной матрицы не существует, а матрица является сингулярной. Вспомните деление на ноль в обычной алгебре. Mathcad сообщит, если матрица является сингулярной:
Для скаляра определитель равен его модулю:
Для вектора команда Определитель вычисляет длину вектора:
Резюме
В этом уроке мы рассмотрели векторы и матрицы (массивы).
- Элементы массива можно вывести с помощью подстрочного индекса – один индекс для вектор-столбца, два – для других массивов. Первое индекс – для строк, второй – для столбцов.
- Есть специальные команды для извлечения отдельных строк и столбцов.
- Векторы и матрицы создаются и редактируются с помощью команд со вкладки Матрицы/таблицы.
Операции над векторами и матрицами, которые мы рассмотрели:
- Транспонирование.
- Поэлементные операции.
- Сложение и вычитание.
- Скалярное произведение.
- Векторное произведение.
- Поиск обратной матрицы.
- Поиск определителя.
Видео:Функции для работы с матрицами и векторами в MathCAD 14 (21/34)Скачать
Маткад работа с векторами и матрицами
БАЗОВЫЕ ОПЕРАЦИИ.
РАНЖИРОВАННЫЕ ПЕРЕМЕННЫЕ. ФУНКЦИИ. ГРАФИКИ
МАССИВЫ
1 Запуск. Формульные и текстовые области
Запуск Mathcad: Start / All Programs / Mathsoft Apps / Mathcad (Пуск / Все программы / Mathsoft Apps / Mathcad).
Документ Mathcad просматривается, интерпретируется и выполняется слева направо и сверху вниз и может включать три вида областей:
Для ввода математических символов: View / Toolbars / Math (Вид / Панели инструментов / Математическая).
Каждое математическое выражение набирается в отдельной формульной области. Одна формула – одна область!
Перемещение курсора — клавиша Пробел. Изменение направления уголка — клавиша Insert (Ins).
«:=» — «присвоить» — задать выражение (число или формулу)
«=» — «вычислить» подсчитать и вывести значение выражения.
Для вставки в документ текстовой области выполняют Insert / Text Region (Вставка / Область текста), либо просто нажимают в формульной области Пробел. Текстовая область имеет рамку с маркерами, позволяющими изменять ее размеры, и курсор в виде вертикальной линии красного цвета.
2 Ранжированные переменные. Функции. Графики
В Mathcad существует тип переменных, принимающих не одно, а множество значений. Такие переменные носят название ранжированных или дискретных. Ранжированная переменная – переменная, которая принимает ряд значений при каждом ее использовании, причем каждое значение отличается от соседнего на постоянную величину, называемую шагом.
Ранжированная переменная общего вида определяется выражением:
Имя := x1, x2 .. xn
Здесь Имя – задаваемое пользователем имя ранжированной переменной;
x1 – первое значение ранжированной переменной;
x2 – второе значение ранжированной переменной (x2 = x1 + Dx — первое значение плюс шаг);
xn – последнее значение ранжированной переменной.
Значения x1 и x2 разделяются запятой, двоеточие представляет собой единый оператор, указывающий на изменение переменной в заданных пределах. Он вводится с клавиатуры клавишей «;» или выбирается с палитры математических инструментов Matrix (Векторы и матрицы) (кнопка 
Например, если переменная изменяется в интервале 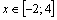
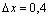
Шаг изменения значений ранжированной переменной в явном виде обычно не задается, он определяется как x2 – x1.
Функции в системе Mathcad можно условно разделить на две группы: встроенные и функции пользователя. Встроенные функции изначально заданы в системе разработчиками. Имя функции вводится с клавиатуры, обычно в нижнем регистре. Полный перечень встроенных функций можно получить, выполнив команду Function (Функция) главного меню Insert (Вставка), или нажав на кнопку 
Среди наиболее часто используемых функций можно указать:
- sin(z) — синус z (z задается в радианах);
- cos(z) — косинус z;
- tan(z) — тангенс z;
- cot(z) — котангенс z;
- exp(z) – экспоненциальная функция, значение е (основание натурального логарифма) в степени z;
- ln(z) – натуральный логарифм z;
- log(z) – десятичный логарифм числа z;
- log(z, b) – логарифм числа z по основанию b;
- acos(z) – арккосинус z;
- acot(z) – арккотангенс z;
- asin(z) – арксинус z;
- atan(z) – арктангенс z.
Функция пользователя сначала должна быть определена, а затем к ней можно обращаться при вычислениях, записи алгебраических выражений, построении графиков и т. п. Функция пользователя определяется
Имя(список аргументов) := Выражение
Сначала задается имя функции, в круглых скобках указывается список аргументов функции (перечень используемых переменных), разделяемых запятыми. Затем вводится оператор присваивания. Справа от него записывается выражение, содержащее доступные системе операторы, операнды и функции с аргументами, указанными в списке аргументов.
Обращение к функции осуществляется по ее имени с подстановкой на место аргументов констант, переменных, определенных до обращения к функции, и выражений.
Основные виды графиков и инструменты для работы с ними находятся на палитре математических инструментов Graph (График).
Для построения графика функции одной переменной в декартовой системе координат в Mathcad:
- определяется функция пользователя;
- задается ранжированная переменная на некотором диапазоне с мелким шагом;
- вставляется шаблон двумерного графика X-Y Plot
;
- в знакоместо по оси абсцисс записывается имя переменной, а в знакоместо по оси ординат — функция или имя ранее определенной функции;
- производится щелчок левой клавишей мыши вне области графика.
Примечание — Для построения в одной координатной плоскости графиков двух и более функций их имена или определяющие выражения перечисляются в знакоместе по оси ординат через запятую.
Массив в пакете Mathcad – это совокупность конечного числа упорядоченных пронумерованных элементов, которая может иметь уникальное имя. Обычно используют одномерные (векторы) и двумерные (матрицы) массивы, содержащие числовые, символьные или строковые данные.

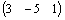
Порядковый номер элемента называется индексом. Местоположение элемента в массиве задается одним индексом для вектора и двумя – для матрицы. Номер первого элемента массива определяется значением системной переменной ORIGIN. По умолчанию ORIGIN = 0 и может принимать только целые значения. Изменение значения этой системной переменной осуществляется последовательностью команд Math / Options… / Built-In Variables / Array Origin (ORIGIN) (Математика / Параметры / Встроенные переменные / Начальный индекс массивов) или переопределением в документе, например:
Существует несколько способов создания массивов.
1-й способ. Использование панели Matrix (Матрицы).
Сначала набирается имя массива и оператор присваивания, например, 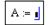
Далее указываем количество ее строк m (Rows) и столбцов n (Columns) матрицы. Для векторов один из этих параметров должен быть равен 1. При m = 1 получим вектор-строку, а при n = 1 – вектор-столбец.
На месте курсора появится шаблон, в знакоместа которого вводятся значения элементов массива:
2-й способ. Использование ранжированной переменной.
Целочисленные ранжированные переменные используются для задания индексов и позволяют создавать массивы в следующем порядке:
- определяется системная переменная ORIGIN;
- задается ранжированная переменная (переменные) для нумерации элементов;
- индексированной переменной присваиваются значения элементов массива через запятую или в виде явной формулы.
Обращаться к отдельным элементам вектора или матрицы можно, используя нижний индекс, принимающий только целочисленные значения. Для ввода нижнего индекса после имени вектора или матрицы нажимается клавиша «[» (прямая открывающая скобка) либо используется пиктограмма 
Для работы с векторами и матрицами система Mathcad имеет ряд специальных операторов и команд (представленных в таблице 1), используя которые не следует забывать об общих правилах матричного исчисления.
Таблица 1 – Команды палитры инструментов Matrix (Матрица)
📹 Видео
Основные действия с матрицами и векторами в MathCAD 14 (20/34)Скачать

MATLAB 04 Массивы и матрицыСкачать

Матрицы и векторыСкачать

МАТКАД МатрицыСкачать
Работа с массивами. Вектор столбцы и вектор строки 1. Урок 7Скачать

Математика это не ИсламСкачать

Матрицы и векторы. Настройки Mathcad при работе с матрицами. Урок 12Скачать

Собственные векторы и собственные значения матрицыСкачать

Матрицы в Mathcad(создание и редактирование матриц)(Урок 3.1)Скачать
Матрицы. Скалярное и векторное произведение векторов в Mathcad, матричные функции(Урок 3.3)Скачать
MathCAD Простейшие действия с матрицамиСкачать
Оператор векторизации в MathCAD 14 (23/34)Скачать

Векторы и матрицыСкачать
Программа MathCAD. Урок 10. Работа с матрицами в MathCADСкачать

Занятие 12. Векторы и матрицыСкачать

#11. Произведение матриц и векторов, элементы линейной алгебры | NumPy урокиСкачать

Создание матриц в MathCAD 14 (18/34)Скачать
















































































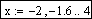
 ;
;