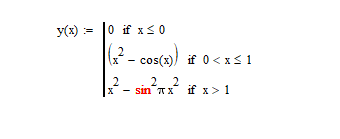Mathcad значение должно быть скалярным или вектором

Некоторые из операторов Mathcad имеют особые значения в применении к векторам и матрицам. Например, символ умножения означает просто умножение, когда применяется к двум числам, но он же означает скалярное произведение, когда применяется к векторам, и умножение матриц — когда применяется к матрицам.

Таблица описывает векторные и матричные операторы Mathcad. Многие из этих операторов доступны из палитры символов. Обратите внимание, что операторы, которые ожидают в качестве аргумента вектор, всегда ожидают вектор-столбец, а не вектор-строку.

Чтобы заменить вектор-строку на вектор-столбец, используйте оператор транспонирования [Ctrl]1.

Операторы, не перечисленные в этой таблице, не будут работать для векторов и матриц. При попытке использовать такой оператор с вектором или матрицей Mathcad будет отмечать это сообщением об ошибке “неверная операция с массивом”, или “нескалярная величина”. Можно, однако, использовать оператор векторизации, чтобы выполнить любую скалярную операцию или функцию поэлементно на векторе или матрице. См. раздел “Выполнение параллельных вычислений” ниже в этой главе. Рисунок 9 показывает использование некоторых векторных и матричных операций.

Рисунок 9: Векторные и матричные операции.

В следующей таблице

• A и B представляют массивы (векторы или матрицы).
• u и v представляют векторы.
• M представляет квадратную матрицу.
• и представляют отдельные элементы векторов u и v.
• z представляет скаляр.
• m и n представляют целые числа.

Операция	Обозначение	Клавиши	Описание
Умножение матрицы на скаляр		*	Умножает каждый элемент A на скаляр z.
Скалярное произведение		*	Возвращает скаляр: . Векторы должны иметь одинаковое число элементов.
Матричное умножение		*	Возвращает произведение матриц A и B, число столбцов в A должно соответствовать числу строк в B.
Умножение матрицы на вектор		*	Возвращает произведение матриц A и v, число столбцов в A должно соответствовать числу строк в v.
Деление		/	Делит каждый элемент массива на скаляр z.
Сложение векторов и матриц	A + B	+	Складывает соответствующие элементы A и B, массивы A и B должны иметь одинаковое число строк и столбцов.
Скалярная сумма	A + z	+	Добавляет z к каждому элементу A.
Векторное и матричное вычитание	A — B	—	Вычитает соответствующие элементы массива A из элементов массива B, массивы A и B должны иметь одинаковые размеры.
Скалярное вычитание	A — z	—	Вычитает z из каждого элемента A.
Изменение знака	— A	—	Умножает все элементы A на -1.
Степени матрицы, обращение матриц	M n	^	n-ная степень квадратной матрицы M (использует умножение матриц). n должен быть целым числом. M -1 представляет матрицу, обратную к M, другие отрицательные степени — степени обратной матрицы. Возвращает матрицу.
Длина вектора	|v|	|	Возвращает , где — вектор, комплексно сопряженный к v.
Детерминант	|M|	|	Возвращает детерминант квадратной матрицы M, результат — скаляр.
Транспонирование	A T	[Ctrl]1	Возвращает матрицу, чьи строки — столбцы А, и чьи столбцы — строки A. А может быть вектором или матрицей.
Векторное произведение	u x v	[Ctrl]8	Возвращает векторное произведение для векторов с тремя элементами u и v.
Комплексное сопряжение		«	Меняет знак мнимой части каждого элемента A.
Суммирование элементов		[Ctrl]4	Суммирует элементы вектора v; возвращает скаляр.
Векторизация		[Ctrl] —	Предписывает в выражении с A производить операции поэлементно. Полное описание дано в разделе “Выполнение параллельных вычислений”
Верхний индекс	A	[Ctrl]6	Извлекает n-ный столбец массива A. Возвращает вектор.
Нижний индекс (вектора)	vn	[	n-ный элемент вектора.
Нижние индексы матрицы	Am,n	[	Элемент матрицы, находящийся в m-ном ряду и n-ной строке.

Исправляем ошибки: Нашли опечатку? Выделите ее мышкой и нажмите Ctrl+Enter

Видео:Дискретные переменные в MathCAD 14 (9/34)Скачать

Значение должно быть скаляром, MathCad.

В примере, как работать с Маткадом, всё работает (изображение 1):

Когда я делаю тоже самое, появляется ошибка, что значения не является скаляром:

Как исправить? Помогите, пожалуйста.

Оно может быть скаляром, только если размеры матриц A и B совпадают.

Решение системы линейных уравнений — это ВСЕГДА вектор. Скаляром оно быть не может по определению.

В ошибочной строке справа после знака равенства есть какой-то символ перед В. Попробуй его убрать. Еще, этот самый знак равенства должен, похоже, вводиться через Ctrl =.

Видео:Скалярные и векторные величины, основные определения.Скачать

Маткад ошибка значение должно быть скалярным

Видео:Матрицы. Скалярное и векторное произведение векторов в Mathcad, матричные функции(Урок 3.3)Скачать

Маткад ошибка значение должно быть скалярным

БАЗОВЫЕ ОПЕРАЦИИ.
РАНЖИРОВАННЫЕ ПЕРЕМЕННЫЕ. ФУНКЦИИ. ГРАФИКИ
МАССИВЫ

1 Запуск. Формульные и текстовые области

Запуск Mathcad: Start / All Programs / Mathsoft Apps / Mathcad (Пуск / Все программы / Mathsoft Apps / Mathcad).

Документ Mathcad просматривается, интерпретируется и выполняется слева направо и сверху вниз и может включать три вида областей:

Для ввода математических символов: View / Toolbars / Math (Вид / Панели инструментов / Математическая).

Каждое математическое выражение набирается в отдельной формульной области. Одна формула – одна область!

Перемещение курсора — клавиша Пробел. Изменение направления уголка — клавиша Insert (Ins).

«:=» — «присвоить» — задать выражение (число или формулу)

«=» — «вычислить» подсчитать и вывести значение выражения.

Для вставки в документ текстовой области выполняют Insert / Text Region (Вставка / Область текста), либо просто нажимают в формульной области Пробел. Текстовая область имеет рамку с маркерами, позволяющими изменять ее размеры, и курсор в виде вертикальной линии красного цвета.

2 Ранжированные переменные. Функции. Графики

В Mathcad существует тип переменных, принимающих не одно, а множество значений. Такие переменные носят название ранжированных или дискретных. Ранжированная переменная – переменная, которая принимает ряд значений при каждом ее использовании, причем каждое значение отличается от соседнего на постоянную величину, называемую шагом.

Ранжированная переменная общего вида определяется выражением:

Имя := x1, x2 .. xn

Здесь Имя – задаваемое пользователем имя ранжированной переменной;
x1 – первое значение ранжированной переменной;
x2 – второе значение ранжированной переменной (x2 = x1 + Dx — первое значение плюс шаг);
xn – последнее значение ранжированной переменной.
Значения x1 и x2 разделяются запятой, двоеточие представляет собой единый оператор, указывающий на изменение переменной в заданных пределах. Он вводится с клавиатуры клавишей «;» или выбирается с палитры математических инструментов Matrix (Векторы и матрицы) (кнопка — Range Variable).

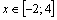
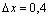
Например, если переменная изменяется в интервале с шагом , то она задается в виде

Шаг изменения значений ранжированной переменной в явном виде обычно не задается, он определяется как x2 – x1.

Функции в системе Mathcad можно условно разделить на две группы: встроенные и функции пользователя. Встроенные функции изначально заданы в системе разработчиками. Имя функции вводится с клавиатуры, обычно в нижнем регистре. Полный перечень встроенных функций можно получить, выполнив команду Function (Функция) главного меню Insert (Вставка), или нажав на кнопку панели инструментов. При этом появляется окно, где справа перечислены возможные категории функций, а слева – список функций из выделенной категории.

Среди наиболее часто используемых функций можно указать:

• sin(z) — синус z (z задается в радианах);
• cos(z) — косинус z;
• tan(z) — тангенс z;
• cot(z) — котангенс z;
• exp(z) – экспоненциальная функция, значение е (основание натурального логарифма) в степени z;
• ln(z) – натуральный логарифм z;
• log(z) – десятичный логарифм числа z;
• log(z, b) – логарифм числа z по основанию b;
• acos(z) – арккосинус z;
• acot(z) – арккотангенс z;
• asin(z) – арксинус z;
• atan(z) – арктангенс z.

Функция пользователя сначала должна быть определена, а затем к ней можно обращаться при вычислениях, записи алгебраических выражений, построении графиков и т. п. Функция пользователя определяется

Имя(список аргументов) := Выражение

Сначала задается имя функции, в круглых скобках указывается список аргументов функции (перечень используемых переменных), разделяемых запятыми. Затем вводится оператор присваивания. Справа от него записывается выражение, содержащее доступные системе операторы, операнды и функции с аргументами, указанными в списке аргументов.

Обращение к функции осуществляется по ее имени с подстановкой на место аргументов констант, переменных, определенных до обращения к функции, и выражений.

Основные виды графиков и инструменты для работы с ними находятся на палитре математических инструментов Graph (График).

Для построения графика функции одной переменной в декартовой системе координат в Mathcad:

1. определяется функция пользователя;
2. задается ранжированная переменная на некотором диапазоне с мелким шагом;
3. вставляется шаблон двумерного графика X-Y Plot;
4. в знакоместо по оси абсцисс записывается имя переменной, а в знакоместо по оси ординат — функция или имя ранее определенной функции;
5. производится щелчок левой клавишей мыши вне области графика.

Примечание — Для построения в одной координатной плоскости графиков двух и более функций их имена или определяющие выражения перечисляются в знакоместе по оси ординат через запятую.

Массив в пакете Mathcad – это совокупность конечного числа упорядоченных пронумерованных элементов, которая может иметь уникальное имя. Обычно используют одномерные (векторы) и двумерные (матрицы) массивы, содержащие числовые, символьные или строковые данные.

– вектор-столбец; – вектор-строка.

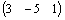
Порядковый номер элемента называется индексом. Местоположение элемента в массиве задается одним индексом для вектора и двумя – для матрицы. Номер первого элемента массива определяется значением системной переменной ORIGIN. По умолчанию ORIGIN = 0 и может принимать только целые значения. Изменение значения этой системной переменной осуществляется последовательностью команд Math / Options… / Built-In Variables / Array Origin (ORIGIN) (Математика / Параметры / Встроенные переменные / Начальный индекс массивов) или переопределением в документе, например:

Существует несколько способов создания массивов.

1-й способ. Использование панели Matrix (Матрицы).

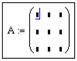
Сначала набирается имя массива и оператор присваивания, например, 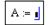. Далее на панели Math (Математика) выбираем кнопку Matrix (Матриц):

Далее указываем количество ее строк m (Rows) и столбцов n (Columns) матрицы. Для векторов один из этих параметров должен быть равен 1. При m = 1 получим вектор-строку, а при n = 1 – вектор-столбец.

На месте курсора появится шаблон, в знакоместа которого вводятся значения элементов массива:

2-й способ. Использование ранжированной переменной.

Целочисленные ранжированные переменные используются для задания индексов и позволяют создавать массивы в следующем порядке:

1. определяется системная переменная ORIGIN;
2. задается ранжированная переменная (переменные) для нумерации элементов;
3. индексированной переменной присваиваются значения элементов массива через запятую или в виде явной формулы.

Обращаться к отдельным элементам вектора или матрицы можно, используя нижний индекс, принимающий только целочисленные значения. Для ввода нижнего индекса после имени вектора или матрицы нажимается клавиша «[» (прямая открывающая скобка) либо используется пиктограмма 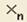с палитры математических инструментов Matrix. Для элемента матрицы указываются через запятую два индекса, обозначающих номер строки и номер столбца соответственно.

Для работы с векторами и матрицами система Mathcad имеет ряд специальных операторов и команд (представленных в таблице 1), используя которые не следует забывать об общих правилах матричного исчисления.

Таблица 1 – Команды палитры инструментов Matrix (Матрица)

Видео:7. MathCad. Векторы и матрицыСкачать

Задача 44319 Не могу понять в чём ошибка. Приложение

УСЛОВИЕ:

Не могу понять в чём ошибка. Приложение пишет, что значение должно быть скалярным. Это MathCad 15.0. Что нужно сделать, чтобы исправить ошибку?

РЕШЕНИЕ ОТ slava191 ✪ ЛУЧШЕЕ РЕШЕНИЕ

Возможно нужно взять аргументы sin в круглые скобки sin(Pix^2)

Возможно, также, что mathcad не знает что такое Pi и перед всей конструкцией надо написать Pi:=3,14

Добавил vk140758054 , просмотры: ☺ 48 ⌚ 2020-02-17 11:10:37. информатика 1k класс

Решения пользователей

Написать комментарий

В прошедшем году страна имела следующие показатели, ден. ед.: ВНП — 500; чистые инвестиции частного сектора — 75; государственные закупки — 80; потребление домашних хозяйств — 250; поступление в государственный бюджет прямых налогов — 30; косвенных — 20; субвенции предпринимателям — 25; экспорт — 150; импорт — 110.
Определить:
а) располагаемый доход домашних хозяйств;
б) амортизационный фонд (D);
в) состояние государственного бюджета.

а) Определим величину НД на основе данных о его использовании
у = 250 + 75 + 80 + 150 – 110 = 445.

Поскольку прямые налоги составляют 30 ден. ед., то располагаемый доход:
yv = 445 – 30 = 415.

б) Амортизационный фонд (D) соответствует разности (ВНП— ЧНП). В свою очередь ЧНП = 445 + 20 – 25 = 440.
Следовательно, D = 500 – 440 = 60.

в) Состояние госбюджета характеризуется разностью между государственными расходами и поступлениями в бюджет
δ= (80 + 25) – (30 + 20) = 55.
ТОЛЬКО ПОДСТАВЬ СВОИ ЦИФРЫ.

опираться на традиционный подход, при котором учитывается, что окончания, как и другие морфемы, являются двусторонними единицами, то есть имеют не только форму, но и значение. Окончания имеют грамматические значения, которые характеризуют словоформу как принадлежащую к определенному классу и обязательны для всех словоформ данного класса. Окончания с одним и тем же грамматическим значением считаются одинаковыми, даже если не полностью совпадают по звуко-буквенному оформлению. Так, традиционно считается, что в словоформах большой (книги) и синей (книги) одно и то же окончание, потому что оно выражает одно и то же грамматическое значение (ж.р., ед.ч., Р.п.) и при этом представлено в словах одного грамматического класса — прилагательных. Различия в произношении и в написании (-ой и -ей) связаны с тем, что во втором прилагательном основа заканчивается на мягкий согласный. При совпадающем произношении и написании окончания считаются разными, если выражают разные грамматические значения. Так, в словоформах большой (дом), большой (книги), (к) большой (книге), большой (книгой), (о) большой (книге) окончания разные — омонимичные, так как при внешнем совпадении они выражают разные грамматические значения: большой (дом) — м.р., ед.ч., И.п., большой (книги) — ж.р., ед.ч., Р.п., (к) большой (книге) — ж.р., ед.ч., Д.п., большой (книгой) — ж.р., ед.ч., Т.п., (о) большой (книге) — ж.р., ед.ч., П.п.

Важным является также то, что каждое окончание всегда является элементом какого-либо набора окончаний, которые именно в противопоставлении друг другу реализуют свое значение. Рассмотрим словосочетания большой победой и большой столовой. У прилагательного и существительного в словосочетании большой победой окончания разные, хотя внешне они совпадают и оба имеют значение ед.ч., Т.п. Дело в том, что каждое из этих окончаний противопоставлено разным единицам, является элементом разных наборов окончаний. Окончание ‑ой в большой противопоставлено другим окончаниям прилагательных, а -ой в победой противопоставлено другим окончаниям существительных первого склонения. Окончания прилагательного и существительного в словосочетании большой столовой считаются одинаковыми: хотя слово столовая является существительным, его окончания типичны для прилагательных[ii]. Оно сохранило часть набора окончаний прилагательного: имеет такие же окончания, как прилагательное в сочетании столовая комната.

С учетом сказанного выше можно выделить такие группы словоформ с одинаковыми окончаниями[iii]:

1. каша, семья, борода — окончания существительных 1 склонения в единственном числе, в И.п.;

2. кальций, стол, патриций — нулевые окончания существительных 2 склонения мужского рода в единственном числе, в И.п.;

3. море, сражение — окончания существительных 2 склонения среднего рода в единственном числе, в И.п.;

4. морей, людей — окончания существительных во множественном числе, в Р.п.;

5. синий, бледнолицый, большой, рабочий, нищий, заведующий – окончания прилагательных в мужском роде, в единственном числе, в И.п.;

6. большая, столовая, синяя — окончания прилагательных в женском роде, в единственном числе, в И.п.;

7. последние, красивые — окончания прилагательных во множественном числе, в И.п.

Приписав окончаниям указанные грамматические значения, мы получили 7 групп. Вне группы (если считать, что в группе должно быть больше одного элемента) оказались словоформы синей (окончание прилагательного в женском роде, в единственном числе, в Т. п.) и революцией (окончание существительного 1 склонения в единственном числе, в Т. п.).

Заметим, что при другом выборе значений из числа омонимичных можно получить другое разбиение на группы.

Видео:Основные действия с матрицами и векторами в MathCAD 14 (20/34)Скачать

Маткад ошибка значение должно быть скалярным

A «Find» or
«Minerr» must
be preceded
by a matching
«Given»

Find или Minerr
должны предва-
ряться ключе-
вым словам

Эта ошибка выде-
ляет функцию Find
или Minerr при их
несогласованности

Каждый вычислительный блок,
который заканчивается функцией
Find или Minerr, должен начи-
наться с ключевого слова Given

All evaluations
resulted in
either an error
or a complex
result

Вычисления
приводят к
ошибке или
комплексному
результату

MathCAD не может
начертить некото-
рые точки, потому
что не существует
действительных
значений для их
нанесения
на график

Это сообщение может появиться,
если имеется ошибка или все
значения комплексные

Arguments in
function
definitions
must be names

Аргументы
в определениях
функции
должны быть
именами

Выделенное опре-
деление функции
содержит непра-
вильный перечень
аргументов

В списке аргументов должны быть
правильно поименованы пере-
менные, или список имен необхо-
димо отделить запятыми

At least one
limit must
be infinity

По крайней
мере один пре-
дел должен
быть бесконеч-
ным

Когда для интегри-
рования выбран
алгоритм бесконеч-
ного предела, то по
крайней мере один
из пределов инте-
грала должен быть
бесконечным

Тип бесконечности вводится на-
жатием сочетания клавиш
+ + .

Для изменения алгоритма, ис-
пользующего бесконечный предел
или для вычисления какого-либо
другого интеграла, щелкните на
интеграле правой кнопкой мыши
и измените алгоритм с помощью
контекстного меню

Can only
evaluate an nth
order derivative
when n=0,1..5.

Можно вычис-
лить n-й поря-
док производ-
ной, только
когда п=0,1—5

Порядок производ-
ной должен быть
одним из следую-
щих чисел: 0, 1,
2,. ..5.

Если вы хотите посчитать произ-
водную более высокого порядка,
то делайте это с помощью сим-
вольного дифференцирования

Can’t evaluate
this function
when its
argument less
than or equal
to zero

Невозможно
вычислить эту
функцию, когда
ее аргумент
меньше или
равен нулю

Такое сообщение
может касаться
XY- или полярных
графиков, имеющих
логарифмические
оси, на которых или
пределы, или неко-
торые из значений,
не положительны

Отрицательные числа и ноль не
могут быть расположены нигде на
логарифмических осях. Смените
тип осей графика или постройте
его для других значений

Can’t converge
to a solution

Не сходится
к решению

Численный метод
расходится
(не может найти
решения)

Убедитесь, что операция не при-
меняется к функции в области
непосредственной близости точки
ее сингулярности (деления на
ноль).

Попробуйте поменять параметры
численного метода (например,
начальное приближение).

Попробуйте увеличить константу
TOL, т. е. осуществить поиск ре-
шения с худшей погрешностью.

Попробуйте поменять численный
алгоритм, если это возможно
(вызвав контекстное меню нажа-
тием на месте ошибки правой
кнопки мыши)

Can’t define
the same
variable more
than once in
the same
expression

Невозможно
определить ту
же самую пере-
менную более
одного раза в
одном и том же
выражении

Вы пытаетесь вы-
числить одну и ту
же переменную
дважды в одном
выражении

Пример подобной ошибки: если
вы создаете вектор с левой сто-
роной а := и используете это же
имя справа, то получите ошибку

Can’t
determine what
units the result
of this
operation
should have

Невозможно
определить, в
каких единицах
следует быть
результату этой
операции

Вы возвели выра-
жение, содержащее
единицы измере-
ния, в степень, яв-
ляющуюся пере-
менной в неких
пределах или век-
тором. В результате
невозможно опре-
делить размерность
результата

Если выражение включает в себя
единицы измерений, то можно
возводить его только в действи-
тельную фиксированную степень

Видео:18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать

Маткад ошибка значение должно быть скалярным

MathCAD — это просто! Часть 27. Программирование и ошибки: вместе веселее!

Что ж, хотя мы уже немало всего успели обсудить насчет программирования в такой замечательной математической среде, как MathCAD, еще немало весьма существенных тем осталось за кадром. И, пожалуй, самая существенная из них — это взаимодействие начинающего программиста, пишущего программы в MathCAD’е, и ошибок в его программах. Именно на ней мы с вами сейчас и остановимся.

В общем-то, если сказать, что ошибки никто не любит, это будет не так уж далеко от истины. Точнее, никто не любит собственные ошибки. Чужие любят все, а не только экзаменаторы и разнообразные инспекторы. Однако, к сожалению, при программировании (а написание небольших вспомогательных программок в MathCAD’е, как я уже когда-то давно тому назад говорил, это тоже программирование) ошибки попросту неизбежны. Даже самые лучшие программисты совершают ежедневно множество ошибок, и никто, в общем-то, за это не применяет к ним особых санкций. Существует даже такое мнение, что программа без ошибок совершенно бесполезна — если в ней нет ошибок, значит, в ней нет и никакой полезной функциональности, потому что не ошибается только тот, кто ничего не делает. Так что ошибки в программах — это вполне естественные спутники каждого, кто пишет даже самые маленькие программки, а потому и бояться их не следует. Тем не менее, с ошибками в программах можно и нужно бороться. И для этого существуют специальные средства, некоторые из которых доступны и тем, кто пишет программы в MathCAD’е. Однако, прежде чем рассказывать о том, что это за средства, и как ими нужно пользоваться, нужно, как мне лично кажется, поговорить еще немного о том, вокруг чего будет сосредоточена наша борьба — то есть о самих ошибках.

Поскольку, как я уже говорил, ошибки довольно многочисленны, их имеет смысл классифицировать. Сделать это стоит, в общем-то, уже хотя бы попросту потому, что разные виды ошибок требуют различных к себе подходов, и их устранение требует вложения различного количества труда того, кто писал программу.

Самые простые ошибки — синтаксические. Как вы уже имели возможность воочию убедиться, при программировании очень важно придерживаться определенных правил в записи конструкций. Например, если вы вместо имени функции rkfixed напишете в программе tkfixed, ошибившись при вводе на одну букву и нажав на соседнюю с r клавишу t, то как раз и получите в свое распоряжение самую что ни на есть классическую синтаксическую ошибку. Ни к каким особенно страшным последствиям она (как, впрочем, и все другие ошибки аналогичного класса) не приведет: программа просто не сможет быть выполнена по той причине, что MathCAD не сможет найти функцию, которую вы ему указали. Искать такие ошибки тоже совсем не сложно — они всегда хорошо видны, поскольку даже сама среда подсвечивает их, чтобы можно было найти особенно быстро. Исправлять, соответственно, тоже очень просто: достаточно записать идентификатор правильно, и все в программе станет на положенные места. MathCAD, кстати, избавляет пользователя от множества таких ошибок благодаря необходимости вводить все операторы, управляющие ходом программы, с помощью специальных горячих клавиш или соответствующих кнопок на панели инструментов Программирование. Если бы их нужно было, напротив, набирать вручную с клавиатуры, то и возможности сделать синтаксическую ошибку были бы несравнимо шире.

Второй тип ошибок — ошибки алгоритмические. Это такие ошибки, которые, в принципе, не мешают выполнению программы, но делают результаты такого выполнения полностью лишенными всякого смысла. Многие из таких ошибок — банальные опечатки: там, где нужно было поставить плюс, вы, например, поставили в спешке минус или же сделали что-нибудь другое примерно в таком же духе. Конечно, сказать, что алгоритмические ошибки — это сплошь и рядом одни только опечатки, было бы, мягко говоря, не до конца верно. Потому что очень многие из них являются следствием недостаточности знаний писавшего программу — то есть если ошибочно составлена сама последовательность действий, которые должен сделать MathCAD для того, чтобы вы могли получить интересующий вас результат. Еще великое множество алгоритмических ошибок — результат банальной невнимательности: например, присвоение значения не той переменной, ее необнуление либо, например, вывод не той переменной в качестве результата выполнения вашей программы. В общем-то, именно об алгоритмических ошибках мы с вами сейчас и будем говорить более подробно. Однако есть еще один, особенно неприятный, тип ошибок.

Третий тип — это ошибки мистические. Да-да, именно мистические, я не оговорился. Какие именно это ошибки? Это ошибки, имеющие совершенно непонятную природу и столь же непонятный способ лечения — как правило, это проявления ошибок не в вашей программе, а в каком-то из внутренних компонентов MathCAD’а. К сожалению, эти ошибки, в «большом» программировании встречающиеся не так уж, в общем-то, и часто, в MathCAD’е не такие уж редкие гости. Отчасти это объясняется тем, что MathCAD — это все-таки средство расчетов, а не программирования, которое играет в этой среде второстепенную и вспомогательную роль, но, конечно, когда реально сталкиваешься с такими вот мистическими ошибками, это все не слишком успокаивает. Хотя поначалу почти все ошибки в программах кажутся мистическими, на самом деле большая их часть все-таки имеет рациональную природу. Если же природа появившейся ошибки вам совершенно непонятна, то вам следует коренным образом перестроить структуру программы или хотя бы тот ее фрагмент, в котором локализовалось проявление этой ошибки. Практически во всех случаях этот не слишком хитрый прием позволяет полностью избавить программу от досадной непонятной ошибки.

Что ж, о самих ошибках мы с вами, можно считать, побеседовали. Теперь давайте, пожалуй, перейдем к тому, какими именно способами можно бороться с самыми распространенными из них — то есть алгоритмическими. Об остальных, в общем-то, я уже довольно подробно все рассказал, а вот что касается алгоритмических ошибок, то здесь нужно будет в большинстве случаев прибегнуть к помощи специализированных встроенных в MathCAD инструментов.

Отладка в MathCAD’е

Процесс поиска и устранения алгоритмических ошибок называется по-русски отладкой. По-английски этот же самый процесс называется debugging, то есть, если дословно, «избавление от жучков». В общем-то, и по-русски довольно часто можно услышать термины «дебагинг» или «баг», однако во избежание путаницы мы будем использовать слово «отладка» (если, конечно, не возражаете). Кстати, история возникновения английского термина весьма любопытна, и, вполне возможно, вы ее слышали. Первые компьютеры были машинами весьма громоздкими и дорогостоящими, а потому и всевозможные поломки для них были делом далеко не просто устранимым. Когда выяснилось, что причиной очередной поломки стал жучок, забравшийся внутрь компьютера и вызвавший замыкание, в счете за ремонт записали: «debugging». Рука шутника оказалась легкой — термин, как видите, прижился и используется на протяжении уже многих десятилетий.

В чем же заключается процесс отладки? На самом деле ничего особенно таинственного и трудного для понимания здесь нет. Просто во время отладки у вас есть возможность выполнять программу не сразу «залпом», как это происходит обычно, а пошагово, то есть выполнять последовательно друг за другом каждую строчку программы, делая, когда нужно, паузы для осмысления работы программы и просмотра промежуточных значений каждой из переменных. Отладка используется при разработке любых программ, а потому и создатели MathCAD включили поддержку этого удобного и, в общем-то, достаточно универсального средства выявления ошибок в свой программный продукт. Доступ к инструментам, используемым при отладке программ в MathCAD’е, осуществляется через подпункт Debug меню Tools в главном рабочем окне MathCAD’а (см. соответствующий скриншот).

Стоит отметить, что, поскольку MathCAD — это среда, ориентированная не на программирование, а на различные вычислительные действия, то отладка в ней имеет более широкое применение, чем только отладка программ, которые пишет пользователь. Отлаживать можно и все вычисления даже в том случае, если они выполняются без применения какого-либо программирования с вашей стороны. В общем-то, поскольку такая возможность будет весьма полезной для большинства читателей не столько при программировании в MathCAD’е, сколько при обычных вычислениях, то именно с такой позиции мы с вами и станем рассматривать отладку в этой мощной математической среде. Нам также понадобится панель отладки. Ее включают так же, как все остальные панели инструментов, в меню View -> Toolbars. Конечно, эта панель, как вы могли уже заметить, дублирует отладочное меню в Tools -> Debug, однако, думаю, нажать на кнопку, расположенную на этой панели, будет все-таки проще и быстрее, чем искать соответствующий пункт в надежно спрятанном от пользователя меню.

При переходе в отладочный режим (кнопка либо пункт меню Toggle Debug Mode) внешний вид главного окна MathCAD’а меняется (см. скриншот): внизу появляется специальное окно, используемое для просмотра промежуточной отладочной информации. Оно называется Trace Window.

Однако о том, что именно отображается в этом самом окне, а также о том, что от нас требуется сделать с документом перед тем, как его можно будет уже полноценно отлаживать, мы с вами поговорим, пожалуй, в следующий раз, чтобы не перегружать вас разнообразной полезной информацией. Сейчас же подведем итоги разговора про ошибки, возникающие в процессе написания программ в математической среде MathCAD.

Как видите, ошибок в программах действительно бояться не следует. Это вполне нормальная составляющая процесса программирования, неизбежно проявляющаяся в каждом из результатов этого процесса. Тем не менее, с ошибками можно и нужно бороться, и с большинством из них это можно производить с весьма высокой вероятностью достижения успеха. Хотя, конечно же, встречаются и такие ошибки, с которыми трудно будет разобраться даже тому, кто на программировании, что называется, собаку съел. Но все-таки они встречаются не так уж часто. Так что в программировании, если вы хотите избежать мучений, связанных с поиском ошибок, очень важна ваша внимательность. Если вы будете достаточно внимательны при написании программы, то риск допустить ошибку будет сравнительно невелик. Впрочем, это правило применимо не только к программированию.

Видео:Скалярное произведение векторов. 9 класс.Скачать

Обработка ошибок.

Система MathCAD предоставляет пользователю некоторый контроль над ошибками, которые могут возникнуть при вычислении выражений или при выполнении программ. Для этой цели служит оператор on error, который можно вставить с помощью одноименной кнопки панели Programming . В поле ввода справа следует ввести выражение или программу, которые необходимо вычислить (известно, что это выражение может содержать ошибку при определенных значениях входных параметров). В поле ввода слева следует ввести выражение, которое будет выполнено вместо правого выражения, если при выполнении последнего возникнет ошибка. Пример: Если аргументу функции присвоено нулевое значение, то в программе возникает ошибка — деление на нуль. Но за счет оператора on error сообщение не выводится, а функции в этой точке присваивается значение, указанное слева от оператора on error — значение машинной бесконечности.

В поле ввода слева может быть введено текстовое выражение, сообщающее об ошибке

Конечно, если программа содержит только простейшие математические операции, то никаких ошибок, кроме деления на нуль или превышения наибольшего допустимого числа в ней возникнуть не может. В таких программах оператор on error используется редко. Но для более сложных программ, которые содержат функции решения дифференциальных уравнений, аппроксимации или другие сложные функции MathCAD, использование on error может избавить от многих трудностей.

Иногда может возникнуть ситуация обратная той, которая была описана выше, т.е. необходимо, чтобы при определенных условиях результатом выражения было сообщение об ошибке, хотя в действительности при этом не возникает ни одной стандартной ошибки MathCAD. Для таких случаев в MathCAD предусмотрена встроенная функция error. В качестве аргумента этой функции нужно в кавычках указать текст сообщения об ошибке, который должен быть выведен. Таким образом, если необходимо, чтобы программа возвращала ошибку при определенном условии, то следует использовать конструкцию вида: error («текст ошибки») if (условие).

Для того, чтобы иметь возможность нормально вводить текст на русском языке в аргумент функции error (а также во все другие функции со строками), следует изменить шрифт, который используется во встроенном стиле Constant. Для того чтобы этот стиль правильно отображал русские буквы, установите курсор на любом числе или строковом выражении в формульном блоке. При этом в поле на панели инструментов Formatting, отображающем текущий стиль, должно быть написано — Constant. Теперь выберите из раскрывающегося списка шрифтов шрифт, поддерживающий кириллицу.

1. Вычислить функцию sin(x) с точностью е.

2. Даны массивы А(5) и В(5). Получить массив С, в который записаны сначала элементы

массива А в порядке возрастания, а затем элементы массива В порядке убывания

3. По введенным значениям коэффициентов А, В, С определить корни квадратного уравнения

4. Дан массив натуральных чисел В(10). Определить, есть ли в нем 4 последовательных числа (например, 1, 2, 3, 4, и т.п.). Напечатать такие группы чисел.

1. Какая панель служит для вставки программного кода в документ MathCAD? Можно ли операторы программирования набрать с клавиатуры?

2. С какой команды начинается создание программного блока? Как с ее помощью можно создавать разветвленный программный блок?

3. Что такое определение программного блока? Обращение к программному блоку?

4. Что такое глобальные и локальные переменные для программного блока? Что может содержать последняя строка программного блока?

5. Как работает оператор if в программном блоке? Приведите пример.

6. Создание цикла с параметром в программном блоке. Приведите пример.

7. Создание цикла while в программном блоке. Приведите пример.

8. Для чего служат операторы break, continue в программном блоке? Приведите примеры.

9. Как работает оператор return в программном блоке? Приведите пример.

10. Как осуществляется обработка ошибок в программном блоке? Приведите пример.

💥 Видео

Новое задание профиля №2. Все, что нужно знать о векторах | Аня МатеманяСкачать

7.5 ЧАСОВ МАТАНА!!! ПОДАРОК ВСЕМ СТУДЕНТАМ ДЛЯ ПОДГОТОВКИ К ЗАЧЁТАМ И ЭКЗАМЕНАМ ОТ ЁЖИКА В МАТАНЕ!!!Скачать

Математика без Ху!ни. Свойства скалярного и векторного произведений.Скачать

1. MathCad. Вычисление значений числовых выраженийСкачать

Все типы 2 задание векторы ЕГЭ по математике профиль 2024Скачать

СКАЛЯРНОЕ УМНОЖЕНИЕ ВЕКТОРОВ ЧАСТЬ I #математика #егэ #огэ #формулы #профильныйегэ #векторыСкачать

2. MathCad. Операции относительно заданной переменнойСкачать

Сравнение скалярного и векторного произведений векторов (видео 16) | Магнетизм | ФизикаСкачать

Как выражать вектор? Как решать задачу с вектором? | TutorOnlineСкачать

Урок 3. Произведение векторов и загадочный угол между векторами. Высшая математика | TutorOnlineСкачать

Лекция 18. Скалярное произведение векторов и его свойства.Скачать

9 класс, 20 урок, Свойства скалярного произведения векторовСкачать

Математика без Ху!ни. Угол между векторами, применение скалярного произведения.Скачать
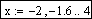