В случае многомерной случайной величины (случайного вектора) характеристикой разброса ее составляющих и связей между ними является ковариационная матрица.
Ковариационная матрица определяется как математическое ожидание произведения центрированного случайного вектора на тот же, но транспонированный вектор:
где
Ковариационная матрица имеет вид
где по диагонали стоят дисперсии координат случайного вектора on=DXi, o22=DX2, окк = DXk, а остальные элементы представляют собой ковариации между координатами
Ковариационная матрица является симметрической матрицей, т.е.
Для примера рассмотрим ковариационную матрицу двумерного вектора
Аналогично получается ковариационная матрица для любого /^-мерного вектора.
Дисперсии координат можно представить в виде
где Gi,C2. 0? — средние квадратичные отклонения координат случайного вектора.
Коэффициентом корреляции называется, как известно, отношение ковариации к произведению средних квадратичных отклонений:
После нормирования по последнему соотношению членов ковариационной матрицы получают корреляционную матрицу
которая является симметрической и неотрицательно определенной.
Многомерным аналогом дисперсии случайной величины является обобщенная дисперсия, под которой понимается величина определителя ковариационной матрицы
Другой общей характеристикой степени разброса многомерной случайной величины является след ковариационной матрицы
где т — вектор-столбец математических ожиданий;
|Х| — определитель ковариационной матрицы X;
? -1 — обратная ковариационная матрица.
Матрица X -1 , обратная к матрице X размерности пх п, может быть получена различными способами. Одним из них является метод Жордана—Гаусса. В этом случае составляется матричное уравнение
где х — вектор-столбец переменных, число которых равно я; b — я-мерный вектор-столбец правых частей.
Умножим слева уравнение (6.21) на обратную матрицу ХГ 1 :
Так как произведение обратной матрицы на данную дает единичную матрицу Е, то
Если вместо b взять единичный вектор
то произведение X -1 -ех дает первый столбец обратной матрицы. Если же взять второй единичный вектор
то произведение Е 1 е2 дает первый столбец обратной матрицы и т.д. Таким образом, последовательно решая уравнения
методом Жордана—Гаусса, получаем все столбцы обратной матрицы.
Другой метод получения матрицы, обратной к матрице Е, связан с вычислением алгебраических дополнений AtJ.= (/= 1, 2. п; j = 1, 2, . п) к элементам данной матрицы Е, подстановкой их вместо элементов матрицы Е и транспортированием такой матрицы:
Обратная матрица получается после деления элементов В на определитель матрицы Е:
Важной особенностью получения обратной матрицы в данном случае является то, что ковариационная матрица Е является слабо обусловленной. Это приводит к тому, что при обращении таких матриц могут возникать достаточно серьезные ошибки. Все это требует обеспечения необходимой точности вычислительного процесса или использования специальных методов при вычислении таких матриц.
Пример. Написать выражение плотности вероятности для нормально распределенной двумерной случайной величины <Xv Х2)
при условии, что математические ожидания, дисперсии и ковариации этих величин имеют следующие значения:
Решение. Обратную ковариационную матрицу для матрицы (6.19) можно получить, используя следующее выражение обратной матрицы к матрице X:
где А — определитель матрицы X.
Аи, Л12, А21, А22 — алгебраические дополнения к соответствующим элементам матрицы X.
Тогда для матрицы ]г- ! получаем выражение
Так как а12 = 01О2Р и °2i =a 2 a iP> а a i2 a 2i = cyfст|р, то 

Функция плотности вероятности запишется в виде
Подставив исходные данные, получим следующее выражение для функции плотности вероятности
Видео:Математическое ожидание-3 типа задачСкачать

3.3 Математические ожидания и ковариации векторов и матриц
3.3. Математические ожидания и ковариации векторов и матриц
При работе с линейными моделями удобно представлять данные в виде векторов или матриц. Элементы некоторых векторов или матриц статистических линейных моделей являются случайными переменными. Определение случайной переменной было дано. Значение этой переменной зависит от случайного результата опыта.
В этой книге рассматривается такой тип векторов случайных переменных отклика, элементы которого могут быть коррелированы, а влияющие на них переменные являются контролируемыми и неслучайными. В конкретной линейной модели, влияющие на отклик переменные, имеют выбранные или полученные в результате расчёта детерминированные значения. Таким образом, в рассматриваемых линейных моделях имеются два вектора случайных переменных:
у= 

Значения i-й переменной уi (i=1, 2, …, n) отклика наблюдаются в результате проведения i-го опыта эксперимента, а значения переменной ei случайной ошибки не наблюдаются, но могут оцениваться по наблюдаемым значениям переменной отклика и значениям влияющих на неё переменных.
При рассмотрении линейных моделей широко используются векторы и матрицы случайных переменных, поэтому в первую очередь для них необходимо обобщить идеи математического ожидания, ковариации и дисперсии.
Математическое ожидание вектора у размеров пх1 случайных переменных y1, y2, . уп определяется как вектор их ожидаемых значений:
Е(у)=Е


Видео:Математика без Ху!ни. Ряд распределения дискретной случайной величины. Мат ожидание и дисперсия.Скачать

Рекомендуемые файлы
где E(уi)=yi получается в виде E(уi)=
Если х и у — векторы случайных переменных размеров пх1, то, в силу (3.3.1) и (3.2.7), математическое ожидание их суммы равно сумме их математических ожиданий:
Пусть уij (i=1, 2, . m; j=1, 2, . п) набор случайных переменных с ожидаемыми значениями E(уij). Выражая случайные переменные и их математические ожидания в матричной форме, можно определить общий оператор математического ожидания матрицы Y=(yij) размеров mхп следующим образом:
Определение 3.3.1. Математическое ожидание матрицы Y случайных переменных равно матрице математических ожиданий её элементов
По аналогии с выражением (3.3.1), ожидаемые значения матрицы Y случайных переменных представляются в виде матрицы ожидаемых значений:
E(Y)=

Вектор можно рассматривать как матрицу, следовательно, определение 3.3.1 и следующая теорема справедливы и для векторов.
Теорема 3.3.1. Если матрицы А=(аij) размеров lхm, B=(bij) размеров nхp, С=(cij) размеров lхp – все имеют элементами постоянные числовые значения, а Y – матрица размеров mхn случайных переменных, то
Доказательство дано в книгах [Себер (1980) стр.19; Seber, Lee (2003) стр.5]
Там же доказывается, что, если матрицы A и В размеров mхn, элементами которых являются постоянные числовые значения, а х и у — векторы случайных переменных размеров пх1, то
Если f(Y) – линейная функция матрицы Y, то её ожидаемое значение находится по формуле Е[f(Y)]=f[Е(Y)] [Boik (2011) cтр.134]. Например, если матрицы А размеров рхm, B размеров пхр и С размеров рхр — все имеют элементами постоянные числовые значения, а матрица Y размеров тхп случайных переменных, то
Ковариации и дисперсии
Аналогичным образом можно обобщить понятия ковариации и дисперсии для векторов. Если векторы случайных переменных х размеров mх1 и у размеров nх1, то ковариация этих векторов определяется следующим образом.
Определение 3.3.2. Ковариацией векторов х и у случайных переменных является прямоугольная матрица ковариаций их элементов
Теорема 3.3.2. Если случайные векторы х и у имеют векторы математических ожиданий E(x)=x и Е(у)=y, то их ковариация
Применим эту теорему для нахождения матрицы ковариаций векторов х размеров 3х1 и у размеров 2х1
=E
=Е
=
=
E[(y–y)(y–y) T ]=
Дисперсии s11, s22, . sпп переменных y1, y2, . уп и их ковариации sij, для всех i≠j, могут быть удобно представлены матрицей дисперсий и ковариаций, которая иногда называется ковариационной матрицей и обозначается прописной буквой S строчной s:
S=D(у)= 
В матрице S i-я строка содержит дисперсию переменной уi и её ковариации с каждой из остальных переменных вектора у. Чтобы быть последовательными с обозначением sij, используем для дисперсий sii=si 2 , где i =1, 2, . n. При этом дисперсии расположены по диагонали матрицы S и ковариации занимают позиции за пределами диагонали. Отметим различие в значении между обозначениями D(у)=S для вектора и С(уi, уj)=sij для двух переменных.
Матрица S дисперсий и ковариаций симметричная, так как sij=sji [см. (3.2.9)]. Во многих приложениях полагается, что матрица S положительно определённая. Это обычно верно, если рассматриваются непрерывные случайные переменные, и между ними нет линейных зависимостей. Если между переменными есть линейные зависимости, то матрица S будет неотрицательно определённой.
Для примера найдём матрицу дисперсий и ковариаций вектора у размеров 3х1
=E
=E
=
=
Как следует из определения 3.3.3,
что после подобного сделанному в (3.2.4) преобразованию приводится к выражению
Последние два выражения являются естественным обобщением одномерных результатов данных выражениями (3.2.2) и (3.2.4).
Пример 3.3.1. Если а — какой-либо вектор числовых значений тех же размеров пх1, что и вектор у, то
Напомним, что симметричная матрица А является положительно определенной, если для всех векторов у≠0 квадратичная форма у Т Ау>0. В дальнейшем будет использоваться часто следующая теорема.
Теорема 3.3.3. Если у — вектор случайных переменных, в котором ни одна из переменных не является линейной комбинации остальных, то есть, нет вектора а≠0 и числа b таких, что а Т у=b для любого у, то D(у)=S — положительно определенная матрица.
Доказательство этой теоремы дано в [Себер (1980) стр.22].
Обобщенная дисперсия и нормированный вектор
Матрица S содержит дисперсии и ковариации всех п случайных переменных вектора у и всесторонне представляет полную их вариацию. Обобщённой мерой, характеризующей вариацию случайных переменных вектора у, может служить определитель матрицы S:
Обобщенная дисперсия =det(S). (3.3.9)
В качестве статистики обобщённой дисперсии используется обобщённая выборочная дисперсия, определяемая детерминантом матрицы S=Y T (I–Е/n)Y/(n–1) вариаций и ковариаций выборочных значений переменных вектора у, представленных матрицей Y=[y1, y2, …, yk], где её столбцы составлены из векторов значений переменных вектора у [Rencher, Christensen (2012) стр.81]:
Обобщенная выборочная дисперсия =det(S). (3.3.10)
Если det(S) малый, то значения переменных вектора у располагаются ближе к их усреднённым значениям вектора 
Для получения полезной меры разности между векторами у и y необходимо учитывать дисперсии и ковариации переменных вектора у. Как для одной нормированной случайной переменной, получаемой по формуле z=(у–y)/s и имеющей среднее равное 0 и дисперсию равную 1, нормированная разность между векторами у и y определяется в виде
Использование матрицы S –1 в этом выражении нормирует (трансформирует) переменные вектора у так, что нормированные переменные имеют средние равные 0 и дисперсии равные 1, а также становятся и некоррелированными. Это получается потому, что матрица S положительно определённая. По теореме П.6.5 её обратная матрица тоже положительно определённая. В силу (П.12.18), матрица S –1 =S –1/2 S –1/2 . Отсюда
где z=S –1/2 (у–y) — вектор нормированных случайных переменных. Математическое ожидание вектора z получается
и его дисперсия
Следовательно, по пункту 2 теоремы 4.5.2 следующей главы вектор S –1/2 (у–y) имеет нормальное распределение N(0, I).
Для нормированной разности, как параметра, есть соответствующая статистика, а именно, выборочная нормированная дистанция, определяемая формулой (у–






Видео:Ковариационная матрицаСкачать

Математическое ожидание и ковариационная матрица случайного вектора
В этом разделе рассмотрены числовые характеристики только двумерных случайных величин, поскольку обобщение на случай 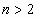
Пусть ( x , h ) — двумерная случайная величина, тогда M( x , h )=(M( x ), M( h )), т.е. математическое ожидание случайного вектора — это вектор из математических ожиданий компонент вектора.
Если ( x , h ) — дискретный случайный вектор с распределением
| y1 | y2 | . | ym | |
| x1 | p11 | p12 | . | p1m |
| x2 | p12 | p12 | . | p2m |
| . | . | . | pij | . |
| xn | pn1 | pn2 | . | pnm |
то математические ожидания компонент вычисляются по формулам:
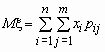
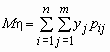
Эти формулы можно записать в сокращенном виде.
Обозначим 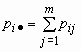
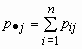
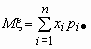
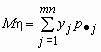
Если p( x , h )(x, y)- совместная плотность распределения непрерывной двумерной случайной величины ( x , h ), то
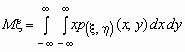
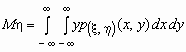
Поскольку 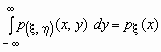
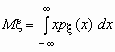
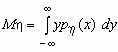
Понятие дисперсии обобщается на многомерные случайные величины нетривиальным образом. Это обобщение будет сделано в следующем разделе. Здесь лишь приведем формулы для вычисления дисперсии компонент двумерного случайного вектора.
Если ( x , h ) — двумерная случайная величина, то
D x = M( x — M x ) 2 = M x 2 — M( x ) 2 , D h = M( h — M h ) 2 = M h 2 — M( h ) 2 .
Входящие в эту формулу математические ожидания вычисляются по приведенным выше формулам.
Между случайными величинами может существовать функциональная зависимость. Например, если x — случайная величина и h = x 2 , то h — тоже случайная величина, связанная с x функциональной зависимостью. В то же время между случайными величинами может существовать зависимость другого рода, называемая стохастической. В разделе, посвященном условным распределениям уже обсуждалась такая зависимость. Из рассмотренных там примеров видно, что информация о значении одной случайной величины (одной компоненты случайного вектора) изменяет распределение другой случайной величины (другой компоненты случайного вектора), а это может, вообще говоря, изменить и числовые характеристики случайных величин.
Математическое ожидание, вычисленное по условному распределению, называется условным математическим ожиданием.
Для двумерного дискретного случайного вектора ( x , h ) с распределением
| y1 | y2 | . | ym | |
| x1 | p11 | p12 | . | p1m |
| x2 | p12 | p12 | . | p2m |
| . | . | . | pij | . |
| xn | pn1 | pn2 | . | pnm |
условное математическое ожидание случайной величины x при условии, что случайная величина h принимает значение yj, вычисляется по формуле 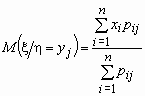
Аналогично, условное математическое ожидание случайной величины h при условии, что случайная величина x принимает значение xi, равно 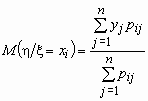
Видно, что условное математическое ожидание случайной величины x является функцией значений случайной величины h , т.е. M( x / h = y) = f1(y) и, совершенно аналогично, M( h / x = x) = f2(x).
Функцию f1(y) называют регрессией случайной величины x на случайную величину h , а f2(x) — регрессией случайной величины h на случайную величину x .
Если p( x , h )(x, y) совместная плотность вероятностей двумерной случайной величины ( x , h ), то
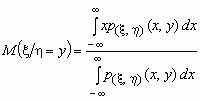
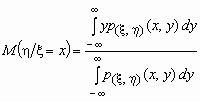
Если между случайными величинами x и h существует стохастическая связь, то одним из параметров, характеризующих меру этой связи является ковариация cov( x , h ). Ковариацию вычисляют по формулам cov( x , h )=M[( x — M x )( h — M h )] = M( x h ) — M x M h .
Если случайные величины x и h независимы, то cov( x , h )=0.
Обратное, вообще говоря, неверно. Из равенства нулю ковариации не следует независимость случайных величин. Случайные величины могут быть зависимыми в то время как их ковариация нулевая! Но зато, если ковариация случайных величин отлична от нуля, то между ними существует стохастическая связь, мерой которой и является величина ковариации.
cov( x , x ) = D x ;
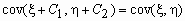
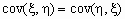
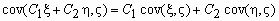
Ковариационной матрицей случайного вектора ( x , h ) называется матрица вида
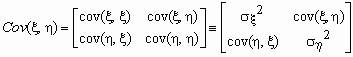
Эта матрица симметрична и положительно определена. Ее определитель называется обобщенной дисперсией и может служить мерой рассеяния системы случайных величин ( x , h ).
Как уже отмечалось ранее, дисперсия суммы независимых случайных величин равна сумме их дисперсий: 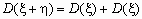
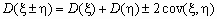
Понятно, что значение ковариации зависит не только от “тесноты” связи случайных величин, но и от самих значений этих величин, например, от единиц измерения этих значений. Для исключения этой зависимости вместо ковариации используется безразмерный коэффициент корреляции 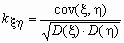
Этот коэффициент обладает следующими свойствами:
его модуль не превосходит единицы, т.е. 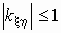
если x и h независимы, то k( x , h )=0 (обратное неверно!);
если 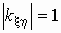
где a и b- некоторые числовые коэффициенты;
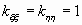
Корреляционной матрицей случайного вектора называется матрица
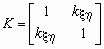
Если 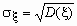
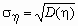
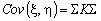
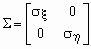
Исправляем ошибки: Нашли опечатку? Выделите ее мышкой и нажмите Ctrl+Enter
💥 Видео
Теория вероятностей #19: ковариация, корреляция, зависимость двух случайных величинСкачать

Корреляция и ковариация двумерной случайной величиныСкачать

Математическое ожидание дискретной случайной величины. 10 класс.Скачать

Математическое Ожидание, Дисперсия, Стандартное Отклонение за 5 минутСкачать

Случайный вектор двумерной случайной величиныСкачать

Математическое ожидание дискретной случайной величиныСкачать

Функция распределения дискретной случайной величиныСкачать

Теория вероятностей #12: случайная величина, плотность и функция распределенияСкачать

Теория вероятностей #25: Ковариация и корреляция / ковариационная матрицаСкачать

Теория вероятностей #14: математ. ожидание, дисперсия, медиана, мода, начальные моментыСкачать

Функция распределения непрерывной случайной величины. Вероятность попадания в интервалСкачать

Математическое ожидание и дисперсия непрерывной случайной величиныСкачать

Доказательство формулы для ковариационной матрицы у доски, линалСкачать

Функция распределения и плотность распределенияСкачать

ЧЕЛОВЕЧЕСТВО VS КАЗИНО. Покер. Математическое ожиданиеСкачать

Математическое ожидание и дисперсия. ТеорияСкачать

Свойства математического ожидания и дисперсииСкачать




























