Манхэттенская норма вектора это

Метрика ответственна за геометрию пространства. Геометрия это в первую очередь длины. По сути задание метрики сводится к заданию формулы вычисления длин. Сгенерируем несколько случайных точек на плоскости:

Расстояние от начала координат до точки можно найти из ее декартовых координат ( (x,y) ) по теореме Пифагора:

Данная формула и задает метрику Евклида. Она позволяет вычислять расстояния между точками. Любые геометрические фигуры есть просто множества точек. Вспомним школьное определение окружности: геометрическое место точек, удаленных на одинаковое расстояние от одной точки — центра окружности. Возьмем для простоты центр окружности в начале координат и будем рисовать только те случайные точки, которые оказались удаленными на примерно одно и то же расстояние от центра. Скажем, точки для которых расстояние от начала координат попало в небольшой интервал ( displaystyle 0.49 http://lightcone.ru/wp-content/uploads/2017/03/ice_video_20170323-110029.webm

Естественно мы получили окружность. Кажется, что других вариантов для вычисления расстояния быть не может. В рамках привычной нам Евклидовой геометрии это действительно так. Однако, было обнаружено, что существуют и другие геометрии. И они определяются заданием другой метрики. Переместим нашу окружность в Манхэттенскую геометрию, расстояния между точками в которой вычисляются по формуле:

( displaystyle d= |x|+|y| )

то есть просто сумма декартовых координат без учета их знака:

Это тоже окружность! Все точки равноудалены от центра. Просто расстояния в этой геометрии вычисляются чуть-чуть по другому. В программе поменялась всего одна строчка, вычисляющая ( displaystyle d ), то есть метрика.

Давайте еще раз перенесем нашу окружность в другой мир с другой геометрией. Будем вычислять расстояния с помощью метрики Чебышева:

( displaystyle d= max(|x|,|y|) )

то есть расстояние — это наибольшая из координат без учета знака.

По определению, это тоже окружность! Все точки равноудалены от центра. Окружность в пространстве Чебышева.

Видео:Зачем нужен ВЕКТОР. Объяснение смыслаСкачать

Евклидова, L1 и Чебышёва — 3 основные метрики, которые пригодятся в Data Science

Не важно, начинаете вы осваивать Data Science или работаете в этой сфере не первый год, вам наверняка пригодятся эти метрики. Разбираемся, что они из себя представляют и чем отличаются друг от друга.

Видео:Норма вектора. Часть 1.Скачать

Евклидово расстояние (расстояние по прямой)

Евклидово расстояние самое интуитивное для понимания: именно Евклидову метрику мы представляем, когда кто-то просит нас измерить расстояние между точками.

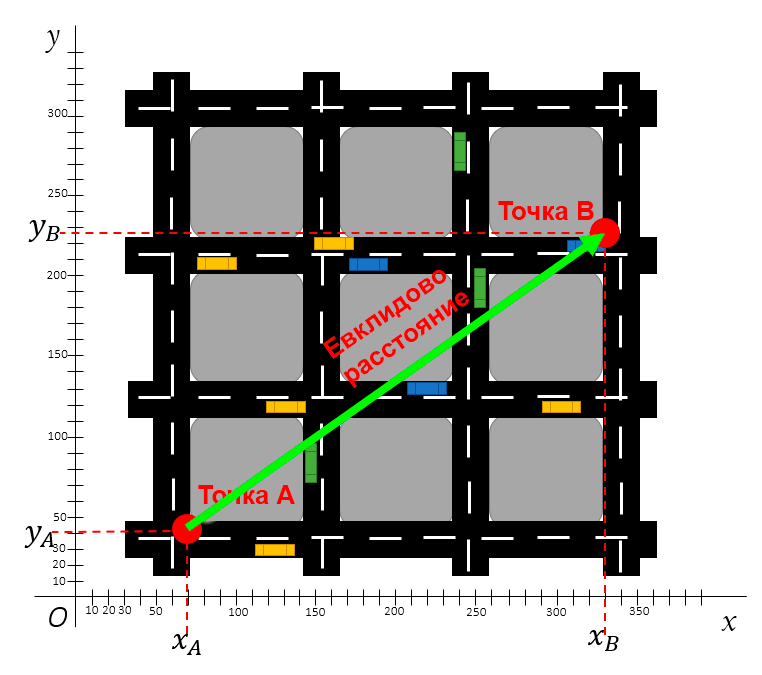
Евклидово расстояние — это прямая линия между двумя точками с координатами X и Y. Например, одной из таких точек может быть город на карте с его координатами долготы и широты.

Евклидово расстояние характеризуется прямой линией. Допустим, вам нужно измерить расстояние по прямой между точками A и B на карте города, приведённой ниже.

Евклидово расстояние между двумя точками считается по теореме Пифагора

Для расчёта Евклидового расстояния вам понадобятся лишь координаты этих двух точек. Дистанцию между ними можно будет рассчитать по формуле Пифагора.

Sportmaster Lab , Санкт-Петербург, Москва, Краснодар, можно удалённо , От 100 000 до 350 000 ₽

Теорема Пифагора гласит, что можно рассчитать длину «диагональной стороны» (гипотенузы) прямого треугольника, зная длины его горизонтальной и вертикальной стороны (катетов). Формула выглядит так: a² + b² = c².

Пример расчёта Евклидового расстояния

Прим. ред. В четвёртой строке вычислений допущена ошибка: (-260)^2 = 67 600, а не 76 600. Тогда результат будет равен

Видео:Что такое вектора? | Сущность Линейной Алгебры, глава 1Скачать

Расстояние L1 (расстояние городских кварталов)

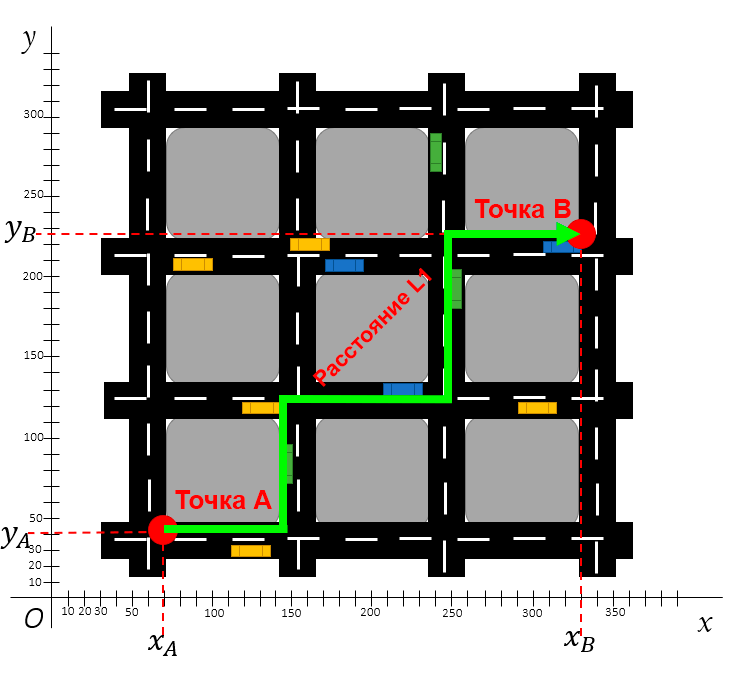
Расстояние L1 также известно как расстояние городских кварталов, манхэттенское расстояние, расстояние такси, метрика прямоугольного города — оно измеряет дистанцию не по кратчайшей прямой, а по блокам. Расстояние L1 измеряет дистанцию между городскими блоками: это расстояние всех прямых линий пути.

На следующем изображении показано расстояние L1 между двумя точками.

Расстояние L1 между двумя точками по блокам

Кроме показанного пути существует несколько альтернативных способов. Например, от точки A можно подняться на два блока вверх, а потом на три блока вправо, либо же на три блока вправо и два блока вверх.

Но расстояние L1 — это всё же просто дистанция, а поэтому траектория здесь не имеет значения. Единственное, что нужно понимать, это примерный путь: нужно пройти какое-то количество X блоков на восток и Y блоков на север. Сумма расстояний этих блоков и будет расстоянием L1 от точки A до точки B.

Пример расчёта расстояния L1 между двумя точками

Видео:Матрицы и векторыСкачать

Расстояние Чебышёва (метрика шахматной доски)

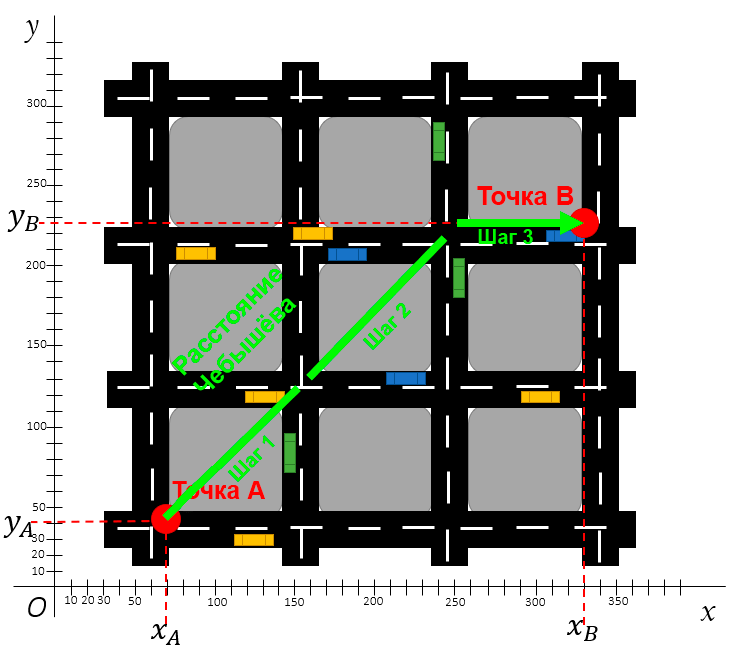
Расстояние Чебышёва известно ещё как расстояние шахматной доски. Чтобы понять принцип такой метрики, нужно представить короля на шахматной доске — он может ходить во всех направлениях: вперёд, назад, влево, вправо и по диагонали.

Расстояние Чебышёва между двумя точками

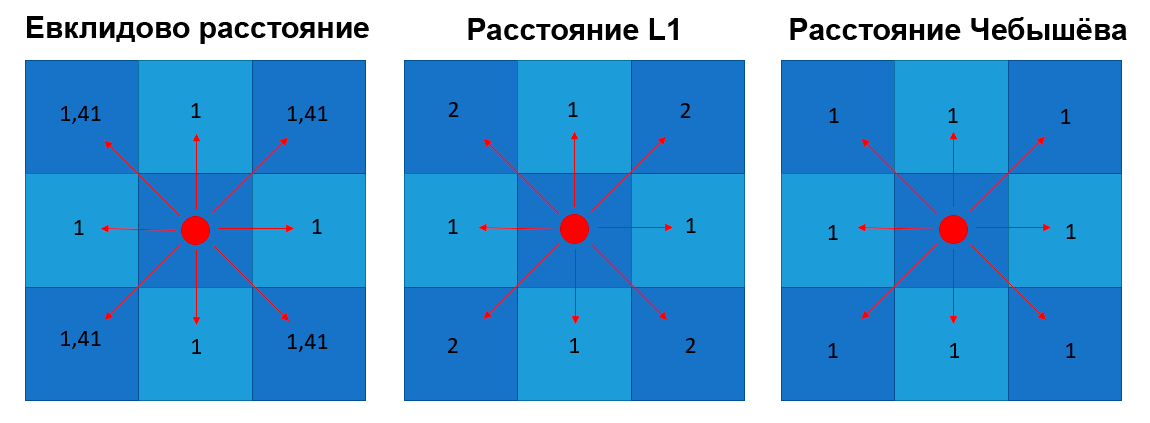
Разница расстояния L1 и расстояния Чебышёва в том, что при переходе на одну клетку по диагонали в первом случае засчитывается два хода (например вверх и влево), а во втором случае засчитывается всего один ход.

Ещё эти оба расстояния отличаются от Евклидового расстояния тем, что у Евклидового движение по диагонали рассчитывается по теореме Пифагора.

Сравнение путей 3 метрик

Расстояние Чебышёва можно представить как проход по шахматной доске.

Вот ещё один пример представления расстояния Чебышёва. Допустим, у вас есть дрон с двумя независимыми моторами: первый мотор тянет дрон вперёд, второй — в сторону. Оба мотора могут работать одновременно и равномерно на максимуме своей мощности.

Поэтому дрон может передвинуться на одну клетку по диагонали так же быстро, как по горизонтали или вертикали.

Посмотрите ещё раз на карту города по расстоянию Чебышёва. Первый шаг — оба мотора работают одновременно, второй шаг идентичен первому, а на третьем шаге мотор, тянущий дрон вперёд, отключается, и дрон смещается в сторону.

Таким образом, расстояние Чебышёва определяется как самая большая дистанция на одной оси.

Пример расчёта расстояния Чебышёва между двумя точками

Прим. ред. Полученный результат является условным и некорректно сравнивать его с другими результатами.

Видео:Лекция 2, Векторные и матричные нормы, унитарные матрицы, SVDСкачать

Важность дистанционных метрик в моделировании машинного обучения

Дата публикации Jan 13, 2019

Ряд алгоритмов машинного обучения — контролируемых или неконтролируемых — используют метрики расстояния, чтобы знать шаблон входных данных для принятия любого решения на основе данных. Хороший показатель расстояния помогает значительно повысить производительность процессов классификации, кластеризации и поиска информации. В этой статье мы обсудим различные метрики расстояния и то, как они помогают в моделировании машинного обучения.

Видео:Орт вектора. Нормировать вектор. Найти единичный векторСкачать

Введение

Во многих реальных приложениях мы используем алгоритмы машинного обучения для классификации или распознавания изображений, а также для извлечения информации из содержимого изображения. Например, распознавание лиц, цензурированные изображения в Интернете, розничный каталог, системы рекомендаций и т. Д. Здесь очень важно выбрать хороший показатель расстояния. Метрика расстояния помогает алгоритмам распознавать сходства между содержимым.

Определение базовой математики (Источник Википедия),

Метрика расстояния использует функцию расстояния, которая обеспечивает метрику отношения между каждым элементом в наборе данных.

Некоторые из вас могут подумать, что это за функция расстояния? как это работает? как он решает, что определенный контент или элемент данных имеет какие-либо отношения с другим? Что ж, давайте попробуем выяснить это в следующих нескольких разделах.

Видео:Норма вектора/Евклидово расстояние/Манхэттенская :Линейная алгебра для Data Science #datascienceСкачать

Функция расстояния

Вы помните изучение теоремы Пифагора? Если вы это сделаете, то вы можете вспомнить вычисление расстояния между двумя точками данных, используя теорему.

Чтобы вычислить расстояние между точками данных A и B, в теореме Пифагора рассматривается длина осей x и y.

Многим из вас должно быть интересно, используем ли мы эту теорему в алгоритме машинного обучения, чтобы найти расстояние? Чтобы ответить на ваш вопрос, да, мы используем его. Во многих алгоритмах машинного обучения мы используем приведенную выше формулу в качестве функции расстояния. Мы поговорим об алгоритмах, где он используется.

Теперь вы, наверное, поняли, что такое функция расстояния? Вот упрощенное определение.

Основное определение от Math.net,

Функция расстояния обеспечивает расстояние между элементами набора. Если расстояние равно нулю, то элементы эквивалентны, иначе они отличаются друг от друга.

Функция расстояния — это не что иное, как математическая формула, используемая метриками расстояния. Функция расстояния может отличаться в зависимости от метрики расстояния. Давайте поговорим о различных дистанционных метриках и поймем их роль в моделировании машинного обучения.

Видео:Лекция №2.2 НормыСкачать

Метрики расстояния

Существует несколько метрик расстояния, но для краткости этой статьи мы обсудим лишь несколько широко используемых метрик расстояния. Сначала мы попытаемся понять математику, стоящую за этими метриками, а затем определим алгоритмы машинного обучения, в которых мы используем эти метрики расстояния.

Ниже приведены часто используемые метрики расстояния —

Видео:Основы линейной алгебры. 4. Векторы. Часть 3Скачать

Минковский Расстояние:

Расстояние Минковского является метрикой в ​​нормированном векторном пространстве. Что такое нормированное векторное пространство? Нормированное векторное пространство — это векторное пространство, в котором определена норма. Предположим, что X — векторное пространство, тогда норма на X — вещественная функция ||Икс|| который удовлетворяет условиям ниже —

1. Нулевой вектор-Нулевой вектор будет иметь нулевую длину.
2. Скалярный фактор-Направление вектора не меняется, когда вы умножаете его на положительное число, хотя его длина будет изменена.
3. Неравенство треугольникаЕсли расстояние является нормой, то рассчитанное расстояние между двумя точками всегда будет прямой линией.

Вам может быть интересно, зачем нам нужен нормированный вектор, не можем ли мы просто перейти к простым метрикам? Поскольку нормированный вектор обладает указанными выше свойствами, это помогает поддерживать индуцированную норму метрико-однородной и трансляционной инвариантом. Более подробную информацию можно найтиВот,

Расстояние можно рассчитать по приведенной ниже формуле —

Расстояние Минковского является обобщенной метрикой расстояния. Здесь обобщенный означает, что мы можем манипулировать приведенной выше формулой, чтобы рассчитать расстояние между двумя точками данных различными способами.

Как уже упоминалось выше, мы можем манипулировать значениемпи рассчитать расстояние тремя разными способами-

р = 2, евклидово расстояние

р = ∞, расстояние чебычева

Мы обсудим эти метрики расстояния ниже подробно.

Манхэттен Расстояние:

Мы используем Манхэттенское расстояние, если нам нужно рассчитать расстояние между двумя точками данных в виде сетки, как путь. Как уже упоминалось выше, мы используемМинковское расстояниеформула, чтобы найти расстояние Манхэттена, установивр-хзначение как1,

Допустим, мы хотим рассчитать расстояние,dмежду двумя точками данныхИкса такжеY

Расстояниеdбудет рассчитываться с использованиемабсолютная сумма разностеймежду его декартовыми координатами, как показано ниже:

где, n- количество переменных,XIа такжеугявляются переменными векторов x и y соответственно в двумерном векторном пространстве. то естьх = (х1, х2, х3, . )а такжеу = (у1, у2, у3,…),

Теперь расстояниеdбудет рассчитываться как

(x1 — y1)+(x2 — y2)+(х3 — у3)+… +(xn — yn),

Если вы попытаетесь визуализировать расчет расстояния, он будет выглядеть примерно так:

Расстояние до Манхэттена также известно как геометрия такси, расстояние до городских кварталов и т.д.

Евклидово расстояние:

Евклидово расстояние — одна из наиболее часто используемых метрик расстояния. Он рассчитывается по формуле Минковского расстояния путем установкир-хзначение для2, Это обновит расстояние«D»формула как ниже:

Давай остановимся ненадолго! Эта формула выглядит знакомо? Ну да, мы только что видели эту формулу выше в этой статье при обсуждении«Теорема Пифагора».

Евклидова формула расстояния может быть использована для расчета расстояния между двумя точками данных на плоскости.

Видео:Линейная алгебра. Алексей Савватеев и Александр Тонис. Лекция 10.2. Норма линейного оператораСкачать

Расстояние косинуса:

В основном, метрика косинусного расстояния используется для поиска сходства между различными документами. В косинусной метрике мы измеряем степень угла между двумя документами / векторами (термин частоты в разных документах собирается как метрика). Эта конкретная метрика используется, когда величина между векторами не имеет значения, но ориентация.

Формула подобия косинуса может быть получена из уравнения точечных произведений:

Теперь вы должны подумать, какое значение угла косинуса будет полезно для определения сходства.

Теперь, когда у нас есть значения, которые будут рассматриваться для измерения сходства, нам нужно знать, что означают 1, 0 и -1.

Здесь значение косинуса 1 предназначено для векторов, указывающих в одном и том же направлении, то есть между документами / точками данных есть сходства. В нуле для ортогональных векторов, т. Е. Не связанных (найдено некоторое сходство). Значение -1 для векторов, указывающих в противоположных направлениях (без сходства).

Видео:Норма вектора. Часть 8.Скачать

Махаланобис Расстояние:

Расстояние Махаланобиса используется для расчета расстояния между двумя точками данных в многомерном пространстве.

Согласно определению Википедии,

Махаланобис расстояниеявляется мерой расстояния между точкой P и распределением D. Идея измерения состоит в том, сколько стандартных отклонений P от среднего значения D.

Преимущество использования расстояния по махаланобису заключается в том, что учитывается ковариация, которая помогает измерять силу / сходство между двумя различными объектами данных. Расстояние между наблюдением и средним может быть рассчитано, как показано ниже:

Здесь S — ковариационные метрики. Мы используем обратную метрику ковариации, чтобы получить нормализованное по дисперсии уравнение расстояния.

Теперь, когда у нас есть базовое представление о различных метриках расстояния, мы можем перейти к следующему шагу, а именно к методам / моделированию машинного обучения, в которых используются эти метрики различий.

Видео:Норма вектора. Часть 2.Скачать

Моделирование машинного обучения и дистанционные метрики

В этом разделе мы будем работать над некоторыми базовыми вариантами использования для классификации и кластеризации. Это поможет нам понять использование метрик расстояния в моделировании машинного обучения. Мы начнем с быстрого введения контролируемых и неконтролируемых алгоритмов и постепенно перейдем к примерам.

Видео:Что такое векторы и матрицы? Душкин объяснитСкачать

1. Классификация

K-Ближайшие соседи (KNN) —

KNN — это не вероятностный контролируемый алгоритм обучения, т.е. он не дает вероятности принадлежности к какой-либо точке данных, а KNN классифицирует данные при жестком назначении, например, точка данных будет принадлежать 0 или 1. Теперь вы должны подумать как работает KNN, если не используется уравнение вероятности. KNN использует метрики расстояния, чтобы найти сходства или различия.

Давайте возьмем набор данных iris, который имеет три класса, и посмотрим, как KNN будет определять классы для тестовых данных.

На изображении № 2 над черным квадратом находится тестовая точка данных. Теперь нам нужно найти, к какому классу относится эта контрольная точка данных, с помощью алгоритма KNN. Теперь мы подготовим набор данных для создания модели машинного обучения, чтобы предсказать класс для наших тестовых данных.

В алгоритме классификации КНН мы определяем постоянную«K».K — количество ближайших соседей контрольной точки данных. Эти K точек данных затем будут использоваться для определения класса для точки тестовых данных (обратите внимание, что это в наборе обучающих данных).

Вам интересно, как бы мы нашли ближайших соседей. Ну вот где метрика расстояния входит в картинки. Сначала мы рассчитываем расстояние между каждым поездом и контрольной точкой данных, а затем выбираем ближайшую вершину в соответствии со значением k.

Мы не будем создавать KNN с нуля, но будем использовать scikit KNN классификатор

Как видно из приведенного выше кода, мы используем метрику расстояния Минковского со значением p, равным 2, то есть в классификаторе KNN будет использоваться формула Евклидовой метрики расстояния.

По мере продвижения вперед в моделировании машинного обучения мы можем теперь обучать нашу модель и начинать предсказывать класс для тестовых данных.

Как только верхние ближайшие соседи выбраны, мы проверяем большинство проголосовавших классов в соседях —

Из приведенного выше изображения, вы можете угадать класс для контрольной точки? Это класс 1, так как он является самым популярным.

Из этого небольшого примера мы увидели, какметрика расстояниябыл важен для классификатора KNN.Это помогло нам получить самые близкие точки данных поезда, для которых были известны классы.Существует вероятность, что при использовании различных метрик расстояния мы могли бы получить лучшие результаты. Таким образом, в не вероятностном алгоритме, таком как KNN, метрики расстояния играют важную роль.

Видео:7 Какая система самая хорошая? Манхэттенская!Скачать

2. Кластеризация

K-нуждаемость

В алгоритмах классификации, вероятностных или не вероятностных, нам будут предоставлены помеченные данные, что упрощает прогнозирование классов. Хотя в алгоритме кластеризации у нас нет информации о том, какая точка данных принадлежит какому классу. Метрики расстояния являются важной частью этого вида алгоритма.

В K-средних мы выбираем количество центроидов, которые определяют количество кластеров.Затем каждая точка данных будет привязана к ближайшему центроиду, используя метрику расстояния (евклидово), Мы будем использовать данные радужной оболочки, чтобы понять основной процесс K-средних.

На приведенном выше изображении № 1, как вы можете видеть, мы случайно разместили центроиды, а на рисунке № 2, используя метрику расстояния, пытались найти ближайший класс кластеров.

Нам нужно будет повторять назначение центроидов до тех пор, пока у нас не будет четкой кластерной структуры.

Как мы видели в приведенном выше примере, не имея никаких знаний о метках с помощью метрики расстояния в K-средних, мы разбили данные на 3 класса.

Видео:Высшая математика. Линейные пространства. Векторы. БазисСкачать

3. Обработка естественного языка

Поиск информации

В поиске информации мы работаем с неструктурированными данными. Данные могут быть статьей, веб-сайтом, электронной почтой, текстовыми сообщениями, публикацией в социальных сетях и т. Д. С помощью методов, используемых в НЛП, мы можем создавать векторные данные таким образом, чтобы их можно было использовать для получения информации при запросе. Как только неструктурированные данные преобразуются в векторную форму, мы можем использовать метрику косинусного сходства, чтобы отфильтровать ненужные документы из корпуса.

Давайте возьмем пример и поймем использование косинусного сходства.

1. Создать векторную форму для Корпуса и Query-

2. Проверьте сходства, т.е. найдите, какой документ в корпусе имеет отношение к нашему запросу.

Как видно из приведенного выше примера, мы запросили слово«Коричневый»и в корпусе есть только три документа, которые содержат слово«Коричневый».При проверке с помощью косинусной метрики сходства он дал те же результаты, имея> 0 значений для трех документов, кроме четвертого

Видео:Норма вектора. Часть 4.Скачать

Вывод

В этой статье мы узнали о нескольких популярных метриках расстояния / сходства и о том, как их можно использовать для решения сложных задач машинного обучения. Надеюсь, что это будет полезно для людей, которые только начинают изучать машинное обучение и науку о данных.

📺 Видео

Коллинеарность векторовСкачать

Линейная алгебра для Data Science: Единичный вектор.Норма вектора. Внешнее произведение #datascienceСкачать

8 класс, 40 урок, Понятие вектораСкачать