Правильный восьмиугольник вписан в окружность найдите величину угла abc

В окружность вписан равносторонний восьмиугольник. Найдите величину угла ABC.

Решение:

Формула нахождения величины угла в правильном многоугольнике:
L=(180(n-2))/n
L — угол в многоугольнике.
n-количество сторон многоугольника.

Величина угла в восьмиугольнике равна:
n=8

∆ALB – равнобедренный т.к. AL=LB и углы LAB и LBA равны.
Найдем углы LAB и LBA из ∆ ALB:

Углы LAB= LBA=22,5
Угол LBA опирается на хорду LA.
LA сторона восьмиугольника, следовательно, LA=AC.
Углы LBA и ABC, т. к. опираются на равные хорды LA=AC

Подписывайтесь на канал на YOUTUBE и смотрите видео, подготавливайтесь к экзаменам по математике и геометрии с нами.

Видео:Геометрия: В окружность вписан равносторонний восьми угольник. Найдите величину угла АВС. / ЕГЭ ОГЭСкачать

В окружность вписан правильный восьмиугольник найдите угол

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

В окружность вписан равносторонний восьмиугольник. Найдите величину угла ABC.

В окружность вписан равносторонний восьмиугольник. Найдите величину угла ABC.

Решение:

Формула нахождения величины угла в правильном многоугольнике:
L=(180(n-2))/n
L — угол в многоугольнике.
n-количество сторон многоугольника.

Величина угла в восьмиугольнике равна:
n=8

∆ALB – равнобедренный т.к. AL=LB и углы LAB и LBA равны.
Найдем углы LAB и LBA из ∆ ALB:

Углы LAB= LBA=22,5
Угол LBA опирается на хорду LA.
LA сторона восьмиугольника, следовательно, LA=AC.
Углы LBA и ABC, т. к. опираются на равные хорды LA=AC

Подписывайтесь на канал на YOUTUBE и смотрите видео, подготавливайтесь к экзаменам по математике и геометрии с нами.

Видео:Видео урок Геометрия: В окружность вписан равносторонний восьмиугольник. Найдите величину угла АВС.Скачать

Свойство равностороннего восьмиугольника вписанного в окружность

Видео:ABCDEFGH — правильный восьмиугольник. Найдите угол EFG. Ответ дайте в градусах.Скачать

В окружность вписан равносторонний восьмиугольник. Найдите величину угла ABC.

В окружность вписан равносторонний восьмиугольник. Найдите величину угла ABC.

Решение:

Формула нахождения величины угла в правильном многоугольнике:
L=(180(n-2))/n
L — угол в многоугольнике.
n-количество сторон многоугольника.

Величина угла в восьмиугольнике равна:
n=8

∆ALB – равнобедренный т.к. AL=LB и углы LAB и LBA равны.
Найдем углы LAB и LBA из ∆ ALB:

Углы LAB= LBA=22,5
Угол LBA опирается на хорду LA.
LA сторона восьмиугольника, следовательно, LA=AC.
Углы LBA и ABC, т. к. опираются на равные хорды LA=AC

Подписывайтесь на канал на YOUTUBE и смотрите видео, подготавливайтесь к экзаменам по математике и геометрии с нами.

Видео:В угол C величиной 83° вписана окружность ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать

Правильный многоугольник

Видео:Углы, вписанные в окружность. 9 класс.Скачать

Формулы, признаки и свойства правильного многоугольника

Многоугольником называется часть площади, которая ограничена замкнутой ломаной линией, не пересекающей сама себя.

Многоугольники отличаются между собой количеством сторон и углов.

Правильный многоугольник — это многоугольник, у которого все стороны и углы одинаковые.

Признаки правильного многоугольника

Многоугольник будет правильным, если выполняется следующее условие: все стороны и углы одинаковы.

a 1 = a 2 = a 3 = … = a n-1 = a n ,

α 1 = α 2 = α 3 = … = α n-1 = α n

где a₁ … a_n — длины сторон правильного многоугольника,
α ₁ … α _n — внутренние углы между стронами правильного многоугольника.

Основные свойства правильного многоугольника

1. Все стороны равны: a 1 = a 2 = a 3 = … = a n-1 = a n
2. Все углы равны: α 1 = α 2 = α 3 = … = α n-1 = α n
3. Центр вписанной окружности O_в совпадает с центром описанной окружности O_о, что и образуют центр многоугольникаO.
4. Сумма всех углов n-угольника равна: 180° · n — 2
5. Сумма всех внешних углов n-угольника равна 360°: β 1 + β 2 + β 3 + … + β n-1 + β n = 360°
6. Количество диагоналей (D_n) n-угольника равна половине произведения количества вершин на количество диагоналей, выходящих из каждой вершины: D n = n · n — 3 2
7. В любой многоугольник можно вписать окружность и описать круг; при этом площадь кольца, образованная этими окружностями, зависит только от длины стороны многоугольника: S = π 4 · a 2
8. Все биссектрисы углов между сторонами равны и проходят через центр правильного многоугольника O .

Видео:Четырёхугольник ABCD вписан в окружность ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать

Формулы правильного n-угольника

Формулы длины стороны правильного n-угольника

Формула стороны правильного n-угольника через радиус вписанной окружности

a = 2 · r · tg 180° n (через градусы),

a = 2 · r · tg π n (через радианы)

Формула стороны правильного n-угольника через радиус описанной окружности

a = 2 · R · sin 180° n (через градусы),

a = 2 · R · sin π n (через радианы)

Формулы радиуса вписанной окружности правильного n-угольника

Формула радиуса вписанной окружности n-угольника через длину стороны

r = a : 2 · tg 180° n (через градусы),

r = a : 2 · tg π n (через радианы)

Формула радиуса описанной окружности правильного n-угольника

Формула радиуса описанной окружности n-угольника через длину стороны

R = a : 2 · sin 180° n (через градусы),

R = a : 2 · sin π n (через радианы)

Формулы площади правильного n-угольника

Формула площади n-угольника через длину стороны

Формула площади n-угольника через радиус вписанной окружности

Формула площади n-угольника через радиус описанной окружности

Формула периметра правильного многоугольника

Формула периметра правильного n-угольника

Периметр правильного n-угольника равен произведению длины одной стороны правильного n-угольника на количество его сторон.

Формула определения угла между сторонами правильного многоугольника

Формула угла между сторонами правильного n-угольника

Видео:ОГЭ 2020 задание 17Скачать

Правильный треугольник

Правильный треугольник — это правильный многоугольник с тремя сторонами. Все стороны правильного треугольника равны между собой, все углы также равны и составляют 60°.

Формулы правильного треугольника

Формула стороны правильного треугольника через радиус вписанной окружности

Сторона правильного треугольника равна удвоенному произведению радиуса вписанной окружности на корень из трёх.

Формула стороны правильного треугольника через радиус описанной окружности

Сторона правильного треугольника равна произведению радиуса описанной окружности на корень из трёх.

Формула площади правильного треугольника через длину стороны

Формула площади правильного треугольника через радиус вписанной окружности

Формула площади правильного треугольника через радиус описанной окружности

Углы между сторонами правильного треугольника

Видео:Задача 6 №27862 ЕГЭ по математике. Урок 105Скачать

Правильный четырехугольник

Правильный четырехугольник — это квадрат.

Формулы правильного четырехугольника

Формула стороны правильного четырехугольника через радиус вписанной окружности

Сторона правильного четырехугольника равна двум радиусам вписанной окружности.

Формула стороны правильного четырехугольника через радиус описанной окружности

Сторона правильного четырехугольника равна произведению радиуса описанной окружности на корень из двух.

Формула радиуса вписанной окружности правильного четырехугольника через длину стороны

Радиус вписанной окружности правильного четырехугольника равен половине стороны четырехугольника.

Формула радиуса описанной окружности правильного четырехугольника через длину стороны

Радиус описанной окружности правильного четырехугольника равен половине произведения стороны четырехугольника на корень из двух.

Формула площади правильного четырехугольника через длину стороны

Площадь правильного четырехугольника равна квадрату стороны четырехугольника.

Формула площади правильного четырехугольника через радиус вписанной окружности

Площадь правильного четырехугольника равна четырем радиусам вписанной окружности четырехугольника.

Формула площади правильного четырехугольника через радиус описанной окружности

Площадь правильного четырехугольника равна двум квадратам радиуса описанной окружности.

Углы между сторонами правильного четырехугольника

Видео:4K Как построить восьмиугольник по заданной стороне, octagon constructing with using a compassСкачать

Правильный шестиугольник

Правильный шестиугольник — это правильный многоугольник с тремя сторонами. Все стороны правильного шестиугольника равны между собой, все углы также равны и составляют 120°.

Формулы правильного шестиугольник

Формула стороны правильного шестиугольника через радиус вписанной окружности

Формула стороны правильного шестиугольника через радиус описанной окружности

Длина стороны правильного шестиугольника равна радиусу описанной окружности.

Формула радиуса вписанной окружности правильного шестиугольника через длину стороны

Формула радиуса описанной окружности правильного шестиугольника через длину стороны

Формула площади правильного шестиугольника через длину стороны

Формула площади правильного шестиугольника через радиус вписанной окружности

Формула площади правильного шестиугольника через радиус описанной окружности

Углы между сторонами правильного шестиугольника

Видео:Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

Правильный восьмиугольник

Правильный восьмиугольник — это правильный многоугольник с тремя сторонами. Все стороны правильного восьмиугольник равны между собой, все углы также равны и составляют 135°.

Видео:№702. В окружность вписан треугольник ABC так, что АВ — диаметр окружности. Найдите углыСкачать

Как найти сумму углов правильного восьмиугольника? Геометрия

Содержание:

Многоугольником называется геометрическая фигура, ограниченная ломаной или контуром. Последний состоит минимум из трёх отрезков. Точки, где ломаная изменяет угол, называются вершинами геометрической фигуры, каждое из таких звеньев – сторонами. Подробнее ознакомимся с равносторонним многоугольником – октагоном: его свойствами, особенностями; рассмотрим, как вычислить сумму его внутренних углов.

Видео:ОГЭ математика ОКРУЖНОСТИ 17#1🔴Скачать

Особенности и свойства

Различают два типа многоугольников:

• простые – ломаная, которая ограничивает фигуру, не пересекает сама себя;
• сложные – она имеет точки пересечения.

К первым относят прямоугольники, треугольники, ко вторым – звёздчатые геометрические тела, например, звёзды с соединёнными вершинами.

Выпуклой называют фигуру, лежащую в одной полуплоскости относительно её сторон. К выпуклым относятся n-угольники, с равной длиной всех сторон и внутренними углами.

N-угольник может быть:

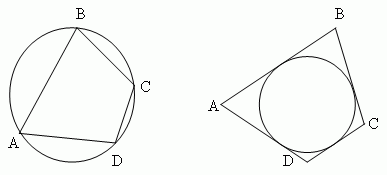
• вписанным – вершины принадлежат одному кругу;
• описанным вокруг неё, когда его стороны касаются одной окружности.

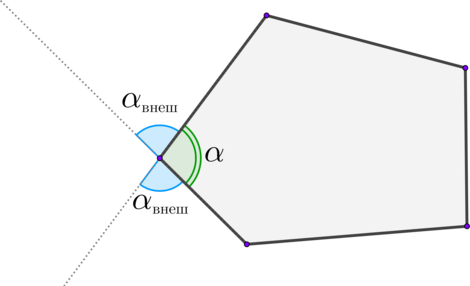
Углы, образованные соседними сторонами или звеньями, называются внутренними (a), смежные с ними – наружными или внешними (a_внеш).

У правильного многоугольника все стороны и углы равны, независимо от их числа.

Видео:ABCDEFGHI – правильный девятиугольник ... | ОГЭ 2017 | ЗАДАНИЕ 11 | ШКОЛА ПИФАГОРАСкачать

Как найти сумму углов правильного восьмиугольника

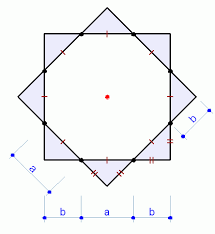
Октагон может образоваться путём квазиправильного усечения квадрата или наложением двух одинаковых квадратов с поворотом одного на 45° относительно общего центра.

Правило вычисления действует для любого правильного n-угольника. Вычисления проводятся по формуле: 180 * (n — 2), где n – количество углов геометрической фигуры.

Видео:Задача 6 №27916 ЕГЭ по математике. Урок 133Скачать

Пример

Зная описанное выше правило 180 * (n — 2), приступаем к вычислениям. Вместо n подставляем значение – восьмёрку, так как имеем правильный октагон.

Получим: 180 * (8 — 2) = 180 * 6 = 1080°.

Внутренний угол равен: 1080° : 8 = 135°.

Ответ: сумма углов правильного восьмиугольника равна 1080°.

📹 Видео

Равносторонний треугольник вписан в окружность. Найти площадь меньшего сегмента.Скачать

Четырехугольники, вписанные в окружность. 9 класс.Скачать

Нахождение угла восьмиугольника, вписанного в окружностьСкачать

Геометрия - Построение восьмиугольникаСкачать

Задача 6 №27859 ЕГЭ по математике. Урок 104Скачать