Контрольная работа по теме координаты и векторы 1 вариант

Даны четыре варианта контрольной работы, удобно вносить изменения и печатать.

Просмотр содержимого документа
«Контрольная работа № 1 по теме «Координаты и векторы в пространстве» (11 класс, Мерзляк А.Г. и др.)»

Контрольная работа № 1 по теме «Координаты и векторы в пространстве»

1. Точка A — середина отрезка MK. Найдите координаты точки A и длину отрезка MK, если M (5; −2; 1), K (3; 4; −3).

2. Точки A и B симметричны относительно точки C. Найдите координаты точки B, если A (−3; 5; −7), C (6; 2; −1).

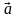
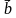
3. Даны векторы (3; −2; −1) и (1; 2; 4). Найдите:

1) координаты вектора ;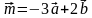

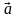
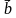
2) косинус угла между векторами и .

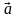
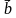
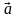
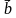
4. Даны векторы (2; −6; 8) и (−1; k; −4). При каком значении k векторы и :

5. Составьте уравнение плоскости, проходящей через точку A и перпендикулярной прямой AB, если A (1; 2; −3), B (4; 8; −6).

6. Дан куб ABCDA₁B₁C₁D₁, ребро которого равно 1 см. На диагонали C₁D его грани отметили точку M так, что DM : MC₁ = 5 : 3.

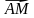
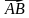
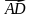
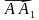
1) Выразите вектор через векторы , и .

2) Найдите модуль вектора .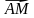

1. Точка M — середина отрезка AB. Найдите координаты точки M и длину отрезка AB, если A (6; −5; 2), B (−4; 3; 10).

2. Точки M и K симметричны относительно точки D. Найдите координаты точки K, если M (4; −6; 3), D (−2; 1; 5).

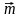
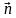
3. Даны векторы (2; −1; 3) и (−1; 2; 5). Найдите:

1) координаты вектора ;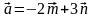

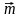
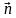
2) косинус угла между векторами и .

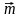
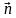
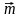
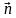
4. Даны векторы (5; −4; 6) и (15; −12; p). При каком значении p векторы и :

5. Составьте уравнение плоскости, проходящей через точку B и перпендикулярной прямой BC, если B (3; −2; 4), C (−2; 8; 19).

6. Дан куб ABCDA₁B₁C₁D₁, ребро которого равно 1 см. На диагонали AD₁ его грани отметили точку E так, что AE : ED₁ = 2 : 7.

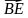
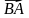
1) Выразите вектор через векторы , и .

2) Найдите модуль вектора .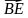

1. Точка K — середина отрезка CD. Найдите координаты точки K и длину отрезка CD, если C (−3; 4; −1), D (1; −2; 3).

2. Точки E и F симметричны относительно точки P. Найдите координаты точки F, если E (0; −8; 4), P (−4; 2; 2).

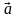
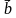
3. Даны векторы (2; 0; −3) и (1; −2; −1). Найдите:

1) координаты вектора ;

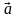
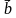
2) косинус угла между векторами и .

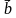
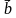
4. Даны векторы (−20; 10; −15) и (a; −2; 3). При каком значении a векторы и :

5. Составьте уравнение плоскости, проходящей через точку C и перпендикулярной прямой CD, если C (4; 1; −1), D (7; −2; 5).

6. Дан куб ABCDA₁B₁C₁D₁, ребро которого равно 1 см. На диагонали A₁B его грани отметили точку K так, что A₁K : KB = 4 : 3.

1) Выразите вектор через векторы , и .

2) Найдите модуль вектора .

1. Точка D — середина отрезка FK. Найдите координаты точки D и длину отрезка FK, если F (6; −3; 2), K (4; 1; 4).

2. Точки B и C симметричны относительно точки M. Найдите координаты точки B, если C (9; −5; 6), M (3; 0; −2).

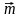
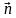
3. Даны векторы (4; −1; 2) и (−2; 1; 0). Найдите:

1) координаты вектора ;

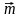
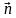
2) косинус угла между векторами и .

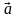
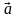
4. Даны векторы (1; −2; 3) и (7; m; 21). При каком значении m векторы и :

5. Составьте уравнение плоскости, проходящей через точку D и перпендикулярной прямой DM, если D (−3; 20; −4), M (9; 24; 16).

6. Дан куб ABCDA₁B₁C₁D₁, ребро которого равно 1 см. На диагонали AC его грани отметили точку F так, что AF : FC = 3 : 7.

Видео:РАЗБОР КОНТРОЛЬНОЙ РАБОТЫ | 9 КЛАСС ГЕОМЕТРИЯ АТАНАСЯН | ВЕКТОРЫСкачать

Контрольная работа по теме: «Координаты и векторы в пространстве», 11 класс, геометрия

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Видео:11 класс. Контрольная №1 (из 6). Тема: Координаты точки и координаты вектора. В конце 2-ой вариант!Скачать

Коммуникативный педагогический тренинг: способы взаимодействия с разными категориями учащихся

Сертификат и скидка на обучение каждому участнику

Контрольная работа по теме:

«Координаты и векторы в пространстве»

Даны точки: А(-3; 2; -4) и В(5; -4; 6). Найдите

длину отрезка АВ;

координаты середины отрезка АВ;

Даны точки: А(-2; 5; -6), В(7; -5; 1) и С(3; -7; 4). Найдите

координаты векторов и ;

модуль вектора ;

косинус угла между векторами и .

Определите, при каком значении переменной х

вектора ( х ; -4; 3) и (-15; 12; -9) а) перпендикулярны; б) коллинеарны?

Укажите вектор параллельного переноса, при котором точка А(2; -4; 5) переходит в точку В, симметричную точке А относительно плоскости (Ох z ). Запишите формулы этого параллельного переноса.

Контрольная работа по теме:

«Координаты и векторы в пространстве»

Даны точки: А(3; -2; -3) и В(-5; 4; -9). Найдите

длину отрезка АВ;

координаты середины отрезка АВ;

Даны точки: F (2; -3; 0), G (7; -5; -4) и N (-3; -1; -4). Найдите

координаты векторов и ;

модуль вектора ;

координаты вектора ;

косинус угла между векторами и .

Определите, при каком значении переменной х

вектора (2; -1; 8) и (-10; х ; -40) а) перпендикулярны; б) коллинеарны?

Укажите вектор параллельного переноса, при котором точка А(-2; 4; -8) переходит в точку В, симметричную точке А относительно плоскости (Оху). Запишите формулы этого параллельного переноса.

11_гео Контрольная работа по теме:

«Координаты и векторы в пространстве»

Даны точки: М(-2; -3; -4) и В(6; -9; 0). Найдите

длину отрезка МВ;

координаты середины отрезка МВ;

Даны точки: А(-2; -5; -6), В(-7; -5; 1) и С(3; -7; -4). Найдите

координаты векторов и ;

модуль вектора ;

координаты и длину вектора

косинус угла между векторами и

Определите, при каком значении переменной у

вектора (5; -4; 3) и (-15; 12; у ) а) перпендикулярны; б) коллинеарны?

Укажите вектор параллельного переноса, при котором точка А(-5; 8; 1) переходит в точку В, симметричную точке А относительно плоскости (Оу z ). Запишите формулы этого параллельного переноса.

11_гео Контрольная работа по теме:

«Координаты и векторы в пространстве»

Даны точки: А(3; -2; -3) и В(-5; 4; -9). Найдите

длину отрезка АВ;

координаты середины отрезка АВ;

Даны точки: F (-1; -3; 0), G (0; -5; -4) и N (-3; -1; -4). Найдите

координаты векторов и ;

модуль вектора ;

координаты и длину вектора ;

косинус угла между векторами и .

Определите, при каком значении переменной у

вектора ( у ; -1; 8) и (10; -5; 40) а) перпендикулярны; б) коллинеарны?

Укажите вектор параллельного переноса, при котором точка А(6; -4; 3) переходит в точку В, симметричную точке А относительно плоскости (Оху). Запишите формулы этого параллельного переноса.

Контрольная работа по теме:

«Координаты и векторы в пространстве»

Даны точки: А(-3; 2; -4) и В(5; -4; 6). Найдите

длину отрезка АВ;

координаты середины отрезка АВ;

Даны точки: А(-2; 5; -6), В(7; -5; 1) и С(3; -7; 4). Найдите

координаты векторов и ;

модуль вектора ;

косинус угла между векторами и .

Определите, при каком значении переменной х

вектора ( х ; -4; 3) и (-15; 12; -9) а) перпендикулярны; б) коллинеарны?

Укажите вектор параллельного переноса, при котором точка А(2; -4; 5) переходит в точку В, симметричную точке А относительно плоскости (Ох z ). Запишите формулы этого параллельного переноса.

Контрольная работа по теме:

«Координаты и векторы в пространстве»

Даны точки: А(3; -2; -3) и В(-5; 4; -9). Найдите

длину отрезка АВ;

координаты середины отрезка АВ;

Даны точки: F (2; -3; 0), G (7; -5; -4) и N (-3; -1; -4). Найдите

координаты векторов и ;

модуль вектора ;

координаты вектора ;

косинус угла между векторами и .

Определите, при каком значении переменной х

вектора (2; -1; 8) и (-10; х ; -40) а) перпендикулярны; б) коллинеарны?

Укажите вектор параллельного переноса, при котором точка А(-2; 4; -8) переходит в точку В, симметричную точке А относительно плоскости (Оху). Запишите формулы этого параллельного переноса.

Контрольная работа по теме:

«Координаты и векторы в пространстве»

Даны точки: М(-2; -3; -4) и В(6; -9; 0). Найдите

длину отрезка МВ;

координаты середины отрезка МВ;

Даны точки: А(-2; -5; -6), В(-7; -5; 1) и С(3; -7; -4). Найдите

координаты векторов и ;

модуль вектора ;

косинус угла между векторами и

Определите, при каком значении переменной у

вектора (5; -4; 3) и (-15; 12; у ) а) перпендикулярны; б) коллинеарны?

Укажите вектор параллельного переноса, при котором точка А(-5; 8; 1) переходит в точку В, симметричную точке А относительно плоскости (Оу z ). Запишите формулы этого параллельного переноса.

Контрольная работа по теме:

«Координаты и векторы в пространстве»

Даны точки: А(3; -2; -3) и В(-5; 4; -9). Найдите

длину отрезка АВ;

координаты середины отрезка АВ;

Даны точки: F (-1; -3; 0), G (0; -5; -4) и N (-3; -1; -4). Найдите

координаты векторов и ;

модуль вектора ;

координаты вектора ;

косинус угла между векторами и .

Определите, при каком значении переменной у

вектора ( у ; -1; 8) и (10; -5; 40) а) перпендикулярны; б) коллинеарны?

Укажите вектор параллельного переноса, при котором точка А(6; -4; 3) переходит в точку В, симметричную точке А относительно плоскости (Оху). Запишите формулы этого параллельного переноса.

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 945 человек из 80 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 679 человек из 75 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 302 человека из 66 регионов

Ищем педагогов в команду «Инфоурок»

Видео:Подготовка к контрольной работе Координаты и векторыСкачать

Дистанционные курсы для педагогов

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 507 161 материал в базе

Другие материалы

• 26.02.2017
• 7324
• 243

• 26.02.2017
• 371
• 0

• 26.02.2017
• 864
• 18

• 26.02.2017
• 335
• 0

• 26.02.2017
• 856
• 1

• 26.02.2017
• 782
• 0

• 26.02.2017
• 1774
• 11

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Добавить в избранное

• 26.02.2017 35504
• DOCX 84.8 кбайт
• 324 скачивания
• Рейтинг: 3 из 5
• Оцените материал:

Настоящий материал опубликован пользователем Топоровская Татьяна Валентиновна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

• На сайте: 7 лет
• Подписчики: 23
• Всего просмотров: 360650
• Всего материалов: 30

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Видео:ВЕКТОРЫ. Контрольная № 4 Геометрия 9 класс.Скачать

Дистанционные курсы
для педагогов

663 курса от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Минпросвещения намерено решить вопрос с третьей сменой в школах в 2023 году

Время чтения: 1 минута

Школы Пскова перевели на дистанционное обучение

Время чтения: 2 минуты

Школьники Чебоксар с 27 января перейдут на дистанционный формат обучения

Время чтения: 1 минута

Большинство российских вузов используют смешанный формат обучения

Время чтения: 1 минута

В Роспотребнадзоре заявили о широком распространении COVID-19 среди детей

Время чтения: 1 минута

В школьном курсе мировой истории планируют уделить больше внимания Азии и Африке

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Видео:9 класс. Контрольная №1 (из 6). Тема: Векторы. Подробное решение с объяснением. Пробуем свои силы!Скачать

Контрольная работа по теме «Векторы» для СПО по математике

Контрольная работа по теме «Координаты и векторы»

А. Теоретическая часть

1. Дайте определение понятия «вектор».

2. Как вычислить координаты вектора?

3. Как вычислить длину вектора?

4. Какие векторы называются равными?

5. Что такое «коллинеарные векторы». Укажите условия коллинеарности.

6. Какие векторы называются компланарными?

7. Какие векторы называются ортогональными?

8. Скалярное произведение векторов. Понятие и формулы.

9. Условие ортогональности векторов.

В. Практическая часть.

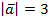
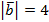
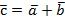
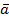
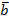
1. Длина вектора , . Вектор . Найдите длину вектора , изобразите на рисунке сложение векторов и , если угол между ними составляет 90 0 .

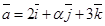
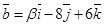
2. При каком значении a и b векторы и коллинеарны?

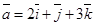
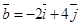
3. Являются ли векторы и ортогональными?

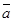
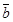
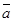
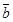
4. Векторы и образуют угол 120°. │ │= 8, │ │= 2. Вычислить скалярное произведение векторов этих векторов.

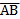
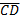
5. Даны точки А(2;1;4), В(3;5;7), С(3;-1;2), D (4;2;1). Найти скалярное произведение векторов и .

Контрольная работа по теме «Координаты и векторы»

А. Теоретическая часть

1. Дайте определение понятия «вектор».

2. Как вычислить координаты вектора?

3. Как вычислить длину вектора?

4. Какие векторы называются равными?

5. Что такое «коллинеарные векторы». Укажите условия коллинеарности.

6. Какие векторы называются компланарными?

7. Какие векторы называются ортогональными?

8. Скалярное произведение векторов. Понятие и формулы.

9. Условие ортогональности векторов.

В. Практическая часть.

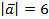
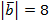
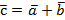
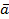
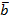
1. Длина вектора , . Вектор . Найдите длину вектора , изобразите на рисунке сложение векторов и , если угол между ними составляет 90 0 .

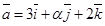
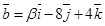
2. При каком значении a и b векторы и коллинеарны?

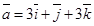
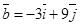
3. Являются ли векторы и ортогональными?

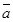
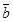
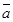
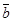
4. Векторы и образуют угол 120°. │ │= 7, │ │= 5. Вычислить скалярное произведение этих векторов.

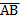
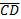
5. Даны точки А(4;3;2), В(7;-1;5), С(2;-3;7), D (1;3;-5). Найти скалярное произведение векторов и .

🎦 Видео

Векторы. Метод координат. Вебинар | МатематикаСкачать

Контрольная работа по геометрии по теме "Метод координат". Разбор заданий. Геометрия 9 классСкачать

9 кл Геометрия КР№1 ВекторыСкачать

Координаты вектора. 9 класс.Скачать

ВЕКТОРЫ 9 класс С НУЛЯ | Математика ОГЭ 2023 | УмскулСкачать

Координаты вектора в пространстве. 11 класс.Скачать

Геометрия 9. Подготовка к КР по теме ВекторыСкачать

Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Координаты точки и координаты вектора 1.Скачать

Нахождение длины вектора через координаты. Практическая часть. 9 класс.Скачать

РАЗБОР КОНТРОЛЬНОЙ РАБОТЫ | АТАНАСЯН 9 КЛАСС | МЕТОД КООРДИНАТСкачать

Нахождение координат вектора. Практическая часть. 9 класс.Скачать

9 класс, 2 урок, Координаты вектораСкачать

9 класс. КР№2. Метод координат. Задание №1Скачать