Линейные и нелинейные векторы

В данной статье мы расскажем:

• что такое коллинеарные векторы;
• какие существуют условия коллинеарности векторов;
• какие существуют свойства коллинеарных векторов;
• что такое линейная зависимость коллинеарных векторов.

Видео:Линейная алгебра. Векторы и операции над векторами.Скачать

Коллинеарные векторы

Коллинеарные векторы — это векторы, которые являются параллелями одной прямой или лежат на одной прямой.

Видео:Линейная зависимость векторов на примерахСкачать

Условия коллинеарности векторов

Два векторы являются коллинеарными, если выполняется любое из следующих условий:

• условие 1. Векторы a и b коллинеарны при наличии такого числа λ , что a = λ b ;
• условие 2. Векторы a и b коллинеарны при равном отношении координат:

a = ( a 1 ; a 2 ) , b = ( b 1 ; b 2 ) ⇒ a ∥ b ⇔ a 1 b 1 = a 2 b 2

• условие 3. Векторы a и b коллинеарны при условии равенства векторного произведения и нулевого вектора:

Условие 2 неприменимо, если одна из координат вектора равна нулю.

Условие 3 применимо только к тем векторам, которые заданы в пространстве.

Видео:Линейная зависимость и линейная независимость векторов.Скачать

Примеры задач на исследование коллинеарности векторов

Исследуем векторы а = ( 1 ; 3 ) и b = ( 2 ; 1 ) на коллинеарность.

В данном случае необходимо воспользоваться 2-м условием коллинеарности. Для заданных векторов оно выглядит так:

Равенство неверное. Отсюда можно сделать вывод, что векторы a и b неколлинеарны.

Ответ: a | | b

Какое значение m вектора a = ( 1 ; 2 ) и b = ( — 1 ; m ) необходимо для коллинеарности векторов?

Используя второе условие коллинераности, векторы будут коллинеарными, если их координаты будут пропорциональными:

Отсюда видно, что m = — 2 .

Ответ: m = — 2 .

Видео:Линейная зависимость векторовСкачать

Критерии линейной зависимости и линейной независимости систем векторов

Система векторов векторного пространства линейно зависима только в том случае, когда один из векторов системы можно выразить через остальные векторы данной системы.

Пусть система e 1 , e 2 , . . . , e n является линейно зависимой. Запишем линейную комбинацию этой системы равную нулевому вектору:

a 1 e 1 + a 2 e 2 + . . . + a n e n = 0

в которой хотя бы один из коэффициентов комбинации не равен нулю.

Пусть a k ≠ 0 k ∈ 1 , 2 , . . . , n .

Делим обе части равенства на ненулевой коэффициент:

a k — 1 ( a k — 1 a 1 ) e 1 + ( a k — 1 a k ) e k + . . . + ( a k — 1 a n ) e n = 0

— a k — 1 a m , где m ∈ 1 , 2 , . . . , k — 1 , k + 1 , n

β 1 e 1 + . . . + β k — 1 e k — 1 + β k + 1 e k + 1 + . . . + β n e n = 0

или e k = ( — β 1 ) e 1 + . . . + ( — β k — 1 ) e k — 1 + ( — β k + 1 ) e k + 1 + . . . + ( — β n ) e n

Отсюда следует, что один из векторов системы выражается через все остальные векторы системы. Что и требовалось доказать (ч.т.д.).

Пусть один из векторов можно линейно выразить через все остальные векторы системы:

e k = γ 1 e 1 + . . . + γ k — 1 e k — 1 + γ k + 1 e k + 1 + . . . + γ n e n

Переносим вектор e k в правую часть этого равенства:

0 = γ 1 e 1 + . . . + γ k — 1 e k — 1 — e k + γ k + 1 e k + 1 + . . . + γ n e n

Поскольку коэффициент вектора e k равен — 1 ≠ 0 , у нас получается нетривиальное представление нуля системой векторов e 1 , e 2 , . . . , e n , а это, в свою очередь, означает, что данная система векторов линейно зависима. Что и требовалось доказать (ч.т.д.).

• Система векторов является линейно независимой, когда ни один из ее векторов нельзя выразить через все остальные векторы системы.
• Система векторов, которая содержит нулевой вектор или два равных вектора, линейно зависима.

Видео:18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать

Свойства линейно зависимых векторов

1. Для 2-х и 3-х мерных векторов выполняется условие: два линейно зависимых вектора — коллинеарны. Два коллинеарных вектора — линейно зависимы.
2. Для 3-х мерных векторов выполняется условие: три линейно зависимые вектора — компланарны. (3 компланарных вектора — линейно зависимы).
3. Для n-мерных векторов выполняется условие: n + 1 вектор всегда линейно зависимы.

Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Примеры решения задач на линейную зависимость или линейную независимость векторов

Проверим векторы a = 3 , 4 , 5 , b = — 3 , 0 , 5 , c = 4 , 4 , 4 , d = 3 , 4 , 0 на линейную независимость.

Решение. Векторы являются линейно зависимыми, поскольку размерность векторов меньше количества векторов.

Проверим векторы a = 1 , 1 , 1 , b = 1 , 2 , 0 , c = 0 , — 1 , 1 на линейную независимость.

Решение. Находим значения коэффициентов, при которых линейная комбинация будет равняться нулевому вектору:

x 1 a + x 2 b + x 3 c 1 = 0

Записываем векторное уравнение в виде линейного:

x 1 + x 2 = 0 x 1 + 2 x 2 — x 3 = 0 x 1 + x 3 = 0

Решаем эту систему при помощи метода Гаусса:

1 1 0 | 0 1 2 — 1 | 0 1 0 1 | 0

Из 2-ой строки вычитаем 1-ю, из 3-ей — 1-ю:

1 1 0 | 0 1 — 1 2 — 1 — 1 — 0 | 0 — 0 1 — 1 0 — 1 1 — 0 | 0 — 0

1 1 0 | 0 0 1 — 1 | 0 0 — 1 1 | 0

Из 1-й строки вычитаем 2-ю, к 3-ей прибавляем 2-ю:

1 — 0 1 — 1 0 — ( — 1 ) | 0 — 0 0 1 — 1 | 0 0 + 0 — 1 + 1 1 + ( — 1 ) | 0 + 0

0 1 0 | 1 0 1 — 1 | 0 0 0 0 | 0

Из решения следует, что у системы множество решений. Это значит, что существует ненулевая комбинация значения таких чисел x 1 , x 2 , x 3 , при которых линейная комбинация a , b , c равняется нулевому вектору. Следовательно, векторы a , b , c являются линейно зависимыми. ​​​​​​​

Видео:Высшая математика. Линейные пространства. Векторы. БазисСкачать

Линейно зависимые и линейно независимые вектора.

Определение. Линейной комбинацией векторов a ₁, . a_n с коэффициентами x ₁, . x_n называется вектор

Видео:Разложение вектора по базису. 9 класс.Скачать

Свойства линейно зависимых векторов:

Видео:4.1. Вектор. Линейные операции над векторамиСкачать

Примеры задач на линейную зависимость и линейную независимость векторов:

Вектора будут линейно зависимыми, так как размерность векторов меньше количества векторов.

Решение: Найдем значения коэффициентов при котором линейная комбинация этих векторов будет равна нулевому вектору.

Это векторное уравнение можно записать в виде системы линейных уравнений

	x 1 + x 2 = 0
	x 1 + 2 x 2 — x 3 = 0
	x 1 + x 3 = 0

Решим эту систему используя метод Гаусса

1 1 0 0 1 2 -1 0 1 0 1 0

из второй строки вычтем первую; из третей строки вычтем первую:

1 1 0 0 1 — 1 2 — 1 -1 — 0 0 — 0 1 — 1 0 — 1 1 — 0 0 — 0

1 1 0 0 0 1 -1 0 0 -1 1 0

из первой строки вычтем вторую; к третей строке добавим вторую:

1 — 0 1 — 1 0 — (-1) 0 — 0 0 1 -1 0 0 + 0 -1 + 1 1 + (-1) 0 + 0

1 0 1 0 0 1 -1 0 0 0 0 0

Данное решение показывает, что система имеет множество решений, то есть существует не нулевая комбинация значений чисел x ₁, x ₂, x ₃ таких, что линейная комбинация векторов a , b , c равна нулевому вектору, например:

а это значит вектора a , b , c линейно зависимы.

Ответ: вектора a , b , c линейно зависимы.

Решение: Найдем значения коэффициентов при котором линейная комбинация этих векторов будет равна нулевому вектору.

Это векторное уравнение можно записать в виде системы линейных уравнений

	x 1 + x 2 = 0
	x 1 + 2 x 2 — x 3 = 0
	x 1 + 2 x 3 = 0

Решим эту систему используя метод Гаусса

1 1 0 0 1 2 -1 0 1 0 2 0

из второй строки вычтем первую; из третей строки вычтем первую:

1 1 0 0 1 — 1 2 — 1 -1 — 0 0 — 0 1 — 1 0 — 1 2 — 0 0 — 0

1 1 0 0 0 1 -1 0 0 -1 2 0

из первой строки вычтем вторую; к третей строке добавим вторую:

1 — 0 1 — 1 0 — (-1) 0 — 0 0 1 -1 0 0 + 0 -1 + 1 2 + (-1) 0 + 0

1 0 1 0 0 1 -1 0 0 0 1 0

из первой строки вычтем третью; к второй строке добавим третью:

1 — 0 0 — 0 1 — 1 0 — 0 0 + 0 1 + 0 -1 + 1 0 + 0 0 0 1 0

1 0 1 0 0 1 0 0 0 0 1 0

Данное решение показывает, что система имеет единственное решение x ₁ = 0, x ₂ = 0, x ₃ = 0, а это значит вектора a , b , c линейно независимые.

Ответ: вектора a , b , c линейно независимые.

Видео:Геометрия 9 класс (Урок№7 - Разложение вектора по двум неколлинеарным векторам. Координаты вектора.)Скачать

Линейная зависимость векторов. Базис на плоскости и в пространстве.

Векторная алгебра. Нелинейные операции над векторами.

3.1.Понятие вектора и линейные операции над векторами.

3.2.Линейная зависимость векторов. Базис на плоскости и в пространстве.

3.3.Нелинейные операции над векторами.

Понятие вектора и линейные операции над векторами.

Опр.1 Вектором называется направленный отрезок, имеющий определенную длину.

Опр.2 Длиной вектора называется его модуль и обозначается символом . Модуль вектора обозначается .

Опр.3 Вектор называется единичным, если его длина равна единице, т.е. .Вектор называется нуль — вектором, если его длина равна нулю, т.е. , обозначается (нуль – вектор не имеет направления, его начало и конец совпадают).

Опр.4 Два вектора называются коллинеарными, если они лежат на одной прямой или параллельных прямых, в противном случае вектора – неколлинеарные. Три вектора называются компланарными, если они лежат в одной плоскости или параллельны одной плоскости, в противном случае вектора – некомпланарными.

Опр.5 Два вектора называются равными, если они коллинеарные, одинаково направленные и имеют одинаковую длину, записывают .

Опр.6 Вектор, образованный из данного вектора параллельным переносом, называется свободным.

Линейные операции над векторами. Линейными операциями называются операции сложения векторов, вычитания векторов и умножение вектора на число.

Опр.7 Суммой нескольких векторов называетсявектор, по величине и направлению равный замыкающей ломаной линии, построенной на свободных векторах, соответствующих данным векторам, его начало совпадает с налом первого, а конец с концом последнего.

Свойства суммы векторов.

Сумма конечного числа векторов обладает переместительным и сочетательным законом.

Опр.8 Сумму двух векторов можно найти по правилу треугольника или правилу параллелограмма.

Опр.9 Под разностью двух векторов и понимают вектор такой, что (разность двух векторов можно найти по правилу треугольника или правилу параллелограмма).

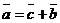
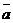
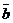
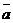
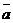
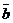
Опр.10 Произведением вектора на скаляр называют вектор = , длина которого равна и направление: совпадает с направлением вектора , если ; противоположно направлению вектора , если . Вектор = , если .

Линейная зависимость векторов. Базис на плоскости и в пространстве.

Опр.11 Векторы называются линейно зависимыми, если существуют числа не все равные нулю, для которых имеет место равенство и если , то векторы называются линейно независимыми.

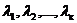
Опр.12Если вектора линейно зависимы и, предположим , то его можно представить в виде линейной комбинации остальных векторов и эти векторы называют базисом, а числа — координатами вектора и обозначают .

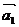
Свойства линейной зависимости векторов.

Свойство 1. Если вектора линейно зависимы, то хотя бы один можно представить в виде линейной комбинации других.

Свойство 2. Если один из векторов представлен в виде линейной комбинации других векторов, то все эти вектора линейно зависимы.

Теорема 1. Всякие три вектора на плоскости линейно зависимы.

Следствие 1. Если на плоскости дано более трех векторов, то они линейно зависимы.

Теорема 2. Для того чтобы два вектора были на плоскости линейно независимыми необходимо и достаточно, чтобы они были неколлинеарными.

Следствие 2. Максимальное число линейно независимых векторов на плоскости два.

Теорема 3. Всякие четыре вектора в пространстве линейно зависимы.

Следствие 1. Если в пространстве дано более четырех векторов, то они линейно зависимы.

Теорема 4. Для того чтобы три вектора были в пространстве линейно независимыми необходимо и достаточно, чтобы они были некомпланарными.

Следствие 4. Максимальное число линейно независимых векторов в пространстве три.

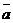
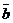
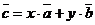
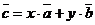
Опр.13 Базисом на плоскости называются два любых линейно независимых вектора. Если и — базисные векторы плоскости, — любой вектор плоскости, тогда — выражается через базисные векторы, а если какой – либо вектор представлен в виде , то говорят, что он разложен по базису и в данном базисе имеет координаты .

Теорема 5. Разложение вектора по базису и является единственным.

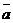
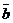
Опр.14 В декартовой прямоугольной системе координат базисные векторы на плоскости обозначаются 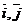и данные векторы единичные, взаимно перпендикулярные.

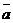
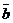
Опр.15 Базисом в пространстве называются три любых линейно независимых вектора. Если , , — базисные векторы пространства, — любой вектор пространства, тогда — выражается через базисные векторы, а если какой – либо вектор представлен в виде , то говорят, что он разложен по базису и в данном базисе имеет координаты .

Теорема 6. Разложение вектора по базису , , является единственным.

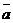
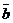
Опр.16 В декартовой прямоугольной системе координат базисные векторы в пространстве обозначаются и данные векторы единичные, взаимно перпендикулярные.

Длина вектора, линейные операции с векторами, заданными в координатной форме.Пусть вектора и разложены по базису и представлены в виде и тогда:

длина вектора находится по формуле ;

сумма векторов находится по формуле = ;

разность векторов находится по формуле = ;

умножение вектора на число находится по формуле .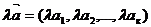

Теорема 7. Если несколько векторов образуют базис, то определитель построенный на их координатах отличен от нуля.

📸 Видео

Урок 1. Матрицы, определитель матрицы и ранг матрицы | Высшая математика | TutorOnlineСкачать

Зачем нужен ВЕКТОР. Объяснение смыслаСкачать

§2 Линейная операция над векторамиСкачать

Линейная зависимость векторов. РангСкачать

Линейные комбинации, span и базисные вектора | Сущность Линейной Алгебры, глава 2Скачать

Линейная комбинация векторовСкачать

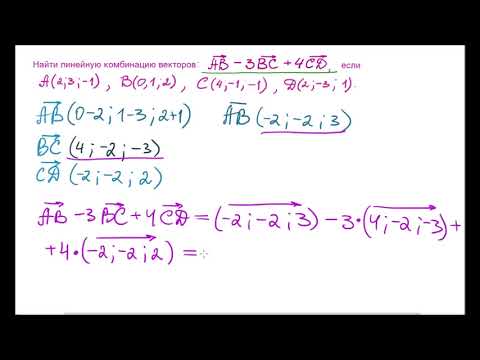
Линейная зависимость векторов. Линейная алгебра. Лекция 2Скачать

Урок 3. Произведение векторов и загадочный угол между векторами. Высшая математика | TutorOnlineСкачать