Лапласиан вектора в цилиндрической системе координат (3 видео)

Оператор Гамильтона. Оператор Лапласа. Понятие о криволинейных координатах

Содержание:

По этой ссылке вы найдёте полный курс лекций по математике:

рассмотрели три основные операции векторного анализа: вычисление gradtx для скалярного поля а и rot а для векторного поля а = а(ж, у, г). Эти операции могут быть записаны в более простом виде с помощью символического оператора V («набла»): Оператор V (оператор Гамильтона) обладает как дифференциальными, так и вектор- ными свойствами.

Формальное умножение, например, умножение ^ на функцию и(х, у), будем понимать как частное дифференцирование: В рамках векторной алгебры формальные операции над оператором V будем проводить так, как если бы он был вектором. Используя этот формализм, получим следующие основные формулы: 1.

Если — скалярная дифференцируемая функция, то по правилу умножения вектора на скаляр получим где P, Q, R — дифференцируемые функции, то по формуле для нахождения скалярного произведения получим Оператор Гамильтона Дифференциальные операции второго порядка Оператор Лапласа Понятие о криволинейных координатах Сферические координаты 3.

Вычисляя векторное произведение [V, а], получим Для постоянной функции и = с получим а для постоянного вектора с будем иметь Из распределительного свойства для скалярного и векторного произведений получаем Замечание 1. Формулы (5) и (6) можно трактовать тамке как проявление дифференциальных свойств оператора «набла» (V — линейный дифференциальный оператор). Условились считал., что оператор V действует на все величины, написанные за ним.

В этом смысле, например, — скалярный дифференциальный оператор.

Применяя оператор V к произведению каких-либо величин, надо иметь в виду обычное правило дифференцирования произведения. Пример 1. Доказать, что По формуле (2) с учетом замечания 1 получаем или Чтобы отметить тот факт, что «набл а» не действует на какую-либо величину, входящую в состав сложной формулы, эту величину отмечают индексом с («const»), который в окончательном результате опускается. Пример 2.

Пусть u(xty,z) — скалярная дифференцируемая функция, а(х,у,г) — векторная дифференцируемая функция. Доказать, что 4 Перепишем левую часть (8) в символическом виде Учитывая дифференциальный характер оператора V, получаем . Так как ие — постоянный скаляр, то его можно вынести за знак скалярного произведения, так что а (на последнем шаге мы опустили индекс е). В выражении (V, иас) оператор V действует только на скалярную функцию и, поэтому В итоге получаем Замечай ие 2.

Используя формализм действа с оператором V как с вектором, надо помнить, что V не является обычным вектором — он не им«ет ни длины, ни направления, так что. например, вектор [V,aJ не будет, вообще говоря, перпендикулярным вектору а (впрочем, для плоского поля вектор перпендикулярен плоскости ,а значит, и вектору а).

Возможно вам будут полезны данные страницы:

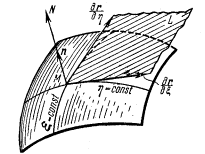
Не имеет смысла и понятие коллинеарности по отношению к символическому вектору V. Например, выражение , где V и ^ — скалярные функции, формально напоминает векторное произведение двух коллинеарных векторов, которое всегда равно нулю. Однако вобшем случае это не имеет места. В самом деле, вектор = grad направлен по нормали к поверхности уровня , а вектор Vy = grad t> определяет нормаль к поверхности уровня i> = const.

Вобшем случае эти нормали не обязаны

быть коллннеарнымн (рис. 40). С другой стороны, в любом дифференцируемом скалярном поле ) имеем Эта примеры показывают, что с оператором «набла» нужно обращаться с большой осторожностью и при отсутствии уверенности в полученном результате его следует проверить аналитическими методами. §12. Дифференциальные операции второго порядка. Оператор Лапласа Дифференциальные операции второго порядка получаются в результате двукратного применения оператора V. 1.

Содержание

Скалярное поле
Цилиндрические координаты
Использование оператора набла для записи операции взятия дивергенции.
Выражение div E в цилиндрической и сферической системах координат.
Уравнение Пуассона и уравнение Лапласа.
Содержание
2. Связь между дифференциалами в декартовой и криволинейной системах координат
Список литературы
Гауссовой кривизной поверхности в данной точке называется величина
Дивергенция вектора имеет вид
🎥 Видео

Скалярное поле

В этом поле оператор V порождает векторное поле В векторном поле grad и можно определить две операции: что приводит к скалярному полю, и что приводит к векторному полю. 2. Пусть задано векторное поле . Тогда оператор V порождает в нем скалярное поле В скалярном поле div а оператор V порождает векторное поле 3.

В векторном поле оператор V порождает также векторное поле Применяя к этому полю снова оператор V, получим: а) скалярное поле Выберем в пространстве прямоугольнуюдекартову систему координат Oxyz и рассмотрим каждую из формул (1)-(5) более подробно. 1. Предполагая, что функция имеет непрерывные вторые частные производные , получим Символ называется оператором Лапласа, или лапласианом. Его можно представить как скалярное произведение оператора Гамильтона V на самого себя,т. е. Оператор Д (дельта) играет важную роль в математической физике.

Уравнение называется уравнением Лапласа. С его помощью описывается, например, стационарное распределение тепла. Скалярное поле и, удовлетворяющее условию , называется лапла-совым или гармоническим полем. Например, скалярное поле является гармоническим во воем трехмерном пространстве: из того, что получаем Оператор Гамильтона Дифференциальные операции второго порядка Оператор Лапласа Понятие о криволинейных координатах Сферические координаты 2.

Пусть функция и имеет непрерывные частные производные второго порядка включительно. Тогда В самом деле, действуя формально, получим ибо как векторное произведение двух одинаковых «векторов». Tor же результат можно получить, используя выражения градиента и ротора в декартовых координатах Пусть задано векторное поле координаты которого P, Q, R имеют непрерывные частные производные второго порядка. Тогда получим 4. При тех же условиях, что и в пункте 3, имеем Это соотношение уже было доказано ранее путем непосредственных вычислений.

Здесь мы приведем его формальное доказательство, используя известную формулу из векторной алгебры Имеем как векторное произведение двух одинаковых «векторов». 5. Покажем, наконец, что при тех же условиях, что и ранее, Так как то, полагая в формуле для двойного векторного произведения получим Поэтому окончательно будем иметь где grad diva выражается по формуле (8), а Да для вектора надо понимать так:. В заключение приведем таблицу дифференциальных операций второго порядка. Скалярное поле Векторное поле Заштрихованные прямоугольники означают, что соответствующая операция не имеет смысла (например, градиент от. § 13.

Понятие о криволинейных координатах Во многих задачах бывает удобно определять положение точки пространства не декартовыми координатами ), а тремя другими числами (qh 42,4з), более естественно связанными с рассматриваемой части ой задачей. Если задано правило, согласно которому каждой точке М пространства отвечает определенная тройка чисел и, обратно, каждой такой тройке чисел отвечает единственная точка М, то говорят, что в пространстве задана криволинейная координатная система.

В этом случае величины ф, называют криволинейными координатами точки М. Координатными поверхностями в системе криволинейных координат qtqi, Яз называются поверхности На координатных поверхностях одна из координат сохраняет постоянное значение. Линии пересечения двух координатных поверхностей называются координатными линиями. В качестве примеров криволинейных координат рассмотрим цилиндрические и сферические координаты. 13.1.

Цилиндрические координаты

В цилиндрических координатах положение точки М в пространстве определяется тремя координатами: (р = const — полуплоскости, примыкающие к оси Oz z = const — плоскости, перпендикулярные оси Oz (рис. 41). Координатные линии: 1) линии (р) — лучи, перпендикулярные оси Oz и имеющие начало на этой оси, т.е. линии пересечения координатных поверхностей у? = const, z = const; 2) линии (ip) — окружности с центрами на оси Oz, лежащие в плоскостях, перпендикулярных оси Oz 3) линии (z) — прямые, параллельные оси Связь декартовых координат точки с цилиндрическими координатами ( задается формулами 13.2.

Сферические координаты В сферических координатах положение точки Af в пространстве определяется следующими координатами: Координатные поверхности (рис.42): г = const — сферы с центром в точке О; • в = const — круговые полуконусы с осью полуплоскости, примыкающие к оси Oz. Координатные линии: 1) линии (г) — лучи, выходящие източки О; 2) линии (в) — меридианы на сфере; 3) линии — параллели на сфере. Связь декартовых координат (х, у, z) точки М с ее сферическими координатами задается формулами.

Введем единичные векторы (орты), направленные по касательным к коор-динатнымлиниям вточке М всторонувозрастанияпеременных qx, q2, соответствен но. Определение. Система криволинейных координат называется ортогональной, если в каждой точке М орты попарно ортогональны. В такой системе ортогональны и координатные линии, и координатные поверхности. Примерами ортогональных криволинейных координат служатсистемы цилиндрических и сферических координат.

Мы ограничимся рассмотрением только ортогональных систем координат. Пусть — радиус-вектор точки М — Тогда можно показать, что Оператор Гамильтона Дифференциальные операции второго порядка Оператор Лапласа Понятие о криволинейных координатах Сферические координаты Аналогично для сферических координат имеем Величины являются дифференциалами длин дуг соответс твующих координатных линий.

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.

Видео:Оператор Лапласа в криволинейных координатахСкачать

Использование оператора набла для записи операции взятия дивергенции.

Ранее было показано, что умножение оператора V на скалярную функцию равносильно взятию градиента от этой скалярной функции. Покажем, что скалярное умножение оператора V на векторную функцию, например, на функцию ?, означает взятие дивергенции от этой векторной функции.

Произведение V ? можно записать так:

Правые части (19.22) и (19.23) равны, следовательно, должны быть равны и левые. Поэтому V? = div?, т. е., действительно, умножение оператора V на вектор ? означает взятие дивергенции от этого вектора.

Видео:§55 Цилиндрическая система координатСкачать

Выражение div E в цилиндрической и сферической системах координат.

Без вывода запишем выражение div Ё:

в цилиндрической системе координат

в сферической системе координат:

Видео:Оператор Лапласа в полярных координатахСкачать

Уравнение Пуассона и уравнение Лапласа.

Эти уравнения являются основными дифференциальными уравнениями электростатики. Они вытекают из теоремы Гаусса в дифференциальной форме. Действительно, известно, что ? = -grad(p. В то же время согласно теореме Гаусса (19.21) div? = р_ск6/е,.

’> Почленно умножаем слагаемые первой скобки на слагаемые второй скобки. Учитываем, что скалярное _произведение одноименных_ ортов, равно единице, а разноименных — нулю: i 1 = j j = к к -1 1 cosO 0 = 1, / j = 7 к = j к = 1 • 1 — cos90° = 0.

Подставим в (19.21) Е из (19.6), получим Вынесем знак минус за знак дивергенции:

Вместо grad(p запишем его эквивалент V ср; вместо div напишем V . Тогда

Уравнение (19.26) называют уравнением Пуассона. Частный вид уравнения Пуассона, когда р_С50б = 0, называют уравнение Лапласа. Уравнение Лапласа записывают так:

Оператор V 2 = div grad называют оператором Лапласа, или лапласианом, и иногда обозначают еще символом Д. Поэтому можно встретить и такую форму записи уравнения Пуассона:

Видео:Объем параболоида: тройной интеграл в цилиндрической системе координатСкачать

Содержание

2. Связь между дифференциалами в декартовой и криволинейной системах координат

Список литературы

Введение

Наблюдая длительный период развития математики, можно заметить, что диалектически происходит периодическая смена двух основных взглядов на восприятие и описание закономерностей окружающей действительности. В одни эпохи идет алгебраизация с ее формализацией и логическим структурированием языка, торжествуют аксиоматические подходы, иногда в ущерб наглядности и даже возможным приложениям. В другие эпохи главенствует геометризация с ее стремлением к интуитивной наглядности, визуализации, к «картинкам», иногда в ущерб даже формальной строгости доказательств. Психологи утверждают, что и индивидуумы делятся на «левополушарных» и «правополушарных», одни из них тяготеют к счету, к абстракции, другие — к наглядности, к геометрии, к моделям.

Сейчас, как нам кажется, имеется тенденция к очередной геометризации, модельности и, следовательно, к воспитанию навыков образного мышления. Мы обращали уже внимание в наших методических указаниях [5] на то, что эта задача становится особенно актуальной в связи с возрастающим количеством нелинейных задач,возникающих в современной физике и технике, решения которых приводят к сложным визуализациям результатов численных расчетов и экспериментов. Мыслительные процессы человека, такие как инженерное проектирование, научно-теоретическое изучение явлений и их связей, оперируют образами, визуальными формами.

Обучение методам образного мышления является большой и серьезной задачей. В данном пособии делается очередной шаг в этом направлении. Учебников и монографий по геометрии много, и неисчислимо много всевозможных методических пособий по тем или иным частным вопросам. Чем же предлагаемые вниманию читателя методические указания отличаются от остальных?

Один из соавторов из личных пристрастий время от времени вкрапляет в читаемый им на физическом факультете курс математического анализа элементы дифференциальной геометрии; другой соавтор в свое время, будучи студентом, активно воспринял эти «вкрапления»; третий, которому удалось продвинуть недавно некоторые трудные вопросы нелинейной физики, поставил второму задачу о большом изгибе мембраны, которую они решали, опираясь на аппарат дифференциальной геометрии, а результат этой работы вышел, по сути, за рамки классической теории. Сама работа получила медаль Российской академии наук на конкурсе научных работ студентов вузов за 1998 год.

Таким образом, дифференциальная геометрия является типичным рабочим инструментом в некоторых актуальных областях современной нелинейной физики и механики. Мы надеемся, что это пособие будет помогать в работе физикам и механикам, как инженерам, так и теоретикам.

Эта работа подготовлена аспирантом (К.Г. Охоткиным) и преподавателями (В.А. Степаненко и Ю.В. Захаровым) и является одним из результатов сотрудничества в рамках Межвузовского инженерно-физического отделения.

Мы благодарны всем, помогавшим изданию работы.

1. Определение поверхности

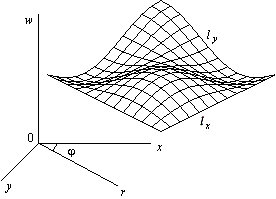
Любой однозначной функции двух переменных w = f ( x , y ) можно поставить во взаимнооднозначное соответствие поверхность (ее график), погруженную в обычное евклидово пространство R 3 , с декартовыми координатами x , y , w . Соответственно в цилиндрических координатах r , φ , w поверхность будет описываться функцией w = f(r, φ) (рис. 1). Такой способ задания поверхности называют явным.

Рис. 1. График поверхности в декартовых координатах

На поверхности можно вводить криволинейную сетку поверхностных координат. Например, l_x , l_y – поверхностные криволинейные координаты, которые получаются в результате сечения поверхности семейством вертикальных плоскостей wox и woy ( рис. 1 ) . Соответственно в цилиндрических координатах можно ввести криволинейные координаты l _r , l _φ , где l _r – криволинейный радиус, получаемый с помощью сечения поверхности плоскостью wor , а l_φ = r φ – дуга окружности. Задаваемые таким образом на поверхности криволинейные координаты являются в общем случае косоугольными (углы между координатными линиями на поверхности не всегда прямые, как в случае ортогональных координат).

2. Связь между дифференциалами в декартовой и криволинейной системах координат

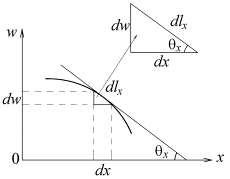
Введем угол наклона касательной θ_x к кривой, получаемой сечением поверхности w = f(x, y) вертикальной плоскостью wo x , в текущей точке x (рис. 2). Аналогично вводятся углы θ _y и θ _r для цилиндрической системы координат.

Рис. 2. Сечение wo x поверхности w = f ( x , y )

Напишем основные выражения, связывающие дифференциалы в декартовой системе координат dx, dy и в криволинейной системе координат dl_x, dl_y. Имеем в сечениях wo x (рис. 2)

, , (1)

, , ; (2)

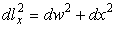
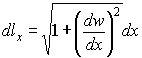
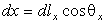
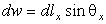
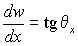
для сечений wo y : , , .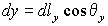

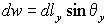
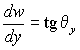
Соответствующие формулы верныив цилиндрических координатах для сечения wo r . Можно также сказать, что формулы (2) задают неявно связь между декартовыми переменными и криволинейными длинами на поверхности, в общем случае x ( l_x , l_y ), y ( l_x , l_y ), z ( l_x , l_y , θ_x , θ_y ).

3. Элемент поверхности. Замена переменных

А. Изменение при переходе из одной системы координат (x, y) в другую (u, v) элемента площади dS₀ в двумерном случае

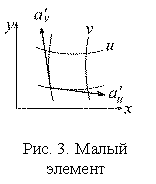
Рассмотрим малый элемент площади dS₀ в плоскости (x, y) (рис. 3).

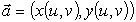
Его дифференциал в произвольном направлении l

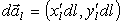
Площадь малого элемента dS₀ построим как модуль векторного произведения двух векторов:

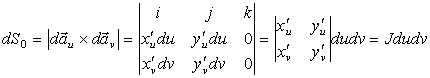
где J – определитель матрицы якобиана перехода. Т.е. dS ₀ = dxdy = Jdudv . В современной дифференциальной геометрии переход осуществляется введением дифференциальной формы ω = dS₀ = dx ^ dy = J du ^ dv, где ^ — внешнее произведение. (См., например, [1], [2] ). Приведем пример для полярной системы координат:

Б. Замена системы координат для элементарной площадки на поверхности

Необходимость выражения дифференциала площади элемента поверхности в различных криволинейных координатах возникает, прежде всего, в процессе вычисления поверхностных интегралов, при переходе к двойному интегралу. Введем обозначения: dS – поверхностный элемент площади (рис. 4), dS ₀ – площадь элемента, лежащего в плоскости xoy , или проекция на эту плоскость dS, т.е. dS₀ = d S cosγ , где , – вектор нормали. Криволинейные ортогональные координаты на поверхности — u , v . Поверхность задана явно, w = f(x, y). Радиус-вектор текущей точки — имеет компоненты:

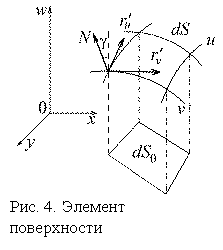
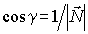
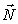
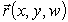
Это задание поверхности в параметрической форме. Построим математическую модель площади с помощью векторного произведения дифференциалов радиус-вектора, аналогично пункту А:

. (3)

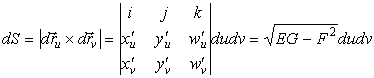
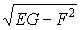
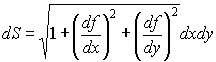
Выражение называется детерминантом первой квадратичной формы, см. следующий пункт, (6). В частном случае, когда в качестве криволинейных координат выбираются собственно декартовые координаты, имеем

Пример : элемент площади в цилиндрических координатах и при осевой симметрии,

когда w = f ( r ) и d / d φ = 0, имеет вид:

. (4)

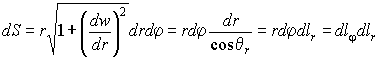
4. Исследование поверхности с помощью аппарата квадратичных форм

А. Первая квадратичная форма I

В каждой точке поверхности можно ввести квадратичную форму

, (5)

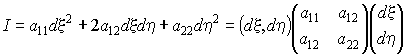
где (ξ, η) – криволинейные поверхностные координаты.

Общеприняты следующие обозначения для коэффициентов формы:

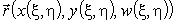
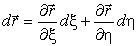
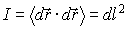
Поясним геометрический смысл первой формы. Пусть – радиус-вектор. Его дифференциал

, (7)

, (8)

где dl – элемент дуги поверхности в произвольном направлении l. Таким образом, первая квадратичная форма определяет квадрат dl. Определим коэффициенты формы, подставив (7) в (8):

, (9)

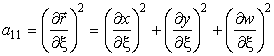
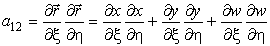
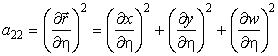
Если χ — угол между касательными векторами (между координатными линиями на поверхности в текущей точке), то 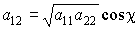. Для ортогональных координат на поверхности χ = π/2, a₁₂ = 0.

Введем обозначение для детерминанта квадратичной формы

. (10 )

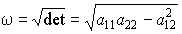
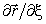
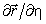
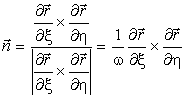
Рассмотрим рис. 5. В текущей точке M построим касательные векторы и . Плоскость L, проведенная через них, является касательной плоскостью к поверхности в точке М. Линия, перпендикулярная к плоскости и проведенная через точку М, является нормалью в текущей точке к поверхности. Ее направление определяется векторным произведением касательных векторов. Единичный вектор нормали находим из следующего выражения:

. (11 )

Рис. 5. Координатные векторы в точке М

Таким образом, первая квадратичная форма описывает поверхность в первом приближении, когда малый участок поверхности заменяется на участок касательной плоскости. Первая квадратичная форма определяет углы между линиями и длины дуг на поверхности, а также площади любых участков поверхности (см. (3) ). Малый элемент площади поверхности

, (12 )

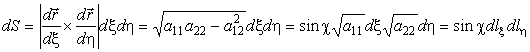
где 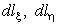— криволинейные дифференциалы на поверхности, получаемые по формулам типа (1), (2) .

Б. Вторая квадратичная форма II

Вторая квадратичная форма описывает поверхность во втором приближении. Она показывает, как отклоняется поверхность от касательной плоскости, и полностью определяет кривизну поверхности.

. (13 )

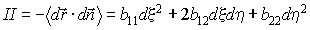
Коэффициенты формы определяются следующими выражениями:

, (14 )

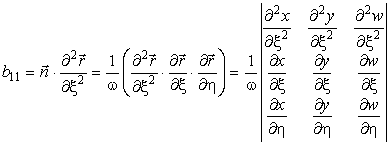
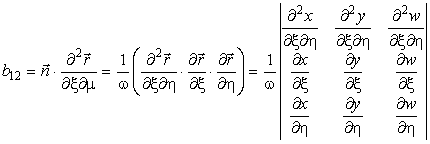
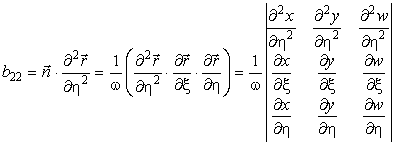
В. Исследование кривизны поверхности

Для двумерного случая скалярной кривизной кривой, лежащей в плоскости, называется величина

, (15 )

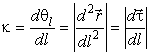
взятая в текущей точке кривой.

Здесь все векторы лежат в одной плоскости. В литературе часто встречаются определения кривизны (15) с разными знаками, которые можно трактовать различно, в зависимости от конкретной задачи. Общий физический смысл: кривизна кривой линии пропорциональна моменту сил, изгибающих ее.

Для пространственного случая нормальной кривизной линии l , получаемой нормальным сечением поверхности, называется величина

, (16 )

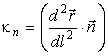
взятая в текущей точке линии. Если вертикальное и нормальное сечения совпадают, то совпадают и величины кривизн (15) и (16). Кривизна κ в произвольном наклонном сечении определяется из (16) по теореме Менье: 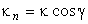, где γ – угол между этим наклонным и нормальным сечениями.

Выберем в качестве параметра, определяющего положение точки на кривой, длину дуги. Тогда криволинейные координаты точки будут функциями длины дуги l: ξ(l), η(l). Выражение (7) перейдет в

. (17 )

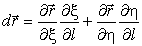
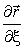
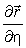
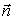
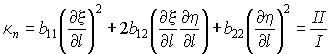
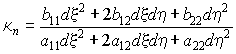
Векторы и перпендикулярны нормали , (см. рис. 5 ). Имеем из (16)

. (18 )

Найдем из (18) нормальные кривизны координатных линий:

1) η = Const, dη = 0, ;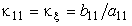

2) ξ = Const, dξ = 0, 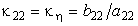. (19 )

Параметр b₁₂/ w определяет кручение поверхности. Проследим за изменением κ_n при повороте сечения вокруг нормали к поверхности. Для гладких поверхностей кривизна будет плавно периодически изменяться от минимального до максимального значения. Найдем их. Перепишем выражение (18) в виде

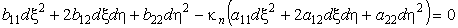
Раскрывая скобки и перегруппировывая члены выражения, имеем

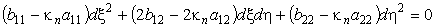
Получили квадратичную форму

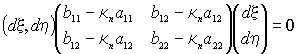
Необходимым и достаточным условием существования нетривиального решения по теореме Крамера является равенство нулю определителя этой матрицы. Имеем квадратное уравнение для кривизны

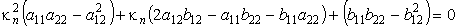
Отсюда находим два экстремальных значения κ_n, которые называются главными кривизнами поверхности в данной точке. Соответствующие им направления (для отношения dξ:dη) называются главными. Главные направления взаимно перпендикулярны.

Проведем линии на поверхности таким образом, чтобы в каждой точке касательные к ним шли вдоль главных направлений. Такие кривые называются линиями кривизны; их удобно выбирать в качестве координатных кривых. Если поверхностная координатная сеть (ξ, η) совпадает с линиями кривизны поверхности, то главные кривизны совпадают с (19) . Если коэффициент первой формы a₁₂ = 0, то это сеть ортогональных криволинейных координат (для них c = p /2); если b₁₂ = 0, то сеть называется сопряженной.

По свойству решений квадратного уравнения имеем для произведения и полусуммы главных кривизн выражения

, .

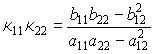
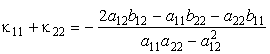
Гауссовой кривизной поверхности в данной точке называется величина

. (20 )

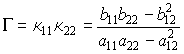
Средней кривизной поверхности в данной точке называется величина

. (21)

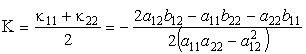
5. Метрический тензор

Пусть дана обычная (лабораторная) система координат x ( x 1 , x 2 , …, x n ). Сделаем переход в произвольную криволинейную (не обязательно ортогональную) систему координат y (y 1 , y 2 , …, y n ). Радиус-вектор и матрица Якоби будет задаваться следующим образом (здесь пишем верхние индексы – используем контравариантные координаты):

, . (22)

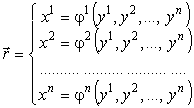
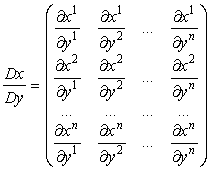
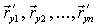
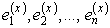
В этой матрице столбцы являются компонентами касательных векторов к координатным линиям y 1 , y 2 , …, y n . Если их нормировать, то получим набор базисных векторов в пространстве x .

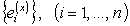
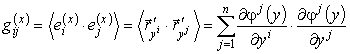
Метрический тензор в базисе имеет вид

. (2 3)

Символы Кристоффеля (коэффициенты связности)

Введем тензорные обозначения касательных векторов и их производных:

, .

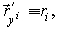
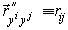
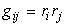
Векторы производных разложим по базисным векторам:

, (24 )

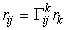
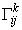
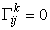
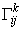
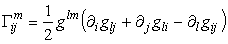
где коэффициенты разложения — некоторые функции координат, вид которых зависит от выбора системы координат; в декартовой системе все . Отсюда видно, что величины не образуют тензора, так как тензор, равный нулю в одной системе координат, равен нулю и во всякой другой. В данной метрике символы Кристоффеля вычисляются по формулам

, (2 5)

доказательство которых приведем ниже.

Найдем, как преобразуется производная от произвольной вектор-функции ∂A i / ∂y j при переходе от декартовых к криволинейным координатам. Для того чтобы получить дифференциал вектора, необходимо, чтобы оба вектора находились в одной точке пространства. Но в криволинейных координатах разность компонент векторов после параллельного переноса их в одну точку не совпадает с их разностью до переноса (т.е. с дифференциалом dA i ). Изменение компонент вектора при бесконечно малом параллельном переносе зависит линейно от самих компонент. Таким образом, запишем точные производные в криволинейных координатах, так называемые ковариантные производные (которые являются тензорами)

, , , (26 )

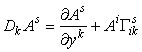
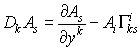
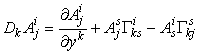
соответственно от контравариантного и ковариантного векторов и тензора. В декартовой метрике они, очевидно, совпадают с обычными производными.

Линия пространства y i = y i ( t ) называется геодезической, если ее вектор скорости A i = dy i / dt параллелен вдоль нее самой, т.е. его ковариантная производная равна нулю.

Уравнение геодезических линий

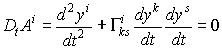
Если все символы Кристоффеля равны нулю, то решениями этого уравнения являются обычные прямые. Таким образом, геодезические линии являются аналогом прямых для случая произвольной кривизны пространства.

Тензор кривизны Римана

Если дважды ковариантно продифференцировать вектор A i , то результат зависит, вообще говоря, от порядка дифференцирования, в противоположность от обычных производных. Запишем эту разность

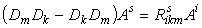
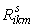
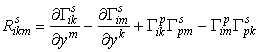
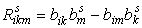
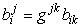
где — тензор 4-го ранга:

, (27 )

, где . (2 8)

Этот тензор называется тензором кривизны Римана данной метрики. Свойства тензора для симметричных связностей:

, .

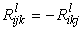
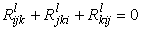
Из тензора Римана можно путем упрощения построить тензор второго ранга — тензор Риччи, являющийся следом тензора Римана

. ( 29)

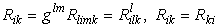
Свернув метрикой тензор Риччи, получим инвариант — след тензора Риччи

, (3 0)

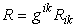
называемый скалярной кривизной данного пространства. Гауссова кривизна, определенная в (19), связана со скалярной следующим образом: 2 K = R .

Тензором кручения пространства называется выражение

. (3 1)

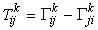
Если связность 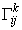является симметричной, то тензор кручения равен нулю. Поясним геометрический смысл тензора кручения на рис. 6. Рассмотрим поверхность S . В точке А к S построим касательную плоскость p . Выберем произвольный бесконечно малый квадрат ABCD на плоскости p с вершиной в А. Из точки А по поверхности S выпустим геодезическую в направлении вектора AB . Пройдя по ней расстояние, соответствующее параметру, равному длине AB , попадем в точку B ‘ . Аналогично из А по S выпустим геодезическую в направлении AD , попадем в D ‘ . Совершим параллельный перенос вектора AD в точку B ‘ вдоль геодезической AB ‘ и выпустим геодезическую из B ‘ вдоль перенесенного вектора, попадем в точку С’. Аналогично вектор AB перенесем параллельно вдоль AD ‘ и вдоль перенесенного вектора из D ‘ выпустим геодезическую, попадем в C » . Если кручение нулевое, то C ‘ = C », и геодезический квадрат с точностью до малых более высокого порядка замкнется, в противном случае нет.

Скалярным произведением двух произвольных векторов

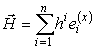
в метрике g_ij будет следующая билинейная форма:

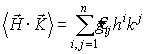
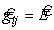
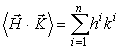
Для частного случая евклидова пространства метрический тензор — единичная матрица, и скалярное произведение принимает обычный вид

Если взять скалярное произведение двух одинаковых векторов, то получим положительно определенную квадратичную форму

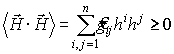
следовательно, det g > 0.

Видео:Оператор набла (оператор Гамильтона) и оператор ЛапласаСкачать

Дивергенция вектора имеет вид

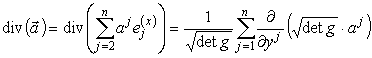
Градиент функции f имеет вид

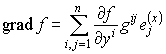
Оператор Лапласа в произвольных криволинейных координатах:

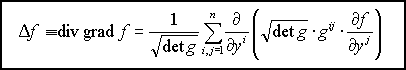Лапласиан вектора в цилиндрической системе координат

В ортогональных криволинейных координатах матрица метрического тензора имеет диагональный вид

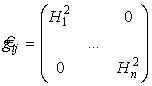
где положительные функции H_i — коэффициенты Ламе системы координат и 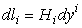. Они соответствуют корням из коэффициентов первой квадратичной формы a ₁₁ и a ₂₂ в теории поверхностей.

Оператор Лапласа в евклидовом пространстве R 3 , в декартовых координатах.

Здесь n = 3, x 1 = x , x 2 = y , x 3 = z . Лапласиан принимает вид

. (33 )

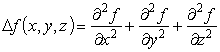
Оператор Лапласа в евклидовом пространстве R 3 , в сферических координатах:

x 1 = r sin θ cos φ , x 2 = r sin θ cos φ , x 3 = r cos θ , (здесь n = 3, y 1 = r , y 2 = θ , y 3 = φ ).

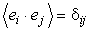
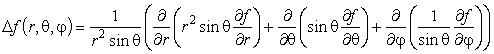
Ортонормированный базис e_r, e _q , e _j , . Лапласиан принимает вид

Оператор Лапласа в евклидовом пространстве R 3 , в цилиндрических координатах:

x 1 = r cos φ, x 2 = r sinφ, x 3 = z. ( здесь n = 3, y 1 = r, y 2 = φ, y 3 = z). Лапласиан принимает вид

. ( 34)

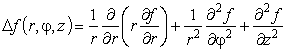
6. Метрический тензор в теории поверхностей

А. Метрика поверхности

Рассмотрим поверхность w = w ( x , y ) в евклидовом пространстве R 3 . Применим для исследования этой поверхности приведенный выше тензорный аппарат дифференциальной геометрии. Будем задавать поверхность в параметрическом виде как геометрическое место точек, описываемых радиус-вектором, проведенным из начала координат (так же, как и при рассмотрении первой квадратичной формы поверхности):

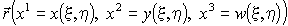
поверхностные криволинейные координаты

Введем тензорные обозначения для производных радиус-вектора поверхности по криволинейным координатам:

; .

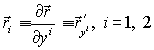
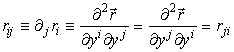
Получим метрический тензор поверхности так же, как и в (23) :

, ( 35)

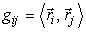
его компоненты образуют матрицу, совпадающую с матрицей первой квадратичной формы поверхности

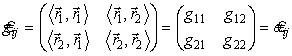
т.е. g_ij = a_ij , и в тензорных обозначениях первая квадратичная форма примет следующий вид:

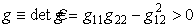
Ковариантные компоненты метрического тензора находим, обращая матрицу

. (3 6)

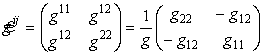
С помощью метрического тензора выполняют операции поднятия и опускания индексов, например, для нахождения ковариантных компонент векторов:

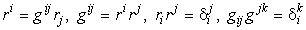
Б. Единичный орт нормали в текущей точке поверхности (см. (11)

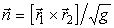
В. Элементарный элемент площади на поверхности

Угол между касательными векторами , .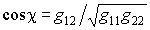

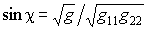
Элемент площади (см. (12)

. (37 )

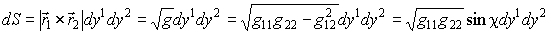
Г. Вторая квадратичная форма записывается в тензорных обозначениях как

II = b_ij dy i dy j , ее коэффициенты вычисляются по формулам

. (3 8)

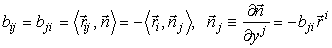
Они подчинены двум уравнениям Петерсона-Кодацци

, i, j, k = 1, 2.

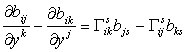
Д. Криволинейный оператор Лапласа записывается так же, как и в (32):

( 39)

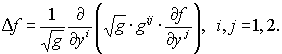
Е. Локальный базис и символы Кристоффеля поверхности

В текущей точке y 1 , y 2 поверхности касательные векторы r ₁ , r ₂ и орт нормали n образуют сопутствующий локальный базис (триэдр) в R 3 , причем

. (40)

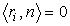
Разложим вектор второй производной в локальном базисе

, (4 1)

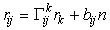
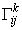
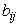
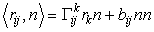
и найдем неизвестные коэффициенты разложения и . Для этого умножим скалярно обе части уравнения (41) сначала на вектор нормали n :

Так как касательные векторы и орт нормали перпендикулярны, то имеем

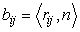
Этот коэффициент действительно совпадает с коэффициентами второй квадратичной формы (38) . Умножим теперь обе части уравнения на касательный вектор :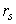

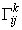
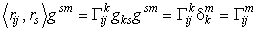
Выразим коэффициенты явно, для этого умножим обе части уравнения на ковариантный метрический тензор

. (4 2)

Скалярное произведение, стоящее в левой части уравнения, можно выразить через компоненты метрики. Продифференцируем метрику 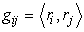по координате и проведем циклические перестановки индексов:

Сложим последние два уравнения и вычтем первое:

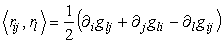
окончательно имеем известное выражение

(43)

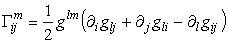
для коэффициентов, которые называются символами Кристоффеля 2 рода. Таким образом, мы получили два уравнения (42) и (43) для нахождения коэффициентов Кристоффеля и уравнение (41) для проверки. Тензор кривизны Римана поверхности определяется так же, как и в (27) .

Рассмотрим заданную явно поверхность w = w ( x , y ) в декартовых координатах:

Имеем радиус-вектор точки поверхности

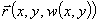
Первые и вторые производные радиус-вектора

, , , , .

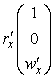
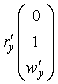
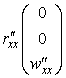
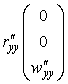
Метрика (матрица первой квадратичной формы) по определению (35)

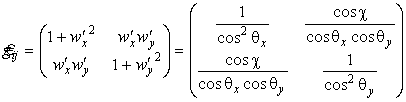
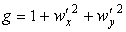
Единичный вектор нормали имеет вид

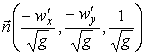
Малый элемент площади поверхности, с использованием соотношений (2)

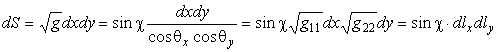
Криволинейный оператор Лапласа в общем косоугольном случае

, (44 )

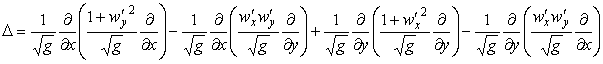
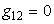
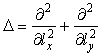
в частном случае поверхности, на которой возникли ортогональные криволинейные координаты (), имеем

Матрица второй квадратичной формы

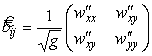
Главные кривизны найдем по формулам (19) :

, . (4 5)

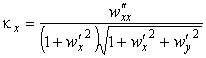
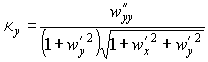
Для осесимметричной поверхности логично перейти в полярные координаты. Если здесь сделать формальную замену переменных (49) , то получим формулы для кривизн в полярных координатах (50) .

В выражениях (45) корень, стоящий в знаменателе, является модулем вектора нормали к поверхности в текущей точке. Если для этой поверхности нормальное сечение совпадает с вертикальным, то кривизны (45) перейдут в

, . (4 6)

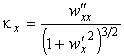
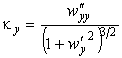
В частном случае малых прогибов поверхности (углов наклона касательной) в выражениях (46) можно пренебречь квадратом производной по сравнению с единицей и получить выражения для малых кривизн (геометрически линейный случай):

, . ( 47)

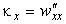
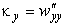
Символы Кристоффеля можно найти по формуле (43) или по формуле (42) :

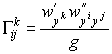
По формулам (27) вычислим компоненты тензора кривизны Римана

, .

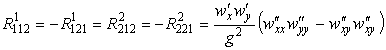
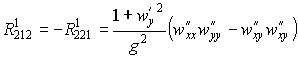
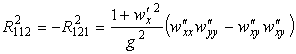
Остальные компоненты равны нулю. Найдем тензор Риччи по формуле (29)

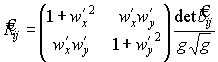
Скалярная кривизна по формуле (30)

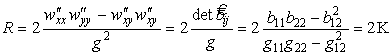
где К — гауссова кривизна, см. формулу (20) .

Рассмотрим осесимметричную поверхность, заданную явно функцией w(r), в цилиндрических координатах. Для этого случая пропадает зависимость от полярного угла φ, и все 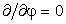, поэтому частные производные по полярному радиусу совпадают с полными производными.

Координаты y 1 = ξ = r, y 2 = η = φ. Используя формулы замены переменных, запишем радиус-вектор

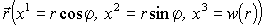
Выпишем производные от радиус-вектора по координатам

, , , , .

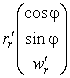
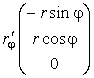
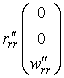
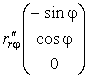
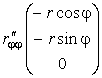
Компоненты метрического тензора (коэффициенты первой квадратичной формы) найдем по формулам (35) или (9):

, , .

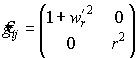
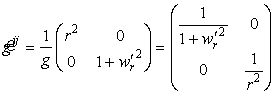
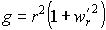
Отсюда видно, что мы получили на поверхности сетку ортогональных криволинейных координат. Оператор Лапласа

. ( 48)

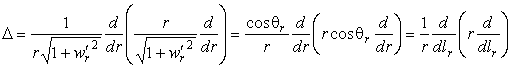
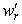
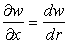
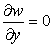
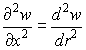
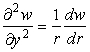
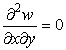
Для случая пологих поверхностей, когда можно пренебречь квадратом производной по сравнению с единицей, оператор (48) совпадает с обычным оператором Лапласа в полярных координатах (см., например, (34) . Выражение (48) можно получить из (44) прямой заменой декартовых координат на полярные для осесимметричного случая. Приведем эти формулы перехода

, , , , . ( 49)

Коэффициенты второй квадратичной формы

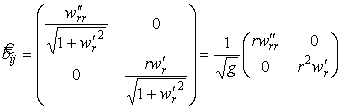
Главные кривизны поверхности найдем по формулам (19) :

, . (5 0)

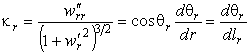
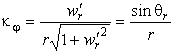
Здесь 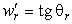, т.е. использована замена переменных w ( r ) на θ ( r ), вида (2) . Выражения (50) можно получить заменой переменных (49) непосредственно из приведенных выше кривизн (45) в декартовой системе координат.

Кручение поверхности отсутствует в осесимметричном случае, так как диагональный коэффициент второй квадратичной формы b ₁₂ = 0. Из (50) видны свойства главных кривизн:

, . ( 51)

, , , .

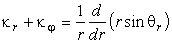
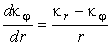
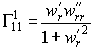
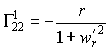
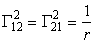
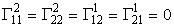
Отличные от нуля компоненты тензора Римана

, .

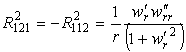
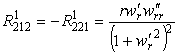
Скалярную кривизну поверхности найдем, дважды свернув тензор Римана

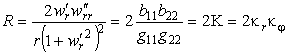
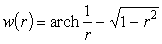
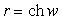
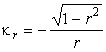
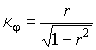
Вычислим для примера главные кривизны псевдосферы — поверхности, образованной вращением трактрисы относительно оси Ow (трактриса является эвольвентой цепной линии ). Используя формулы (50) , найдем кривизны

, .

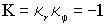
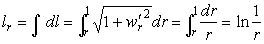
Гауссова кривизна постоянна и отрицательна на всей поверхности. Выполняя интегрирование

получим длину дуги вдоль радиуса на поверхности псевдосферы.

Список литератур ы

1. Дубровин Б.А., Новиков С.П., Фоменко А.Т . Современная геометрия. – М.: Наука, 1985.

2. Новиков С.П., Фоменко А.Т . Элементы дифференциальной геометрии и топологии. – М.: Наука, 1987.

3. Ландау Л.Д., Лифшиц Е.М. Теория поля. — М.: Наука, 1988.

4. Ландау Л.Д., Лифшиц Е.М. Теория упругости. — М.: Наука, 1987.

5. Поверхности функций комплексного переменного: Метод. указания, ч. 5 / Краснояр. гос. ун-т; Сост. Ю.В. Захаров, К.Г. Охоткин, Л.С. Титов. Красноярск, 1996.

6. Победря Б.Е . Лекции по тензорному анализу. — М.: Изд-во МГУ, 1986.