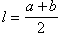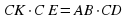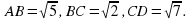Квадрат авсд вписан в окружность хорда се пересекает его диагональ (5 видео)

Задача 16 (С4). Планиметрия. Комбинация окружности и четырехугольника.

Продолжим разговор о различных свойствах окружности, рассмотрим задачи на комбинации окружности и четырехугольника.

Содержание

Конспект занятия «Задача 16 (С4). Планиметрия. Комбинация окружности и четырехугольника.»
Задания по теме для самостоятельного решения
Задание 1
Задание 2
Задание 3
Задача 16 геометрия на ЕГЭ-2021 по математике
Материал по математике «Решение задач по планиметрии»
💥 Видео

Конспект занятия «Задача 16 (С4). Планиметрия. Комбинация окружности и четырехугольника.»

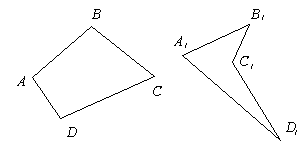
Четырехугольником называется фигура, которая состоит из четырех точек и четырех последовательно соединяющих их отрезков. При этом никакие три из данных точек не лежат на одной прямой, а соединяющие их отрезки не пересекаются.

Две несмежные стороны четырехугольника называются противоположными. Две вершины, не являющиеся соседними, называются также противоположными.

Параллелограммом называется четырехугольник, у которого противолежащие стороны попарно параллельны.

Свойства параллелограмма

противолежащие стороны равны;

противоположные углы равны;

диагонали точкой пересечения делятся пополам;

сумма углов, прилежащих к одной стороне, равна 180°;

сумма квадратов диагоналей равна сумме квадратов всех сторон:

Четырехугольник является параллелограммом, если:

Две его противоположные стороны равны и параллельны.

Противоположные стороны попарно равны.

Противоположные углы попарно равны.

Диагонали точкой пересечения делятся пополам.

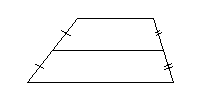
Трапецией называется четырехугольник, у которого две противолежащие стороны параллельны, а две другие непараллельны.

Параллельные стороны трапеции называются ее основаниями, а непараллельные стороны — боковыми сторонами. Отрезок, соединяющий середины боковых сторон, называется средней линией.

Трапеция называется равнобедренной (или равнобокой), если ее боковые стороны равны.

Трапеция, один из углов которой прямой, называется прямоугольной.

ее средняя линия параллельна основаниям и равна их полусумме;

если трапеция равнобокая, то ее диагонали равны и углы при основании равны;

если трапеция равнобокая, то около нее можно описать окружность;

если сумма оснований равна сумме боковых сторон, то в нее можно вписать окружность.

Четырехугольник является трапецией, если его параллельные стороны не равны

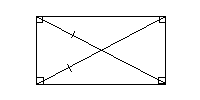
Прямоугольником называется параллелограмм, у которого все углы прямые.

Свойства прямоугольника

все свойства параллелограмма;

Параллелограмм является прямоугольником, если:

Один из его углов прямой.

Его диагонали равны.

Ромбом называется параллелограмм, у которого все стороны равны.

Свойства ромба

Все свойства параллелограмма;

диагонали являются биссектрисами его углов.

Параллелограмм является ромбом, если:

Две его смежные стороны равны.

Его диагонали перпендикулярны.

Одна из диагоналей является биссектрисой его угла.

Квадратом называется прямоугольник, у которого все стороны равны.

Свойства квадрата

все углы квадрата прямые;

диагонали квадрата равны, взаимно перпендикулярны, точкой пересечения делятся пополам и делят углы квадрата пополам.

Прямоугольник является квадратом, если он обладает каким-нибудь признаком ромба.

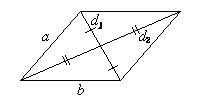
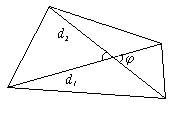
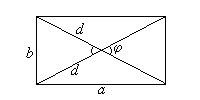
Произвольный выпуклый четырехугольник
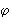
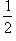
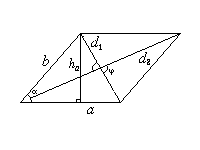
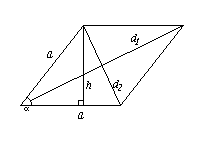
d₁, d₂ — диагонали; — угол между ними; S — площадь.

S =d₁d₂ sin

Параллелограмм
a и b — смежные стороны; 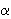— угол между ними; h_a— высота, проведенная к стороне a.

S = ab sin

S =d₁d₂ sin

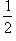
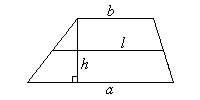
Трапеция
a и b — основания; h — расстояние между ними; l — средняя линия.

Прямоугольник

S =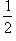d₁d₂ sin

Ромб

S = a 2 sin

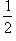
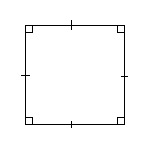
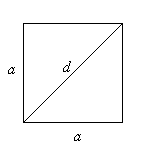
S =d₁d₂

Квадрат
d — диагональ.

S =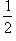d 2

Определить острый угол ромба, в котором сторона есть среднее геометрическое его диагоналей.

На сторонах квадрата ABCD отмечены точки M , N и K , где M – середина AB , N лежит на стороне BC , причем 2 BN = NC , K лежит на стороне DA , причем 2 DK = KA . Найти синус угла между прямыми MC и NK .

В параллелограмме ABCD биссектрисы углов при стороне AD делят сторону BC точками M и N так, что BM : MN = 1 : 2. Найдите BC если AB = 12.

В параллелограмм вписана окружность.

а) Докажите, что этот параллелограмм — ромб.

б) Окружность, касающаяся стороны ромба, делит её на отрезки, равные 3 и 2. Найдите площадь четырёхугольника с вершинами в точках касания окружности со сторонами ромба.

Сторона CD прямоугольника ABCD касается некоторой окружности в точке M. Продолжение стороны AD пересекает окружность в точках P и Q, причём точка P лежит между точками D и Q. Прямая BC касается окружности, а точка Q лежит на прямой BM.

б) Известно, что CM = 17 и CD = 32. Найдите сторону AD.

Квадрат ABCD вписан в окружность. Хорда CE пересекает его диагональ BD в точке K.

а) Докажите, что

б) Найдите отношение CK и KE, если .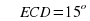

Четырехугольник ABCD вписан в окружность. Прямые AB и CD пересекаются в точке P .

а) Докажите, что AD * BP = BC * DP .

б) Найдите площадь треугольника APC , если известно, что BD =2 AC , а площадь четырехугольника ABCD равна 36.

Высота равнобедренной трапеции ABCD (В C и AD — основания) равна длине ее средней линии.

а) докажите, что диагонали трапеции перпендикулярны.

б) Найдите радиус окружности, касающейся сторон AB , BC и CD трапеции, если известно, что BC =4, AD =6.

Четырехугольник ABCD со взаимно перпендикулярными диагоналями AC и BD вписан в окружность.

а) Докажите, что квадрат диаметра окружности равен сумме квадратов противоположных сторон четырехугольника.

б) Найдите площадь четырехугольника ABCD , если известно что

Видео:ЕГЭ-2016. Математика. Задание 16 (планиметрия)Скачать

Задания по теме для самостоятельного решения

Задание 1

Основания равнобедренной трапеции равны 8 и 6. Радиус описанной окружности равен 5. Найдите высоту трапеции.

Задание 2

Биссектриса угла ADC параллелограмма ABCD пересекает прямую AB в точке E. В треугольник ADE вписана окружность, касающаяся стороны AE в точке K и стороны AD в точке T. Найдите угол BAD, если известно, что AD = 6 и KT = 3. Ответ запишите числом в градусах без пробелов и знаков препинания.

Задание 3

В четырёхугольнике ABCD известно, что ABD = ACD = 45 o , BAC = 30 o , BC = 1. Найдите AD. В ответ запишите квадрат искомой величины.

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Задача 16 геометрия на ЕГЭ-2021 по математике

На этой странице — обзор разных типов заданий № 16 ЕГЭ-2021 по математике, то есть задач по геометрии.

Все они имеют нечто общее: во-первых, это стандартный уровень сложности, то есть вполне решаемые задачи. Пункт (а) в них вообще простой.

Во-вторых, в каждой из них применяются свойства четырехугольников, вписанных в окружности.

В первой задаче такая окружность находится почти сразу, причем она – вспомогательная, и ее можно даже не изображать на чертеже. Главное – найти равные вписанные углы, опирающиеся на равные дуги или на одну дугу.

Также здесь использована формула синуса тройного угла. Если вы ее забыли – не беда. Ведь а формулу синуса суммы вы знаете.

1. Дана равнобедренная трапеция ABCD, в которой меньшее основание ВС равно боковой стороне. Точка Е такова, что ВЕ перпендикулярно AD и СЕ перпендикулярно BD.
а) Доказать, что угол АЕВ равен углу BDA.
б) Найти площадь трапеции ABCD, если АВ = 32, косинус угла АDВ равен

– равнобедренный, CM – высота, проведенная к основанию, значит, M – середина BD.

Докажем, что точки A, B, C, D, E лежат на одной окружности.

ABCD – равнобедренная трапеция, ее можно вписать в окружность.

В – медиана и высота, значит, равнобедренный, BE = ED.

Тогда по трем сторонам, четырехугольник BCDE можно вписать в окружность, т.к.

Так как вокруг можно описать только одну окружность и вокруг четырехугольников ABCD и BCDE тоже можно описать окружность, точки A, B, C, D, E лежат на одной окружности, так как опираются на одну и ту же дугу AB (точки E и D лежат по одну сторону от прямой AD).

б) Так как AB = BC = CD, то дуги AB, BC и CD также равны.

Четырехугольник ABDE вписан в окружность, тогда

По формуле синуса тройного угла,

тогда по теореме синусов

Проведем в трапеции ABCD высоту CK, тогда

BH и CK – высоты трапеции, а так как трапеция равнобедренная, то

Во второй задаче мы увидим ту же идею: вспомогательную окружность. Это один из методов, помогающих решать задачи ЕГЭ по геометрии. Есть здесь и другой мощный прием – использование двух пар подобных треугольников. И еще свойство высоты прямоугольного треугольника, проведенной к гипотенузе. Если вы в восьмом и девятом классе учили геометрию – вы должны владеть этими приемами.

2. Дан прямоугольный треугольник АВС с прямым углом С. Из вершины С на гипотенузу опущена высота СН, на АС и ВС соответственно отмечены точки М и N так, что угол MHN – прямой.
а) Докажите, что треугольники МNH и АВС подобны.
б) Найдите СN, если АС = 5, СМ = 2, ВС = 3.

а) Рассмотрим четырехугольник CMHN.

по условию, значит, CMHN можно вписать в окружность; вписанные, опираются на дугу HN.

Запишем соотношение сходственных сторон.

По условию, AM = 3, найдем CH — высоту

по теореме Пифагора,

AH — проекция катета AC на гипотенузу, по свойствам прямоугольного треугольника, отсюда

В следующей задаче мы снова видим окружность и вписанную в нее трапецию. И наверное, вы уже заметили: пункт (а) задач по геометрии на ЕГЭ часто оказывается подсказкой для решения пункта (б). То, что мы доказали в (а), мы используем в пункте (б).

3. Даны 5 точек на окружности: A, B, C, D, E, причем АЕ = ED = CD, ВЕ перпендикулярен АС.
Точка Т – точка пересечения АС и BD.
а) Докажите, что отрезок ЕС делит отрезок ТD пополам.
б) Найдите площадь треугольника АВТ, если BD = 10, АЕ =

Докажем, что M — середина TD.

Если AE = ED = DC, то дуги AE, ED, DC, также равны;

— накрест лежащие, при пересечении AC и DE секущей CE, значит, AEDC — равнобедренная трапеция. значит, BD — диаметр окружности.

(опирается на диаметр), по катету и гипотенузе, тогда DM — биссектриса равнобедренного т.к. — равнобедренный, то DM — медиана M — середина CE, кроме того, DM — высота

В — медиана и высота, значит, — равнобедренный, а так как — накрест лежащие, при параллельных прямых AC и DE и секущей CE, то по боковой стороне и углу при основании, тогда

CDET — ромб, M — точка пересечения его диагоналей, M — середина TD.

Мы нашли, что AE = ED = CD = CT = ET.

BD = 10 — диаметр окружности.

— равнобедренный, AE = ET, — высота и медиана

Тогда BN — медиана и высота — равнобедренный, AB = BT.

Обозначим тогда — опираются на дугу AE,

Из по теореме синусов:

И еще одна трапеция, вписанная в окружность. Теперь вы точно выучите ее свойства наизусть! Также здесь применяется теорема о пересекающихся хордах. Все эти полезные теоремы, свойства и признаки можно найти в нашей универсальной шпаргалке – Справочнике Анны Малковой для подготовки к ЕГЭ по математике. Скачать Справочник бесплатно можно здесь.

4. Трапеция с большим основанием AD и высотой ВН вписана в окружность. Прямая BH пересекает окружность в точке К.

б) Найдите AD, если: радиус окружности равен шести, СК пересекается с AD в точке N и площадь четырехугольника BHNC в 24 раза больше, чем плошать треугольника KHN.

а) Трапеция ABCD вписана в окружность, следовательно, AB = CD (трапеция равнобокая)

Тогда — вписанные, опираются одну и ту же на дугу AK;

следовательно, CK — диаметр окружности, так как вписанный угол, опирающийся на диаметр, прямой; — опирается на диаметр CK, значит,

(опираются на дугу BC), тогда

Обозначим так как HE = BC,

Из подобия треугольников KNH и KCB следует, что тогда

По теореме о пересекающихся хордах,

Представив левую часть уравнения как разность квадратов, получим:

По смыслу задачи тогда и значит

Задача по геометрии на ЕГЭ по математике оценивается в 3 балла. Как видите, в 2021 году эти 3 балла за геометрию можно было получить без особенных трудностей. На нашем Онлайн-курсе подготовки к ЕГЭ мы решаем и такие задачи по геометрии, и более сложные. Если ты сейчас в 10-м или в 11-м классе – попробуй бесплатно Демо-доступ к Онлайн-курсу.

5. (Резервный день) Окружность с центром О, построенная на катете АС прямоугольного треугольника АВС, как на диаметре, пересекает гипотенузу АВ в точках А и D. Касательная, проведенная к этой окружности в точке D, пересекает катет ВС в точке М.

А) Докажите, что ВМ = СМ
Б) Прямая DM пересекает прямую АС в точке Р, прямая ОМ пересекает прямую ВР в точке К.

Найдите ВК : КР, если

а) Так как – радиус окружности, – равнобедренный, так как (касательная перпендикулярна радиусу, проведенному в точку касания), тогда

– угол между касательной и хордой,

Тогда т.е. – высота – прямоугольный, – равнобедренный, отсюда

Найдем BK : KP, если тогда

Значит, (вертикальные), — равнобедренный, тогда так как MK – биссектриса

Видео:Математика 11, задача по геометрии, 2-я часть ЕГЭ, задача 16Скачать

Материал по математике «Решение задач по планиметрии»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Развитие управляющих функций мозга ребёнка: полезные советы и упражнения для педагогов

Сертификат и скидка на обучение каждому участнику

ШХема 1. ‘Удлинение медианы

Пример 1. В трапеции АВСД (ВС//АД) М и N — середины ВС и

АД, АС — л/15, ВД = 1, MN = 2. Найти S трапеции.

Построить треугольник по двум сторонам и медиане к третьей.

Построить треугольник по трем медианам.

В равнобедренном треугольнике с боковой стороной равной 4 проведена медиана боковой стороны, равная 3. Найти основание треугольника.

Стороны АВ и АС ААВС равны 8 и 6. В каких пределах изменяется медиана AM?

Внутри угла взята точка М, провести через точку М прямую так, чтобы отрезок, заключенный между сторонами угла, делился точкой М пополам.

В трапеции АВСД основание АД в 3 раза больше основания ВС=а. Биссектриса ZA= 45° проходит через середину боковой стороны СД. Найти площадь трапеции.

В прямоугольном Д ABC ZB=90°, ВН — высота, AM — медиана, они пересекаются в точке Р. Найти длину катета АВ, если ВР=Ю,РН=2.

Высота, проведенная к гипотенузе прямоугольного треугольника, делит ее на части 4 и 9 см. Из вершины большего острого угла треугольника проведена прямая, проходящая через середину высоты. Найти длину отрезка этой прямой, заключенного внутри данного треугольника.

а, Ъ, с — стороны треугольника, т _с — медиана к стороне, раиной с. Установить связь между а, Ь, с, т _с . (Иначе, доказать:

В A ABC на продолжении медианы ВМ выбрана точка К так, 410 МК:ВМ=-.2, АВ=5, ВС=3, СК=4. Найти АК.

ЛТема 2. Метод вспомогательной площади

Задача. В прямоугольном A ABC (ZC= 90°), СД — высота.

Радиусы окружностей, вписанных в А АСД и АДСВ соответственно

равны г 1 и г 2 . Найти радиус окружности, вписанной в A ABC.

По данным катетам а и Ъ определите высоту, проведённую к гипотенузе.

Доказать, что сумма расстояний от любой точки, лежащей внутри равностороннего треугольника, до его сторон не за зисит от выбора этой точки.

Если БД — биссектриса ААВС, то

В треугольник со сторонами а, Ъ и с вписан полукруг с диаметром, лежащим на стороне с. Найги радиус полукруга.

Определить острый угол ромба, в котором сторона есть срзднее пропорциональное между диагоналями.

В /SABC радиус вписанной окружности равен S, расстояние от её центра до вершины С равно 5, сторона АВ= 4 -Js . Найти АС и СВ.

Один из острых углов прямоугольного треугольника равен 30°, а катет, лежащий против этого угла, равен а. Через вершину прямого угла проведена окружность, касающаяся гипотенузы и отсекающая от катетов хорды равной длины. Найти её радиус.

В прямоугольник со сторонами 6 и 8 вписан ромб площади 36 так, что на каждой стороне прямоугольника лежит по одной вершине ромба. Найти длины диагоналей ромба.

Дан ромб ABC Д. На сторонах АВ взяты точки М и N так, что отрезки МС и NC делят ромб на три равновеликие части. Найти отрезок МЛ Г , если диагональ ВД= 6.

В A ABC вписана окружность, которая касается сторон АС и ВС в точках К и Д соответственно. Найти cos ZABK, если КС= 20, ВД= 10, cosZBCA- 3.

В A ABC АС=СВ= 10, АВ= 2. Окружность, построенная на боковой стороне как на диаметре, пересекает остальные стороны в точках Н и Р. Найти Sahpc-

Ш’ема 3. Медиана, проведенная ^гипотенузе

Теорема. Медиана, проведенная к гипотенузе, равна ее половине.

Верно и обратное утверждение.

Следствие. Центр описанной окружности около прямоугольного треугольника лежит на середине гипотенузы.

Медиана, проведенная к гипотенузе прямоугольного треугольника, равна т и делит прямой угол в отношении 1:2. Найти стороны треугольника.

В треугольнике ABC медианы ВВ _> и СС. пересекаются в точке М и взаимно перпендикулярны. Найти МА, если BBj= 36, ССу=15..

Доказать, что высота и медиана, проведенные к гипотенузе образуют угол, равный разности острых углов треугольника.

Гипотенуза прямоугольного треугольника в 4 раза больше проведенной к ней высоты. Найти острый угол треугольника.

Окружности касаются внешним образом в точке С, в которую проведены хорды С А и СВ, где А В — внешняя касательная. Найти угол АС В.

В трапеции АВСД, вписанной в окружность радиуса 2 см, диагональ АС является биссектрисой Z -ВАД, а АД больше основания ВС в 2 раза. Найти площадь трапеции.

В трапеции АВСД основания АВ и СД имеют длины 5 и 3, соответственно, боковая сторона АД перпендикулярна основаниям. На основании СД как на диаметре построена окружность, которая пересекает диагонали АС и ВД в точках F и Е. Известно, что Е — середина ВД. Найти в каком отношении точка F делит отрезок АС.

Через вершину А некоторого угла проведена окружность, пересекающая стороны угла в точках В и Д, а его биссектрису в точке С. Найти величину угла В АД, если 3 _АВСД = Зл/З, и АВ+АД= 6.

Две окружности радиусов 3 и 2 касаются друг друга внешним образом. Трапеция АВСД расположена так, что ее основания АВ и СД являются диаметрами этих окружностей. Площадь

трапеции . Найти ВС и АД.

Шема 4. Свойства пересевающихся хррЬ. касательная и секущая

Ключевая задача №1. Произведение отрезков хорды есть величина постоянная, равная R

d, где d — расстояние от центра до точки пересечения хорд.

Ключевая задача №2. Пусть к окружности проведены касательная и секущая, тогда квадрат касательной равен произведению секущей на её внешнюю часть.

Задан равнобедренный ЬЛВС с основанием АС. Окружность радиуса 2^5 касается прямой АС в точке А, боковой стороны ВС в точке D и пересекает боковую сторону АВ в точкг М. Найти периметр А АБС, если известно, что АМ:МВ

В равнобедренном Л ABC. с основанием АС вписа-шая окружность касается боковой стороны ВС в точке Q, а отрезок AQ пересекает вписанную окружность в точке Р. Ншти площадь A ABC, если АС= 12, PQ=5.

Вершины М.ВС лежат на окружности, АВ:ВС=2:3. Точка D делиг дугу АС пополам, BD пересекает АС в точке Е. Через точку Е проведена хорда КМ, КЕ

На диаметре CD окружности выбрана точка Е. Через эту точку проведена хорда АВ, АЕ=4, ВЕ= 3, AD= 6,5; ZABC=60°. Найти СЕ и ED.

В A ABC ZB — тупой. Постройте на основании АС точку D такую, что BA 2 -AD р(С.

В параллелограмме ABCD сторона ВС в два раза больше стороны АВ. Окружность, проходящая через вершины А, В и С, пересекает продолжение стороны CD в точке К, продолжение стороны AD в точке М. АМ= 15, СК—Х2. Найти площадь параллелограмма.

В A ABC сторона АВ-15. Окружность, проходящая чгрез вершину С, касается стороны АВ в точке L и пересекает стороны АС и ВС в точках Р и Q, соответственно. Найти АС и ВС, если известно, что АР= 3, В0=2 и CL — биссектриса Z.C.

В остроугольном равнобедренном A ABC с основанием АС проведена высота АН, продолжением которой пересехает описанную около треугольника окружность в точке D. Найти площадь ААВС, если АН= 9, AD= 13.

91Тема S. (Вписанный угол. Угол мелфу касательной и гордой

Теорема. Вписанные углы, опирающиеся на одну дугу, равны.

Следствие. Вписанный угол, опирающийся на диаметр, прямой.

Теорема. Угол, образованный касательной и хордой, проведенной в точку касания, равен половину дуги, заключенной между ними.

Дана окружность с центром в точке О. Провести касательную из точки М вне окружности.

Угол при вершине равнобедренного треугольника равен 40°. Одна из боковых сторон служит диаметром полуокружности, которая делится другими сторонами на три дуги. Найти градусные меры этих дуг.

Через точку касания двух окружностей проведены две секущие, концы которых соединены хордами. Доказать, что эти хорды параллельны.

Из точки С окружности на хорду АВ опущен перпендикуляр СД. Из концов хорды опущены перпендикуляры АЕ и BF на касательную к окружности в точке С. АЕ = 9, BF = 4. Найти СД. (Или доказать, что СД 2 = AE BF).

Две окружности, касающиеся друг друга внешним образом в точке Д. Прямая касается одной из них в точке А, а другую пересекает в точках В и С. Докажите, что точка А равноудалена от прямых ДВ и СД.

Пользуясь одной линейкой проведите перпендикуляр из заданной точки А, лежащей вне окружности на заданный диаметр СД.

Шар радиуса 2 касается конуса в точке М, высоту конуса КС (К — вершина) надо найти, если А — точка касания шара плоскости основания конуса, Д — её диаметрально противоположная точка, Д-М-С — прямая, АС = 1.

В прямоугольной трапеции АВСД большее основание АД в 3 раза меньше высоты АВ. Через точки А, В и С проведена окружность. Найти острый угол трапеции, если площадь круга в 71 раз больше площади трапеции.

Дан ромб АВСД. Окружность радиуса R описана около Д АВД и проходит через центр окружности, вписанной в Д СВД. Найти площадь ромба.

В прямоугольном треугольнике ABC, ZB=90°, биссектриса BE прямого угла делится центром О вписанной окружности в отношении ВО : ОЕ = %/з : -Jl . Найти острые углы треугольника.

Найдите площадь прямоугольного треугольника, если радиус вписанной окружности — 3, а описанной — 8.

Пятиугольник АВСДЕ вписан в окружность радиуса 1. Известно, что ZBCE = 75°, ZCEA = 90°, ВС = Л, ДС — АЕ. Найти площадь пятиугольника.

Две окружности радиусов 3 и 4, расстояние между центрами которых равно 5, пересекаются в точках А и В. Через точку В проведена прямая, которая пересекает окружность в точках С и Д. (С-В-Д), СД= 8. Найти Б _мсд .

Около прямоугольного треугольника ABC с катетами АС— 5, ВС= 12 описана окружность. Точки Ми N- середины меньших дуг АС и ВС этой окружности, К — середина дуги АВ, не содержащей точки С. Найти S _AMNK .

‘ ЛГема 6. УТараллельные прямые, пересекающие стороны угла

В равнобедренном треугольнике ABC (АС=СВ) проведена медиана CCi и биссектриса АА,. Найти ZACB, если AAj=2

В равнобедренном треугольнике АБС ( АС=СВ ) отношение ьысоты AD к основанию ВС равно V3- Точка М взята на

стороне АВ так, что i . Найти величину у 1 ‘ла МСВ.

Высота ВК ромба ABCD, опущенная на сторону AD, пересекает диагональ АС в точке М. Найти MD , если ВК=4, AK:KD=1:2.

Постройте отрезок _Х -°Ь, где а, Ь, с — данные отрезки. Почему

х называют четвертым пропорциональным?

Е>ысота CD треугольника ABC делит медиану ВМ в отношении 3:1, считая от вершины В. В каком отношении CD делит сторону АВ, считая от вершины А.

В треугольник вписан прямоугольник так, что две его вершины лежат на боковых сторонах, а две — на основании.

Диагонали прямоугольника параллельны боковым сторонам. В каком отношении вершины прямоугольника делят боковые стороны.

В остроугольном треугольнике ABC длины медиан ВМ, CN и высоты АН равны, соответственно, 4, 5 и 6 см. Найти площадь треугольника ABC.

D — середина стороны АС треугольника ABC. Q — точка пересечения медиан треугольника DBC. AQl DC=M. Найти ВМ.МС.

Вершины правильного треугольника расположены на трёх параллельных прям ых. Расстояние от средней прямой до двух крайних V 2 T и V84 • Найдите стороны треугольника.

В треугольнике ABC на стороне А В выбрана точка D так, что BD:AD=4:1. Точки O _t и 0 ₂ — центры окружностей, описанных около треугольника ACD и BCD. Известно, что прямая 0/0 ₂ \ВС. Определить, в каком отношении прямая OjOj делит площадь треугольника ABC.

0.ТГема 7. формула a-2^ina

Ключевая задача. Хорда окружности равна произведению

диаметра на синус вписгнного угла, опирающегося на эту хорду.

Основания равнобедренной трапеции равны 36 и 12. Определить радиус окружности, описанной около трапеции, если её боковая сторона равна 16.

В окружность радиуса R вписан треугольник с углами 15° и 60°. Найти его площадь.

В равнобедренном треугольнике центр вписанной окружности делит высоту, проведённую к основанию, на отрезки 5 и 3, считая от вершины. Найти радиус описанной окружности.

Радиус окружности, описанной около треугольника, равен R, его углы а, [3. у. Найти площадь треугольника.

В равнобедренной трапеции основания равны 21 и 9, высота 8. Найдите радиус описанного круга.

Из точки М на окружности проведены три хорды: MN- 1, МР= 6, MQ= 2. При этом Z.MNP-Z. PMQ. Найти радиус окружности.

В трапеции ABCD, вписанной в окружность радиуса 2 см, диагональ АС является биссектрисой угла BAD, а длина основания AD в два раза больше длины основания ВС. Найти площадь трапеции.

Точка А внутри круга радиуса R удалена от центра О круга на расстояние, равное а. Через точку А проведены две хорды, образующие углы в 30° с диаметром АО. Найти площадь вписанного в круг четырехугольника, диагонали которого совпадают с проведенными хордами.

В ААВС АВ>ВС, АС= 5л/3 . На АВ выбрана точка М так, что ВМ=ВС. Радиус окружности, описанной около А АМС, равен 2л/5 .Найти радиус окружности, описанной около ААВС.

Через вершины А и В ААВС проведена окружность радиуса 4, пересекающая стороны АС и ВС в точках D и Е, соответственно. Найти радиус окружности, описанной около A CDE, если BD= 5, CD=. 2.

В ААВС проведена высота ВН, основание которой лежит на стороне АС. АВ= 8, ВС= 4, АН=5НС. Найти радиус описанной окружности.

В треугольнике один из углов 60 е , радиус описанной окружности равен _7_, а радиус вписанной окружности 3.

Найти площадь треугольника.

Около равнобедренного ААВС (АВ=ВС) с углом 30° описана окружность S радиуса R, AD — её диамегр, проведённый из А. Найти радиус окружности, касающейся стороны АС данного треугольника, диаметра AD и окружности S.