Через вершину b треугольника abc проведена прямая параллельная прямой ac

Ответ:

1) При проекции точки B и B1 будут совпадать, так как тВ уже принадлежит этой плоскости.

как следствие BA1=B1A1 и ВС1=В1С1

2) Так как АС параллельна плоскости, то ее проекция А1С1=AC.

3) Рассм треуг А1С1В (он же А1С1В1, по условию задачи он прямоуг) .

Видео:№473. Через вершину С треугольника ABC проведена прямая m, параллельная стороне АВ. Докажите,Скачать

Через вершину b треугольника abc проведена прямая параллельная прямой ac

§ 15. Свойства параллельных прямых

(обратная теореме 14.1)

Если две параллельные прямые пересечены секущей, то углы, образующие пару накрест лежащих углов, равны.

На рисунке 224 прямые a и b параллельны, прямая c — секущая. Докажем, что ∠ 1 = ∠ 2.

Пусть ∠ 1 ≠ ∠ 2. Тогда через точку K проведём прямую a 1 так, чтобы ∠ 3 = ∠ 2 (рис. 224). Углы 3 и 2 являются накрест лежащими при прямых a 1 и b и секущей c . Тогда по теореме 14.1 a 1 ‖ b . Получили, что через точку K проходят две прямые, параллельные прямой b . Это противоречит аксиоме параллельности прямых. Таким образом, наше предположение неверно, и, следовательно, ∠ 1 = ∠ 2.

(обратная теореме 14.3)

Если две параллельные прямые пересечены секущей, то углы, образующие пару соответственных углов, равны.

На рисунке 225 прямые a и b параллельны, прямая c — секущая. Докажем, что ∠ 1 = ∠ 2.

По теореме 15.1 углы 3 и 2 равны как накрест лежащие при параллельных прямых a и b и секущей c . Но углы 3 и 1 равны как вертикальные. Следовательно, ∠ 1 = ∠ 2.

(обратная теореме 14.2)

Если две параллельные прямые пересечены секущей, то сумма углов, образующих пару односторонних углов, равна 180° .

На рисунке 226 прямые a и b параллельны, прямая c — секущая. Докажем, что ∠ 1 + ∠ 2 = 180°.

По теореме 15.1 углы 3 и 2 равны как накрест лежащие при параллельных прямых a и b и секущей c . Но углы 3 и 1 смежные, поэтому ∠ 1 + ∠ 3 = 180°. Следовательно, ∠ 1 + ∠ 2 = 180°.

Если прямая перпендикулярна одной из двух параллельных прямых, то она перпендикулярна и другой ( рис. 227 ).

Докажите это следствие самостоятельно.

Задача. Докажите, что все точки одной из двух параллельных прямых равноудалены от другой прямой.

Решение. Пусть прямые a и b параллельны (рис. 228), M и N — две произвольные точки прямой a . Опустим из них перпендикуляры MK и NP на прямую b . Докажем, что MK = NP .

Рассмотрим треугольники MKN и PNK . Отрезок KN — их общая сторона. Так как MK ⊥ b и NP ⊥ b , то MK ‖ NP , а углы MKN и PNK равны как накрест лежащие при параллельных прямых MK и NP и секущей KN .

Аналогично углы MNK и PKN равны как накрест лежащие при параллельных прямых MN и KP и секущей KN . Следовательно, треугольники MKN и PNK равны по стороне и двум прилежащим углам.

Тогда MK = NP .

Расстоянием между двумя параллельными прямыми называют расстояние от любой точки одной из прямых до другой прямой.

Например, на рисунке 228 длина отрезка MK — это расстояние между параллельными прямыми a и b .

Задача. На рисунке 229 отрезок AK — биссектриса треугольника ABC , MK ‖ AC . Докажите, что треугольник AMK — равнобедренный.

Решение. Так как AK — биссектриса треугольника ABC , то ∠ MAK = ∠ KAC .

Углы KAC и MKA равны как накрест лежащие при параллельных прямых MK и AC и секущей AK . Следовательно, ∠ MAK = ∠ MKA .

Тогда треугольник AMK — равнобедренный.

1. Каким свойством обладают накрест лежащие углы, образованные при пересечении двух параллельных прямых секущей?
2. Каким свойством обладают соответственные углы, образованные при пересечении двух параллельных прямых секущей?
3. Чему равна сумма односторонних углов, образованных при пересечении двух параллельных прямых секущей?
4. Известно, что прямая перпендикулярна одной из двух параллельных прямых. Обязательно ли она перпендикулярна другой прямой?
5. Что называют расстоянием между двумя параллельными прямыми?

326. На рисунке 230 найдите угол 1.

327. На рисунке 231 найдите угол 2.

328. Разность односторонних углов, образованных при пересечении двух параллельных прямых секущей, равна 50°. Найдите эти углы.

329. Один из односторонних углов, образованных при пересечении двух параллельных прямых секущей, в 4 раза больше другого. Найдите эти углы.

330. Найдите все углы, образованные при пересечении двух параллельных прямых секущей, если:

1) один из этих углов равен 48°;

2) отношение градусных мер двух из этих углов равно 2 : 7.

331. Найдите все углы, образованные при пересечении двух параллельных прямых секущей, если один из них на 24° меньше другого.

332. На рисунке 232 m ‖ n , p ‖ k , ∠1 = 50°. Найдите ∠ 2, ∠ 3 и ∠ 4.

333. Прямая, параллельная основанию AC равнобедренного треугольника ABC , пересекает его боковые стороны AB и BC в точках D и F соответственно. Докажите, что треугольник DBF — равнобедренный.

334. На продолжениях сторон AC и BC треугольника ABC ( AB = BC ) за точки A и B отметили соответственно точки P и K так, что PK ‖ AB . Докажите, что треугольник KPC — равнобедренный.

335. Отрезки AB и CD пересекаются в точке O , AO = BO , AC ‖ BD . Докажите, что CO = DO .

336. Отрезки MK и DE пересекаются в точке F , DK ‖ ME , DK = ME . Докажите, что ∆ MEF = ∆ DKF .

337. Ответьте на вопросы.

1) Могут ли оба односторонних угла при двух параллельных прямых и секущей быть тупыми?

2) Может ли сумма накрест лежащих углов при двух параллельных прямых и секущей быть равной 180°?

3) Могут ли быть равными односторонние углы при двух параллельных прямых и секущей?

338. На рисунке 233 AB ‖ CD , BC ‖ AD . Докажите, что BC = AD .

339. На рисунке 233 BC = AD , BC ‖ AD . Докажите, что AB ‖ CD .

340. На рисунке 234 MK ‖ EF , ME = EF , ∠ KMF = 70°. Найдите ∠ MEF .

341. Через вершину B треугольника ABC (рис. 235) провели прямую MK , параллельную прямой AC , ∠ MBA = 42°, ∠ CBK = 56°. Найдите углы треугольника ABC .

342. Прямая, проведённая через вершину A треугольника ABC параллельно его противолежащей стороне, образует со стороной AC угол, равный углу BAC . Докажите, что данный треугольник — равнобедренный.

343. На рисунке 236 ∠ MAB = 50°, ∠ ABK = 130°, ∠ ACB = 40°, CE — биссектриса угла ACD . Найдите углы треугольника ACE .

344. На рисунке 237 BE ⊥ AK , CF ⊥ AK , CK — биссектриса угла FCD , ∠ ABE = 32°. Найдите ∠ ACK .

345. На рисунке 238 BC ‖ MK , BK = KE , CK = KD . Докажите, что AD ‖ MK .

346. На рисунке 239 AB = AC , AF = FE , AB ‖ EF . Докажите, что AE ⊥ BC .

347. Треугольник ABC — равнобедренный с основанием AC . Через произвольную точку M его биссектрисы BD проведены прямые, параллельные его сторонам AB и BC и пересекающие отрезок AC в точках E и F соответственно. Докажите, что DE = DF .

348. На рисунке 240 AB ‖ DE . Докажите, что ∠ BCD = ∠ ABC + ∠ CDE .

349. На рисунке 241 AB ‖ DE , ∠ ABC = 120°, ∠ CDE = 150°. Докажите, что BC ⊥ CD .

350. Через вершину B треугольника ABC провели прямую, параллельную его биссектрисе AM . Эта прямая пересекает прямую AC в точке K . Докажите, что ∆ BAK — равнобедренный.

351. Через точку O пересечения биссектрис AE и CF треугольника ABC провели прямую, параллельную прямой AC . Эта прямая пересекает сторону AB в точке M , а сторону BC — в точке K . Докажите, что MK = AM + CK .

352. Биссектрисы углов BAC и BCA треугольника ABC пересекаются в точке O . Через эту точку проведены прямые, параллельные прямым AB и BC и пересекающие сторону AC в точках M и K соответственно. Докажите, что периметр треугольника MOK равен длине стороны AC .

Упражнения для повторения

353. На отрезке AB отметили точку C так, что AC : BC = 2 : 1. На отрезке AC отметили точку D так, что AD : CD = 3 : 2. В каком отношении точка D делит отрезок AB ?

354. Отрезки AC и BD пересекаются в точке O , AB = BC = CD = AD . Докажите, что AC ⊥ BD .

355. В треугольнике MOE на стороне MO отметили точку A , в треугольнике TPK на стороне TP — точку B так, что MA = TB . Какова градусная мера угла BKP , если MO = TP , ∠ M = ∠ T , ∠ O = ∠ P , ∠ AEO = 17°?

Наблюдайте, рисуйте, конструируйте, фантазируйте

356. На рисунке 242 изображена очень сложная замкнутая ломаная. Она ограничивает некоторую часть плоскости (многоугольник). Как, отметив на рисунке любую точку, по возможности быстрее определить, принадлежит эта точка многоугольнику или нет?

Видео:№243. Через вершину С треугольника ABC проведена прямая, параллельная его биссектрисе АА1Скачать

В треугольнике ABM через вершину В проведена прямая D, параллельная стороне АM?

Математика | 5 — 9 классы

В треугольнике ABM через вершину В проведена прямая D, параллельная стороне АM.

Из вершин А и М проведены перпендикуляры АС и МD на прямую D.

Найдите площадь четырехугольника АСDМ, если площадь треугольника ABM равна 23 см в кв

Решение : здесь речь идёт о площади прямоугольника.

Видео:№245. Через точку пересечения биссектрис ВВ1 и СС1 треугольника ABC проведена прямая, параллельнаяСкачать

Через середину К медианы ВМ треугольника АВС и вершину А проведена прямая, пересекающая сторону ВС в точке Р?

Через середину К медианы ВМ треугольника АВС и вершину А проведена прямая, пересекающая сторону ВС в точке Р.

Найдите отношение площади треугольника АВК к площади четырехугольника КРСМ.

ПОЖАЛУЙСТА ПОМОГИТЕ У МЕНЯ ЭКЗАМЕН.

Видео:№384. Через середину М стороны АВ треугольника ABC проведена прямая,Скачать

Через вершину с треугольника авс проведена прямая параллельная биссектрисе AM треугольника и пересекающая прямую AB в точке K?

Через вершину с треугольника авс проведена прямая параллельная биссектрисе AM треугольника и пересекающая прямую AB в точке K.

Найдите углы треугольника AKC если угол BAC = 70.

Видео:№563. Через точку М, взятую на медиане AD треугольника ABC, и вершину В проведена прямая,Скачать

В равнобедренном прямоугольном треугольнике медиана, проведенная из вершины прямого угла, равна 5 см?

В равнобедренном прямоугольном треугольнике медиана, проведенная из вершины прямого угла, равна 5 см.

Найдите площадь треугольника.

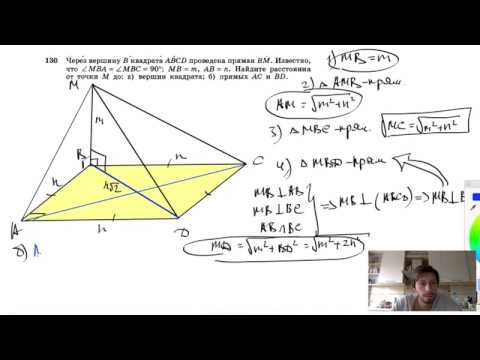
Видео:№130. Через вершину В квадрата ABCD проведена прямая ВМ. Известно, что ∠MBA = ∠MBC=90°, МВ =m, АВСкачать

В равнобедренном треугольнике ABC с вершиной B проведена медиана AM к боковой стороне?

В равнобедренном треугольнике ABC с вершиной B проведена медиана AM к боковой стороне.

Найдите квадрат радиуса окружности, описанной около треугольника ABC, если радиусы окружностей, описанных около треугольников ABM и AMC, равны соответственно 36 и 9.

Видео:№152. Через вершину В квадрата ABCD проведена прямая BF, перпендикулярная к его плоскости. НайдитеСкачать

Дан треугольник АВС?

Дан треугольник АВС.

Через вершину А проведите прямую, параллельную стороне ВС, через вершину В — прямую, параллельную стороне АС, через вершину С — прямую параллельную стороне АВ.

Сколько треугольников получилось?

Пожалуйста можно с рисунком!

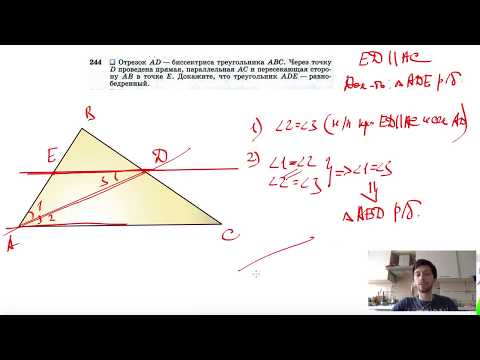
Видео:№244. Отрезок AD — биссектриса треугольника ABC. Через точку D проведена прямая, параллельная АССкачать

Через середину К медианы BM треугольника АБС и вершину А проведена прямая, пересекающая сторону ВС в точкее Р?

Через середину К медианы BM треугольника АБС и вершину А проведена прямая, пересекающая сторону ВС в точкее Р.

Найдите отношение площади треугольника АВК к площади четырехугольника КРСМ.

Видео:№145. Через вершину А прямоугольного треугольника ABC с прямым углом С проведена прямая AD,Скачать

В треугольнике проведена высота из вершины прямого угла Докажите что данный треугольник из — за образовавшейся треугольника имеют соответственно равные углы?

В треугольнике проведена высота из вершины прямого угла Докажите что данный треугольник из — за образовавшейся треугольника имеют соответственно равные углы.

Видео:Геометрия Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точкахСкачать

Постройте произвольный треугольник ?

Постройте произвольный треугольник .

Через его вершины проведите прямые , параллельные сторонам треугольника .

Сравните углы треугольника , образованного построенными прямыми , и треугольника.

Видео:№158. Через вершину В ромба ABCD проведена прямая ВМ, перпендикулярная к его плоскости. НайдитеСкачать

В прямоугольнике ABCD проведена биссектриса AM?

В прямоугольнике ABCD проведена биссектриса AM.

Периметр прямоугольника равен 80 см.

Найдите сторону AD, если площадь треугольника ABM равна 162 см.

Видео:№205. Через вершину С прямого угла прямоугольного треугольника ABC проведена прямая CD, перпендикуляСкачать

Дан треугольник ABC?

Дан треугольник ABC.

Через вершину А проведите прямую, параллельную стороне ВС, через вершину В — прямую, параллельную стороне АС, через вершинуи С — прямую, параллельную стороне АВ.

Сколько попарно параллельных отрезков получилось?

Сколько треугольников получилось?

Вы находитесь на странице вопроса В треугольнике ABM через вершину В проведена прямая D, параллельная стороне АM? из категории Математика. Уровень сложности вопроса рассчитан на учащихся 5 — 9 классов. На странице можно узнать правильный ответ, сверить его со своим вариантом и обсудить возможные версии с другими пользователями сайта посредством обратной связи. Если ответ вызывает сомнения или покажется вам неполным, для проверки найдите ответы на аналогичные вопросы по теме в этой же категории, или создайте новый вопрос, используя ключевые слова: введите вопрос в поисковую строку, нажав кнопку в верхней части страницы.

🔍 Видео

№155. Через вершину прямого угла С равнобедренного прямоугольного треугольника ABCСкачать

№150. Через вершину А прямоугольника ABCD проведена прямая АК, перпендикулярная к плоскостиСкачать

№38. Через вершину А ромба ABCD проведена прямая а, параллельная диагонали BD,Скачать

№199. Прямая р параллельна стороне АВ треугольника ABC. Докажите, что прямые ВССкачать

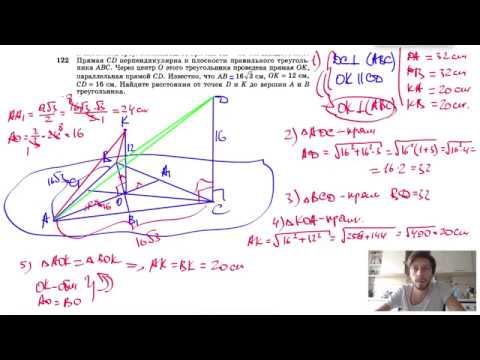
№122. Прямая CD перпендикулярна к плоскости правильного треугольника ABC. Через центр О этогоСкачать

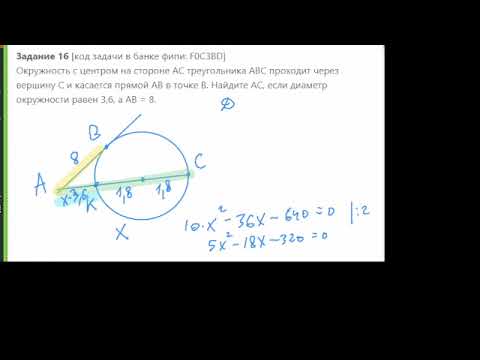
Окружность с центром на стороне AС треугольника ABC проходит через вершину С и касается прямой AB вСкачать

№193. В треугольнике ABC ∠A=40°, ∠B=70°. Через вершину B проведена прямая BD так, что луч ВССкачать

Через середину К медианы ВМ треугольника АВС и вершину А проведена прямая пересекающая сторону ВС вСкачать