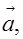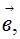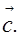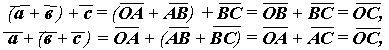Курсовая работа по теме векторы

1. Что такое вектор?

2. Сложение векторов.

3. Равенство векторов.

4. Скалярное произведение двух векторов и его свойства.

5. Свойства операций над векторами.

6. Доказательства и решение задач.

Одним из фундаментальных понятий современной математики являются вектор и его обобщение – тензор. Эволюция понятия вектора осуществлялась благодаря широкому использованию этого понятия в различных областях математики, механики, а так же в технике.

Конец прошлого и начало текущего столетия ознаменовались широким развитием векторного исчисления и его приложений. Были созданы векторная алгебра и векторный анализ, общая теория векторного пространства. Эти теории были использованы при построении специальной и общей теории относительности, которые играют исключительно важную роль в современной физике.

В соответствии с требованиями новой программы по математике понятие вектора стало одним из ведущих понятий школьного курса математики.

Что же такое вектор? Как ни странно, ответ на этот вопрос представляет известные затруднения. Существуют различные подходы к определению понятия вектора; при этом даже если ограничиться лишь наиболее интересным здесь для нас элементарно-геометрическим подходом к понятию вектора, то и тогда будут иметься различные взгляды на это понятие. Разумеется, какое бы определение мы ни взяли, вектор – с элементарно-геометрической точки зрения — есть геометрический объект, характеризуемый направлением ( т.е. заданной с точностью до параллельности прямой и направлением на ней) и длиной.Однако такое определение является слишком общим, не вызывающим конкретных геометрических представлений. Согласно этому общему определению параллельный перенос можно считать вектором. И действительно, можно было бы принять такое определение: “Вектором называется всякий параллельный перенос”. Это определение логически безупречно, и на его основе может быть построена вся теория действий над векторами и развиты приложения этой теории. Однако это определение, несмотря на его полную конкретность , нас здесь также не может удовлетворить, так как представление о векторе как о геометрическом преобразовании кажется нам недостаточно наглядным и далеким от физических представлений о векторных величинах.

Итак, вектором называется семейство всех параллельных между собой одинаково направленных и имеющих одинаковую длину отрезков (рис.1).

Вектор изображают на чертежах отрезком со стрелкой (т.е. изображают не все семейство отрезков, представляющее собой вектор, а лишь один из этих отрезков). Для обозначения векторов в книгах и статьях применяют жирные латинские буквы а, в, с и так далее, а в тетрадях и на доске – латинские буквы с черточкой сверху,

Той же буквой, но не жирной , а светлой (а в тетради и на доске- той же буквой без черточки) обозначают длину вектора. Длину иногда обозначают также вертикальными черточками – как модуль (абсолютную величину) числа. Таким образом, длина вектора а обозначается через а или Iа I, а в рукописном тексте длина вектора а обозначается через а или Iа I. В связи с изображением векторов в виде отрезков (рис.2) следует помнить , что концы отрезка, изображающего вектор, неравноправны: одного конца отрезка к другому.

Различают начало и конец вектора (точнее, отрезка, изображающего вектор).

Весьма часто понятию вектора дается другое определение:вектором называется направленный отрезок. При этом векторы (т.е. направленные отрезки), имеющие одинаковую длину и одно и то же направление (рис.3), уславливаются считать равными.

Векторы называются одинаково направленными, если их полупрямые одинаково направлены.

Все сказанное пока еще не дает понятие вектора достаточно содержательным и полезным. Большую содержательность и богатую возможность приложений понятие вектора получает тогда, когда мы вводим своеобразную “геометрическую арифметику” – арифметику векторов, позволяющую складывать векторы, вычитать их и производить над ними целый ряд других операций. Отметим в связи с этим, что ведь и понятие числа становится интересным лишь при введении арифметических действий, а не само по себе.

Суммой векторов а и в с координатами а₁ , а₂ и в₁ , в₂ называется вектор с с координатами а₁ + в₁ , а₂ + в₂ , т.е.

а (а₁ ; а₂ ) + в (в₁ ;в₂ ) = с (а₁ + в₁ ; а₂ + в₂ ).

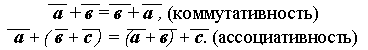Следствие:

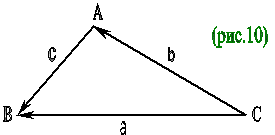
Для доказательства коммутативности сложения векторов на плоскости необходимо рассмотреть пример.

а и в – векторы (рис.5).

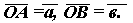Пусть

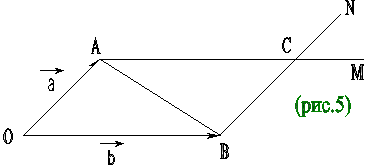
1. Строим параллелограмм ОАСВ: АМ II ОВ, ВН II ОА.

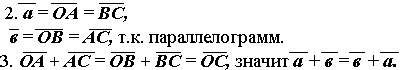
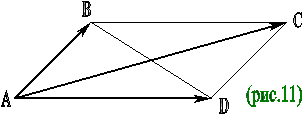
Для доказательства ассоциативности мы отложим от произвольной точки О вектор ОА = а, от точки А вектор АВ = в и от точки в – вектор ВС = с. Тогда мы имеем:АВ + ВС =АС.

откуда и следует равенство а + ( в + с ) = (а + в ) + с. Заметим, что приведенное доказательство совсем не использует чертежа. Это характерно ( при некотором навыке ) для решения задач при помощи векторов.

Остановимся теперь на случае, когда векторы а и в направлены в противоположные стороны и имеют равные длины; такие векторы называют противоположными. Наше правило сложения векторов приводит к тому, что сумма двух противоположных векторов представляет собой “вектор”, имеющий нулевую длину и не имеющий никакого направления; этот “вектор” изображается “отрезком нулевой длины”, т.е. точкой. Но это тоже вектор, который называется нулевым и обозначается символом 0.

Два вектора называются равными, если они совмещаются параллельным переносом. Это означает, что существует параллельный перенос, который переводит начало и конец одного вектора соответственно в начало и конец другого вектора.

Из данного определения равенства векторов следует, что разные векторы одинаково направлены и равны по абсолютной величине.

И обратно: если векторы одинаково направлены и равны по абсолютной величине, то они равны.

Действительно, пусть векторы АВ и С D – одинаково направленные векторы, равные по абсолютной величине (рис.6). Параллельный перенос, переводящий точку С в точку А, совмещает полупрямую СD с полупрямой АВ, так как они одинаково направлены. А так как отрезки АВ и CD равны, то при этом точка D совмещается с точкой В, то есть параллельный перенос переводит вектор CD в вектор АВ. Значит, векторы АВ и С D равны, что и требовалось доказать.

Скалярное произведение двух векторов и его свойства.

Скалярным произведением двух нулевых векторов называется число, равное произведению числовых значений длин этих векторов на косинус угла между векторами.

Обозначение: а х в = Ia I * Ib I * cos ( а, в ).

Свойства скалярного произведения:

1. а х в = в х а.

2. Для того, чтобы два нулевых вектора а и в были перпендикулярны, необходимо и достаточно, чтобы скалярное произведение этих векторов было равно нулю, т.е. а х в = 0.

3. Выражение а х а будем обозначать а 2 и называть скалярным квадратом вектора а .

Свойства операций над векторами.

Имеют место следующие теоремы об операциях над векторами, заданными в координатной форме.

1. Пусть даны а = (а_х , а _y , а _z ) и в = ( в _x , в_у , в _z ) , тогда сумма этих векторов есть вектор с , координаты которого равны сумме одноименных координат слагаемых векторов, т.е. с = а + в = (а_х + в _x ; а _y + в_у ; а _z + в _z ).

Пример 1.

а = ( 3; 4; 6) и в = ( -1; 4; -3), тогда с = ( 3 + ( -1); 4 + 4; 6 + (-3)) = ( 2; 8; 3).

2. а = (а_х , а _y , а _z ) и в = ( в _x , в_у , в _z ) , тогда разность этих векторов есть вектор с , координаты которого равны разности одноименных координат данных векторов, т.е. с = а — в = (а_х — в _x ; а _y — в_у ; а _z — в _z ).

а = ( -2; 8; -3) и в = ( -4; -5; 0), тогда с = а – в = ( -2 – ( -4 ); 8 – ( -5 ); -3 –0 ) = ( 2; -13; -3).

3. При умножении вектора а = (а_х , а _y , а _z ) на число м все его координаты умножаются на это число, т.е. ма = ( ма_х , ма _y , ма _z ).

Пример 3.

а = ( -8; 4; 0) и м = 3, тогда 3а = ( -8 х 3; 4 х 3; 0 х 3) = ( -24; 12; 0).

Понятие вектора, которое нашло широкое распространение в прикладных науках, явилось плодотворным и в геометрии. Аппарат векторной алгебры позволил упростить изложение некоторых сложных геометрических понятий, доказательства некоторых теорем школьного курса геометрии, позволил создать особый метод решения различных геометрических задач.

Рассмотрим доказательство некоторых теорем с помощью векторов.

Диагонали ромба взаимно перпендикулярны.

Пусть АВСD – данный ромб (рис.7). Введем обозначения: АВ = а , ВС = в . Из определения ромба: АВ = DC = а , AD = ВС = в.

По определению суммы и разности векторов АС = а + в; DВ = а – в.

Рассмотрим АС * DВ = (а + в )( а – в ) = а 2 – в 2 .

Так как стороны ромба равны, то а = в . Следовательно, AC * DB =0. Из последнего получаем

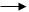
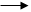
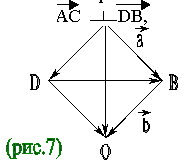Рассмотрим теперь решение задач с помощью векторов.

Даны два вектора AB и CD, причем А( -1; 2; 4), В ( -4; 5; 4), С( -1; -2; 2) и D(2; 1;5).

Определить, перпендикулярны они друг другу или нет.

Найдем сначала координаты векторов. АВ = ( -3; 3; 0) и СD = (3; 3; 3).

Вычислим теперь скалярное произведение этих векторов:

АВ х СD = ( -3) х 3 + 3 х 3 + 0 х 3 = 0.

Последнее и означает, что АВ СD.

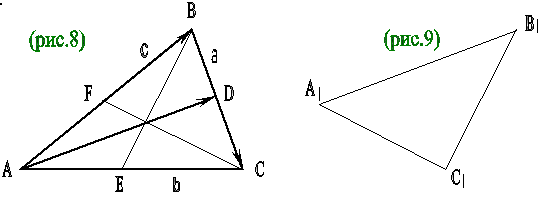
Дан произвольный треугольник АВС. Доказать, что можно построить треугольник, стороны которого равны и параллельны медианам треугольника АВС.

Обозначим медианы треугольника АВС через ВЕ, СF и обозначим векторы, идущие вдоль сторон треугольника АВС, через а, в, с :

ВС = а, СА = в, АВ = с

АD = АВ + ВD = АВ += с +

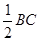
аналогично определяются и другие медианы:

ВЕ = а + , СF = в +

Так как, в силу условия замкнутости

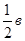
ВС + СА + АВ = а + в + с = 0,

АD + ВЕ + СF = ( с + ) + (а + ) + ( в + ) = ( а + в + с ) = х 0 = 0.

Следовательно, отложив от точки В, вектор В₁ С₁ = ВЕ и от точки С₁ – вектор С₁ D₁ = СF, мы получим.

А₁ В₁ + В₁ С₁ + С₁ D₁ = АD + ВЕ + СF = 0.

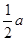
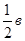
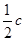
А это значит (в силу условия замкнутости), что ломаная А₁ В₁ С₁ D₁ является замкнутой, т.е. точка D₁ совпадает с А₁ .

Таким образом, мы получаем треугольник А₁ В₁ С₁ (рис.9), стороны которого равны и параллельны медианам АD, ВЕ, СF исходного треугольника.

Доказать, что для любого треугольника имеет место формула

с 2 = а 2 + в 2 – 2ав х соs С (теорема косинусов)

Решение.

Положим: а = СВ, в = СА,

Тогда с = а – в , и мы имеем

(учитывая, что угол между векторами а и в равен С):

с 2 = ( а – в ) 2 = а 2 – 2ав + в 2 = а 2 – 2ав х соs С + в 2 .

Докажите, что сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон.

Пусть четырехугольник АВСD – параллелограмм (рис.11). Имеем векторные равенства

АВ + AD = АС, АВ – АD = DВ.

Возведем эти равенства в квадрат. Получим:

АВ 2 + 2 АВ х АD + АD 2 = АС 2 , АВ 2 – 2АВ х АD + АD 2 = DВ 2

Сложим эти равенства почленно. Получим:

2АВ 2 + 2 АD 2 = АС 2 + DВ 2 .

Так как у параллелограмма противолежащие стороны равны, то это равенство и означает, что сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон, что и требовалось доказать.

Даны три точки: А ( 1; 1), В ( -1; 0), С ( 0; 1). найдите такую точку D ( х; y ), чтобы векторы АВ и СD были равны.

Вектор АВ имеет координаты –2, -1. Вектор СD имеет координаты х – 0, y – 1. Так как АВ = СD, то х – 0 = -2, y – 1 = -1. Отсюда находим координаты точки D: х = -2, y = 0.

Даны два вектора АВ и СD, причем А ( -1; 2; 4), В ( -4; 5; 4), С ( -1; -2; 2), D ( 2; 1; 5).Определить, перпендикулярны они друг другу или нет.

Решение.

Найдем сначала координаты векторов. АВ = ( -3; 3; 0) и СD ( 3; 3; 3).

Вычислим теперь скалярное произведение этих векторов:

AB х CD = ( -3) х 3 + 3 х 3 + 0 х 3 = 0.

Последнее озночает, что АВ СD.

Рассмотренные выше примеры задач показывают, что векторный метод является весьма мощных средством решения геометрических и многих физических (и технических) задач.

1. “Векторы в школьном курсе геометрии”. (1976г.) В.А.Гусев. Ю.М.Колягин. Г.Л.Луканкин.

2. “Векторы в курсе геометрии средней школы. (1962г.) В.Г.Болтянский. И.М.Яглом.

Видео:ПРОСТОЙ СПОСОБ, как запомнить Векторы за 10 минут! (вы будете в шоке)Скачать

Векторы на плоскости и в пространстве

Видео:РАЗБОР КОНТРОЛЬНОЙ РАБОТЫ | 9 КЛАСС ГЕОМЕТРИЯ АТАНАСЯН | ВЕКТОРЫСкачать

Пример курсовой работы

Содержание

ВВЕДЕНИЕ 2
1. Направленные отрезки 4
2. Векторы 7
3. Сложение и вычитание векторов 11
4. Умножение вектора на число 15
5. Линейная зависимость векторов 18
6. Скалярное,векторное и смешанное произведения векторов 22
7. Применение векторов к решению задач. 24
Заключение 26
ЛИТЕРАТУРА 27

Введение

Одним из фундаментальных понятий современной математики являются вектор и его обобщение – тензор. Эволюция понятия вектора осуществлялась благодаря широкому использованию этого понятия в различных областях математики, механики, а так же в технике.
Конец прошлого и начало текущего столетия ознаменовались широким развитием векторного исчисления и его приложений. Были созданы векторная алгебра и векторный анализ, общая теория векторного пространства. Эти теории были использованы при построении специальной и общей теории относительности, которые играют исключительно важную роль в современной физике. [3]
В соответствии с требованиями новой программы по математике понятие вектора стало одним из ведущих понятий школьного курса математики.
Существуют различные подходы к определению понятия вектора; при этом даже если ограничиться лишь наиболее интересным здесь для нас элементарно-геометрическим подходом к понятию вектора, то и тогда будут иметься различные взгляды на это понятие. Разумеется, какое бы определение мы ни взяли, вектор – с элементарно-геометрической точки зрения — есть геометрический объект, характеризуемый направлением (т.е. заданной с точностью до параллельности прямой и направлением на ней) и длиной. Однако такое определение является слишком общим, не вызывающим конкретных геометрических представлений. Согласно этому общему определению параллельный перенос можно считать вектором. И действительно, можно было бы принять такое определение: “Вектором называется всякий параллельный перенос”. Это определение логически безупречно, и на его основе может быть построена вся теория действий над векторами и развиты приложения этой теории. Однако это определение, несмотря на его полную конкретность, нас здесь также не может удовлетворить, так как представление о векторе как о геометрическом преобразовании кажется нам недостаточно наглядным и далеким от физических представлений о векторных величинах.
Целью данной работы является рассмотреть векторы на плоскости и пространстве.
Реализации данной цели служит ряд задач:
1. Рассмотреть направленные отрезки.
2. Дать понятие вектора.
3. Рассмотреть сложение и вычитание векторов, умножение вектора на число.
4. Рассмотреть линейную зависимость векторов.
5. Изучить скалярное, векторное и смешанное произведение векторов

Список использованных источников

1. Александров А.Д. Геометрия//Математический энциклопедический словарь. — М.: «Большая российская энциклопедия», 1995.
2. Александров А.Д., Нецветаев Н.Ю. Геометрия.- М.: Наука,1990.
3. Александров П.С. Курс аналитической геометрии и линейной алгебры. М., Наука, 1979.
4. Артин Э. Геометрическая алгебра. М., Мир, 1970.
5. Атанасян Л. С., Базылев В. Т. Геометрия. Ч. 1, 2 – М.: Просвещение, 1986.
6. Беклемишев Д.В. Курс аналитической геометрии и линейной алгебры. М., Наука, 2003.
7. Борисенко А. И., Тарапов И. Е. Векторный анализ и начала тензорного исчисления. – Минск: Высшая школа, 1966.
8. Ван де Варден Б.Л. Алгебра. – М., Наука, 1976.
9. Вейль Г. Классические группы, их инварианты и представления. – М.: Иностранная литература, 1947.
10. Вейль Г. Математическое мышление. — М.:Наука,1989.
11. Воеводин В.В. Вычислительные основы линейной алгебры. М., Наука, 1977.
12. Гельфанд И.М. Лекции по линейной алгебре. М., Наука, 1966.
13. Глазман И.М., Любич Ю.И. Конечномерный линейный анализ. М., Наука, 1969.
14. Головина Л.И. Линейная алгебра и некоторые ее приложения. — М.: Наука, 1985.
15. Ефимов Н. В, Розендорн Э.Р. Линейная алгебра и многомерная геометрия. — М.: Наука 1974.
16. Ефимов Н. В. Высшая геометрия. — М.: Наука, 1978.
17. Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. – М.: Наука, 1984.
18. Кострикин А.И. Введение в алгебру. М., Наука, 1977.
19. Кострикин А.И., Манин Ю.И. Линейная алгебра и геометрия. – М.: Изд-во МГУ, 1980.
20. Кочин Н. Е. Векторное исчисление и начала тензорного исчисления. – М.: Наука, 1965.
21. Курош А.Г. Курс высшей алгебры. – М., Наука, 1975.
22. Мальцев А.Н. Основы линейной алгебры. М., Наука, 1970.
23. Математика в понятиях, определениях и терминах. Ч.1,2. – М.: Просвещение, 1982.
24. Минковский Г. Пространство и время. — В кн.: Принцип относительности. — М., Атомиздат,1973.
25. Постников М. М. Аналитическая геометрия. – М.: Наука, 1986.
26. Тышкевич Р. И., Феденко А. С. Линейная алгебра и аналитическая геометрия. – Минск: Высшая школа, 1968.
27. Философский энциклопедический словарь. — Москва: Советская энциклопедия, 1983.
28. Халмош П.Р. Конечномерные векторные пространства. М., Физматгиз, 1963.
29. Чехлов В.И. Лекции по аналитической геометрии и линейной алгебре. – М.: МФТИ, 2000.

Видео:9 кл Геометрия КР№1 ВекторыСкачать

КУРСОВАЯ РАБОТА тема Векторы в курсе математики 9-го класса

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Видео:ВЕКТОРЫ. Контрольная № 4 Геометрия 9 класс.Скачать

«Снятие эмоционального напряжения
у детей и подростков с помощью арт-практик
и психологических упражнений»

Сертификат и скидка на обучение каждому участнику

Министерство образования и науки Республики Дагестан

Негосударственная автономная некоммерческая организация дополнительного профессионального образования

«Дагестанский институт экономики и политики»

Кафедра Методики Преподавания Математики

«Векторы в курсе математики 9-го класса»

Учитель первой квалификационной категории

ГКОУ РД «Кикуникутанская ООШ Гергебильского района»

Расулов Хайрула Рамазанович

1 глава. Понятие вектора в школьном курсе геометрии 4

§1 Место изучения понятия вектор и действий над векторами 4

2 глава. Векторы на плоскости 7

§1 Основные определения 7

§2 Коллинеарные векторы 8

§3 Равенство векторов 9

§4 Координаты вектора 10

§5 Сложение и вычитание векторов 12

§7 Умножение вектора на число 14

§8 Разложение вектора по двум неколлинеарным векторам 16

§9 Скалярное произведение векторов 16

§10 Разложение вектора по координатным осям 19

Набор упражнений для самостоятельного решения учащимися 21

Список использованных источников 22

Видео:Геометрия 9. Подготовка к КР по теме ВекторыСкачать

Введение

В настоящее время проблемам преподавания математики в школе стали уделять больше внимания. Это связано с научно-техническим прогрессом и развитием наукоемких производств. Технические науки, среди которых, в последнее время, быстро развиваются и имеют огромное практическое значение, такие как информационные технологии, электроника и т.д., немыслимы без математического аппарата.

Основа для математической грамотности закладывается именно в школе, поэтому изучению вопросов, связанных с этим процессом, уделяется пристальное внимание. Математика является одним из опорных предметов школы. Она требует от учащихся волевых и умственных усилий, развитого воображения, концентрации внимания. Математика развивает личность учащегося. Изучение математики существенно способствует развитию логического мышления и расширяет кругозор школьников.

Кроме всего вышесказанного, математика обеспечивает изучение других школьных дисциплин, таких как физика, химия и др. На уроках математики учащиеся получают не только вычислительные навыки для решения прикладных задач, но и узнают такие необходимые для решения, например, физических задач понятия, как: вектор и действия над векторами, аффинная система координат, начинают решать задачи с использованием координатного метода и т.п.

Задачи данной работы: рассмотреть понятие вектора на плоскости, показать действия над векторами, разобрать методы решение геометрических задач с использованием основных векторных соотношений . В работе будут рассмотрены и изучены: печатные учебные пособия для учащихся, используемые в настоящее время в общеобразовательных средних школах; различные учебные пособия по данной теме; электронные учебные пособия и проекты в сети интернет.

Видео:Координаты вектора. 9 класс.Скачать

1 глава.
Понятие вектора в школьном курсе геометрии

Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

§1 Место изучения понятия вектор и действий над векторами

Материалу, непосредственно связанному с изучением векторов на плоскости, отводится достаточно немного времени в школьной программе по математике. Хотя, стоит заметить, что курс геометрии в старших классах средней школы строится именно на основе векторных представлений. Данный материал играет важную роль при решении школьниками многих геометрических и физических задач, закладывает основу для изучения понятия вектора в пространстве.

Изучение векторов начинается в четвертой четверти VIII класса. Для успешного освоения учащимися данного материала, они должны быть знакомы с понятием декартовых координат на плоскости, понятием отрезок, уметь определять координаты на плоскости и расстояние между двумя точками на плоскости, а также понимать значение понятия параллельный перенос и знать его свойства.

В учебнике Погорелова А.В. [4], который сейчас в основном используется в школах, материал преподносится учащимся в следующем порядке:

1) Даются основные понятия: вектор, направление вектора, абсолютная величина (модуль), нулевой вектор.

2) Рассматривается понятие равенства векторов.

3) Определяются координаты вектора.

4) Рассматриваются действия над векторами: сложение (вычитание) векторов, умножение вектора на число. Разбирается, как применяются вектора в физических задачах, на примере сложения сил.

5) Дается понятие коллинеарных векторов и рассматривается разложения вектора по двум неколлинеарным векторам.

6) Рассматривается понятие скалярного произведения векторов.

7) Дается понятия единичного вектора, координатного вектора (орта) и рассматривается разложение вектора по координатным осям.

§2 Основные результаты изучения векторов на плоскости

Прочное освоение в 9 классе материалов, связанных с векторами на плоскости является важным моментом в изучении геометрии, как мы указывали это ранее. Перед преподавателем ставится цель закрепить следующие знания и навыки у учащихся.

1) Учащиеся должны знать:

— основные понятия: вектор, направление вектора, модуль вектора, нулевой вектор, равенства векторов;

— как определяются координаты вектора;

— как выполняются действия над векторами: сложение (вычитание) векторов, умножение вектора на число и какие свойства имеют место при выполнении этих действий;

— понятие коллинеарных векторов;

— понятие скалярного произведения векторов и свойства, которыми обладает скалярное произведение векторов;

— понятия единичного вектора и координатного вектора.

2) Учащиеся должны уметь:

— строить вектор в декартовой системе координат;

— находить модуль вектора;

— находить и записывать координаты вектора;

— выполнять сложение и вычитание векторов графическими методами по «правилу треугольника» и «правилу параллелограмма», а также выполнять эти действия, используя координаты векторов;

— выполнять умножение вектора на число;

— находить скалярное произведение векторов;

— находить разложение вектора по двум неколлинеарных векторам;

— находить разложение вектора по координатным осям;

— решать геометрические задачи, в которых используются основные понятия, связанные с вектором на плоскости, и применять полученные знания о действиях над векторами.

Видео:ВЕКТОРЫ 9 класс С НУЛЯ | Математика ОГЭ 2023 | УмскулСкачать

2 глава.
Векторы на плоскости

Методика обучения математики устанавливает, какими способами можно добиться у всех учащихся прочных знаний, умений и навыков, затрачивая на это минимум сил и времени, а также как развивать творческие способности учащихся и достигать всех тех учебно-воспитательных целей, которые ставятся при изучении математики. Для решения этих задач в методике математики разрабатывают систему методов и приемов обучения.

При использовании различных приемов и методик следует учитывать уровень подготовки учащихся, специфику изучаемой темы и т.п. факторы. Используя в своей работе совокупность различных методов, приемов и их комбинации, учитель может добиться желаемых успехов.

Для более глубокого понимания сути вопроса и возможности подбора необходимых методик преподавания изучаемой нами темы, в данной работе мы рассмотрим содержание основной части школьной программы связанной с этим вопросом.

Видео:Координаты вектора в пространстве. 11 класс.Скачать

§1 Основные определения

В различной литературе понятие вектор вводится по-разному. Так в учебнике Погорелова А.В. [4] дается следующее определение:

«Вектором мы будем называть направленный отрезок (рис. 1). Направление вектора определяется указанием его начала и конца. На чертеже направление вектора отмечается стрелкой.»

В пособие Герасимовича А.И. [1] можно увидеть другой подход во введении этого понятия:

«Величина, которая определяется числовым значением и направлением, называется вектором . Примерами векторов являются сила, скорость, момент силы и др. Геометрической интерпретацией векторов служат направленные отрезки.»

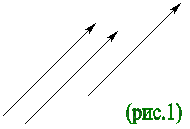
Для обозначения векторов обычно используются строчные латинские буквы: а, b, с и т.д. Кроме этого, обозначить вектор можно указанием его начала и конца (причем, начало вектора указывается первым). Вместо слова “вектор” над буквенным обозначением вектора обычно ставят стрелку или черту. Изображенный на рисунке 1 вектор можно обозначить как: , или , . “ Абсолютной величиной (или модулем ) вектора называется длина отрезка, изображающего вектор.” [4] Абсолютную величину вектора иногда называют, также, длиной вектора и обозначают: или .

Если начало вектора совпадает с его концом, то такой вектор называют нулевым вектором. Такой вектор обозначают . Длина нулевого вектора равна нулю и он не имеет определенного направления.

Видео:Математика это не ИсламСкачать

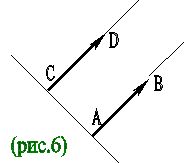
§2 Коллинеарные векторы

“ Два вектора называются колли­неар­ны­ми, если они лежат на параллельных пря­­мых или на одной прямой.” [1, 4]

Коллинеарные векторы могут быть одинаково направлены или проти­вопо­лож­но направлены . Можно по-разному разъяс­нить эти понятия:

1) Расположим два коллинеарных вектора таким образом, чтобы их начала лежали на одной прямой. Если они оба лежат в одной полуплоскости от­но­си­тельно прямой, то векторы одинаково направлены. Если они лежат в разных полуплоскостях относительно прямой, то векторы противоположно нап­равлены.

2) Векторы и называются одинаково направленными, если полупрямые АВ и CD одинаково направлены. Векторы и называются противоположно направленными, если полупрямые АВ и CD противоположно направлены.

3) Если два вектора лежат на одной прямой, они одинаково направлены в том случае, если их направления совпадают с направлением одной из полупрямых данной прямой, и противоположно направлены, если их направления не совпадают с направлением одной полупрямой.

На рисунке 2 векторы и одинаково направлены, а векторы и противоположно направлены. Одинаково направленные векторы принято обозначать ­­ , противоположно направленные – ­¯ .

Видео:18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать

§3 Равенство векторов

“ Два вектора называются равными , если они одинаково направлены и имеют равные длины.” [1] Такое определение дается в пособии Герасимовича А.И.

В учебнике Погорелова А.В. [4] определение дается через понятие параллельного переноса: “Два вектора называются равными, если они совмещаются параллельным переносом. Это означает, что существует параллельный перенос, который переводит начало и конец одного вектора, соответственно в начало и конец другого вектора.

Из данного определения равенства векторов следует, что равные векторы одинаково направлены и равны по абсолютной величине.

Обратно: если векторы одинаково направлены и равны по абсолютной величине, то они равны.”

Рассмотрим наглядно. На рисунке 3 изображены векторы и одинаково направленные и равные по модулю. При параллельном переносе точка С переходит в точку А , совмещая, таким образом, полупрямую CD с полупрямой АВ , так как они одинаково направлены (а соответственно и коллинеарны). Так как векторы равны, то при осуществляемом нами параллельном переносе точка D совмещается с точкой В , а следовательно вектор переходит . Следовательно, векторы и равны, что и требовалось доказать.

Видео:Геометрия - 9 класс (Урок№1 - Понятие вектора. Равенство векторов)Скачать

§4 Координаты вектора

Пусть вектор имеет началом точку А ₁ ( х ₁ ; у ₁ ), а концом точку А ₂ ( х ₂ ; у ₂ ) (см. рисунок 4).

Координатами вектора будем называть числа а ₁ = х ₂ — х ₁ , а ₂ = у ₂ — у ₁ . Принято записывать ( а ₁ ; а ₂ ) или просто . Координаты нулевого вектора равны нулю.

Применив формулу, выражающую рас­стояние между двумя точками по их координатам, выводится формула определения абсолютной величины (модуля) вектора с координатами а ₁ и а ₂ , которая будет равна .

Теорема. Равные векторы имеют равные соответствующие координаты. Обратная: если у векторов соответствующие координаты равны, то векторы равны.

Данную теорему и обратную ей можно доказать двумя способами.

Доказательство 1. Пусть А ₁ ( х ₁ ; у ₁ ) и А ₂ ( х ₂ ; у ₂ ) – начало и конец вектора . Так как равный ему вектор получается из вектора параллельным переносом, то его началом и концом будут соответственно , . Отсюда видно, что оба вектора и имеют одни и те же координаты: х ₁ — х ₂ , у ₁ — у ₂ .

Обратное утверждение доказывается следующим образом. Пусть соответствующие координаты векторов и равны. Докажем, что векторы равны.

Пусть и — координаты точки , а и — координаты точки . По условию теоремы: , . Отсюда , . Параллельный перенос, заданный формулами

, ,

переводит точку А ₁ в точку , а точку А ₂ в точку , т.е. векторы и равны, что и требовалось доказать.

Доказательство 2. Пусть векторы и равны. Это значит, что они имеют одинаковые направления и равные длины: (см. рисунок 4). прямоугольные треугольники А ₁ А ₂ А и В ₁ В ₂ В равны по гипотенузе и острому углу. Из их равенства следует равенство катетов: А ₁ А = В ₁ В и АА ₂ = ВВ ₂ или, учитывая координаты точек А ₁ ( х ₁ , у ₁ ), А ₂ ( х ₂ , у ₂ ), В ₁ ( х ₃ , у ₃ ), В ₂ ( х ₄ , у ₄ ), получим х ₂ — х ₁ = х ₄ — х ₃ и у ₂ — у ₁ = у ₄ — у ₃ .т.е. координаты равных векторов равны.

Пусть координаты векторов и равны. Тогда катеты прямоугольных треугольников А ₁ А ₂ А и В ₁ В ₂ В равны и D А ₁ А ₂ А = D В ₁ В ₂ В . Из равенства треугольников следует равенство гипотенуз А ₁ А ₂ и В ₁ В ₂ , т.е. , и параллельность прямых А ₁ А ₂ и В ₁ В ₂ , так как Ð А ₁ А ₂ А = Ð В ₁ В ₂ В . Следовательно, векторы и равны, так как они имеют одинаковые направления и равные длины. Что и требовалось доказать.

Задача 1 . Доказать, что четырехугольник АВС D – параллелограмм, если заданы координаты его вершин: А (2;3), В (4;4), С (8;4), D (6;1). [1]

Решение. Точки А, В, С, D не лежат на одной прямой. Рассмотрим векторы и . Вычислим их координаты , . Координаты векторов одинаковы, поэтому . Из равенства векторов следует, что и , т.е. у четырехугольника ABCD две противолежащие стороны равны и параллельны, следовательно, он – параллелограмм.

Задача 2 . Даны три точки: А (1;1), В (-1;0), С (0;1). Найдите такую точку D ( x ; у ), чтобы векторы и были равны. [4]

Решение. Вектор имеет координаты –2, -1. Вектор имеет координаты х -0, у -1. Так как = , то х -0=-2, у -1=-1. Отсюда находим координаты точки D : х =-2, у =0.

Задача 3. Даны три вершины параллелограмма ABCD : А (1;1), В (3;4), С (8;5). Найти координаты четвертой вершины D и точку пересечения диагоналей. [1]

Решение. Точка пересечения диагоналей – середина каждой из диагоналей. Поэтому она является серединой отрезка АС и имеет координаты:

; .

Так как точка пересечения диагоналей является серединой отрезка BD , можно найти координаты четвертой вершины D :

; .

Видео:Векторы. Метод координат. Вебинар | МатематикаСкачать

§5 Сложение и вычитание векторов

Суммой векторов и с координатами а ₁ , а ₂ и b ₁ , b ₂ называется вектор с координатами а ₁ + b ₁ , a ₂ + b ₂ , т.е.

.

Для любых векторов , , имеют место следующие свойства:

1) (коммутативность);

2) (ассоциативность);

3) .

Для доказательства достаточно срав­нить соответствующие координаты векторов, стоящих в правой и левой частях равенств. Мы видим, что они равны. А векторы с соответственно равными координатами рав­ны.

Теорема. Каковы бы ни были точки А , В , С имеет место векторное равенство .

Доказательство. Пусть , , — данные точки (см. рисунок 5). Вектор имеет координаты , , вектор имеет координаты , . Следовательно, вектор имеет координаты , . А это есть координаты вектора . Значит, векторы и равны. Теорема доказана.

Д

оказанная теорема дает воз­мож­ность следующего графического пос­трое­ния суммы произвольных векторов и . Надо от конца вектора отложить вектор равный вектору . Тогда вектор, начало которого совпадает с началом вектора , а конец – с концом вектора , будет суммой векторов и (см. рисунок 6). Такой способ на­зы­ва­ет­ся «правилом треугольника» сложения векторов.

Для двух векторов с общим началом сумма может также изо­бражаться диагональю параллелограмма, построенного на этих векторах. Такой метод построения на­зывается «пра­ви­лом параллело­грамма». Действительно, , а . Значит, (см. рисунок 7).

Разностью векторов и называется такой вектор , который в сумме с вектором дает вектор : . Отсюда находим координаты вектора : , . Очевидно, что вектор совпадает с диагональю параллелограмма, построенного на векторах и . Началом его является конец вычитаемого вектора , концом – конец уменьшаемого вектора (см. рисунок 7).

Задача 1 . С какой силой F надо удерживать груз весом Р на наклонной плоскости, чтобы он не сползал вниз (см. рисунок 8). [4]

Решение . Пусть О – центр тяжести груза, к которому приложена сила Р . Разложим вектор по двум взаимно перпендикулярным направлениям, как показано на рисунке. Сила перпендикулярна наклонной плоскости и не вызывает перемещения груза. Сила , удерживающая груз, должна быть равной по величине и противоположной по направлению силе . Поэтому .

Задача 2 . Докажите, что точка Х лежит на прямой АВ тогда и только тогда, когда для некоторого t и любой точки O . [5]

Решение. Точка Х лежит на прямой АВ тогда и только тогда, когда , т.е. .

Задача 3. Дано несколько точек и для некоторых пар ( А,В ) этих точек взяты векторы , причем в каждой точке начинается столько же векторов, сколько в ней заканчивается. Докажите, что сумма всех выбранных векторов равна . [5]

Решение. Возьмем произвольную точку О и запишем все выбранные векторы в виде . В силу условия задачи каждый вектор , в сумму всех выбранных векторов войдет со знаком «плюс» столько же раз, сколько и со знаком «минус». Следовательно, сумма этих векторов будет
равна .

Видео:ВЫЧИТАНИЕ ВЕКТОРОВ ЧАСТЬ I #егэ #огэ #математика #геометрия #профильныйегэСкачать

§7 Умножение вектора на число

Произведением вектора на число называется вектор , т.е. .

Операция умножения вектора на число обладает следующими свойствами для любых векторов и любых чисел:

1) , ;

2) (ассоциативность);

3) (дистрибутивность относительно векторного мно­жи­теля;

4) (дистрибутивность относительно числового множи­теля.

Теорема. Абсолютная величина вектора при совпадает с направлением вектора , если , и противоположно направлению вектора , если .

Д
оказательство. Построим векторы и , равные и соответственно (О – начало координат). Пусть и — координаты вектора . Тогда координатами точки А будут числа и , а координатами точки В будут и (см. рисунок 9). Уравнение прямой ОА имеет вид: .

Так как уравнению удовлетворяют координаты точки , то ему удовлетворяют и координаты точки . Отсюда следует, что точка В лежит на прямой ОА . Координаты и любой точки С , лежащей на полупрямой ОА , имеют те же знаки, что и координаты и полупрямой, дополнительной к ОА , имеют противоположные знаки.

Поэтому если , то точка В лежит на полупрямой ОА , а следовательно, векторы и одинаково направлены. Если , то точка В лежит на дополнительной полупрямой, векторы и противоположно направлены.

Абсолютная величина вектора равна:

.

Задача 1 . Даны векторы , . Найти координаты вектора . [1]

Решение . Координаты векторов будут равны и . Разность векторов и имеет координаты, равные разности координат векторов и , т.е. .

Видео:ВЕКТОРЫ решение задач 9 класс АтанасянСкачать

§8 Разложение вектора по двум неколлинеарным векторам

Теорема. Необходимым и достаточным условием коллинеарности векторов и отличных от нуля является существование числа такое, что .

Доказательство. Допустим, векторы и одинаково направлены. Векторы и одинаково направлены и имеют одну и ту же абсолютную величину . Значит, они равны: , .

В случае противоположно направленных векторов и аналогично заключаем, что , , что и требовалось доказать.

Пусть и — отличные от нуля неколлинеарные векторы. Докажем, что любой вектор можно представить в виде .

Пусть А и В – начало и конец вектора (см. рисунок 10). Проведем через точки А и В прямые, параллельные векторам и . Они пересекутся в некоторой точке С . Имеем: . Так как векторы и коллинеарны, то . Так как векторы и коллинеарны, то . Таким образом, , что и требовалось доказать.

Видео:Разбор контрольной работы по геометрии: Векторы в пространствеСкачать

§9 Скалярное произведение векторов

Скалярным произведением векторов и называется число .

Для скалярного произведения векторов используется такая же запись, как и для произведения чисел. Скалярное произведение обозначается и называется скалярным квадратом. Очевидно, .

Скалярное произведение обладает следующими свойствами:

1) (коммутативность);

2) (ассоциативность);

3) (дистрибутивность).

Углом между ненулевыми векторами и называется угол ВАС . Угол между любыми двумя ненулевыми векторами и называется угол между равными им векторами с общим началом. Угол между одинаково направленными векторами считается равным нулю.

Теорема. Скалярное произведение векторов равно произведению их абсолютных величин на косинус угла между ними.

Доказательство. Пусть и – данные векторы и – угол между ними. Имеем:

,

.

Отсюда видно, что скалярное произведение выражается через длины векторов , и , а поэтому не зависит от выбора системы координат, т.е. скалярное произведение не изменится, если систему координат выбрать специальным образом. Возьмем систему координат ху так, как показано на рисунке 11. При таком выборе системы координат координатами вектора будут и 0 , а координатами вектора будут и . Скалярное произведение . Теорема доказана.

Из доказанной нами теоремы следует, что если векторы перпендикулярны, то их скалярное произведение равно нулю. И обратно: если скалярное произведение отличных от нуля векторов равно нулю, то векторы перпендикулярны.

Задача 1 . Даны векторы и . Найти длину вектора , если известно, что =4, =3, а угол между векторами и равен 60 ° . [1]

Решение. Согласно одного из свойств скалярного произведения векторов , . Следо­ва­тельно, .

Задача 2 . Вычислить косинусы углов А и В треугольника АВС , вершины которого имеют следующие координаты: А (1;6), В (1;1), С (4;1). [1]

Решение. Согласно определению скалярного произведения векторов и , , найдем .

Вычислим координаты векторов и : , , ; .

Затем вычислим координаты векторов и : (0;5), (3;0), . Следовательно, ^ , и .

Задача 3 . В точках М ₁ ( х ₁ ; у ₁ ), М ₂ ( х ₂ ; у ₂ ) сосредоточены массы, соответ­ственно равные m ₁ и m ₂ . Найти координаты центра тяжести системы этих
масс. [1]

Решение. Известно, что центр масс С лежит на отрезке М ₁ М ₂ и удален от точек М ₁ и М ₂ на расстояние, обратно пропорциональные массам m ₁ и m ₂ , т.е. точка С , являющаяся центром тяжести системы двух материальных точек, делит отрезок М ₁ М ₂ в отношении . Используя формулы для нахождения координат середины отрезка ; и подставляя в них значение , после преобразований находим координаты точки С:

; .

Задача 4. Пусть О – центр описанной окружности треугольника АВС , а точка Н обладает тем свойством, что . Докажите, что Н – точка пересечения высот треугольника АВС . [5]

Решение. Докажем что .

и , поэтому , так как О – центр описанной окруж­нос­ти. Аналогично доказывается, что и .

Видео:9 класс, 1 урок, Разложение вектора по двум неколлинеарным векторамСкачать

§10 Разложение вектора по координатным осям

Вектор называется единичным, если его абсолютная величина равна единице. Единичные векторы, имеющие направления положительных координатных полуосей, называются коор­ди­нат­ными векторами или ортами. Обычно их обоз­начают следующим образом на оси х и на оси у (см. рисунок 12).

Так как координатные векторы отличны от нуля и не коллинеарны, то любой вектор допускает разложение по этим векторам:

. (*)

Найдем коэффициенты и этого разложения. Умножим обе части равенства (*) на вектор . Так как

, , , то .

Аналогично, умножая обе части равенства (*) на вектор получим .

Таким образом, для любого вектора получается разложение

.

Задача 1. Найти координаты единичного вектора, одинаково нап­равленного с вектором (3;4).

Решение. Длина вектора равна . Длина единичного вектора , направленного одинаково с вектором , равна единице.

Чтобы вычислить координаты вектора , разделим обе части предыдущего равенства на :

.

Следовательно, координаты единичного вектора , одинаково направленного с вектором , равны .

Видео:Скалярное произведение векторов. 9 класс.Скачать

Набор упражнений для самостоятельного решения
учащимися

1. Даны вектор и точка С . Отложите от точки С вектор, равный вектору , если: 1) точка С лежит на прямой ; 2) точка С не лежит на прямой .

2. Векторы , , отложены от начала координат. Чему равны координаты их концов?

3. Даны векторы: (-3;-1), (4;0), (5;-2). Найти координаты векторов:
а) 2 ; б) — +3 ; в) 2 +3 -5 ; г) .

4. Воспользовавшись условием коллинеарности двух векторов, выяснить, коллинеарны ли векторы:

а) и , б) и .

5. Докажите, что для векторов , и имеет место неравенство .

6. К горизонтальной балке на двух равных нитях подвешен груз весом Р . Определите силы натяжения нитей (рисунок 13).

7. В треугольнике ABC проведена медиана АМ . Докажите, что .

8. Найдите угол между векторами и .

9. Даны четыре точки А (0;0), В (1;1), С (0;2), D (-1;1). Докажите, что четырехугольник АВС D – квадрат.

10. Даны вершины треугольника А (1;1), В (4;1), С (4;5). Найдите косинусы углов треугольника.

11. Доказать, что точка М пересечения медиан треугольника с вершинами в точках , , имеет координаты:

; .

12. Докажите, что геометрическое место точек, сумма квадратов расстояний от которых о двух данных точек постоянна, есть окружность с центром в середине отрезка, соединяющего данные точки.

13. Докажите, что проекция вектора на ось абсцисс с координатным вектором задается формулой , где .

Видео:Как выражать вектор? Как решать задачу с вектором? | TutorOnlineСкачать

Список использованных источников

1. Герасимович А.И., Пушкина-Варварчук Г.Т., Шарикова З.П., Цыганова В.К. Геометрия для подготовительных отделений втузов: Справ. Пособие – Мн.: Выш. Шк., 1987.

2. Колягин Ю.М., Оганесян В.А. и др. Методика преподавания математики в средней школе. Общая методика – учеб. пособие для студентов физ.-мат. факт. пед. институтов. М.: Просвящение, 1975.

3. Колягин Ю.М., Оганесян В.А. и др. Методика преподавания математики в средней школе. Частные методики – учеб. пособие для студентов физ.-мат. факт. пед. институтов. М.: Просвящение, 1977.

4. Погорелов А.В. Геометрия: Учеб. для 7-11 кл. сред. шк. – 3-е
изд. – М.: Просвещение, 1992.

5. Прасолов В.В. Задачи по планиметрии. — 4-е изд., дополнен-
ное — М.: Изд-во Московского центра непрерывного математического образования, 2001 (эл. версия).

6. Программы средней общеобразовательной школы. Математи-
ка – М.: Просвещение, 1988.

7. Рогановский Н.М. Методика преподавания математики в ср. шк.: Учебное пособие – Выш. шк., 1990.

8. Цыпкин А.Г., Пинский А.И. Справочное пособие по методам решения задач по математике для средней школы. /Под. ред. Блогодатс-
ких В.И. – М.: Наука. Главная редакция физико-математической литературы, 1983.

📹 Видео

Понятие вектора. Коллинеарные вектора. 9 класс.Скачать