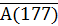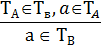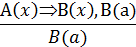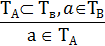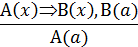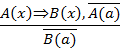Круги эйлера четырехугольник квадрат ромб (7 видео)

Тема 4. Математические доказательства

Методические рекомендации

Задания под номером 10 в контрольной работе, предлагаемые по данной теме, связаны с оценкой правильности сделанного умозаключения, либо с его построением.

При анализе умозаключения выделяют его логическую структуру, а затем проверяют соответствие полученной схемы одному из известных правил вывода. Если такое соответствие имеет место, то рассуждение правильно, если же нет, то надо провести дальнейший анализ умозаключения. Для этого выделенную схему записывают на теоретико-множественном языке и с помощью кругов Эйлера изображают посылки, считая их истинными. Затем выясняют, всегда ли при этом истинно заключение. Если возможна ситуация, при которой заключение оказывается ложным, то умозаключение неправильно.

При решении задач другого типа требуется самостоятельно построить правильное умозаключение. В этих случаях надо ориентироваться на какую-либо из известных схем правильных умозаключений.

Образец выполнения заданий

Задание 10. Правильные и неправильные умозаключения

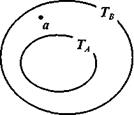
Задача. Правильно ли умозаключение: «Все студенты нашей группы закончили педучилище. Студентка b не закончила педучилище. Следовательно, она не учится в нашей группе».

1 способ. Выделим логическую структуру умозаключения, для этого обозначим через А(х) предложение «х – студентка нашей группы», через В(х) – предложение «х – закончила педучилище». Тогда первая посылка имеет вид: А(х) В(х).

Вторая посылка: .

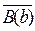
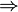
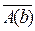
Заключение: , где b – данная студентка.

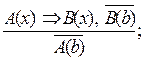Круги эйлера четырехугольник квадрат ромб

является правилом отрицания. Следовательно, рассуждение правильно.

2 способ. Данное умозаключение запишем на теоретико-множественном языке.

Первая посылка. В ней утверждается, что множество (А) студентов группы является подмножеством множества (В) студентов, окончивших педучилище, т.е. что А Ì В.

Вторая посылка. Утверждается, что студентка b не заканчивала педучилище, т.е. что b ∉ В.

Заключение. Утверждается, что она не является студенткой группы, т.е. b ∉ А.

Схема умозаключения на теоретико-множественном языке имеет вид:

Изобразим посылки с помощью кругов Эйлера (рис. 5). Видим, что если А Ì В и b ∉ В, то при этом обязательно b ∉ А.

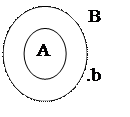Данная схема такова, что истинность посылок гарантирует истинность заключения. Значит, рассуждение правильное.

Варианты контрольной работы

Вариант 1

1. Приведите примеры двух заданий из учебников математики для начальных классов, при выполнении которых осуществляется переход от одного способа задания множества к другому. Выбор обоснуйте.

2.Известно, что К – множество мальчиков класса, L – множество учащихся класса, занимающихся в кружке по рисованию. Сформулируйте условия, при которых: а) К∩L=Ø; б) К∩L=К.

3. Найти множество D = (A’∩ B) С, если А = (- ∞; 2), В = (0; 5], С = [3; 7)

4. Изобразите на координатной плоскости элементы множества X×Y, если:

2.Известно, что А – множество спортсменов класса, В – множество отличников класса. Сформулируйте условия, при которых: а) В∩А≠Ø;

3.Найти множество P = A È (B’_R C), если А = [0; 3), В = (-∞; 2) 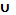[5; +∞),

4. Изобразите на координатной плоскости элементы множества X×Y, если:

9. Сформулируйте признак делимости на 3, используя слова «тогда и только тогда, когда», «необходимо и достаточно». Сформулируйте теоремы, выражающие необходимый, достаточный признак делимости на 3.

10. Закончите умозаключение, используя правило отрицания: «Во всяком прямоугольнике сумма внутренних углов равна 360 . В четырехугольнике ABCD …». Ответ обоснуйте.

Вариант 10

2. Проиллюстрируйте с помощью кругов Эйлера высказывания:

а) Все мальчики 5 «А» класса участвовали в туристическом походе.

б) Ни один мальчик 5 «А» класса не является неуспевающим учеником.

3.Найти множество D = (A 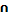B’_R) C, если А = [-4; 6), В = [3; 7), С = [2; 5].

4.Изобразите на координатной плоскости элементы множества X×Y, если:

Содержание

Презентация по математике «Круги Эйлера»
«Управление общеобразовательной организацией: новые тенденции и современные технологии»
Схемы дедуктивных умозаключений. Рассмотрим подробнее дедуктивные (правильные) умозаключения
💡 Видео

Видео:Геометрия 8. Урок 4 - Прямоугольник, ромб, квадрат - свойства и признаки.Скачать

Презентация по математике «Круги Эйлера»

Видео:Параллелограмм, прямоугольник, ромб,квадрат,трапеция, все свойства и определения!!!Скачать

«Управление общеобразовательной организацией:
новые тенденции и современные технологии»

Свидетельство и скидка на обучение каждому участнику

Описание презентации по отдельным слайдам:

Цели: -изучить теорию множеств и подмножеств; — научиться составлять и решать задачи с помощью кругов Эйлера; Задачи: — Собрать материал по данной теме; — Глубже изучить дополнительную литературу и историю развития математики. Методы: — беседы, — опрос учащихся.

Множества и подмножества В математике некоторые понятия являются неопределяемыми. Одним из таких неопределяемых понятий является понятие «подмножества». Во многих вопросах приходится рассматривать некоторую совокупность элементов как единое целое. Так, биолог, изучая животный и растительный мир данной области, классифицирует все особи по видам, виды родам и т. д. Каждый вид является некоторой совокупностью живых существ, рассматриваемой как единое целое. Для математического описания таких совокупностей и было введено понятие множества. По словам одного из создателей теории множеств – немецкого математика Георга Кантора (1845 – 1918) «Множество есть многое, мыслимые нами как единое» Из этих слов ясно, что можно говорить о множестве натуральных чисел, множестве треугольников и т.д.

Множества, состоящие из конечного числа элементов, называются конечными, а остальные множества – бесконечными. НАПРИМЕР, множество китов в океане конечно, а множество рациональных чисел бесконечно. Конечные множества могут быть заданы перечислением их элементов (например, множество учеников в данном классе задается их списком в журнале); если множество А состоит из элементов а, в, с, то пишут А= Бесконечные множества нельзя задать перечнем их элементов. Их задают указывая свойство, которым обладают все элементы данного множества, но не обладают никакие элементы, не принадлежащие этому множеству. Множества, состоящие из одних и тех же элементов, называют равными (совпадающими). НАПРИМЕР,, равны множество равносторонних треугольников и множество равноугольных треугольников, т.к. это одни и те же треугольники. Если в треугольники все стороны равны, то равны и все углы. Любой квадрат является прямоугольником. Говорят, что множество квадратов является частью множества прямоугольников, или на языке математики является подмножеством. Если множество А является подмножеством множества В, то пишут А В. например, множество натуральных чисел является подмножеством целых чисел N Z U U

. Операции над множествами. Над множествами можно производить различные операции. Простейшие из них: — объединение — пересечение, — дополнение. Объединением двух множеств называется множество, состоящее из всех элементов, принадлежащих хотя бы одному из этих множеств. Объединение множеств А и В обозначается А U В. На рисунке объединение двух множеств выделено двойной штриховкой. Пример: множество многоугольников является объединением множества треугольников, четырехугольников, пятиугольников… п – угольников. А В

Пересечением двух множеств называется множество, состоящее из всех элементов, принадлежащих одновременно обоим множествам. Пересечением множества А и В обозначается А∩В. На рисунке пересечение двух множеств выделено двойной штриховкой. Пример: пересечением множества ромбов со множеством прямоугольников является множество квадратов. А В

Дополнением множества В до множества А называется множество всех элементов из А, не принадлежащих В. Дополнение множества В до множеств А обозначается АВ. На рисунке дополнение выделено зеленым цветом. Пример: А – множество всех натуральных чисел, кратных 2: А В –множество натуральных чисел, кратных 6, т.е. кратных и 2 и 3: В Дополнением В до множества А является множество всех натуральных чисел, кратных 2, т.е. . В В А

Круги Эйлера. Задача №1. Мною были опрошены учащиеся 5-9 классов нашей школы. Я выбрала 3 кружка: Танцевальный (Т) Волейбол (В) «Драматический» (Д). В 5-9 классах учатся 45 учащихся. Из них занимаются в Т – 20 учащихся, в В – 22 учащихся, в Д – 14 учащихся. 10 учащихся не посещают ни один из этих кружков. Посещают 2 кружка: Т и В — 8 учащихся, Т и Д – 4 учащихся, В и Д – 3 учащихся. а) Сколько учащихся одновременно посещают все 3 кружка? б) Сколько учащихся посещают 1 из этих кружков?

Решение: Воспользуемся кругами Эйлера. Множество всех учащихся изобразим большим кругом. Внутри этого круга тремя маленькими кругами покажем множества элементов (учащихся) Т, В, Д. Число учащихся всех трех множеств равно Х. Из рассмотрения кругов Эйлера видно, что число элементов множеств Т, В, равно 14 – 4 – 3 – Х = 7 – Х, число элементов множеств Т и Д равно 22 – 8 – 3 – Х = 11 – Х, число элементов множеств В и Д равно 20 – 4 – 8 – Х = 8 – Х. Пользуясь тем, что множество разбилось на непересекающиеся подмножества, составляем уравнение: (7 – Х) + (11 – Х) + (8 – Х) + 10 + 8 + 3 + 4 = 45. 7 – Х + 11 – Х + 8 – Х + 25 = 45. — 3Х = 45 – 51. — 3Х = — 6 Х=2. Таким образом, 2 учащихся посещают все 3 кружка. Найдем элементы непересекающихся множеств: 7 – 2 = 5; 11 – 2 = 9; 8 – 2 = 6. Складываем полученные количества элементов непересекающихся множеств: 5 + 9 + 6 = 20 Таким образом, 20 учащихся посещают лишь 1 из этих кружков. 10 Т-20 Д-14 В-22 4 3 8 х

Задача № 2. Из числа учащихся 7 -9 классов были опрошены 24 ученика. Был поставлен вопрос: чему отдают предпочтение: чтению книг (КН), общению с компьютером (К) или просмотру телепередач (ТП)? Большее количество учащихся отдали предпочтение просмотру телепередач и общению с компьютером – 17, из них 2 любят читать книги. Тот, кто отлично разбирается в компьютерных играх, не любят читать книги и смотреть телепередачи. А два его друга, которые любят телепередачи, на компьютере не играют, зато книголюбы. Среди любителей книг есть 4, которые не играют в компьютер и не любят телепередачи. а) Сколько учащихся любят читать книги? б) Сколько учащихся любят играть на компьютере? в) Сколько учащихся любят смотреть телепередачи? РЕШЕНИЕ: Изобразим задачу при помощи кругов Эйлера. Число учащихся равно 15 + 2 + 2 + 1 + 4 = 24. Теперь нетрудно ответить на вопросы: — любят читать книги – 8, — играть на компьютере – 18, — смотреть телепередачи – 19. Таким образом, из этой задачи видно, что проблема читаемости является проблемой учащихся и нашей школы. Книги — 4 Телепередачи Компьютер -1 2 2 0 15

Задача №3. Из числа учащихся 5-7 классов одни владеют родным (бурятским) языком, другие не владеют. Мальчиков – 13. Владеющих бурятским языком, мальчиков и девочек – 23, не владеющих бурятским языком девочек столько, сколько мальчиков, владеющих бурятским языком. Сколько всего учащихся было опрошено? Решение: Снова воспользуемся кругами Эйлера. Множество мальчиков обозначим буквой М, множество девочек – Д, множество владеющих бурятским языком – В, множество не владеющих бурятским языком – Н. Из условия видно, что множества ВМ и НМ вместе содержат 13 элементов, а множества ВМ и ВД содержат 23 элемента, множество ВМ содержит столько же элементов, сколько и множество НД. Значит множества ВД и НД (девочек) содержат также 23 элемента, т. е. девочек 23. Значит, опрошено всего 23 + 13 =36 учащихся. М Д В Н ВМ ВД НМ НД

Задача №4 В 5-7 классах 36 учеников. Из них 21 ученик имеют «3» по русскому языку (Р), 17 учащихся – по математике (М), 10 учащихся не имеют «3» по этим предметам. Сколько учащихся имеют «3» и по математике и по русскому языку (МР)? Решение: Изобразим круги Всех детей 36, из них 10 не имеют «3», значит внутри двух меньших кругов находится 36 – 10= 26, т.е. они имеют «3». Внутри круга М находится 17 детей, значит в той части круга Р, которая расположена вне круга М, находится 26 – 17 = 9 детей. Остальные 21 – 9 = 12 уч-ся находятся в общей части круга МР. Значит, 12 учащихся имеют «3» и по русскому языку и по математике. 10 М — 17 Р – 21 36-10-17=9 21-9=12 МП

Заключение Таким образом, работая над этой темой я расширила свой математический кругозор. Я узнала много нового и интересного о Леонарде Эйлере. В ходе изучения этой темы я научилась правильно рассуждать, сравнивать и овладела новым методом решения задач – круги Эйлера. Был проведен опрос среди учащихся 5–9 классов, по результатам которого я составила задачи, в одной из которых была затронута проблема читаемости. В последнее время проблеме читаемости стали уделять больше внимания. В октябре месяце прошел конкурс «Самый читающий класс», «Самый читающий школьник», где я принимала активное участие, «Самая читающая семья» и т.д. Именно такие мероприятия повышают интерес к чтению книг, в том числе на родном языке. Участие в этом мероприятии толкнуло меня на мысль провести исследовательскую работу в своей школе, вывод которой я показала с помощью кругов Эйлера: низка читаемость учащихся, не все дети современные владеют родным языком. Однако круги Эйлера позволяют сделать выводы и по другим вопросам, например уровень успеваемости и успешности учеников 5 – 9 классов. Я думаю, что моя работа является актуальной и значимой по многим вопросам не только школьной жизни.

Видео:Как решить любую задачу с четырёхугольниками? | Математика TutorOnlineСкачать

Схемы дедуктивных умозаключений. Рассмотрим подробнее дедуктивные (правильные) умозаключения

Рассмотрим подробнее дедуктивные (правильные) умозаключения. Согласно определению (п. 25), в дедуктивном умозаключении посылки и заключение находятся в отношении логического следования. Это означает, что в нем всегда из истинных посылок следует истинное заключение. Но как строить такие умозаключения и проверять их правильность?

В логике считают, что правильность умозаключения определяется его формой и не зависит от конкретного содержания входящих в него утверждений. И в логике предлагаются такие правила, соблюдая которые, можно строить дедуктивные умозаключения. Эти правила называют правилами вывода или схемами дедуктивных (правильных) умозаключений. Правил много, но наиболее часто используются следующие:

-правило заключения;

— правило отрицания;

—правило силлогизма.

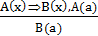
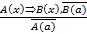
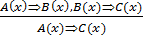
Выясним, что обозначают все знаки, использованные в записи этих правил; как их применять на практике.

Рассмотрим, например, правило заключения. В нем обозначены две посылки А(х) => В(х) и А (а). Первую называют общей посылкой, это может быть теорема, определение и, вообще, предложение вида А(х) => В(х). Вторую посылку А(а) называют частной, она получается из условия А(х) при х = а. Предложение В(а) — это заключение, оно получается из В(х) при х = а. Посылки отделены от заключения чертой, которая заменяет слово «следовательно».

Приведем пример умозаключения, выполненного по правилу заключения:

Если запись числа х оканчивается цифрой 5, то число х делится на 5. Запись числа 135 оканчивается цифрой 5. Следовательно, число 135 делится на 5.

В качестве общей посылки в этом умозаключении выступает утверждение вида «если А(х), то В(х)», где А(х) — это «запись числа x оканчивается цифрой 5», а В(х) — «число х делится на 5». Частная посылка представляет собой высказывание, которое получилось из условия общей посылки при х = 135 (т.е. это Л(135)). Заключение является высказыванием, полученным из В(х) при х = 135 (т.е. это 5(135)).

Приведем теперь пример умозаключения, выполненного по правилу отрицания: Если запись числа х оканчивается цифрой 5, то число х делится на 5. Число 177 не делится на 5. Следовательно, оно не оканчивается цифрой 5.

Видим, что в этом умозаключении общая посылка такая же, как и в предыдущем, а частная представляет собой отрицание высказывания «число 177 делится на 5» (т.е. это 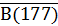). Заключение — это отрицание предложения «Запись числа 177 не оканчивается цифрой 5» (т.е.

И наконец, рассмотрим пример умозаключения, построенного по правилу силлогизма.

Если число х кратно 12, то оно кратно 6. Если число х кратно 6, то оно кратно 3. Следовательно, если число х кратно 12, то оно кратно 3.

В этом умозаключении две посылки вида «если А(х), то В(х)» и «если В(х), то С(х)», где А(х) — это предложение «х кратно 12», В(х) -предложение «х кратно 6» и С(х) — предложение «х кратно 3». Заключение представляет собой высказывание «если А (х), то С(х)».

Конечно, возникает вопрос, почему умозаключения, выполненные по правилам заключения, отрицания и силлогизма, будут дедуктивными (правильными)? Дело в том, что, выполняя рассуждения по этим правилам, мы всегда будем получать истинное заключение, что и требуется в дедуктивном умозаключении. Убедиться в этом можно, если воспользоваться кругами Эйлера.

В логике существуют различные способы проверки правильности умозаключений. Мы рассмотрим тот, который предполагает использование кругов Эйлера. Сначала данное умозаключение можно записать на теоретико-множественном языке, затем посылки изобразить на кругах Эйлера, считая их истинными. После этого надо выяснить, всегда ли при таких посылках истинно заключение. Если оказывается, что всегда, то говорят, что данное умозаключение правильное, дедуктивное. Если же возможен рисунок, из которого видно, что заключение может быть ложным, то говорят, что всякое умозаключение, выполненное по такой схеме, является недуктивным, неправильным.

Покажем, что умозаключение, выполненное по правилу заключения, является дедуктивным. Сначала запишем это правило на теоретико-множественном языке.

Посылка А (х) => В(х) может быть записана в виде Т_А Ì Т_В, где Т_А и Т_в — множества истинности высказывательных форм А (х) и В(х).

Частная посылка А(а) означает, что а Î Т_А, а заключение В(а) показывает, что а Î Т_В.

Все умозаключение, построенное по правилу заключения, запишется на теоретико-множественном языке так:

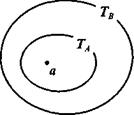Рис. 37

Изобразив на кругах Эйлера множества Т_А и Т_B, и обозначив элемент а Î Т_А, мы увидим, что а Î Т_B (рис. 37), т. е. а Î Т_АÞа Î Т_B. Аналогичным образом можно проверить и другие правила дедуктивных умозаключений. Кроме того, такой способ проверки правильности умозаключений можно использовать и в тех случаях, когда умозаключение выполнено по схеме, отличной от рассмотренных.

Задача. Правильно ли следующее умозаключение: «если запись числа оканчивается цифрой 5, то число делится на 5. Число 125 делится на 5. Следовательно, запись числа 125 оканчивается цифрой 5».

Решение. Это умозаключение выполнено по схеме

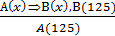
которую в общем виде можно представить так:

Но такой схемы среди названных выше нет. Является ли она правилом дедуктивного умозаключения?

Чтобы ответить на этот вопрос, воспользуемся кругами Эйлера. На теоретико-множественном языке полученное правило можно записать так:

Изобразим на кругах Эйлера множества Т_А и Т_В и обозначим элемент а, принадлежащий множеству Т_В. Но оказывается, что он может содержаться в множестве Т_А, а может и не принадлежать ему (рис. 38).

Рис. 38

В логике считают, что такая схема не является правилом дедуктивного умозаключения, так как она не гарантирует истинности заключения. И вообще при анализе умозаключения нельзя отождествлять правильность умозаключения с истинностью полученного заключения: заключение может быть истинным, а само умозаключение не быть дедуктивным, правильным.

Возвращаясь к вопросу нашей задачи, скажем, что данное в ней умозаключение не является правильным, так как выполнено по схеме, не гарантирующей истинности заключения.

Как же надо действовать, чтобы установить, правильно ли умозаключение или нет? Для этого есть два пути. Первый — это показать данное умозаключение выполнено по одному из известных правил вывода. Второй — сформулировать данное умозаключение на теоретико-множественном языке и воспользоваться кругами Эйлера так, как описано выше.

Полезно запомнить и не путать с правилом заключения такую схему:

а с правилом отрицания схему:

Эти схемы не гарантируют истинности заключения и, следовательно, не являются правилами дедуктивных умозаключений.

Заметим, что полное дедуктивное умозаключение по приведенным трем правилам требует указания двух посылок. Однако в процессе рассуждений эти правила иногда сокращают, опуская одну из посылок. Например, объясняя, почему 6

Не нашли, что искали? Воспользуйтесь поиском: