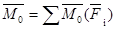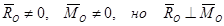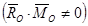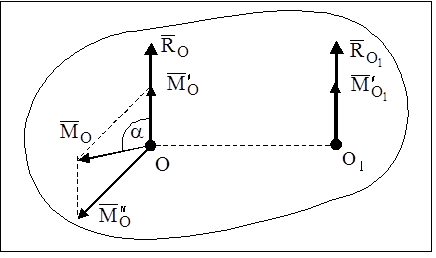Теорему пуансо главный вектор и главный момент плоской системы сил (8 видео)

Приведение системы сил к заданному центру.

Лекция 3

Краткое содержание: Приведение произвольной и плоской системы сил к центру. Теорема о параллельном переносе силы, основная теорема статики Приведении системы сил к данному центру Главный вектор и главный момент системы сил. Зависимость главного момента от выбора центра. Аналитическое определение главного вектора и главного момента системы сил. Инварианты системы сил. Приведение системы сил к простейшему виду. Частные случаи приведения произвольной системы сил, динамический винт. Теорема Вариньона о моменте равнодействующей.

Приведение силы к заданному центру (Лемма Пуансо)

Равнодействующая системы сходящихся сил непосредственно находится с помощью сложения сил по правилу параллелограмма. Очевидно, что аналогичную задачу можно будет решить и для произвольной системы сил, если найти для них метод, позволяющий перенести все силы в одну точку.

Лемма Пуансо о параллельном переносе силы.. Не изменяя действия силы на твердое тело, ее можно переносить параллельно самой себе в любую точку тела, добавляя при этом пару, момент которой равен моменту данной силы относительно новой точки приложения.

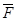
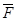
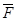
Пусть сила приложена в точке A. Действие этой силы не изменяется, если в точке B приложить две уравновешенные силы. Полученная система трех сил представляет собой силу равную , но приложенную в точке В и пару с моментом . Процесс замены силы силой и парой сил называется приведением силы к заданному центру В . ■

Приведение системы сил к заданному центру.

Главным вектором системы сил называется вектор, равный векторной сумме этих сил.

Главным моментом системы сил относительно точки О тела, называется вектор, равный векторной сумме моментов всех сил системы относительно этой точки.

Теорема Пуансо (Основная теорема статики)

Произвольную систему сил, действующую на твердое тело, можно заменить эквивалентной системой, состоящей из силы и пары сил. Сила равна главному вектору системы сил и приложена в произвольно выбранной точке (центре приведения), момент пары равен главному

моменту системы сил относительно этой точки.

Точка О — центр приведения. По лемме Пуансо перенесем силу F1 в точку О. При этом вместо F1 имеем в точке О такую же силу F1’ и дополнительно пару сил с моментом m1.

Аналогично перенесем все остальные силы. В результате получим систему сходящихся сил и систему пар сил. По теореме о существовании равнодействующей системы сходящихся

сил их можно заменить одной силой R, равной главному вектору. Систему пар по теореме о сложении пар можно заменить одной парой, момент которой равен главному моменту Mo. ■

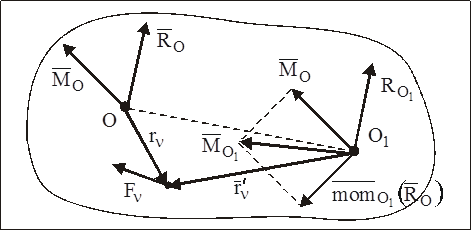
Инварианты статики — характеристики системы сил, не зависящие от выбора центра приведения.

Первый инвариантстатики — главный вектор системы сил (по определению).

Второй инвариантстатики — скалярное произведение главного вектора и главного момента.

В самом деле, главный момент, очевидно, зависит от выбора центра приведения. Рассмотрим произвольную систему сил . Приведем ее сначала к центру О, а затем к центру О₁ .

Из рисунка видно ,что .Поэтому формула для примет вид

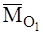
Или .

Домножим обе части этого равенства на соответственно, учитывая что главный вектор системы сил является первым инвариантом статики: . По

свойству смешанного произведения векторов , следовательно:

Если воспользоваться определением скалярного произведения, то для второго инварианта можно получить еще одну форму:

Так как , то предыдущее выражение примет вид:

Таким образом, проекция главного момента на направление главного вектора есть величина постоянная для данной системы сил и не зависит от выбора центра приведения.

Частные случаи приведения произвольной системы сил к простейшему виду

1) Если при приведении системы сил к центру О то на основании (6.4) можно записать

В этом случае система сил приводится к равнодействующей, приложенной в центре приведения и совпадающей по величине и направлению с главным вектором.

2)Если при приведении системы сил к центру О

то представив в виде пары сил с плечом ,

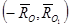
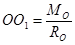
получим: .

В этом случае система сил приводится к равнодействующей, совпадающей по величине и направлению с главным вектором, а линия действия равнодействующей отстоит от линии действия главного вектора на расстоянии .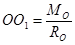

3)Если при приведении системы сил к центру О то можно записать

,то есть система сил приводится к паре сил с моментом, равным главному моменту системы сил.

4)Если при приведении системы сил к центру О то можно записать

, т.е. система сил находится в равновесии.

Определение: Система, состоящая из силы и пары сил, момент которой коллинеарен силе (плоскость пары перпендикулярна линии действия силы), называется динамой или динамическим винтом.

Если при приведении системы сил к центру О второй инвариант не равен нулю, то эта система сил приводится к динаме.

Разложив на две составляющие — вдоль главного вектора и — перпендикулярно главному вектору, для и будем иметь случай 2),а вектор , как свободный можно перенести параллельно самому себе в точку О₁:

Вектора представляют собой динаму, где , .

В рассматриваемом случае приведения системы сил главный момент имеет минимальное значение. Это значение момента сохраняется при приведении заданной системы сил к любой точке, лежащей на линии действия главного вектора и главного момента . Уравнение этой линии( центральная винтовая ось системы сил) определяется из условия коллинеарности векторов и : .

С учетом , ,

уравнение центральной оси в векторной форме можно записать так:

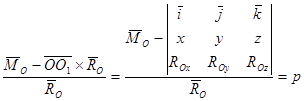
Проектируя это соотношение на оси декартовой системы координат с началом в центре приведения О, получим:

Здесь x, y, z – координаты точек, лежащих на центральной оси, а р – постоянная линейная величина, называемая параметром динамы.

Теорема Вариньона.

Если система сил имеет равнодействующую, то ее момент относительно любого центра равен сумме моментов всех сил системы относительно того же центра.

Пусть , а — точка на линии действия равнодействующей. Как было доказано: ,

но = 0, следовательно, ■

Содержание

ПЛОСКАЯ СИСТЕМА ПРОИЗВОЛЬНО РАСПОЛОЖЕННЫХ СИЛ
ПРИВЕДЕНИЕ СИЛЫ К ТОЧКЕ (ТЕОРЕМА ПУАНСО)
ПРИВЕДЕНИЕ ПЛОСКОЙ СИСТЕМЫ СИЛ К ОДНОМУ ЦЕНТРУ. ГЛАВНЫЙ ВЕКТОР И ГЛАВНЫЙ МОМЕНТ
5 Плоская система произвольно расположенных сил 5.1 Теорема Пуансо о параллельном переносе сил
📺 Видео

Видео:2.2. Главный вектор и главный момент плоской системы сил. Приведение к простейшему видуСкачать

ПЛОСКАЯ СИСТЕМА ПРОИЗВОЛЬНО РАСПОЛОЖЕННЫХ СИЛ

Видео:§4.3. Главный вектор и главный момент сил инерцииСкачать

ПРИВЕДЕНИЕ СИЛЫ К ТОЧКЕ (ТЕОРЕМА ПУАНСО)

Плоская система произвольно расположенных сил — это система сил, линии действия которых расположены в одной плоскости произвольным образом.

Рассмотрим случай переноса силы в произвольную точку, не лежащую на линии действия силы.

Теорема. Действие силы на тело не изменится, если ее перенести параллельно самой себе в любую точку тела, присоединяя при этом некоторую пару сил.

Доказательство. Пусть к телу в некоторой точке К приложена сила F (рис. 1.4.1). Перенесем в произвольную точку О того же тела силу F = F’ параллельно данной силе. Но чтобы равновесие не изменилось, к точке О надо приложить равную по величиной противоположно направленную_силу F» (см. рис. 1.4.1).

Силы F’ и F» взаимно уравновешиваются, и поэтому действие на тело одной данной силы F эквивалентно действию на него системы трех сил F, F‘ и F». При этом сила F‘ может рассматриваться как сила F, перенесенная параллельно своему начальному направлению в точку О, а силы F» и F образуют пару, которую мы должны присоединить при параллельном переносе силы из точки К в точку О, чтобы сохранить действие силы при этом переносе. Теорема доказана.

Пару (F» F), образующуюся при переносе точки приложения силы F, называют присоединенной парой.

Видео:Приведение системы сил к простейшему видуСкачать

ПРИВЕДЕНИЕ ПЛОСКОЙ СИСТЕМЫ СИЛ К ОДНОМУ ЦЕНТРУ. ГЛАВНЫЙ ВЕКТОР И ГЛАВНЫЙ МОМЕНТ

Рассмотрим систему нескольких сил F_р F₂, . F , расположенных как угодно на плоскости. Возьмем в плоскости действия сил произвольную точку О (рис. 1.4.2, а), назовем ее центром приведения. Перенесем все_ данные силы в эту точку. Мы получим систему сил F[, F’₂, . F’_n, приложенных в этой точке, и систему пар сил (Fy, F»), (F₂, F₂), . (F_n, F»). Приложенные в точке О силы F, F₂. F’_n можно сложить по правилу многоугольника и, следовательно, заменить одной эквивалентной им равнодействующей силой F у равной их геометрической сумме. Так как силы Fj, F₂,. F’_n геометрически равны данным силам F_р F_v . F_n, то

Вектор F у равный геометрической сумме всех сил данной системы, является главным вектором этой системы (рис. 1.4.2, б),

Модуль и направление главного вектора можно найти по формуле равнодействующей системы сходящихся сил:

Все присоединенные пары (F_v F»), (F₂, F₂), . (F_n, F») можно сложить по правилу сложения пар сил, лежащих в одной плоскости, и, следовательно, заменить их одной результирующей парой. Моменты этих пар равны моментам данных сил F_р F₂, . F_п относительно центра приведения О, т.е.

Отсюда найдем момент результирующей пары М_п:

Алгебраическая сумма моментов относительно какой-то точки О всех данных сил, расположенных произвольным образом на плоскости, называется главным моментом данной плоской системы относительно этой точки (см. рис. 1.4.2, б):

Произвольная точка тела, в которую переносятся параллельно все силы системы, называется точкой (или центром) приведения. Итак, полученный результат можно сформулировать следующим образом: всякую плоскую систему сил всегда можно заменить одной силой, равной главному вектору системы, приложенной в произвольной точке О, и парой, момент которой равен главному моменту данной системы сил относительно этой точки.

Главный вектор системы не является равнодействующей силой для данной системы сил, так как он заменяет данную систему сил вместе с присоединенной парой. Модуль и направление главного вектора не зависят от выбора точки приведения, так как все силы переносятся параллельно их начальному направлению и силовой многоугольник во всех случаях будет одним и тем же.

Величина и знак главного момента зависят от центра приведения, так как с изменением центра приведения изменяются моменты сил относительно этого центра, а следовательно, и их алгебраическая сумма. Поэтому, задавая главный момент, нужно указывать, относительно какой точки он вычислен.

Видео:§ 4.1. Пара силы к данному центру (метод Пуансо)Скачать

5 Плоская система произвольно расположенных сил 5.1 Теорема Пуансо о параллельном переносе сил

5 ПЛОСКАЯ СИСТЕМА ПРОИЗВОЛЬНО РАСПОЛОЖЕННЫХ СИЛ

5.1 Теорема Пуансо о параллельном переносе сил

Теорема. Механическое состояние твердого тела не нарушится, если данную силу перенести параллельно первоначальному положению в произвольную точку тела, добавив при этом пару, момент которой равен моменту данной силы относительно новой точки приложения.

Для параллельного переноса силы Р из точки А в произвольную точку В, которая называется центром приведения, на основании аксиомы принципа отбрасывания системы сил эквивалентной нулю, необходимо добавить в точку В уравновешенную систему сил (Р*; Р**) (рисунок 5.1). При этом образуется пара сил (Р; Р**). В результате, полученная система трех сил рассматривается, как состоящая из силы Р*, приложенной в точке В и пары сил (Р; Р**) с моментом. Эту пару сил называют присоединенной, а ее плечо а равно плечу силы Р относительно точки В.

Таким образом, при приведении силы Р к точке, не лежащей на линии действия силы, получается эквивалентная система, состоящая из силы, равной по модулю и направлению силы Р и присоединенной пары сил, момент которой равен моменту данной силы относительно центра приведения.

5.2 Приведение к точке плоской системы произвольно

Приведением системы сил называется ее замена другой системой, эквивалентной первой, но более простой.

Теорема. Плоская система произвольно расположенных сил в общем случае эквивалентна одной силе, приложенной в центре приведения и одной паре.

Все силы системы переносятся в одну произвольно выбранную точку – точку приведения. Для этого используется теорема Пуансо. При любом переносе силы в точку, не лежащую на линии ее действия, добавляется пара сил.

Образовавшиеся при переносе пары называются присоединенными парами.

При заданной плоской системе произвольно расположенных сил (рисунок 5.2) все силы переносятся в одну точку О, получается пучок сил в данной точке, который можно заменить одной силой – главным вектором системы, а полученную систему заменяют одной эквивалентной парой – главным моментом системы.

(5.1)

Данная сила называется главным вектором системы.

Главный вектор плоской системы произвольно расположенных сил равен векторной сумме всех сил системы и приложен в центре приведения.

При проецировании всех сил системы на оси координат и, суммировании соответствующих проекций на эти оси, можно определить проекции главного вектора:

(5.2)

Графически главный вектор выражается замыкающей стороной силового многоугольника, который может быть построен на заданных силах. Аналитически модуль главного вектора можно вычислить по формуле с использованием величин проекций главного вектора:

(5.3)

Главный момент системы сил равен алгебраической сумме моментов сил системы относительно точки приведения.

(5.4)

Таким образом, произвольная плоская система сил приводится к одной силе – главному вектору системы сил и одному моменту – главному моменту системы сил.

5.3 Свойства главного вектора и главного момента

Свойства главного вектора и главного момента заключаются в следующем:

модуль и направление главного вектора данной системы не зависят от выбора центра приведения, так как силовой многоугольник, построенный на заданных силах при любом изменении положения точки приведения, будет один и тот же; величина и знак главного момента зависят от выбора центра приведения, так как при перемене точки приведения меняются плечи сил, модули остаются неизменными; главный вектор и равнодействующая системы сил векторно равны, но не эквивалентны (рисунок 5.3);

главный вектор и равнодействующая эквивалентны лишь в частном случае, когда главный момент системы равен нулю, то есть когда центр приведения находится на линии действия равнодействующей:

. (5.5)

Эта формула является математическим выражением теоремы о моменте равнодействующей, называемой теоремой Вариньона.

Теорема. Если равнодействующая плоской системы сил существует, то ее момент относительно любой точки равен алгебраической сумме моментов всех сил этой системы относительно той же точки.

Используя данную теорему можно определить точку на плоскости, относительно которой главный момент равен нулю. При этом условии произвольная плоская система сил может быть заменена одной силой, которая называется равнодействующей системы сил.

Численно, равнодействующая равна главному вектору системы сил, но приложена в другой точке, относительно которой главный момент равен нулю.

Численное значение равнодействующей определяется аналогично главному вектору системы сил, то есть из выражения:

(5.6)

Точку приложения равнодействующей можно найти по формуле:

(5.7)

где d – расстояние от выбранной точки приведения до точки приложения равнодействующей (рисунок 5.3);

Мгл – величина главного момента относительно выбранной точки приведения;

Ргл – величина главного вектора системы сил.

5.4 Различные случаи приведения плоской системы

произвольно расположенных сил

При использовании свойств главного вектора и главного момента можно предложить следующие случаи приведения плоской системы произвольно расположенных сил:

Ргл ? 0, Мгл ? 0, то есть главный вектор и главный момент не равны нулю – в этом случае система сил эквивалентна равнодействующей, которая равна по модулю главному вектору, параллельна ему и направлена в ту же сторону, но по другой линии действия; Ргл ? 0, Мгл = 0, в этом случае система эквивалентна равнодействующей, линия действия которой проходит через центр приведения и совпадает с главным вектором; Ргл = 0, Мгл ? 0, в этом случае система эквивалентна паре, так как модуль и направление главного вектора не зависят от выбора центра приведения; Ргл = 0, Мгл = 0, в этом случае система сил эквивалентна нулю, то есть находится в равновесии.

5.5 Аналитические условия равновесия плоской системы

произвольно расположенных сил

Плоская система произвольно расположенных сил находится в равновесии, когда главный вектор и главный момент равны нулю:

Ргл = 0; Мгл = 0. (5.8)

Таким образом, для равновесия плоской системы произвольно расположенных сил необходимо и достаточно, чтобы алгебраические суммы проекций всех сил на оси координат равнялись нулю, а также алгебраическая сумма моментов этих сил была равна нулю.

Условия равновесия упрощенно можно представить в виде равенств:

; ; . (5.9)

Условия равновесия плоской системы параллельных сил.

Для системы параллельных сил необходимо выбрать одну из осей проекций, параллельной этим силам, другую перпендикулярной им, в результате получим два уравнения равновесия данной системы сил (рисунок 5.4):

; . (5.10)

Итак, для равновесия плоской системы параллельных сил необходимо и достаточно, чтобы алгебраическая сумма всех сил равнялась нулю, и алгебраическая сумма моментов всех сил относительно любой точки плоскости также равнялась нулю.

При решении задач на равновесие произвольной плоской системы сил можно найти три неизвестных, а при рассмотрении равновесия плоской системы параллельных сил – не более двух. Если количество неизвестных превышает число уравнений статики, то задача становится статически неопределимой.

При решении задач статики аналитическим способом целесообразно составлять уравнения равновесия так, чтобы в каждом из них была только одна неизвестная величина, для этого достаточно рационально подбирать расположение осей координат и центры моментов.