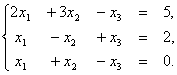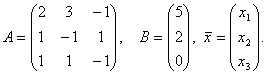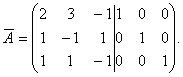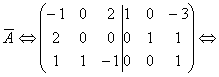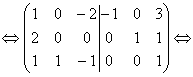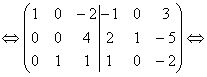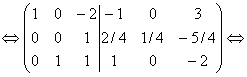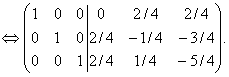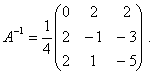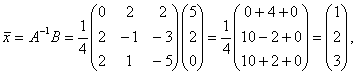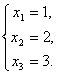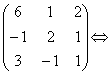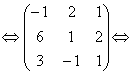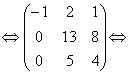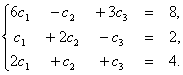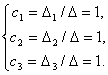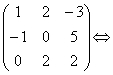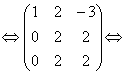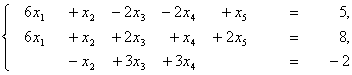Пример №1 . Даны векторы ε1(2;1;3), ε2(3;-2;1), ε3(1;-3;-4), X(7;0;7). Показать, что векторы образуют базис трехмерного пространства и найти координаты вектора X в этом базисе.
Решение. Данная задача состоит из двух частей. Сначала необходимо проверить, образуют ли векторы базис. Векторы образуют базис, если определитель, составленный из координат этих векторов, отличен от нуля, в противном случае вектора не являются базисными и вектор X нельзя разложить по данному базису.
Вычислим определитель матрицы:
| E = |
|
∆ = 2*((-2)*(-4) — (-3)*1) — 3*(1*(-4) — (-3)*3) + 1*(1*1 — (-2)*3) = 14
Определитель матрицы равен ∆ =14
Так как определитель отличен от нуля, то векторы образуют базис, следовательно, вектор X можно разложить по данному базису. Т.е. существуют такие числа α1α2α3, что имеет место равенство:
X = ⓫ε1 + ⓬ε2 + ⓭ε3
Запишем данное равенство в координатной форме:
(7;0;7) = α(2;1;3) + α(3;-2;1) + α(1;-3;-4)
Используя свойства векторов, получим следующее равенство:
(7;0;7) = (2α1;1α1;3α1😉 + (3α2;-2α2;1α2😉 + (1α3;-3α3;-4α3😉
(7;0;7) = (2α1 + 3α2 + 1α3;1α1 -2α2 -3α3;3α1 + 1α2 -4α3)
По свойству равенства векторов имеем:
2α1 + 3α2 + 1α3 = 7
1α1 -2α2 -3α3 = 0
3α1 + 1α2 -4α3 = 7
Решаем полученную систему уравнений методом Гаусса или методом Крамера.
Ответ:
| X = |
|
X = 2ε1 + ε2
В системе векторов a1, a2, a3, a4 найти любую подсистему векторов, которые образуют базис, разложить векторы по базису, перейти к другому базису, найти коэффициенты разложения векторов во втором базисе; в обоих случаях определить обратные матрицы, соответствующие векторам базиса. Правильность вычисления в каждом случае проверить с помощью умножения вектора слева на матрицу, обратную матрице вектора базиса.
Пример №2 . В системе векторов a1, a2, a3, a4 найти любую подсистему векторов, которые образуют базис, разложить векторы по базису, перейти к другому базису, найти коэффициенты разложения векторов во втором базисе; в обоих случаях определить обратные матрицы, соответствующие векторам базиса. Правильность вычисления в каждом случае проверить с помощью умножения вектора слева на матрицу, обратную матрице вектора базиса.
a1=(1;5;3), a2=(2;1;-1), a3=(4;2;1), a4=(17;13;4).
Видео:Координаты в новом базисеСкачать

Координаты и преобразования координат в линейном пространстве
Видео:Доказать, что векторы a, b, c образуют базис и найти координаты вектора d в этом базисеСкачать

Координаты векторов в данном базисе линейного пространства
Пусть — базис линейного пространства . Каждый вектор можно разложить по базису (см. теорему 8.1), т.е. представить в виде , причем коэффициенты в разложении определяются однозначно. Эти коэффициенты называются координатами вектора в базисе (или относительно базиса ). Координаты вектора — это упорядоченный на бор чисел, который представляется в виде матрицы-столбца и называется координатным столбцом вектора (в данном базисе). Вектор и его координатный столбец обозначаются одной и той же буквой полужирной или светлой соответственно.
Если базис (как упорядоченный набор векторов) представить в виде символической матрицы-строки , то разложение вектора по базису можно записать следующим образом:
Здесь умножение символической матрицы-строки на числовую матрицу-столбец производится по правилам умножения матриц.
При необходимости, если речь идет о разных базисах, у координатного столбца указывается обозначение базиса, относительно которого получены координаты, например, — координатный столбец вектора в базисе .
Из теоремы 8.1 следует, что равные векторы имеют равные соответствующие координаты (в одном и том же базисе), и наоборот, если координаты векторов (в одном и том же базисе) соответственно равны, то равны и сами векторы .
Видео:Матрица переходаСкачать
Линейные операции в координатной форме
Пусть — базис линейного пространства , векторы и имеют в этом базисе координаты и соответственно, т.е.
Складывая эти равенства, получаем .
т.е. при сложении векторов их координаты складываются .
Умножая второе равенство в (8.7) на число , получаем
т.е. при умножении вектора на число все его координаты умножаются на это число .
Другими словами, сумма векторов имеет координаты , а произведение имеет координаты . Разумеется, что все координаты получены в одном базисе .
1. Нетрудно показать, что координатный столбец линейной комбинации векторов равен линейной комбинации координатных столбцов этих векторов.
2. Если система векторов линейно зависима (линейно независима), то их координатные столбцы, полученные относительно одного базиса, образуют линейно зависимую (соответственно, линейно независимую) систему. Это следует из равносильности равенств и . Например, если в этих равенствах не все коэффициенты равны нулю, т.е. система векторов и система их координатных столбцов линейно зависимы одновременно.
3. Все свойства линейной зависимости и линейной независимости векторов переносятся без изменений на их координатные столбцы, полученные в одном и том же базисе. И наоборот, свойства для матриц-столбцов, переносятся на векторы, если матрицы-столбцы считать их координатными столбцами.
4. Выбрав в n-мерном вещественном линейном пространстве некоторый базис, можно установить взаимно однозначное соответствие: каждому вектору поставить в соответствие его координатный столбец (в вы бранном базисе), и наоборот, каждому координатному столбцу поставить в соответствие вектор. Другими словами, любой фиксированный базис n-мерного вещественного линейного пространства позволяет установить взаимно однозначное соответствие между всеми векторами вещественно го пространства и всеми столбцами n-мерного арифметического пространства . Это соответствие обозначается . Для n-мерного комплексного линейного пространства аналогичное взаимно однозначное соответствие устанавливается с пространством .
Видео:Базис и матрица перехода. Координаты вектора в разных базисах.Скачать

Преобразование координат вектора при замене базиса
Пусть заданы два базиса пространства и . Базис будем условно называть «старым», а базис — «новым». Пусть известны разложения каждого вектора нового базиса по старому базису:
Записывая по столбцам координаты векторов в базисе , составляем матрицу:
Квадратная матрица , составленная из координатных столбцов векторов нового базиса в старом базисе , называется матрицей перехода от старого базиса к новому. При помощи матрицы перехода (8.9) формулы (8.8) можно записать в виде:
Умножение символической матрицы-строки на матрицу перехода в (8.10) производится по правилам умножения матриц.
Пусть в базисе вектор имеет координаты , а в базисе — координаты , т.е.
Подставляя в правую часть последнего равенства выражение (8.10), получаем — два разложения вектора в одном и том же базисе . Коэффициенты этих разложений должны совпадать (по теореме 8.1), так как это координаты одного и того же вектора в одном базисе. Поэтому
Формула (8.11) устанавливает связь координат вектора в разных базисах: координатный столбец вектора в старом базисе получается в результате умножения матрицы перехода на координатный столбец вектора в новом базисе .
Пример 8.3. В пространстве многочленов степени не выше второй даны две системы многочленов:
Доказать, что каждая система является базисом пространства . Найти матрицу перехода от базиса к базису . Определить координаты квадратного трехчлена относительно базисов и .
Решение. Система многочленов является стандартным базисом пространства . Докажем, что система является базисом. По ступим следующим образом. Найдем координатные столбцы этих многочленов в стандартном базисе. Раскладывая по базису , получаем
Составим из этих столбцов матрицу . Ранг этой матрицы равен 3, так как . Следовательно, столбцы линейно независимы, тогда и многочлены линейно независимы (см. пункт 2 замечаний 8.5). Итак, многочлены являются базисом пространства , а матрица — искомая матрица перехода от базиса к базису . Осталось найти координаты многочлена в этих базисах. Раскладывая по базисам, находим
Проверим результат, вычисляя по формуле (8.11):
Видео:Как разложить вектор по базису - bezbotvyСкачать

Свойства матрицы перехода от одного базиса к другому
1. Пусть имеются три базиса пространства и известны матрицы перехода: от базиса к базису ; от к ; от к . Тогда
Действительно, запишем связь (8.10) для данных базисов:
Подставляя первое выражение во второе равенство, получаем . Сравнивая с третьим равенством, приходим к (8.12).
2. Если — матрица перехода от базиса к базису , то матрица обратима и обратная матрица является матрицей перехода от базиса к базису . Координаты вектора в базисах и связаны формулами:
В самом деле, пусть — матрица перехода от базиса к базису . Учитывая, что матрица перехода от базиса к базису — единичная, применяем свойство 1 к трем базисам . Для трех базисов аналогично получаем: . Следовательно, .
3. Всякая обратимая квадратная матрица n-го порядка может служить матрицей перехода от одного базиса n-мерного линейного пространства к другому базису.
Пример 8.4. В двумерном арифметическом пространстве даны два базиса: и . Найти матрицу перехода от базиса к базису и координаты вектора в каждом из базисов.
Решение. Рассмотрим стандартный базис пространства . Находим координаты векторов в стандартном базисе. Раскладываем вектор
В стандартном базисе пространства координатный столбец совпадает с вектором . Для других векторов аналогично получаем . Из координатных столбцов составим матрицы перехода (8.9) от стандартного базиса к данным базисам и
По свойству 1 матриц перехода имеем . .По свойству 2: . Поэтому
В стандартном базисе пространства координатный столбец совпадает с вектором . Найдем координаты этого вектора в базисе (по свойству 2 матрицы перехода):
В самом деле, справедливо разложение
Найдем координаты вектора в базисе двумя способами
Полученный результат подтверждает разложение:
Видео:Матрицы и векторыСкачать

Координаты вектора из матрицы
Задача 1 . Решить систему уравнений с помощью обратной матрицы.
Решение. Запишем систему в матричной форме 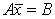
Найдем обратную матрицу к матрице А. Составим расширенную матрицу и с помощью элементарных преобразований приведем ее левую часть к единичной матрице.
Возьмем третью строку. Сложим ее со второй строкой и сложим с первой строкой, умножив на (-3).
умножим первую строку на (-1):
возьмем первую строку. Умножим ее на (-2), сложим со второй строкой и сложим с третьей строкой, умножив первую строку на (-1):
разделим вторую строку на (4)
возьмем вторую строку. Умножим ее на 2 и сложим с первой строкой и сложим с третьей строкой, умножив вторую строку на (-1):
переставим две последние строки:
В левой части расширенной матрицы получена единичная матрица, следовательно, в правой части получена обратная матрица.
Найдем решение системы.
Задача 2 . Даны две системы векторов:
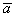
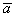
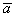
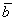
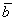
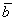
Найти ранги данных систем и выяснить, какая из них образует базис. Найти координаты вектора 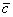
Решение. Составим матрицу из координат векторов первой системы и найдем ее ранг. Для этого приведем ее к треугольному виду.
переставим первые две строки
умножим первую строку на 6 и сложим со второй, умножим первую строку на 3 и сложим с третьей строкой
разделим вторую строку на 13
умножим вторую строку на (-5) и сложим с третьей
Ранг системы векторов равен 3. Векторы линейно независимы и поскольку их три и они трехмерные, то они образуют базис в трехмерном пространстве. Любой вектор пространства можно разложить по векторам этой системы.
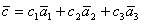
Найдем координаты разложения. Подставим координаты векторов в последнее равенство.
Так как векторы равны, то равны их координаты.
Получена система трех линейных уравнений с тремя неизвестными. Решим ее методом Крамера. Найдем главный определитель системы.
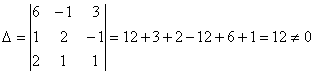
Система имеет единственное решение. Найдем вспомогательные определители. Они получаются из главного определителя заменой соответствующего столбца на столбец свободных членов.
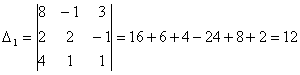
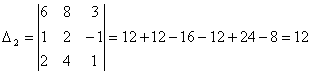
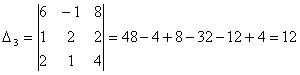
Выпишем решение системы.
Разложение вектора 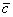
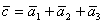
Найдем ранг второй системы векторов. Составим матрицу из координат векторов и приведем ее к треугольному виду.
прибавим первую строку ко второй
умножим вторую строку на (-1) и сложим с третьей
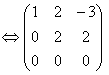
Ранг системы векторов равен 2. Векторы линейно зависимы и они не образуют базиса в трехмерном пространстве.
и сделать переход к другому неотрицательному базисному решению. Выписать общее решение системы.
Решение. 1. Заполняем исходную таблицу. Умножаем третье уравнение на (-1).
📺 Видео
Координаты вектора. 9 класс.Скачать

Высшая математика. Линейные пространства. Векторы. БазисСкачать

Самый короткий тест на интеллект Задача Массачусетского профессораСкачать

Улучшить видео. Нейросеть Topaz Video AIСкачать

Математика это не ИсламСкачать

Разложение вектора по базису. 9 класс.Скачать

Собственные векторы и собственные значения матрицыСкачать

Линейная алгебра. Векторы и операции над векторами.Скачать

5 4 Координаты Преобразование координат при замене базисаСкачать

Координаты вектора в пространстве. 11 класс.Скачать

9 класс, 4 урок, Простейшие задачи в координатахСкачать

Замена базиса. ТемаСкачать

18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать

Нахождение координат вектора. Практическая часть. 9 класс.Скачать