Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
- «Управление общеобразовательной организацией: новые тенденции и современные технологии»
- Дистанционное обучение как современный формат преподавания
- Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
- Математика: теория и методика преподавания в образовательной организации
- Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
- Дистанционные курсы для педагогов
- Другие материалы
- Вам будут интересны эти курсы:
- Оставьте свой комментарий
- Автор материала
- Дистанционные курсы для педагогов
- Подарочные сертификаты
- Контрольная работа № 1 по теме «Координаты и векторы в пространстве» (11 класс, Мерзляк А.Г. и др.)
- Просмотр содержимого документа «Контрольная работа № 1 по теме «Координаты и векторы в пространстве» (11 класс, Мерзляк А.Г. и др.)»
- Декартовы координаты и векторы в пространстве тренажёр по геометрии (10 класс) по теме
- Скачать:
- Предварительный просмотр:
- Предварительный просмотр:
- 🔥 Видео
Видео:ДЕКАРТОВЫ КООРДИНАТЫ. Контрольная № 3 Геометрия 9 класс.Скачать

«Управление общеобразовательной организацией:
новые тенденции и современные технологии»
Свидетельство и скидка на обучение каждому участнику
Контрольная работа по теме «Декартовы координаты и векторы в пространстве»
Даны точки А(2;-1;0) и В(-4;2;2). Найдите координаты середины отрезка АВ и длину отрезка АВ.
Даны координаты точек А(1;-1;-4), В(-3;-1;0), С(-1;2;5), Д(2;-3;1). Найдите косинус угла между векторами и
При каком значении т векторы и перпендикулярны, если .
Даны точки А(-1;4;3) и В(5;-2;0). Найдите координаты середины отрезка АВ и длину отрезка АВ.
Даны координаты точек А(3;-2;1), В(-1;2;1), С(2;-3;5), Д(-1;-1;-2). Найдите косинус угла между векторами и
При каком значении т векторы и перпендикулярны, если .
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
- Сейчас обучается 935 человек из 80 регионов
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
- Сейчас обучается 316 человек из 70 регионов
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
- Сейчас обучается 696 человек из 75 регионов
Ищем педагогов в команду «Инфоурок»
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
5 478 159 материалов в базе
Видео:Векторы. Метод координат. Вебинар | МатематикаСкачать

Дистанционные курсы для педагогов
Другие материалы
- 09.02.2018
- 418
- 09.02.2018
- 4483
- 09.02.2018
- 2128
- 09.02.2018
- 3361
- 09.02.2018
- 292
- 09.02.2018
- 503
- 09.02.2018
- 1018
- 09.02.2018
- 640
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Добавить в избранное
- 09.02.2018 2134 —> —> —> —>
- DOCX 26.1 кбайт —> —>
- Рейтинг: 5 из 5
- Оцените материал:
Настоящий материал опубликован пользователем Лебедева Светлана Александровна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
Автор материала
- На проекте: 8 лет и 1 месяц
- Подписчики: 5
- Всего просмотров: 11897
- Всего материалов: 16
Московский институт профессиональной
переподготовки и повышения
квалификации педагогов
Видео:Координаты вектора. 9 класс.Скачать

Дистанционные курсы
для педагогов
548 курсов от 690 рублей
Выбрать курс со скидкой
Выдаём документы
установленного образца!
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
В России утвердили новые правила аккредитации образовательных учреждений
Время чтения: 1 минута
В Роспотребнадзоре заявили о широком распространении COVID-19 среди детей
Время чтения: 1 минута
В России ежегодно будут обучать плаванию не менее 500 тыс. детей
Время чтения: 2 минуты
Проходной балл ЕГЭ для поступления на бюджет снизился впервые за 10 лет
Время чтения: 3 минуты
Стоимость обучения на первом курсе в вузах РФ за год выросла на 10%
Время чтения: 3 минуты
В Якутске все классы, кроме девятых и одиннадцатых, перейдут на удаленку
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Видео:Прямоугольная система координат в пространстве. 11 класс.Скачать

Контрольная работа № 1 по теме «Координаты и векторы в пространстве» (11 класс, Мерзляк А.Г. и др.)
Даны четыре варианта контрольной работы, удобно вносить изменения и печатать.
Просмотр содержимого документа
«Контрольная работа № 1 по теме «Координаты и векторы в пространстве» (11 класс, Мерзляк А.Г. и др.)»
Контрольная работа № 1 по теме «Координаты и векторы в пространстве»
1. Точка A — середина отрезка MK. Найдите координаты точки A и длину отрезка MK, если M (5; −2; 1), K (3; 4; −3).
2. Точки A и B симметричны относительно точки C. Найдите координаты точки B, если A (−3; 5; −7), C (6; 2; −1).
3. Даны векторы 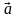
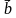
1) координаты вектора 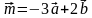
2) косинус угла между векторами 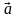
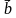
4. Даны векторы 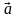
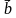
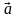
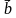
5. Составьте уравнение плоскости, проходящей через точку A и перпендикулярной прямой AB, если A (1; 2; −3), B (4; 8; −6).
6. Дан куб ABCDA1B1C1D1, ребро которого равно 1 см. На диагонали C1D его грани отметили точку M так, что DM : MC1 = 5 : 3.
1) Выразите вектор 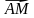
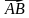
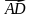
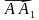
2) Найдите модуль вектора 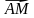
1. Точка M — середина отрезка AB. Найдите координаты точки M и длину отрезка AB, если A (6; −5; 2), B (−4; 3; 10).
2. Точки M и K симметричны относительно точки D. Найдите координаты точки K, если M (4; −6; 3), D (−2; 1; 5).
3. Даны векторы 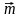
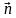
1) координаты вектора 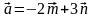
2) косинус угла между векторами 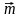
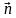
4. Даны векторы 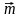
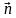
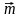
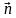
5. Составьте уравнение плоскости, проходящей через точку B и перпендикулярной прямой BC, если B (3; −2; 4), C (−2; 8; 19).
6. Дан куб ABCDA1B1C1D1, ребро которого равно 1 см. На диагонали AD1 его грани отметили точку E так, что AE : ED1 = 2 : 7.
1) Выразите вектор 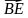
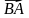
2) Найдите модуль вектора 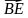
1. Точка K — середина отрезка CD. Найдите координаты точки K и длину отрезка CD, если C (−3; 4; −1), D (1; −2; 3).
2. Точки E и F симметричны относительно точки P. Найдите координаты точки F, если E (0; −8; 4), P (−4; 2; 2).
3. Даны векторы 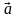
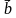
1) координаты вектора ;
2) косинус угла между векторами 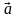
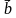
4. Даны векторы 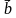
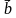
5. Составьте уравнение плоскости, проходящей через точку C и перпендикулярной прямой CD, если C (4; 1; −1), D (7; −2; 5).
6. Дан куб ABCDA1B1C1D1, ребро которого равно 1 см. На диагонали A1B его грани отметили точку K так, что A1K : KB = 4 : 3.
1) Выразите вектор через векторы , и .
2) Найдите модуль вектора .
1. Точка D — середина отрезка FK. Найдите координаты точки D и длину отрезка FK, если F (6; −3; 2), K (4; 1; 4).
2. Точки B и C симметричны относительно точки M. Найдите координаты точки B, если C (9; −5; 6), M (3; 0; −2).
3. Даны векторы 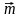
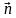
1) координаты вектора ;
2) косинус угла между векторами 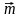
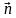
4. Даны векторы 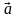
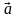
5. Составьте уравнение плоскости, проходящей через точку D и перпендикулярной прямой DM, если D (−3; 20; −4), M (9; 24; 16).
6. Дан куб ABCDA1B1C1D1, ребро которого равно 1 см. На диагонали AC его грани отметили точку F так, что AF : FC = 3 : 7.
Видео:Подготовка к контрольной работе Координаты и векторыСкачать

Декартовы координаты и векторы в пространстве
тренажёр по геометрии (10 класс) по теме
Материал содержит тест и контрольную работу по теме: «Декартовы координаты и векторы в пространстве»
Видео:Контрольная работа по геометрии по теме "Метод координат". Разбор заданий. Геометрия 9 классСкачать

Скачать:
| Вложение | Размер |
|---|---|
| kontrolnaya_rabota.docx | 12.62 КБ |
| test.docx | 43.43 КБ |
Видео:Координаты вектора в пространстве. 11 класс.Скачать

Предварительный просмотр:
Контрольная работа по теме:
«Координаты и векторы в пространстве»
Изобразите на рисунке векторы, равные:
а(-1;2;3) и b(5;х;-1). При каких значениях х векторы а и b перпендикулярны?
а(3;-5;2) и b(0;7;-1). Найдите координаты вектора .
4. Даны координаты точек
А(1;-1;-4), В(-3;-1;0, С(-1;2;5), D(2;-3;1). Найдите косинус угла между векторами .
5. Найдите периметр треугольника с вершинами
6. Напишите уравнение плоскости, проходящей через середину отрезка АВ перпендикулярно к нему , если А (3,-4,7) и В (1,0,-1).
Видео:Координаты точки и координаты вектора 1.Скачать

Предварительный просмотр:
Тест по теме «Векторы в пространстве»
1. Какое из следующих утверждений неверно?
а) длиной ненулевого вектора называется длина отрезка АВ;
б) нулевой вектор считается сонаправленным любому вектору;
в) ;
г) разностью векторов а и b называется такой вектор. сумма которого с вектором b равна вектору а;
д) векторы называются равными, если равны их длины.
2. Упростите выражение:
, если ABCDA ₁ B ₁ C ₁ D ₁ — параллелепипед.
3. Какое из следующих утверждений верно?
а) сумма нескольких векторов зависит от того, в каком порядке они складываются;
б) противоположные векторы равны;
в) для нахождения разности векторов необходимо, чтобы они выходили из одной точки;
г) произведение вектора на число является число;
д) для любых векторов а и b не выполняется равенство а+b=b+a.
4. Ребро куба ABCDA ₁ B ₁ C ₁ D ₁ равно 1. Найдите | |.
а) 1; б) 2; в) ; г) ; д) 0,5 .
5. Какое из следующих утверждений неверно?
а) векторы называются компланарными, если при откладывании их от одной и той же точки они будут лежать в одной плоскости;
б) если вектор с можно разложить по векторам а и b, т.е. представить в виде с=ха+yb, где х, y- некоторые числа, то векторы а, b, c компланарны;
в) для сложения трёх некомпланарных векторов используют правило параллелепипеда;
г) любые два вектора компланарны;
д) любые три вектора некомпланарны.
6. Известно, что . Тогда прямые АС и ВD:
а) параллельны; б) пересекаются; в) скрещиваются; г) совпадают;
д) выполняются все условия пунктов а-г.
7. Векторы p, a, b некомпланарны, если:
а) при откладывании из одной точки они не лежат в одной плоскости;
б) два из данных векторов коллинеарны; в) один из данных векторов нулевой;
8. ABCDA ₁ B ₁ C ₁ D ₁ -параллелепипед. Какой из предложенных векторов будет компланарен с векторами и ?
9.Известно, что 2 = , тогда векторы , являются:
а) некомпланарными; б) сонаправленными; в) коллинеарными;
г) нулевыми; д) компланарными.
10. Даны параллелограммы ABCD и AB ₁ C ₁ D ₁ . Тогда векторы , , :
а) нулевые; б) равные; в) противоположные; г) компланарные; д) некомпланарные.
🔥 Видео
11 класс, 1 урок, Прямоугольная система координат в пространствеСкачать

18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать

Декартовы координаты и векторы в пространствеСкачать
Геометрия 11 класс (Урок№1 - Координаты в пространстве. Система координат.)Скачать

9 класс, 3 урок, Связь между координатами вектора и координатами его начала и концаСкачать

РАЗБОР КОНТРОЛЬНОЙ РАБОТЫ | 9 КЛАСС ГЕОМЕТРИЯ АТАНАСЯН | ВЕКТОРЫСкачать

Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Урок 8. Векторные величины. Действия над векторами.Скачать

Прямоугольная система координат в пространстве. Практическая часть. 11 класс.Скачать

Видеоурок "Преобразование координат"Скачать

Полярная система координатСкачать

ВЕКТОРЫ. Контрольная № 4 Геометрия 9 класс.Скачать





